BQ法边坡工程岩体质量指标计算的修正系数研究

， ，，

(1.宏大国源(芜湖)资源环境治理有限公司，安徽 芜湖 241200；2.宏大爆破有限公司，广州 510623)

1 研究背景

边坡工程岩体质量分级是在以往工程实践经验和大量岩石力学试验基础上，配合少量简易的地质勘察和室内、现场试验，通过比较确定的量化经验公式计算出工程岩体质量等级。准确的分级能反映工程岩体的固有属性，为评价边坡稳定性、选取岩体力学参数和设计加固方案提供重要依据。

回顾整个边坡岩体分级的发展过程，按照其来源可将边坡岩体分级方法归为2个大类：第1类为源于边坡的岩体分级方法，如国外的边坡稳定概率分级 SSPC[1-3]和自然边坡分级NSM[4]，以及国内的定性分级——建筑边坡工程规范岩质边坡岩体分类[5]和水利水电工程边坡设计规范边坡岩体分类[6]等；第2类为源于地下工程的岩体分级方法，如Bieniawski[7-8]提出的RMR、《工程岩体分级标准》(GB/T 50218—2014)(以下简称《国标》)中的BQ法[9]，在这类边坡岩体分级方法中大部分是在RMR基础上经过修正后建立的，如SMR[10-11]、水利水电工程边坡岩体分级CSMR[12]、西南山区高等级公路边坡岩体分级HSMR[13]、天山公路边坡岩体分级TSMR[14]以及适用于边坡岩体稳定性评价的GSMR[15]等。在2015年发布的最新《国标》[9]中给出了基于BQ法的边坡工程岩体质量指标修正值[BQ](以下简称边坡[BQ])，已经初步应用于边坡工程岩体分级和边坡自稳能力评估。

通过对边坡岩体分级的现状研究可知：在第1类边坡岩体分级方法中，来自国外的SSPC和NSM具有较强的地区针对性，并不适合我国边坡岩体分级[16]；而国内的方法则以边坡岩体的定性分级为主，无法给出定量的分级指标，因此容易受主观性思维的影响，且对研究人员的专业知识和工程经验要求较高。以上这些因素造成了第1类方法未能在国内的边坡岩体分级中得到广泛的应用。相比之下，第2类边坡岩体分级法在各岩体行业的边坡工程中应用广泛，且随着工程的发展不断地更新完善。

《国标》BQ法在其制定过程中，综合参考国内外岩体质量分级方法，同时紧密结合我国岩体工程特征，通过少量的岩石试验和简单的数学计算获得工程岩体基本质量指标BQ，再根据岩体的工程性质进行修正，通过岩体质量指标修正值[BQ]确定工程岩体级别。BQ法采用的是定性和定量相结合的方法，具有较强的科学性和实用性，推广至今，已在各岩体行业得到广泛应用，为工程建设提供了必要依据，并取得了较高的认可[17-18]。

《国标》BQ法最初发布的时间为1994年，但当时的分级标准仅给出了地下工程岩体质量指标修正值[BQ] (以下简称地下[BQ])的计算公式，未涉及边坡[BQ]的计算，因此基于BQ法的边坡岩体分级法的研究和发展落后于基于RMR法的各种边坡岩体分级法。为了满足工程和研究的需要，2015年发布的《国标》中给出了边坡[BQ]计算公式，填补了这一方面的空白。为了使BQ法能更好地用于边坡工程岩体质量分级及其他与边坡工程相关的研究工作，有必要对边坡[BQ]计算公式进行研究和完善。

本文通过对《国标》中边坡[BQ]计算公式的研究，指出了边坡[BQ]计算公式中的修正项和修正系数评价指标存在改进和完善的空间。因此，在现有的边坡[BQ]计算公式的基础上，补充了坡高影响修正系数和应力状态影响修正系数以及相应的计算公式和取值标准，在结构面性状影响修正上细化了评价指标和取值标准，给出了优化后的边坡[BQ]计算公式和BQ法边坡稳定性评价系统。

2 基于BQ法的边坡岩体分级研究

大多数工程岩体分级方法是以岩石强度和岩体完整性作为其基本要素，在此基础上再考虑其他的因素进行修正[19]，BQ法也参考了这种模式，采用两步分级法：第1步，按岩体的基本质量指标BQ进行初步分级，岩体的基本质量由岩石坚硬程度和岩体完整程度来衡量，以岩石饱和单轴抗压强度来划分岩石的坚硬程度，而岩体的完整程度则采用岩体完整性指数来表示；第2步，针对各类工程岩体的特点，考虑其他因素(地下水、应力状态和结构面等)对岩体质量的影响，对BQ进行修正，按修正后所得的[BQ]进行再次分级。《国标》中的边坡[BQ]计算考虑了结构面产状、类型、延伸性以及地下水的影响，并在计算公式中给出了相应的修正系数。

边坡[BQ]计算公式在计算形式上参考了《国标》中的地下[BQ]计算公式，在结构面影响修正上参考了CSMR和SMR的修正方法，上述3种岩体分级方法均已得到了较为广泛的应用和认可，因此，边坡[BQ]的计算结果具有合理性和实用性。但经过分析发现，其计算公式仍有少许改进和完善的空间：

(1)边坡[BQ]的计算中缺少坡高修正，《国标》中也指出边坡[BQ]只能直接用于高度≤60 m的边坡，而对于高度>60 m的边坡需要结合工程进行专门论证。但现实工程中存在许多高度>60 m的边坡(如水利水电边坡和矿山边坡)，这些边坡的工程岩体质量等级则难以通过现有的边坡[BQ]计算公式直接给出，增加了工作量和应用难度。

(2)边坡[BQ]缺少应力状态影响修正，因此只适用于地势平缓、应力水平较低的边坡岩体分级，而对于那些开挖程度深且处在高地应力区的高陡边坡，应力状态对岩体质量的影响是不能忽略的。

(3)边坡[BQ]在进行结构面影响修正时涉及到了结构面类型与延伸性，缺少结构面的其他主要性状，如结构面的张开度、风化程度、起伏粗糙状况和填充物情况等。即使在结构面类型与延伸性相同的条件下，结构面也会因为上述主要性状的差异，而对岩体质量产生不同程度的影响。

本文针对上述3点，补充了必要的修正系数，细化了评价指标和取值标准，给出了优化后的边坡[BQ]计算公式和BQ法边坡稳定性评价系统。

3 坡高影响修正系数

3.1 等效指标比

BQ法和RMR法在国内具有广泛的研究和应用，2种分级法都将岩体划分成5个等级,其中RMR法的每个等级可进一步划分出2个亚级，见表1，且在岩体等级上存在一定的对应关系。因此，人们常常同时用这2种方法对工程岩体进行分级，再将2种分级结果进行对比分析，给出综合性的岩体等级。

表1 RMR岩体分级标准Table 1 RMR rock mass classification criterion

在岩体分级的研究过程中，许多学者[20-25]将BQ和RMR绘在同一坐标系中，尝试用不同类型的曲线进行拟合，建立了单个或多个工程条件下BQ和RMR之间的函数关系式，其中采用最多的是线性拟合。通过查阅相关文献[26-31]可知，以RMR为x轴，BQ为y轴，按照y=kx+b拟合出的函数式会出现b>0和b<0这2种情况。本文将b>0的称为第1类函数式，b<0的称为第2类函数式。在第1类和第2类函数式中分别选取6个拟合相关系数较高的函数式来进行分析，具体函数式见表2。

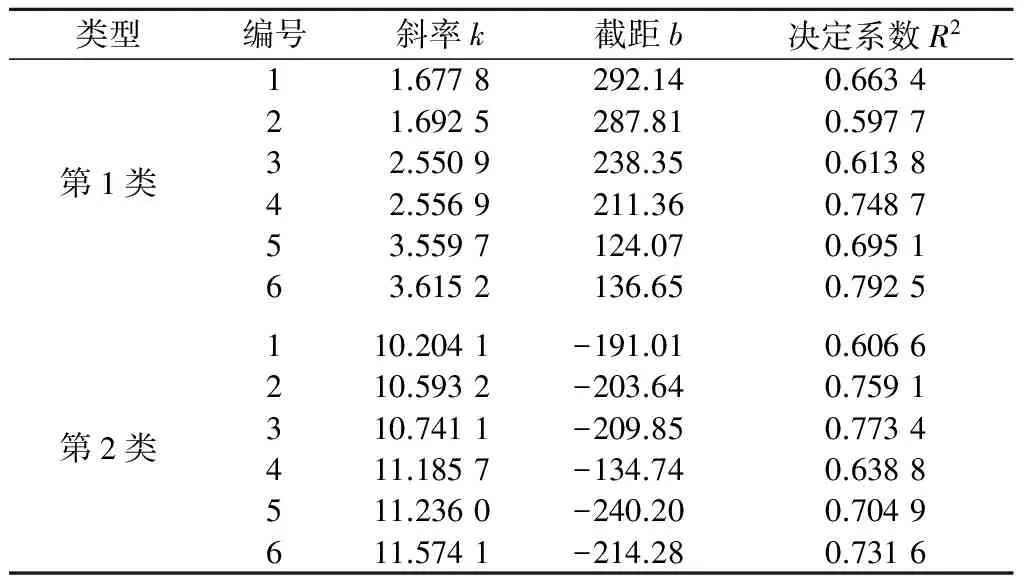
表2 RMR-BQ线性函数关系式Table 2 RMR-BQ linear functional relation

为了研究RMR和BQ之间的等效线性关系，本文通过“平均函数式”来等效替代同一类型的函数式。求取“平均函数式”的方法是对同一类型函数式中对应的各常数项求平均值，计算式为

(1)

将表2中所列数据代入式(1)，可分别得出第1类和第2类函数式的“平均函数式”：

y=2.608 8x+215.06 ；

(2)

y=10.922 4x-198.95 。

(3)

联立式(2)和式(3)可得

y/x=BQ/RMR=344.98/49.80=6.927 3 。

(4)

RMR法和BQ法的岩体分级都是按5个等级来划分，《国标》中指出RMR与BQ的各级别界限划分值具有较好的对应关系，对相同岩体进行分级时，BQ法可能比RMR法保守半级至1/4级。根据表1可知，式(4)中RMR值对应的岩体等级为Ⅲ级，且位于等级区间的中部；根据《国标》中的工程岩体基本质量分级表可知，式(4)中BQ值对应的岩体等级为Ⅳ级，且非常接近Ⅲ级的下限。由此可见，式(4)中BQ比RMR对应的岩体等级恰好保守半级左右，与《国标》中的结论较为一致。

将表2中2种类型的函数式和式(4)绘在同一坐标系内，如图1所示。

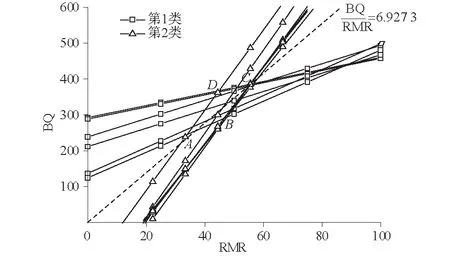
图1 RMR与BQ之间的函数关系Fig.1 Functional relationship between RMR and BQ

第1类函数的6条曲线和第2类函数的6条曲线分别组成了2个相交的条带状区域，相交部分为一个近似于平行四边形的狭小区域ABCD，而式(4)所对应的曲线几乎与对角线AC重合。将2个条带状区域视为一个整体区域，式(4) 所对应的曲线则恰好位于整体区域的中部，从整体上综合反映了BQ随着RMR变化的趋势，可看作RMR和BQ之间的等效线性关系。引入与RMR和BQ相关的常量ke，其定义式为

(5)

式中(RMR)e和(BQ)e分别为RMR和BQ的等效指标，是RMR和BQ在不同工程和地质条件下所取的等效均值，与收集整理的RMR-BQ线性函数式的来源、数量和离散程度等因素有关。等效指标(BQ)e和(RMR)e的比值ke称为等效指标比，反映了在线性拟合条件下，BQ和RMR之间的等效线性关系。由式(5)可知，根据本文搜集整理的RMR-BQ线性函数式所算出的(BQ)e=344.98，(RMR)e=49.80，ke=6.927 3。ke作为常量可以很方便地用于RMR和BQ之间的换算。

3.2 坡高影响修正系数的计算公式

边坡的稳定性与坡高关系密切，在岩层倾角、结构面抗剪强度不变的情况下，边坡稳定性随边坡高度的增大而减小。而边坡岩体等级在一定程度上也反映了边坡的稳定性情况，因此有必要在边坡岩体质量分级中补充坡高对岩体质量等级的影响。

CSMR分类体系[12]是RMR-SMR系统的一种应用，它是在RMR-SMR体系的基础上，引入坡高影响修正系数和结构面条件修正系数，提出的一种用于边坡岩体质量评价的方法，其具体表达式为

CSMR=ξrRMR-λF1F2F3+F4。

(6)

式中：ξr为坡高影响修正系数；λ为结构面条件修正系数，和《国标》中边坡[BQ]计算公式中的λ含义相近；F1，F2，F3为结构面产状调整值，和《国标》中边坡[BQ]计算公式中的K5含义相近；F4是与边坡开挖方式有关的修正系数。

令RMR经过坡高修正后为(RMR)h，根据CSMR分类体系中给出的ξr的计算公式可得

(7)

式中：H为坡高；Hr为参考坡高，在CSMR分类体系中Hr=80 m。Hr的含义在于当H=Hr时，RMR无需进行坡高修正，即ξr=1，因此式(7)又可写作

(8)

之前设定，在式(2)和式(3)中x=RMR，y=BQ。由BQ公式易知BQ≥100，代入式(2)和式(3)可得：

BQ=2.608 8RMR+215.06≥100 ；

(9)

BQ=10.922 4RMR-198.95≥100 。

(10)

由式(9)得RMR≥-44.10，由式(10)得RMR≥27.37。因此，当27.37>RMR≥0时，式(3)不再适用；而当RMR取满整个区间，即当100≥RMR≥0时，式(2)都适用。因此，式(2)比式(3)更适合作为研究对象。

由于式(2)为“平均函数式”，所以对于坡高修正前的RMR和坡高修正后的(RMR)h都适用，将RMR和(RMR)h分别代入式(2)可得：

BQ=2.608 8RMR+215.06 ；

(11)

(BQ)h=2.608 8(RMR)h+215.06 。

(12)

式中(BQ)h为经过坡高修正后的BQ值，与(RMR)h相对应。将式(11)和式(12)相减再整理可得

(13)

等效指标比ke可用于RMR和BQ之间的关系换算，因此可令式(13)中的RMR/BQ=1/ke=1/6.927 3，同时将式(8)代入式(13)，再将式(13)按照式(8)的形式变形整理后，即可给出适用于BQ法边坡岩体质量分级的坡高修正系数ξb的计算公式，即

(14)

令ξb=1，解出坡高H=80.02 m，此时的H为参考坡高Hr，与CSMR分类体系中所设定的参考坡高Hr=80 m一致，由此可见式(14)给出的ξb是合理的。

4 应力状态影响修正系数

地应力是引起矿山、水利水电、土木建筑等地下或露天岩土开挖工程变形和破坏的根本作用力，是影响工程岩体稳定性的重要因素，因此，在工程岩体分级(尤其是稳定性分级)时，工程岩体的应力状态是影响岩体质量指标的修正项之一。在边坡岩体质量分级中，对于高度较低和坡度较缓的边坡可忽略应力状态的影响；而对于处于高地应力区的河流深切或人工开挖的高陡边坡，则不能忽略其影响，需根据岩体的应力状态进行适当修正。

4.1 应力状态指标

岩体内地应力的高低程度可通过应力状态指标来进行描述。最大主应力σ1是岩体地应力分析中的重要指标，岩石饱和单轴抗压强度Rc是常用的岩石强度参数，对于同一种岩石，Rc可认为是一个常量，因此，通常采用岩石饱和单轴抗压强度Rc和最大主应力σ1的比值Rc/σ1作为应力状态指标来描述地应力的高低程度。显然，Rc/σ1越小意味着地应力越高，反之则意味着地应力越低。

最大主应力σ1可通过现场地应力测量给出，但其测量所需的时间较长，成本较高，有时由于地质条件复杂，甚至无法获得理想的测量值，这些都不利于Rc/σ1在应力状态影响修正中的应用。因此，可以考虑采用其他与σ1相关且容易获取的岩体应力指标来估算σ1。岩体的自重应力σH和最大主应力σ1同属于地应力的范畴，且自重应力σH可直接通过岩体重度γr和上覆岩体厚度hr的乘积γrhr给出，因此可以考虑根据自重应力σH来估算最大主应力σ1，从而更方便地给出Rc/σ1的值。

在地应力测量过程中，不仅会给出最大主应力σ1的测量值，还会记录相应测量点的岩性和埋深等测量信息，通过岩性可推测出岩体重度γr，埋深近似为上覆岩体厚度hr，从而估算出该测量点的自重应力σH。通过查阅相关文献中的地应力测量结果，计算出同一测点最大主应力σ1和自重应力σH的比值σ1/σH，以测点埋深hr为x轴，以σ1/σH为y轴，对所有测点进行曲线拟合，设定拟合函数的边界条件：①在地面附近，即当hr→0时，σ1/σH→；②在深部岩体，即当hr→时，σ1/σH→1。根据边界条件给出拟合函数：σ1/σH=ahrb+1(a>0,b<0)，拟合结果如图2所示。

图2 σ1/σH和hr的关系拟合结果Fig.2 Fitting result between σ1/σH and hr

拟合结果表明σ1/σH和hr之间具有良好的非线性函数关系，具体函数关系式为

σ1/σH=1 559.633 25hr-1.346 23+1 。

(15)

式(15)满足设定的边界条件，且拟合相关系数较高，能较好地描述σ1/σH和hr之间的关系。当缺乏相关条件时，可通过式(15)估算最大主应力σ1，进而给出应力状态指标Rc/σ1，以此提高分级效率。

4.2 应力状态影响修正系数的取值标准

在确定应力状态影响修正系数之前，首先要判断边坡岩体是否处于高地应力状态，若处在非高地应力状态则无需修正，即修正系数取0。《国标》以Rc/σ1为应力状态评价指标来判别岩体是否处于高应力状态。具体判别标准如下：当Rc/σ1<4时，岩体处于极高地应力状态；当4≤Rc/σ1≤7时，岩体处于高地应力状态；当Rc/σ1>7时，岩体处于低地应力状态。本文采用的判别标准与此一致。

《国标》BQ法在地下工程岩体分级中给出了地应力状态影响修正系数及其取值标准[9]。地应力状态对地下工程岩体(尤其是深部岩体)的稳定性影响较大，因此在地下工程岩体分级中，地应力状态影响系数的取值下限和上限都较高。虽然边坡工程岩体的稳定性也受到地应力状态的影响，但其程度比不上地下工程岩体，因此，本文将地下工程岩体分级中的地应力状态影响修正系数的取值下限和上限均适当降低，给出了适用于边坡工程岩体分级的地应力影响修正系数K6的取值标准，具体如表3所示。

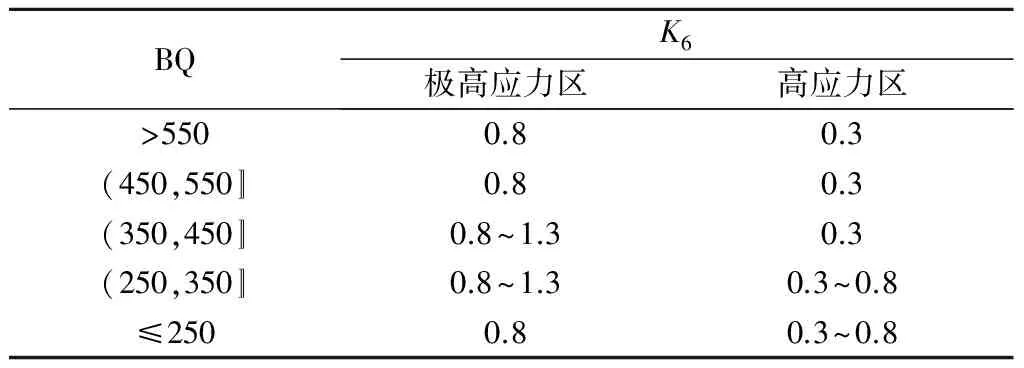
表3 应力状态影响修正系数K6的取值标准Table 3 Valuing criterion of correction factor K6 affected by stress condition

5 结构面性状影响修正系数

《国标》边坡[BQ]计算公式中的结构面类型与延伸性修正系数λ的评价指标较为笼统，仅对结构面做了简单的分类和描述，忽略了结构面的风化程度、起伏粗糙状况、填充物和张开度等因素对结构面性状的影响。这些因素的综合作用会导致结构面出现2种情况：①结构面的类型和延伸性相近，然而其实际表现出来的对岩体质量的影响程度却相差较大；②结构面的类型和延伸性不一致，然而其实际对岩体质量的影响程度却相近。由此可见，仅包含结构面的类型和延伸性，难以较全面地衡量结构面性状对岩体质量的影响程度。因此，本文建议将《国标》现有的“结构面类型与延伸性修正系数”修改为“结构面性状影响修正系数”，并将其评价指标由笼统的结构面类型和延伸性划分，细分为结构面的风化程度、起伏粗糙状况、填充物和张开度等主要性状，在保持《国标》中λ原有取值范围不变的条件下，将取值点根据性状的搭配组合进一步细化，优化后的具体取值标准如表4所示。

表4 结构面性状影响修正系数取值标准Table 4 Valuing criterion of correction factor impacted by structural plane character

6 优化后的边坡[BQ]计算公式

在《国标》中给出的边坡[BQ]计算公式的基础上，对修正系数及其取值标准做适当的补充和优化：①补充了坡高影响修正系数ξb及其计算方法；②补充了地应力影响修正系数K6及其计算方法、取值标准；③将《国标》现有的“结构面类型和延伸性修正系数λ”修改为“结构面性状影响修正系数λ”，并将其评价指标进行细化后给出了相应的取值标准。在上述研究成果的基础上，本文给出了优化后的边坡[BQ]计算式，具体为

[BQ]=ξbBQ-100(K4+λK5+K6)。

(16)

式中：K4和K5分别为《国际》中原有的边坡工程地下水影响修正系数和边坡工程主要结构面产状影响修正系数，取值方法与《国际》给出的一致。

式(16)中补充了坡高影响修正系数ξb和地应力影响修正系数K6，细化了结构面性状影响修正系数λ，因此，在应用于复杂地质条件下的高陡边坡岩体分级时更具优势，进一步明确了式(16)的适用范围。式(16)较为全面地考虑了各种影响边坡稳定性的重要因素，因此所计算出的边坡[BQ]不仅可以用于划分边坡岩体质量等级，还可以用于边坡稳定性评价。研究表明BQ岩体等级和RMR岩体等级之间存在着一定的对应关系[20]，而由RMR法衍生出的边坡岩体分级法(如SMR，CSMR，HSMR，TSMR，GSMR等)都有边坡稳定性评价系统。本文通过研究BQ岩体等级和RMR岩体等级的对应关系以及各种RMR衍生分级法的边坡稳定性评价系统，给出了BQ法边坡稳定性评价系统 (见表5)。该系统在稳定性评价的基础上，给出边坡岩体的可能破坏模式和加固措施建议，对工程实践具有较好的参考和应用价值。

表5 BQ法边坡稳定性评价系统Table 5 Slope stability evaluation system of BQ method

7 结 论

通过对《国标》边坡[BQ]计算公式中修正系数的计算方法和取值标准的研究和优化，得出以下主要结论和研究成果：

(1)现有《国标》中的边坡[BQ]计算公式的修正项和修正系数评价指标存在改进和完善的空间，在应用过程中不仅影响了分级结果的客观性和准确性，而且限制了BQ法在边坡工程岩体稳定性评价中的推广和发展。因此，有必要对边坡[BQ]计算公式进行优化和完善。

(2) 对RMR和BQ之间的线性函数关系进行了深入研究，提出了等效指标和等效指标比的概念。在此基础上，结合CSMR法中的坡高修正系数ξr计算公式，推导出了适用于BQ法的坡高修正系数ξb计算公式，并且通过参考坡高Hr对ξb计算公式进行了合理性检验。检验结果表明，ξb和ξr对应的参考坡高Hr皆为80 m，证明ξb计算公式是合理的。

(3)以现场地应力测量数据为基础，在设定的边界条件下，通过曲线拟合的方式给出了岩体最大主应力σ1和自重应力σH的比值σ1/σH与岩体埋深hr之间的函数关系。当缺乏地应力测量条件和测量数据时，可通过σ1/σH和hr的函数关系估算最大主应力σ1，从而更加便捷地给出应力状态评价指标Rc/σ1的值。参照《国标》地下[BQ]计算公式中的应力状态影响修正系数取值标准，同时考虑边坡工程通常的实际应力状态，给出了用于边坡[BQ]计算的应力状态影响修正系数K6的取值标准。

(4)将《国标》中原有的“结构面类型和延伸性影响修正系数λ”修改为“结构面性状影响修正系数λ”，后者较前者在评价指标的分类和描述上更为细化和具体，充分考虑了张开度、填充物、起伏粗糙状况和风化程度等因素对结构面性状的影响，对前者的评价指标在分类和描述上进行了改进和完善。在保持《国标》中λ原有取值范围不变的条件下，将取值点根据性状的搭配组合进一步细化，给出了优化后的λ取值标准。

(5)在《国标》边坡[BQ]计算公式的基础上，对修正系数及其取值标准做适当的补充和优化，使其更适用于复杂地质条件下的高陡边坡岩体分级，并给出了优化后的边坡[BQ]计算公式。通过研究由RMR法衍生出的多种边坡岩体分级法中的边坡稳定性评价系统，并结合RMR等级和BQ等级之间的对应关系，给出了适用于BQ法的边坡稳定性评价系统。

[1] HACK R. Slope Stability Probability Classification (SSPC)[M].Delft：International Institute for Aerospace Survey and Earth Sciences，1996：258.

[2]HACK R. An Evaluation of Slope Stability Classification[C]∥ International Society for Rock Mechanics and Rock Engineering, ISRM International Symposium-EUROCK 2002, Madeira, Portugal, November 25-27, 2002：3-32.

[3] HACK R，PRICE D，RENGERS N. A New Approach to Rock Slope Stability—A Probability Classification (SSPC)[J]. Bulletin of Engineering Geology and the Environment，2003，62(2)：167-184.

[4] SHUK T. Key Elements and Applications of the Natural Slope Methodology (NSM) with Some Emphasis on Slope Stability Aspects[C]∥Proceedings of the 4th South American Conference on Rock Mechanics. Santiago de Chile：Pergamon Press，1994：255-266.

[5] GB 50330—2002，建筑边坡工程技术规范[S].北京：中国建筑工业出版社，2002：66-67.

[6] SL 386—2007，水利水电工程边坡设计规范[S].北京：中国水利水电出版社，2009：43-44.

[7] BIENIAWSKI Z T.Rockmass Classifications in Rock Engineering[C]∥ International Society for Rock Mechanics and Rock Engineering， Symposium on Exploration for Rock Engineering, Johannesburg, November 1-5, 1976. Rotterdam：Balkema，1976：97-106.

[8] BIENIAWSKI Z T. Engineering Rockmass Classifications[M].New York：Wiley，1989：251.

[9] GB/T 50218—2014，工程岩体分级标准[S].北京：中国计划出版社，2015.

[10] ROMANA M. New Adjustment Ratings for Application of Bieniawski Classification to Slopes[C]∥Proceedings of the International Society for Rock Mechanics and Rock Engineering. Zacatecas，Mexico： International Symposium on Role of Rock Mechanics，1985：49-53.

[11] ROMANA M. SMR Classification[C]∥International Society for Rock Mechanics and Rock Engineering，7th ISRM Congress, Aachen, Germany, September 16-20, 1991：955-960.

[12] 孙东亚，陈祖煜，杜伯辉，等.边坡稳定评价方法 RMR-SMR 体系及其修正[J].岩石力学与工程学报，1997，16(4)：297-304.

[13] 石豫川，王 哲，万国荣，等.山区高等级公路边坡岩体分级研究[J].岩石力学与工程学报，2005，24(6)：939-944.

[14] 张元才，黄润秋，赵立冬，等.天山公路边坡岩体质量评价TSMR体系研究[J].岩石力学与工程学报，2010，29(3)：617-623.

[15] 巫德斌，徐卫亚.岩石边坡力学参数取值的GSMR法[J].岩土力学，2005，26(9)：1421-1426.

[16] 张菊连，沈明荣.水电边坡岩体稳定性分级系统研究[J].岩石力学与工程学报，2011，30(增2)：3481-3490.

[17] 蔡 斌.国标《工程岩体分级标准》应用中的几个问题[J].岩土力学，2003，24(增刊)：74-76.

[18] 申艳军，徐光黎.国标岩体分级标准BQ的图解法表示[J].岩石力学与工程学报，2012，31(增2)：3659-3665.

[19] 李长雄.对现行工程岩体及隧道围岩分级标准的探讨[J].路基工程，2009，(4)：96-97.

[20] 蔡 斌，喻 勇，吴晓铭.《工程岩体分级标准》与Q分类法、RMR分类法的关系及变形参数估算[J].岩石力学与工程学报，2001，20(增刊)：1677-1679.

[21] 邬爱清，柳赋铮.国标《工程岩体分级标准》的应用与进展[J].岩石力学与工程学报，2012，31(8)：1513-1523.

[22] 魏云杰.中国西南水电工程区峨眉山玄武岩岩体结构特性及其工程应用研究[D].成都：成都理工大学，2007.

[23] 张 强.金沙江观音岩电站红层钙质砂岩类岩溶发育特征及渗透稳定性研究[D].成都：成都理工大学，2010.

[24] 李攀峰.大型地下洞室群围岩稳定性工程地质研究[D].成都：成都理工大学，2004.

[25] 张曙光.金沙江白鹤滩水电站高拱坝建设工程地质适宜性研究[D]. 成都：成都理工大学，2007.

[26] 王广德.复杂条件下围岩分类研究——以锦屏二级水电站深埋隧洞围岩分类为例[D].成都：成都理工大学，2006.

[27] 张占荣.裂隙岩体变形特性研究[D].武汉：中国科学院武汉岩土力学研究所，2010.

[28] 唐胜传.复杂场地高坝建设适宜性的工程地质研究[D].成都：成都理工大学，2002.

[29] 陈近中.双江口电站工程岩体质量分级研究[D].成都：成都理工大学，2007.

[30] 孙 苗.岩体质量分级的程序设计及应用[D].西安：长安大学，2011.

[31] 卢书强.澜沧江糯扎渡水电站地下洞室群岩体质量分级及其对围岩稳定性的控制作用[D].成都：成都理工大学，2004.

[32] 何江达，谢红强，王启智，等.官地水电站坝址区初始地应力场反演分析[J].岩土工程学报，2009，31(2)：166-171.

[33] 胡 斌，冯夏庭，黄小华，等.龙滩水电站左岸高边坡区初始地应力场反演回归分析[J].岩石力学与工程学报，2005，24(22)：4055-4064.

[34] 陈秀铜，李 璐.某水电站地下洞室群初始地应力场反演回归分析[J].岩土力学，2007，28(增)：540-544.

[35] 杨 强，刘福深，任继承.三维初始地应力场的多尺度弹塑性校正[J].水力发电学报，2007，26(6)：24-29.

[36] 蔡美峰，乔 兰，李长洪，等.深凹露天矿高陡边坡稳定性分析与设计优化[J].北京科技大学学报，2004，26(5)：465-470.

[37] 付成华，汪卫明，陈胜宏.溪洛渡水电站坝区初始地应力场反演分析研究[J].岩石力学与工程学报，2006，25(11)：2305-2312.

[38] 侯明勋，葛修润.岩体初始地应力场分析方法研究[J].岩土力学，2007，28(8)：1626-1630.

[39] 许传华，刁 虎，任青文，等.紫金山金铜矿初始地应力场反演分析[J].岩土力学，2009，30(2)：425-428，432.

[40] 金长宇，冯夏庭，张春生.白鹤滩水电站初始地应力场研究分析[J]. 岩土力学，2010，31(3)：845-850,855.

[41] 张建国，张强勇，杨文东，等.大岗山水电站坝区初始地应力场反演分析[J].岩土力学，2009，30(10)：3071-3078.

[42] 周 华，陈胜宏.高拱坝坝址区初始地应力场的二次计算[J].岩石力学与工程学报，2009，28(4)：767-774.