基于贯入阻力与含水率联测的黄土填方压实度检测方法
,,,,3,
(1.西安建筑科技大学 土木工程学院,西安 710055;2.机械工业勘察设计研究院有限公司 a.技术研发中心;b.陕西省特殊土工程性质与处理技术重点实验室,西安 710043;3.西安交通大学 人居环境与建筑工程学院,西安 710049)
1 研究背景
在填方工程中,压实度是施工管理最为关键的指标之一,直接关系到填方地基的强度、变形和稳定性。目前施工中常用的压实度检测方法有环刀法、灌砂法、灌水法等。这些传统检测方法虽然测试结果准确可靠,但属于有损检验,且存在抽样点少、检测速度慢、费用高等缺点,难以满足快速机械化施工要求。由于传统测试方法的不足,人们一直在寻找快速无损的压实度测试方法。国内外学者研究了EDG[1-2],SDG[3],MDI[4],TDR[5]等压实度快速检测方法,但上述方法一般在含水率、干密度较小的区间内使用,当含水率、干密度变化范围较大时,尚不能获得满意的测试效果。
普氏贯入仪是一种静力贯入式压实度检测设备,因设备简单、操作方便、效率高等优点,在大面积填方工程压实度和均匀性跟踪检测方面具有优势,并已在水利工程中得到应用[6-7]。普氏贯入仪的测试原理是将锥形探头采用静力压入被测土层内,同时依靠机械或电子器件测定土层的贯入阻力,利用在同一土类对比试验中建立的贯入阻力与压实系数(或干密度)之间的统计关系式来确定土层的密实程度[8]。同其他贯入式压实度检测方法类似,普氏贯入仪忽略了含水率变化对测试结果的影响。但对于类似黄土这样具有“水敏性”的特殊土,一方面含水率对其力学性质的影响较大;另一方面在大面积的削山造地工程中,由于就地挖山取材,黄土填料的含水率变化范围较大,单纯依靠测定贯入阻力大小,无法准确判定被测填土的压实情况,导致普氏贯入仪的测量精度偏低,难以在工程中广泛应用。因此,要使普氏贯入仪真正做到快速准确地测定填土压实度,必须考虑含水率对测试结果的影响,将静力贯入法与含水率的快速测试方法结合起来,建立考虑含水率变化影响的标定模型,以提高测试精度。
在众多土体含水率的快速测试方法中,利用土壤的介电特性来测量土壤的水分含量是一种有效的、快速的、简便的、可靠的方法[9-12]。目前,市场上的土壤水分传感器测量值是体积含水率,输出信号以电压信号为主,而工程上常采用质量含水率,但国内对土壤水分传感器输出电压与质量含水率之间的数学模型研究鲜见报道。
本文针对静力贯入式压实度检测方法中存在的问题,以黄土为研究对象,采用普氏贯入仪和土壤水分传感器同时测定黄土试样在不同含水率和干密度时的贯入阻力和土壤水分传感器输出电压,建立考虑含水率影响的数学模型,并检验了该数学模型对测定黄土填方含水率和干密度的精度和可行性。
2 试验概况
2.1 试验设备
本次采用的试验设备主要包括普氏贯入仪和便携式土壤水分速测仪。普氏贯入仪主要组件包括锥形探头、贯入杆、测力传感器、施力手柄等。其中测力传感器量程为1 000 N,精度为±0.5%FS(FS为满量程),标准测试深度为0~30 cm,贯入杆加长后测试深度可达到1.5 m。试验采用的锥形探头直径为8 mm,与探头相连的贯入杆直径为7 mm。
便携式土壤水分速测仪由探针式土壤水分传感器和读数仪组成,可方便、快速地测量体积含水率,测试结果以模拟电压形式输出,由读数仪计算并显示。土壤水分传感器的探头上带有4根同心探针,探针长度为7 cm,90%的测量区域分布在以中央探针为中心,直径为3 cm、高为7 cm的圆柱形区域内。土壤水分传感器体积含水率测量范围为0%~50%,精度为±2%(标定后),响应时间<1 s,输出电压范围为0~2 500 mV。
2.2 试验用土的基本性质
试验用土取自陕北某大面积黄土填方工程,原始地形起伏较大,属典型的黄土丘陵沟壑区,地层分布稳定,土质均匀,结构较致密。试验用土为马兰黄土,颗粒组成以粉土为主,硬塑。天然黄土的基本物理性质指标如表1所示。

表1 天然黄土的基本物理性质指标Table 1 Basic physical properties of natural loess samples

图1 颗粒分析曲线Fig.1 Curve of particle-size distribution
根据《土工试验方法标准》[13]得到试验土样的颗粒分析曲线,如图1所示。本次试验黄土的不均匀系数Cu=5.63,曲率系数Cc=1.34,平均粒径D50=0.04 mm。采用重型击实试验测定的黄土最优含水率为12.1%,最大干密度为1.86 g/cm3。
在黄土丘陵沟壑区开展的大面积造地工程中,黄土填料是从黄土梁峁处开挖后直接填筑,天然含水率变化较大。试验前,随填筑施工随机采集了449组料源土样进行含水率统计分析,分析结果如图2所示。料源黄土的含水率分布区间较广,其中8%~20%含水率区间内的样本数量约占样本总数的90%。因此,本次试验参照含水率统计分析结果及重型击实试验结果,试验土样的含水率为7.8%,9.3%,12.1%,13.9%,15.9%,18.2%,19.9%,压实系数变化范围为0.81~1.00,以模拟实际工程的主要含水率区间。
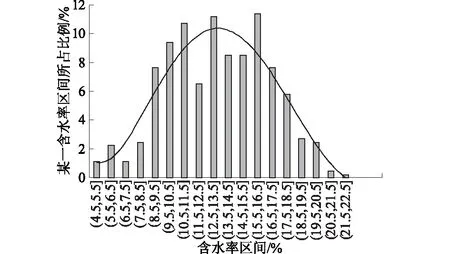
图2 黄土填料的含水率统计结果Fig.2 Statistical result of water content of loess filling
2.3 试验方法与过程
制样时,土料经过筛(2 mm)、拌和、闷料和称重后,根据设计干密度及含水率制备直径为30 cm、高为25 cm的试验土样。
测试时,首先将土壤水分传感器探针插入试样中,读取土壤水分传感器输出电压。然后将普氏贯入仪的贯入杆垂直对准并紧贴土体表面,对贯入手柄施加向下的静压力,使贯入杆在10~15 s的时间内平稳、匀速地贯入到土体内部。当贯入深度达到10 cm后,停止贯入,记录贯入阻力峰值。对同一土样分别测试3组贯入阻力数据,剔除异常数据后,取平均值作为测试结果。最后采用灌砂法和烘干法测定试样干密度和质量含水率,并由式(1)换算为烘干法体积含水率θw。
θw=wρd/ρw。
(1)
式中:ρd为灌砂法实测干密度(g/cm3);ρw为纯水密度(g/cm3),取1.0 g/cm3;w为质量含水率(%)。
3 试验结果分析与模型建立
室内试验结果汇总如表2所示。灌砂法、烘干法测试结果较准确,可分别作为干密度、含水率测试的标准方法,普氏贯入仪、土壤水分传感器基于灌砂法、烘干法实测结果进行分析与建模。
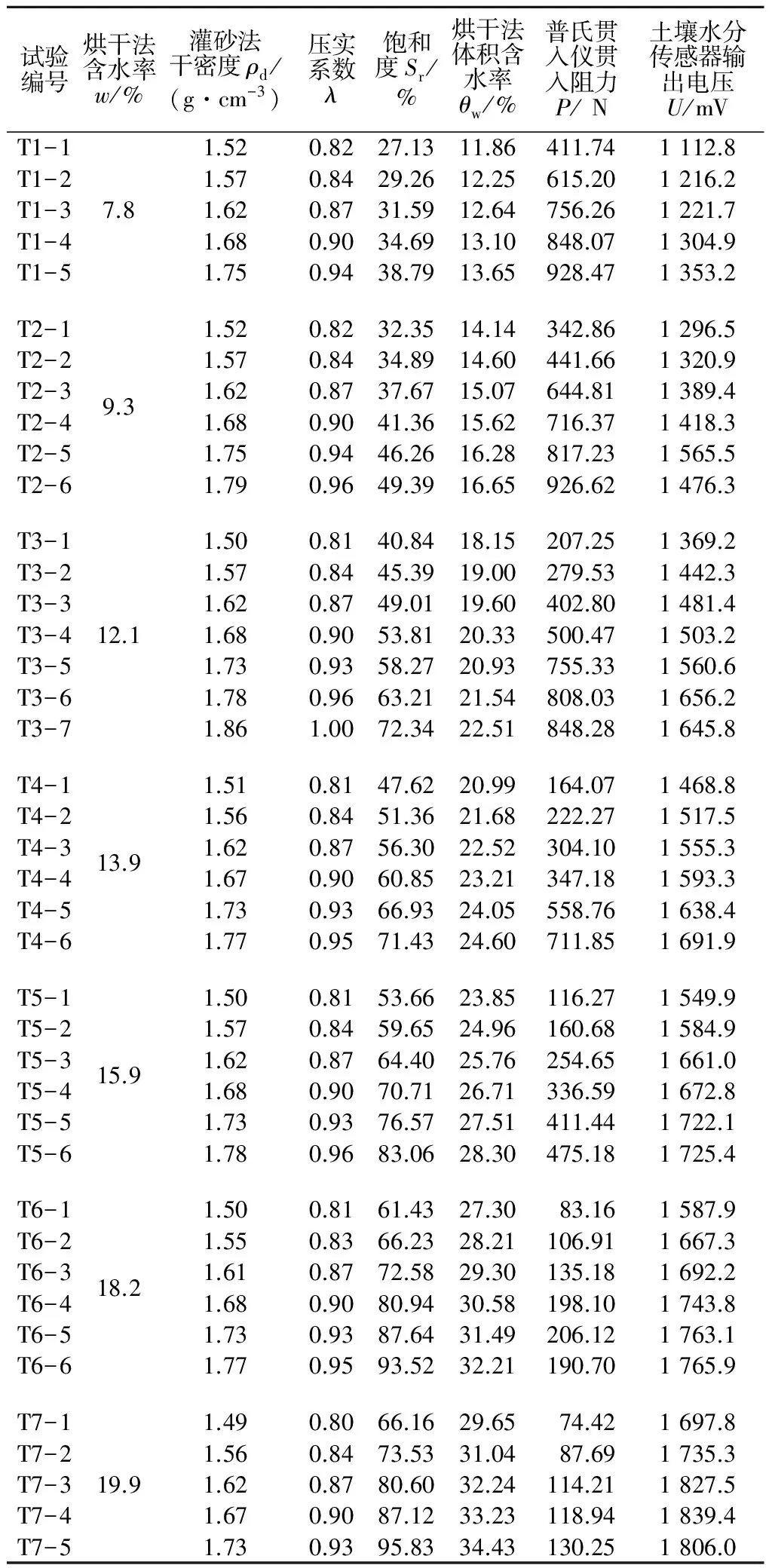
表2 试验结果汇总Table 2 Summary of test results
3.1 贯入阻力与含水率、干密度的相关性分析
贯入阻力与干密度关系曲线如图3所示。由图3可知,当含水率单因素变化时,贯入阻力与干密度之间近似呈线性关系,即
(2)

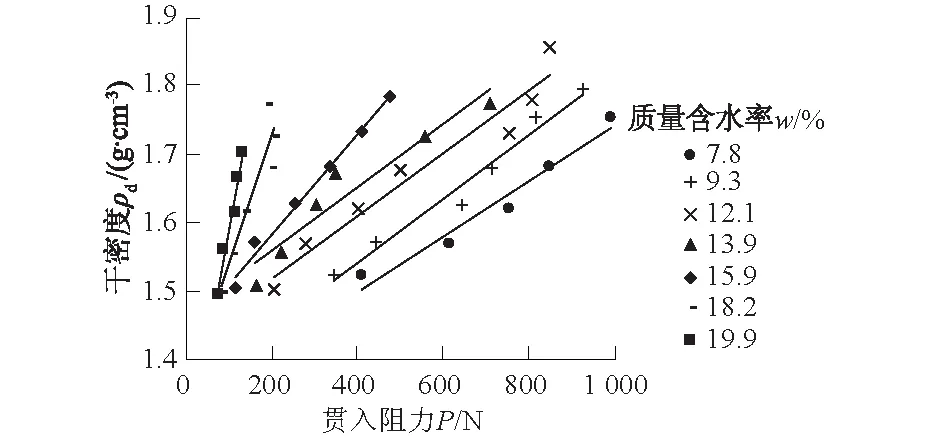
图3 贯入阻力与干密度关系Fig.3 Relation between penetration resistance and dry density
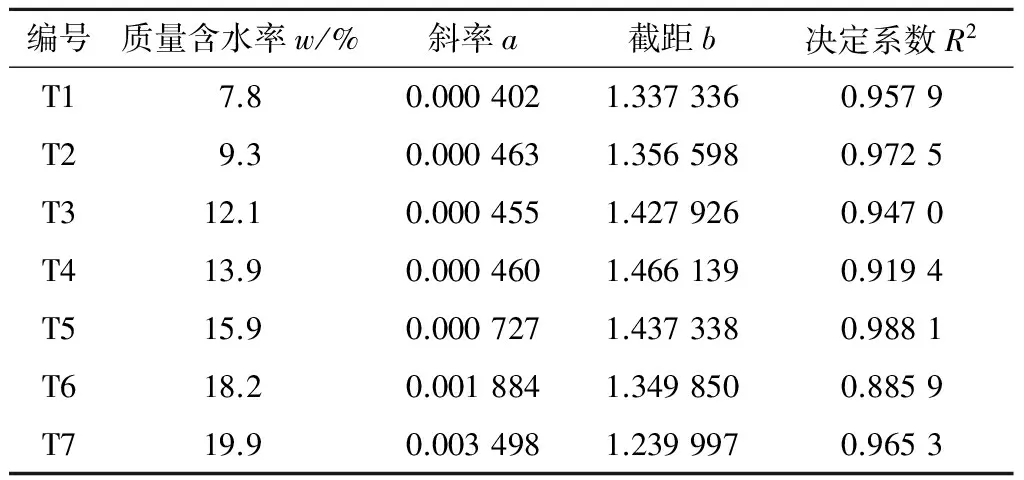
编号质量含水率w/%斜率a截距b决定系数R2T17.80.0004021.3373360.9579T29.30.0004631.3565980.9725T312.10.0004551.4279260.9470T413.90.0004601.4661390.9194T515.90.0007271.4373380.9881T618.20.0018841.3498500.8859T719.90.0034981.2399970.9653
图3中,在低含水率区间7.8%≤w≤13.9%内,a值较接近,即贯入阻力随干密度变化的幅度较接近;在高含水率区间13.9% 图4为贯入阻力与含水率关系曲线。贯入阻力的变化可以很好地反映土体软硬程度的变化过程,表征土体的力学性能。相同压实系数、不同含水率下,压实黄土的贯入阻力随含水率的增大而快速下降。以压实系数λ=0.90的试验结果为例,含水率从7.8%变化至19.9%,其贯入阻力从848.07 N变化至118.94 N,相差了超过7倍。因此,单纯依靠测定贯入阻力大小,无法准确判定压实情况。 图4 贯入阻力与含水率关系曲线Fig.4 Curves of penetration resistance vs. water content 由试验土样干密度与贯入阻力间的线性回归得到传统线性回归模型Ⅰ,如图5所示。当采用表2中含水率变化范围为9.3%≤w≤13.9%的试样(在wop±3%以内,wop为最优含水率)进行线性回归,决定系数R2=0.803 1;当采用表2中含水率变化范围为7.8%≤w≤19.9%的试验土样进行线性回归,决定系数R2=0.382 3,标定模型的相关性均较低,拟合效果较差。由图2可知,施工现场黄土填料的含水率变化范围较大,很难控制在最优含水率附近,因此不宜通过最优含水率附近的线性回归方程来评价较大含水率变化范围内的填方压实度。 图5 贯入阻力与干密度线性回归方程Fig.5 Linear regression equations between penetration resistance and dry density 为提高普氏贯入仪的测试精度,需要对传统标定模型进行修正,建立考虑含水率变化对贯入阻力影响的修正模型,以提高测试精度。将表3中a,b值与质量含水率w之间的关系采用最小二乘法进行回归分析(见图6),可得到回归方程式(3)、式(4)。 (3) b=-0.000 354w3+0.010 055w2- 0.069 871w+1.431 855 。 (4) 图6 参数a,b与质量含水率w的关系Fig.6 Relations between parameters a, b and mass water content w 将式(3)、式(4)中的参数a,b代入式(2),可得到考虑含水率变化对贯入阻力影响的标定模型,该标定模型为包含贯入阻力P和质量含水率w的二元分段函数。该模型提高了标定模型的计算精度,但是若质量含水率w仍采用烘干法测定,无疑会降低检测速度,因此,该方法需要与含水率的快速测试技术相结合,以提高检测效率。 结合现场实际工况,试验温度与现场填土检测层的平均地温近似 (取(14±2)℃)。图7为含水率单因素变化时,土壤水分传感器输出电压与干密度的关系曲线。 图7 土壤水分传感器输出电压与干密度的关系Fig.7 Relation of the output voltage of soil moisture sensor against dry density 由图7可知,当含水率变化范围为7.8%≤w≤19.9%时,土壤水分传感器输出电压与干密度近似呈线性关系,二者关系可表示为 ρd=cU+d。 (5) 式中:U为土壤水分传感器输出电压(mV);c,d为拟合参数,由表2中同一含水率下的试验数据线性回归得到,线性回归结果详见表4。 表4 不同含水率下土壤水分传感器测试数据 线性回归参数Table 4 Parameters of linear regression for soil moisture sensor corresponding to different water content 将式(5)代入式(1)中,并将烘干法体积含水率θw采用土壤水分传感器的体积含水率测试值θv(由θv与U之间的标定方程确定)替换,得到 w=θvρw/(cU+d) 。 (6) 图8为表4中T1—T5组的参数c,d与质量含水率w的线性回归结果,回归方程分别为 c=ew+f; (7) d=gw+h。 (8) 图8 拟合参数c,d与质量含水率w的线性回归方程Fig.8 Linear regression equations between parameters c,d and mass water content w 回归参数e,f,g,h数值分别为:e=0.000 054,f=0.000 499,g=-0.130 431,h=1.492 325。将式(7)、式(8)代入式(6)可得式(9)。 w=ρwθv/[(ew+f)U+gw+h] 。 (9) 求解式(9)中关于质量含水率w的一元二次方程,得到质量含水率w关于U,θv的数学关系式为 (10) 土壤水分传感器可由式(10)直接得到质量含水率测试值,将该值代入式(3)、式(4),求得参数a,b值,然后将a,b值代入式(2)即可得到考虑含水率对贯入阻力影响的标定模型Ⅱ。 表5 验证标定模型的试验数据Table 5 Test data for the verification of calibration models 为验证模型的可靠性,在填方工地现场随机选择8处试验点,采用前述标定模型分别计算试样的含水率或干密度,并基于烘干法、灌砂法测量值分析各标定模型的计算误差。将烘干法质量含水率实测值、灌砂法干密度实测值作为“真实值”,计算绝对误差和相对误差。检验标定模型的试验数据见表5。 由表5中的统计结果可知,当质量含水率变化范围为8.3%≤w≤19.2%,采用土壤水分传感器得到的质量含水率测试值与烘干法测量值绝对误差范围为-1.55%~2.15%;采用传统线性回归模型Ⅰ(不考虑含水率变化因素影响),干密度测试值与灌砂法测量值的绝对误差范围为-0.15~0.09 g/cm3,相对误差范围为-8.75%~5.91%;采用考虑含水率对贯入阻力影响的标定模型Ⅱ,干密度测试值的绝对误差范围为-0.10~0.04 g/cm3,相对误差范围为-5.97%~2.44%。与传统线性回归模型Ⅰ相比,采用考虑含水率对贯入阻力影响的标定模型Ⅱ,其测量精度有大幅度提高,表明该模型具有较好的可靠性。 本文提出的基于贯入阻力和含水率联合测试、数据融合建模的压实度快速检测方法,可有效降低单独采用普氏贯入仪时,因含水率变化引起的误判问题,提高了压实度的检测精度。未来有望将普氏贯入仪与土壤水分传感器集成,形成一体化设备,使用更为方便。 本文提出的检测方法可尝试用于大面积填方工程,施工、监理单位对填土压实度和均匀性的现场快速评定,与传统方法配合进行填土压实度检测,提高总体检测效率。考虑到该方法在检测过程中需要测定土体的贯入阻力和土壤水分传感器输出电压,需将仪器的探头(针)插入被测土层,因此土的粒径不宜过大。除已验证适用黄土外,在其他黏性土、粉土、细砂等细颗粒土的填方工程中也具有应用前景,但不适合用于碎石土、风化岩、粗砂和砾石等较粗的填料,相关应用效果需要后续研究进行验证。 (1)当质量含水率单因素变化时,贯入阻力与干密度之间近似呈线性关系。检验结果表明,当质量含水率变化范围为8.3%≤w≤19.2%,采用干密度ρd与贯入阻力P间的传统线性回归模型Ⅰ,干密度测试值与灌砂法测量值的绝对误差范围为-0.15~0.09 g/cm3,相对误差范围为-8.75%~5.91%。 (2)同一含水率下,土壤水分传感器输出电压与干密度近似呈线性关系。检验结果表明,当质量含水率变化范围为8.3%≤w≤19.2%,采用土壤水分传感器得到的质量含水率测试值与烘干法测量值的绝对误差范围为-1.55%~2.15%。 (3) 当质量含水率变化范围为8.3%≤w≤19.2%时,采用考虑含水率对贯入阻力影响的标定模型Ⅱ,干密度测试值与灌砂法测量值的绝对误差范围为-0.10~0.04 g/cm3,相对误差范围为-5.97%~2.44%,相较传统线性回归模型Ⅰ,测试精度明显提高。 (4)本文提出的基于贯入阻力与含水率联测的压实度检测方法,明显提高了现有贯入式压实度检测方法的精度,未来有望开发集贯入阻力、含水率测试功能为一体的压实度检测设备。该方法经试验检验适用于黄土,在其他各类土质中的适用性尚需进一步验证。 [1] CHRISTOPHER L M, JASON S H. Using Electrical Density Gauges for Field Compaction Control[R].Newark:University of Delaware,2011. [2] 郑建国,羊群芳,刘争宏,等.EDG无核密度仪标定模型与测试误差的试验研究[J].岩石力学与工程学报,2016,35(8):1697-1704. [3] 顾欢达,薛国强,胡 舜,等.SDG密度仪路基压实度检测及效果评价[J].北京工业大学学报,2013,39(12):1835-1842. [4] 季建兵,宋蓓蓓.MDI无核密度仪在试验检测中的应用初探[J]. 人民长江,2009,40(12):25-26. [5] 陈 赟,陈 伟,陈仁朋,等.TDR联合监测土体含水量和干密度的传感器的设计及应用[J].岩石力学与工程学报,2011,30(2):418-426. [6] 朱海江.普氏贯入仪在水利工程筑坝中的应用[J]. 地基处理,2002,13(3):50-52. [7] 聂志坚,丁再涛,李 可.电子智能普氏贯入仪与环刀法对比检测在砂坝上的应用[J].中国水利,2002,(11):68. [8] 范 云.填土压实质量检测技术的发展与评析[J].岩土力学,2002,23(4):524-529. [9] 赵燕东,张一鸣.基于驻波率原理的土壤含水率测量方法[J]. 农业机械学报,2002,33(4):109-111,121. [10] 赵燕东,王一鸣.基于驻波率原理的土壤水分传感器的测量敏感度分析[J].农业工程学报,2002,18(2):5-8. [11] 张志勇.基于驻波率原理的土壤水分测量方法的研究[D]. 太原:山西农业大学,2005. [12] 张 益,马友华,江朝晖,等.土壤水分快速测量传感器研究及应用进展[J].中国农学通报,2014,30(5):170-174. [13] GB/T 50123—1999,土工试验方法标准[S].北京:中国计划出版社,1999.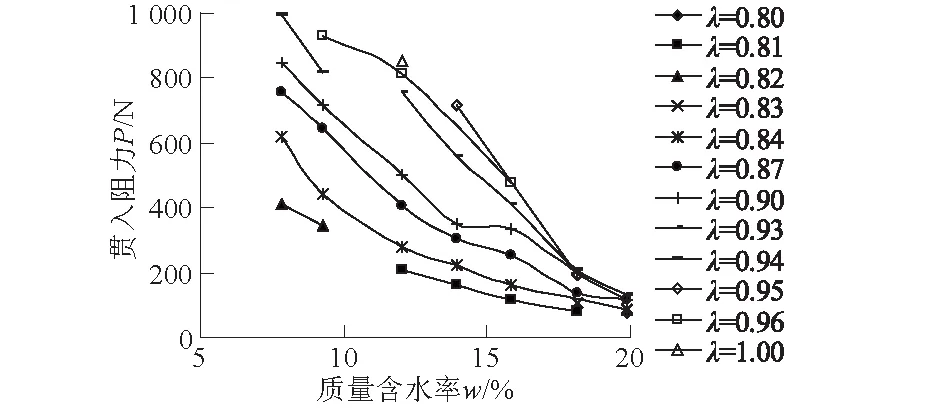



3.2 质量含水率与土壤水分传感器输出电压的关系
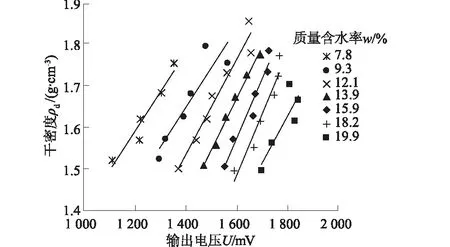



3.3 模型的可靠性检验
4 关于检测方法适用性的讨论
5 结 论

