基于孔内超声扫描技术的空区立体轮廓确定方法

，，

(1.中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室，武汉 430071；2.中国科学院大学,北京 100049)

1 研究背景

随着我国社会、经济的迅猛发展，矿产资源的需求急剧增加，而矿产资源地下开采不可避免会形成大量的采空区[1]。采空区的存在会导致矿山开采条件恶化，有可能引发井下大面积冒落、岩移及地表塌陷，造成严重的人员伤亡和设备破坏[2]。岩溶的发育对油气资源的富集与运移、地下水资源的分布与径流、与岩溶相关矿产资源的发育和分布以及工程建设都能产生重要影响。此外，岩溶造成的地质灾害日渐频繁，带来的损失不可估量[3-4]。地下能源储存一般放置在盐岩、非渗透性岩层以及多孔隙岩层中，国际上公认盐岩体是能源(石油、天然气)储存最理想的介质，世界上90%的能源(石油、天然气)储存库建在盐岩介质或报废的废盐矿井中[5]。因此，对于地下深部的空区探测尤为重要。

地下空区的形成原因较为复杂，空区的水平断面在不同深度往往不相同，为保证工程质量以及服务各项科学研究，需要及时、准确地测量和分析地下空区在不同深度处的截面形状，这对于确定空区走向、防止空区塌陷以及保证工程质量都有重要意义。目前所采用的孔内超声扫描探测技术，主要是通过电机旋转带动超声换能器，从而实现空区水平断面的360°扫描，水平断面扫描的数据点越多，则轮廓曲线越光滑，与实际形状更接近。但由于采集速度和存储空间的限制，通常只能探测水平断面的部分离散点，通过拟合来实现水平断面的轮廓绘制，在钻孔方法(纵向)上采用直接连接水平断面的方式来形成地下空区的立体图形。

由于深部地下空区探测环境极其复杂，往往在水平断面上只能得到有限的探测数据点，在同一水平断面测量的坐标点较少的情况下，希望拟合的截面封闭曲线能够通过所有测得的坐标点，同时能够比较光滑地拟合出水平断面空区岩壁的形状，而采用线性插值得到的水平断面的形状很粗糙，只有经验丰富的工程师才能给出可靠准确的数据解释和探测结论。此外，由于空区的岩壁是极其不规则的，光滑性好的抛物线插值、三次样条插值也不适合空区岩壁的轮廓拟合，最小二乘法[6-9]只能拟合出有效圆。针对现有技术的不足，本文提出了一种空区立体轮廓确定方法，以解决地下空区立体轮廓的绘制问题。

2 孔内超声扫描探测技术

孔内超声扫描探测系统主要通过超声换能器发射和接收声波信号，声波信号遇到空区岩壁后发生反射，根据信号发射和接收所用时间来计算出换能器与岩壁之间的水平距离；采用步进电机带动换能器水平旋转，实现空区岩壁的水平断面扫描，根据换能器所处的方位以及测量点距离拟合出能够正确反映空区岩壁的水平断面实际轮廓曲线；再根据换能器所处深度拼接成地下空区的立体轮廓。

图1 系统结构原理Fig.1 Schematic diagram of system structure

孔内超声扫描探测系统结构原理如图1所示，系统在孔内的部分主要包括超声换能器、旋转电机、电子罗盘、探头电路和传输电缆等，地面部分主要包括具有计量深度的深度绞车、电源/信号控制箱、通讯线以及计算机等。

包含换能器、旋转电机和电子罗盘等部件的孔内探头通过电缆垂直悬吊于钻孔中，电缆与有计量深度的绞车相连接，深度绞车连接地面上的控制箱，控制箱与计算机相连接，实现空区轮廓的实时显示和存储；通过深度绞车垂直下放孔内探头，由孔内探头测得地下空区各深度水平断面的轮廓数据，由深度绞车测量下放电缆的长度，从而获取钻孔内空区的深度数据，空区各断面轮廓数据和对应深度数据同时传输到计算机中，实现空区轮廓的立体扫描。

3 数据预处理

在孔内超声扫描探测系统的勘测过程中，探测系统电路本身的随机扰动会产生噪声信号；此外，孔内探头周围的环境会对数据采集产生干扰影响，如泥浆中存在的气泡和岩石碎屑；探头在下放过程中，也会因不停颤动而形成噪声信号。噪声信号的存在不仅给空区断面轮廓的确定带来困难，同时也给空区特征区域走向造成很大误差。

(1)

式中rh,i为超声换能器在深度h处第i个有效采样点的值，即换能器中心与空区岩壁的距离。判决条件为

(2)

式中：Nmin和Nmax分别为设置的阈值;Nmin为≤1的正数，Nmax为≥1的正数。根据孔内空区的实际情况选择合适的值，阈值不易设置太大或者太小，否则当某一区域噪声较多时滤波效果不理想。

从起始点开始，判断当前点与前一点的差值，若两点之间无突变,仍然保留该点原始值，否则对其平滑处理(有效值记为前后2个有效值点的平均值)。由于测量数据点较多，即便在同一测量位置，也不能保证返回的超声信号完全相同，因此，找到一个相对准确的起始点较为重要。各水平断面采集到的前3个数据点的有效值视为四分之一圆周内距离的平均值，记为

(3)

4 立体轮廓确定方法

根据超声测距原理，在钻孔内不同深度的水平断面上对空区岩壁进行每周n个点的测距扫描，将n个数据点通过曲线拟合，可以描绘出水平断面的轮廓曲线，然后将各水平断面轮廓根据深度顺序叠加，形成空区的立体轮廓。在实际勘测中，由于地质条件和空区形状的不同，超声波回波的强弱相差很大，甚至在很多点上得不到回波，此外，为了提高勘测速度，只能获得有限的扫描数据点，因此，本文在有效扫描数据点不多的情况下，采用Bezier曲线进行水平断面轮廓拟合来减少轮廓拟合误差。

4.1 坐标系的建立

在描绘轮廓曲线之前，需要建立空间直角坐标系，选取地表上垂直钻孔的中心点为坐标原点O，按照右手螺旋法则，选取原点指向地理正北方作为x轴，地理正东方作为y轴，钻孔走向为z轴，如图2所示。

图2 坐标系示意图Fig.2 Schematic diagram of coordinate system

根据空间直角坐标系的表述，地下空区岩壁上的任意一点P可表示为(xp,yp,zp)，将P点的直角坐标转化为柱坐标，其对应关系为

(4)

式中：hp为岩壁上扫描点所处的深度；rp为换能器与岩壁之间的探测距离；θp为换能器扫描线与地理北方的夹角。在钻孔的深度h处，换能器匀速旋转，能够获取整周的n个距离值rh,i，n个扫描点之间的旋转角度相等，假设Ph,i点为h深度上第i个扫描点，可以将Ph,i点的坐标描述为

(5)

4.2 水平断面曲线的确定

Bezier函数[10]是控制多边形的控制点关于Bernstein基函数的加权和。每个控制点Ci对曲线都有影响，改变Ci点的位置即可改变曲线的形状，n次Bezier曲线如图3所示。

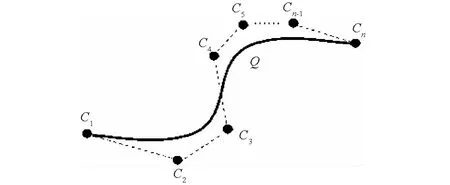
图3 n次Bezier曲线Fig.3 N times Bezier curve

Bezier曲线的阶次随着控制多边形顶点数目的增加而增加，高次Bezier曲线由>3个的顶点来确定曲线，计算起来代价很高，而且容易有数值舍入误差，而二次Bezier曲线通过3个顶点就可以确定曲线，计算过程较为简单。因此，本文采用二次Bezier曲线进行空区岩壁的水平断面轮廓拟合，二次Bezier曲线参数方程为

C(t)=(1-t)2Ci-1+2t(1-t)Ci+t2Ci+1,

0≤t≤1 。

(6)

式中：t为参数；Ci-1和Ci+1分别为二次Bezier曲线的起点和终点。将Ci-1和Ci+1用所测得的探测点Pi和Pi+1代替，二次Bezier曲线参数方程可变形为

Ch(t)=(1-t)2Ph,i+2t(1-t)Ch,i+t2Ph,i+1,

0≤t≤1。

(7)

式(7)写成矩阵形式为

0≤t≤1 。

(8)

在相邻探测点Ph,i-1和Ph,i间选取一个控制点Ch,i-1，由Ph,i-1,Ch,i-1,Ph,i确定一段曲线Qh,i-1；同理，可以确定另一段曲线Qh,i。如果曲线Qh,i-1在Ph,i点处切线方向与直线Ch,i-1Ph,i一致，曲线Qh,i在Ph,i点处切线方向与直线Ph,iCh,i一致，那么Ch,i-1,Ph,i,Ch,i3点共线，即可实现曲线Qh,i-1和Qh,i在探测点Ph,i处光滑拼接，如图4所示。

图4 曲线拼接Fig.4 Curve stitching

y=mh,ix+nh,i。

(9)

(10)

同理，可以求出探测点Ph,i+1处切线Th,i+1的方程系数mh,i+1和常数nh,i+1,即

(11)

计算相邻2个探测点的切线交点，即可以求出相邻2个探测点之间控制点的具体坐标，如图5所示。

图5 控制点位置示意图Fig.5 Schematic diagram of control points

过探测点Ph,i的切线Th,i和过探测点Ph,i+1的切线Th,i+1的交点视为控制点Ch,i，其控制点Ch,i的坐标设为(xch,i,ych,i,zch,i)，即可以表示为

(12)

式中kh,i为过控制点Ch,i的切线斜率。根据同一水平断面上相邻的2个探测点可以确定一段Bezier曲线Qh,i，从而形成一段圆弧，将同一水平断面上的n段圆弧首尾连接，即可形成地下空区岩壁的水平断面轮廓。

4.3 纵向轮廓的确定

在形成了空区岩壁的水平断面轮廓曲线之后，根据计算机图形学原理，要获得空区的立体轮廓图形，还必须沿钻孔深度z方向对空区轮廓进行插值拟合。在三维坐标系中，探测点Ph,i在z轴上的深度h变化来自于深度绞车下放孔内探头，深度绞车测量下放电缆的长度h即为探测点Ph,i对应的深度。为了获取较为精确的探测数据，深度绞车下放的速度通常较慢，即深度方向上相邻2个水平断面的前后2次测量时间间隔不大，在短时间内，将孔内探头视为作垂直匀速运动。因此，在纵向轮廓的确定可以采用线性插值，采用线性插值拟合空区岩壁的纵向轮廓曲线能够高效率地生成空区的立体轮廓。

设前后2个时刻孔内探头的水平扫描断面深度位置分别为h(ti)和h(ti+1)，确定的水平断面曲线上微分的任意一点记为δ，2个相邻水平断面上对应同一纵向上的两点坐标分别记为(xh(ti),δ,yh(ti), δ,zh(ti), δ)和(xh(ti+1), δ,yh(ti+1), δ,zh(ti+1), δ),则对任一两相邻水平断面纵向上的中间点Mh(t)，坐标记作(xh(t), δ,yh(t), δ,zh(t), δ)，可以用如下坐标关系式表示：

(13)

其中t∈[ti,ti+1]。

4.4 程序实现

MatLab是以复数矩阵为基本单元的程序设计语言，具有强大的矩阵处理和绘图功能，用它实现曲线拟合和立体图形显示较为简单、高效。根据空区水平断面和纵向的曲线拟合方法，本文采用MatLab编写基于孔内超声扫描技术的空区立体轮廓生成程序，程序框图如图6所示。首先，读取孔内探头获取的探测数据，包括扫描点的测距值、方位信息以及所处深度，形成扫描点的柱坐标集合，根据关系式(1)确定平均值，选取合适的阈值，判断采样值是否为有效采样值，若无效，进行数据平滑处理，然后根据关系式(式(10)、式(11)、式(12))计算出控制点的坐标，选取合适的采样间隔，生成水平断面轮廓曲线，最后，根据关系式(13)计算出相邻水平断面轮廓上的中间点坐标，然后连接各数据点，实现纵向断面的轮廓拟合，将结果写入数据文件，形成空区立体轮廓。

图6 程序框图Fig.6 Block diagram of software

5 实例分析

为了验证本方法的可行性和准确性，根据常规地下空区的形态特征，设定若干探测数据，且数据在一定范围内波动，具有随机性，设空区位于地下深度11.5～13.5 m处，水平断面的每圈扫描点数为36个数据点，扫描点间隔角度为10°，纵向下放间隔为0.2 m，部分探测数据如表1所示。

表1 部分扫描初始数据Table 1 Part of initial scanning data

5.1 数据处理

首先，对36组数据分别进行预处理可以计算出各水平断面采集到的前3个数据点的有效值分别为：r11.5,1=r11.5，2=r11.5,3=1.16 m；r11.7,1=r11.7,2=r11.7,3=1.37 m；…；r13.2,1=r13.2,2=r13.2,3=2.36 m；r13.5,1=r13.5,2=r13.5,3=2.36 m；同时，根据关系式(1)计算出各点的平均距离，并选取阈值Nmin为0.3，Nmax为1.7，根据判断条件式(2)，对36组数据进行比较判断，筛除不满足关系式的数据点，并进行数据平滑处理，确定有效探测数据，部分数据如表2所示。

表2 数据预处理后的有效探测值Table 2 Effective detection values after data preprocessing

5.2 轮廓生成

在对扫描数据进行预处理之后，建立坐标系，根据水平断面曲线确定方法，形成各水平断面的轮廓曲线，如图7(a)所示。在形成各水平断面的轮廓曲线后，叠加深度数据，根据纵向轮廓确定方法，采用线性插值，在相同方位上取点，依次连接相邻水平断面的曲线，最终拟合出空区的立体轮廓图，绘制出的空区岩壁的立体轮廓如图7(b)所示。

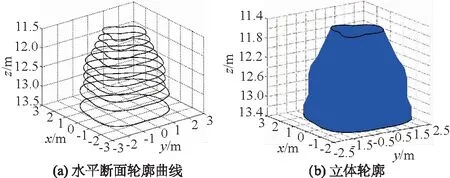
图7 水平断面轮廓曲线和立体轮廓Fig.7 Contours of horizontal sections and three-dimensional view

5.3 结果对比

目前较为常规的拟合方法为最小二乘法轮廓拟合，其拟合轮廓为圆形，采用最小二乘法将表2中的有效探测值进行立体轮廓拟合，其结果如图8所示。采用本方法进行空区的立体轮廓拟合，其结果如图9所示。

图8 最小二乘法立体轮廓拟合图Fig.8 Fitting of the three-dimensional contour by least squares method for stereo contour fitting

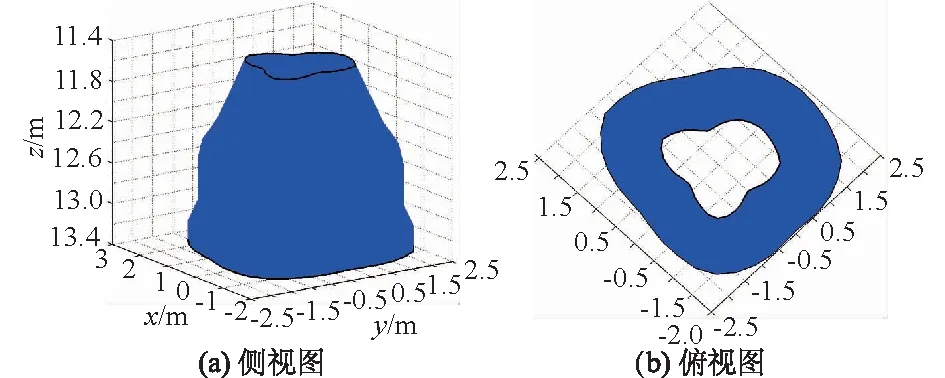
图9 空区立体轮廓确定法拟合图Fig.9 Fitting of the three-dimensional contour by the present method

图10 三角剖分立体轮廓Fig.10 Triangulation of the three-dimensional contour map

从2种方法的拟合结果可以看出，采用最小二乘法进行轮廓拟合，拟合曲线不能通过所有测量坐标点，且轮廓曲线为圆形，在实际情况下，空区的水平断面通常为非圆形，采用最小二乘法不能正确反映出空区的实际形状，存在较大误差。

此外，常规的三角剖分法能够将离散的点云生成空区的立体轮廓，孔内空区是一个较为封闭的区域，空区的轮廓曲线处于闭合状态，平面投影存在重叠现象，采用三角剖分法需要加入分割面才能形成封闭空区的轮廓，计算较为复杂；三角剖分法是根据离散点生成的轮廓，由大量平面三角形组成空区的立体轮廓面，改变局部散点数据值，将产生较大变形，如图10所示。

而采用本方法进行空区的轮廓拟合，首先需要进行数据预处理，能够有效剔除部分无效数据，且拟合曲线经过每一个有效测量点，能够更加真实地反映出空区的实际形态，能够避免由累计误差引起的轮廓失真。同时，将本方法形成的立体轮廓进行图像映射(图11)，能够更加形象地展示空区的各种地质特征，为后期的地下工程研究提供重要的数据支撑。

图11 空区纹理映射图Fig．11 Texturemapping

6 结 论

本文结合孔内超声扫描技术，首先提出了针对超声扫描数据的预处理方法，判断有效数据点，并平滑处理非有效探测点，实现超声数据的有效筛选。其次，引入二次Bezier曲线，并提出了适用于空区水平断面拟合特点的曲线拟合方法，使Bezier曲线能够通过每一个有效测量点，实现空区轮廓的高精度拟合；水平断面轮廓拟合之后，叠加深度信息，采用线性插值完成空区轮廓的纵向插值拟合，实现空区的立体轮廓确定，并通过MatLab软件进行数据的计算和图像生成。最后，通过具体数据进行分析，并与其他拟合方法进行对比。结果表明：①孔内超声扫描系统能够为空区建模提供有效数据；②改进的Bezier曲线能够适用于空区水平断面轮廓的拟合；③线性插值拟合能够快速实现空区轮廓的纵向拟合；④基于超声扫描的空区轮廓拟合方法具有可行性和准确性。

[1] 国家安全生产监督管理总局研究中心.我国矿产资源开采现状调查[R].北京：国家安全生产监督管理总局研究中心，2005.

[2] 过 江,古德生,罗周全.金属矿山采空区3D激光探测新技术[J].矿冶工程,2006,26(5):16-19.

[3] 蒋 俊.岩溶及采空区塌陷的地质灾害研究[D].长沙：中南大学,2008.

[4] 闫小兵，周永胜，申 飞.TSP203在溶洞探测中的应用[J].工程地球物理学报,2007,4(6):589-595.

[5] 杨春和，梁卫国，魏东吼，等.中国盐岩能源地下储存可行性研究[J].岩石力学与工程学报，2005，24(24)：4409-4417.

[6] 吴 铠.用最小二乘法拟合圆应用于隧道钢模台车尺寸检查[J].四川水泥，2004，(11)：132，151.

[7] 田社平，张守愚，李定学，等.平面圆圆心及半径的最小二乘法拟合[J].实用测试技术，1995，(5):23-25.

[8] 徐国旺，廖明潮.拟合圆的几种方法[J].武汉工业学院学报，2002，(4)：104-106.

[9] 刘书华，文良起，翟建武.非圆曲线的最小二乘法拟合法[J].新技术新工艺，2001，(7)：12-14.

[10] 许静雅.参数曲线、曲面的拟合及其拼接[J].华南工学院学报(自然科学版),1987,15(3):117-121.