纯棉色纺纱配色中的Stearns-Noechel模型参数优化

白 婧， 杨 柳， 张 毅， 张瑞云， 马颜雪， 俞建勇, 程隆棣

(1. 东华大学 纺织学院， 上海 201620； 2. 浙江省常山纺织有限责任公司， 浙江 衢州 324200)

色纺纱是先将纤维进行染色，然后选用2种或者2种以上不同颜色的纤维，按照一定质量比纺制而成的纱线，具有独特的混色效果[1]。色纺是纺织行业中的朝阳产业，色纺纱在纺织领域的应用越来越广泛，需求量也日益增加，同时棉纤维作为纺织工业中的主要原料，对其色纺纱配色进行研究更具价值。

目前大多数色纺企业仍然采用人工配色，工作量大，耗时，成本较高，而且主观性强，配色完全依靠人眼观察，易受配色人员的心理状态、外界环境、个人经验及对颜色的敏感度等因素影响，配色效果缺乏统一的衡量标准，配色的准确度不高，再现性差。色纺纱的计算机测配色主要是利用测色软件在特定光源下测试一系列常用的单色纱线，获得相应的颜色色度值、反射率等参数指标，作为后续配色的基础数据库。根据纤维种类，选择合适的颜色匹配模型，通过实验确定模型中的待定参数，设计计算机配色系统，获得标准样所对应的配方及预测样与标准样之间的色差值。

色纺纱所用的纤维种类主要有棉、羊毛以及涤纶等，针对计算机配色的代表性模型主要有Stearns-Noechel模型、Friele模型和 Kubelka-Munk模型，其中，Stearns-Noechel模型的预测准确度相对较高[2]。国内不少学者已经就Stearns-Noechel模型做了很多研究，但主要集中在染色毛条及化学纤维的运用上，而对于有色棉纱的研究较少，同时模型的配色准确度有待提高，因此，本文在Stearns-Noechel模型基础上，以纯棉色纺纱配色为研究对象，结合数理统计方法，对模型的待定参数进行优化分析，进而实现模型的精准配色。

1 Stearns-Noechel模型简介

1944年，Stearns和Noechel[3]在Duntley[4]提出的有色纤维反射率加和混色模型的基础上，利用黑白两色羊毛纤维进行混色实验，假设式(1)成立，基于实验结果提出了经验式(2)，通常称该经验公式为Stearns-Noechel模型。

(1)

(2)

式中：f[]表示波长为λ时反射率的中间函数；Rblend(λ)表示波长为λ时色纤维混色样的总体反射率；Ri(λ)表示波长为λ时第i组分单色纤维的反射率；Xi表示第i组分单色纤维所占的比例，∑Xi=1；b是待定参数，其值取决于纤维的种类以及纤维的物理形态，需要通过具体的实验来确定，表1示出目前对最优b值做的研究。

由表中数据可看出：关于棉纤维，文献[9]与文献[2]推荐的最优b值的差异较大，并且研究都只是针对两色混合效果，而实际生产中三色、四色混合的现象也比较多；另外，对于棉色纤维的单纱结构的Stearns-Noechel模型配色研究，目前还少有相关报道，因此，为充分探究Stearns-Noechel模型在棉纤维配色中的应用，仍然要通过实验，对参数b值的具体取值进行研究。

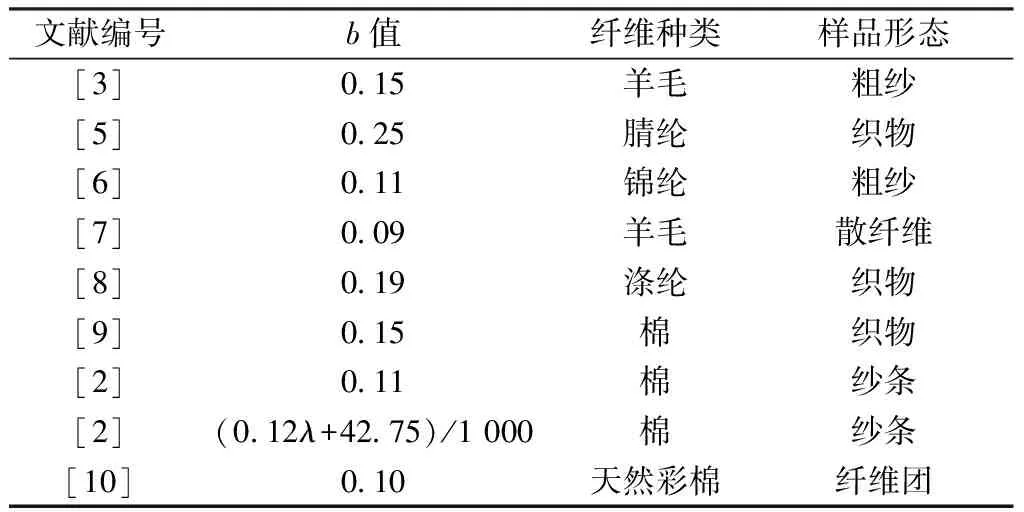
表1 不同文献选定的纤维参数b值Tab.1 Values of b for different fibers in different references

2 光谱配色算法

2.1 全光谱配色算法

理想状态下的全光谱配色是在任意波长处，匹配样与标准样的光谱反射率值完全相等，即

Rm,λ=Rs,λ

(3)

式中：Rm,λ、Rs,λ分别代表波长为λ时匹配样与标准样的反射率，由式(2)、(3)可知，

f(Rm,λ)=f(Rs,λ)

(4)

在实际计算中，等式(4)的左右两端并不完全相等，即匹配样的反射率值与标准样的反射率值有一定的偏差，由此引入最小二乘法，使得偏差达到最小。最小二乘法得到的配方比例之和通常不等于1，所以再利用归一法将比例之和限定为1，以满足∑Xi=1。

2.2 色差公式

评价色纺纱品质优良与否的指标是色差，色差量化可使颜色的差异有数值上的衡量标准。通过Stearns-Noechel模型可得到预测配方及匹配样的反射率值，而匹配样是否满足要求，可通过匹配样与标准样之间的色差进行衡量，色差越小，说明模型的精度越高，配方的准确度越高，实用性越强。CMC(l∶c)色差公式具有很好的目视一致性，应用广泛，是CIE推荐使用的标准色差公式之一[11]，也是纺织行业的ISO标准，因此本文采用CMC(2∶1)公式。

3 实验部分

3.1 实验材料

选用青(C)、品红(M)、黄(Y)、黑(K)、白(W)5种基准色的棉纤维，其色度参数如表2所示，光谱反射率如图1所示。

表2 5种颜色棉纤维的CIELab色度参数值Tab.2 CIELab values of five colored cotton fibers

注：L*为明度；a*为红-绿色调；b*为黄-蓝色调；c*为饱和度；h*为色相角。

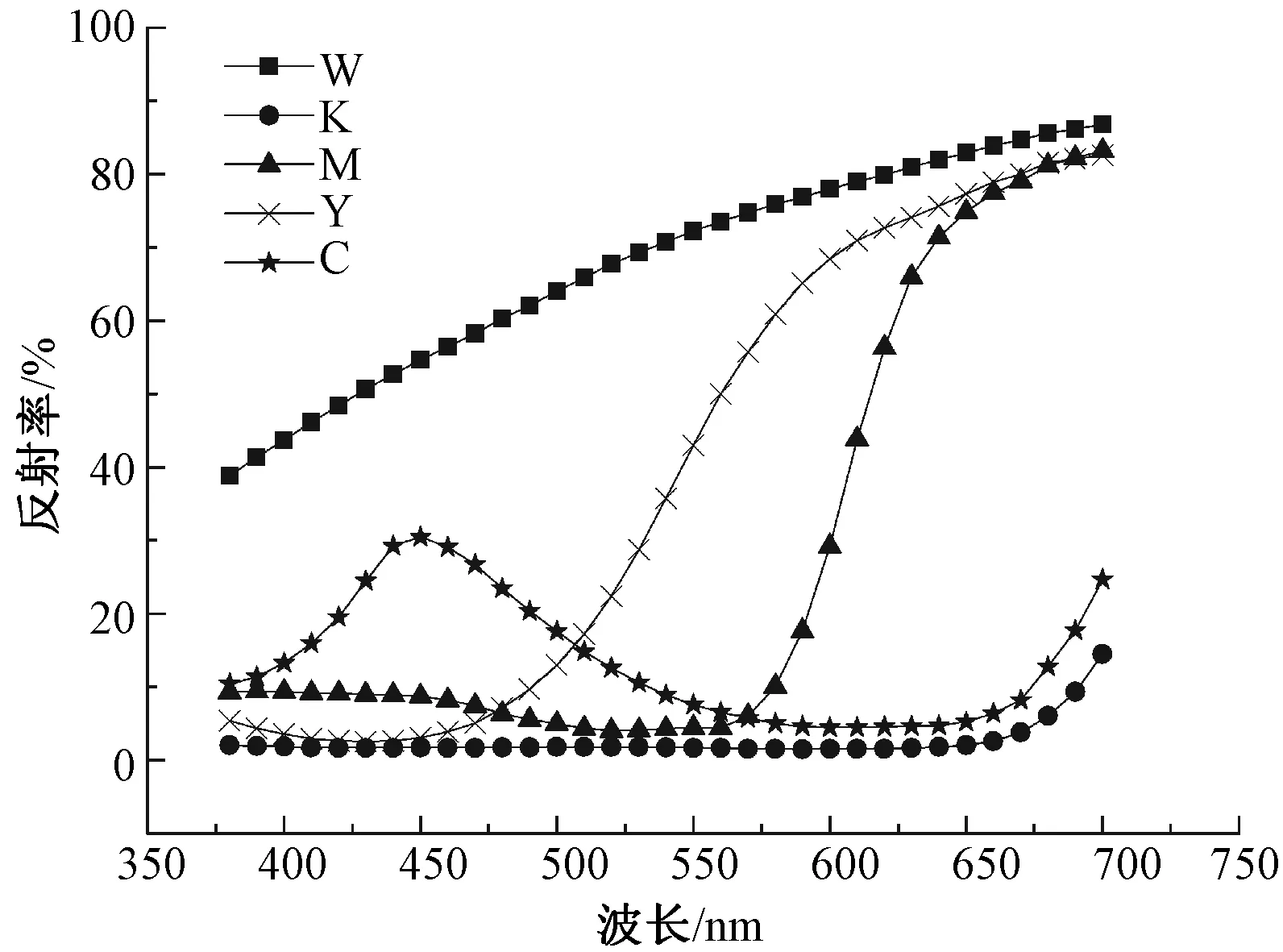
图1 5种单色棉纤维的反射率值Fig.1 Reflectance values of five colored cotton fibers

3.2 样品的制备工艺

选取青、品红、黄、黑、白中的部分基准色纤维，以两色、三色、四色混合的形式制备252个样品，每个样品的质量比例以100组分为标准，其中两色混合表示为AB，AB的组合分别为黑与白、品红与黄、品红与青、黄与青，每种组合方式制作9个不同质量比例的样品，间隔为10组分，两色共制备36个样，具体的配比见表3。三色采用青、品红、黄进行混合，间隔为10组分，共制备36个样，具体的配比见表4。四色混合即上述三色中加入白色或者黑色，白色在样品总质量所占组分分别为20、40、60，同时保持青、品红、黄之间的比例关系与三色混合的比例一致，青、品红、黄、白四色混合共制作108个样品。加入黑色与加入白色的情况相同，黑色在样品总质量所占组分分别为20、40，共计72个样品。以白色占20组分的四色混合进行说明，具体配比见表5。

表3 2种颜色纤维的质量混合比例Tab.3 Blending mass ratio of two colored fibers

表4 3种颜色纤维的质量混合比例Tab.4 Blending mass ratio of three colored fibers

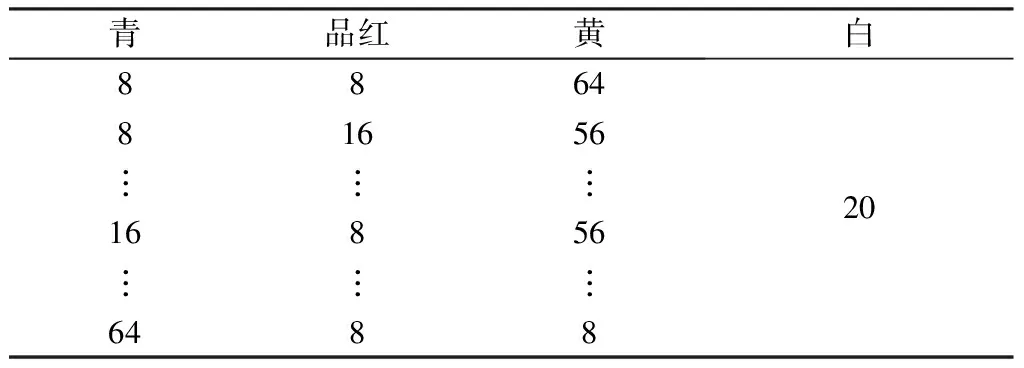
表5 4种颜色纤维的质量混合比例Tab.5 Blending mass ratio of four colored fibers

采用LS600电子天平称量每个样品的纤维，总质量为50 g，将混合后的纤维在A186F型梳棉机上梳理3次，以保证不同颜色的棉纤维可均匀混合，采用A272F型并条机进行1道并条，并由A454G型粗纱机制成粗纱，细纱工序采用A513F型环锭细纱机，纺成19.5 tex的细纱，用Y108型纱线色卡机将纱线制成色卡，卷绕的规格为40 mm×40 mm，卷绕4层，以保证不透光。

3.3 测试方法

采用Datacolor 650型台式分光光度测色仪进行测试。仪器经预热及校正后，在D65标准光源和10°视场条件下测量，选择测色孔径为30 mm的大孔径，以保证测色结果相对比较准确，在色卡样品的不同位置测量5次，取平均值，波长范围为380～700 nm，每间隔10 nm取1个点，可得到33个不同波长下的光谱反射率值。

4 模型参数b的最优值确定

运用Stearns-Noechel模型进行计算机配色的前提是确定模型中的待定参数值b，因此，如何确定最优b值成为模型运用的关键环节，希望最优b值在任意颜色和任意比例组合时，都能够使匹配样的反射率值Rm,λ与仪器实测的反射率值Rs,λ之间的色差达到最小。

4.1 参数b值的传统确定方法

由式(1)、(2)可知，由Stearns-Noechel模型得到的匹配样的反射率Rm,λ与参数b值的大小有关，由此，参数b值改变，模型推导所得的匹配样反射率值Rm,λ也改变，匹配样的反射率值与仪器实测的反射率值之间的色差也随之改变。匹配样的反射率Rm,λ与样品组分之间的关系满足如下等式。式中：R1,λ，R2,λ，…，Rn,λ为样品中各单色纤维在某波长下的反射率值；x1，x2，…，xn为样品中各单色纤维所占的质量比；n为样品中所含色纤维的种类。

对于不同种类的纤维，学者们推荐的参数b的取值范围均为0～1。由于参数b最优值的选取运算量比较大，运用MatLab软件进行编程循环计算，b的取值从0.001到1，间隔设为0.000 1。实验选取252个混色样品，利用SPSS软件进行统计分析，各自对应的最优b值的频数分布如图2所示，所有b值及对应最小CMC色差的箱图如图3、4所示。

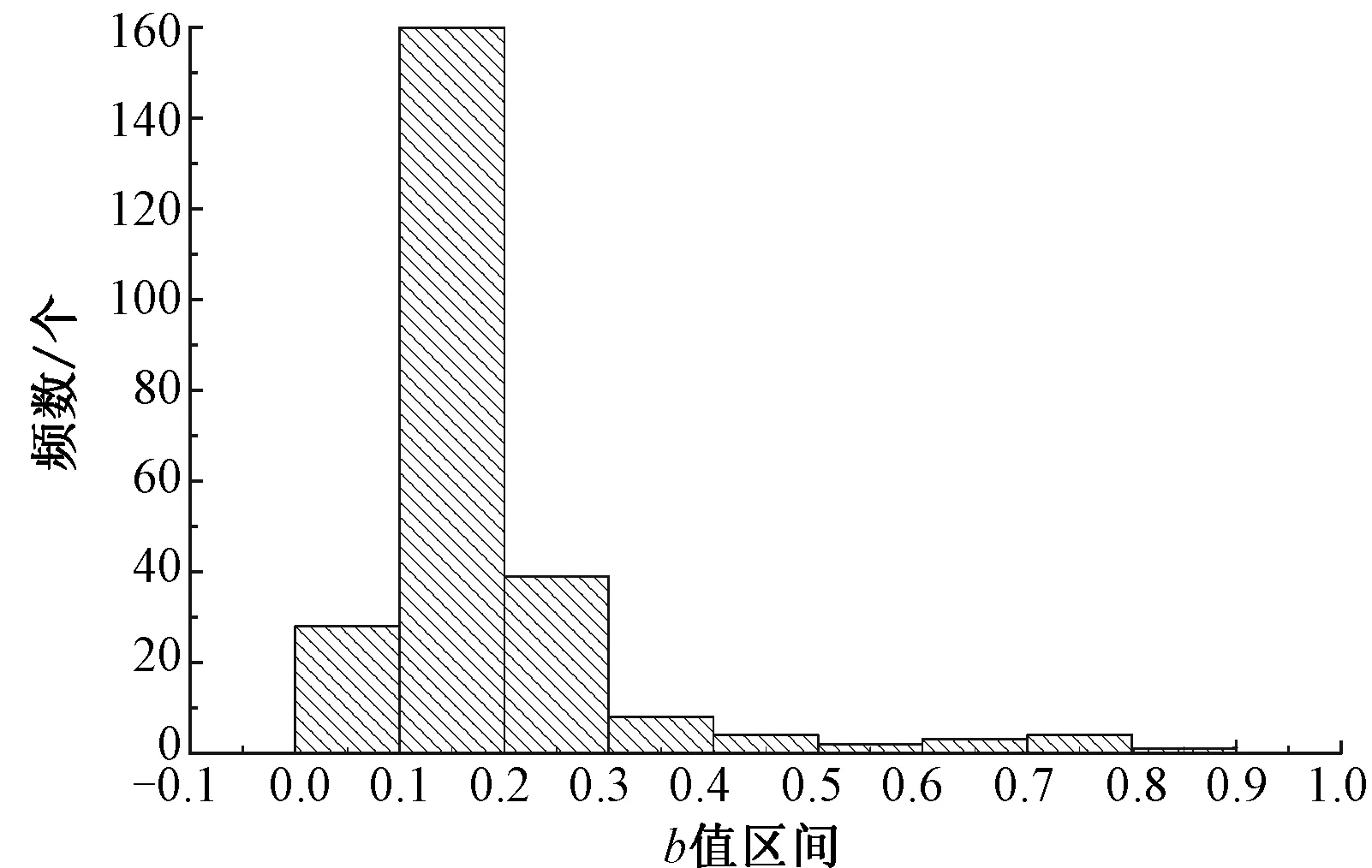
图2 252个混色样品对应最优b值的频数分布图Fig.2 Frequency distribution of 252 blended samples corresponding to optimal b values

图3 252个混色样品对应最优b值的箱图Fig.3 Box chart of 252 blended samples corresponding to optimal b values

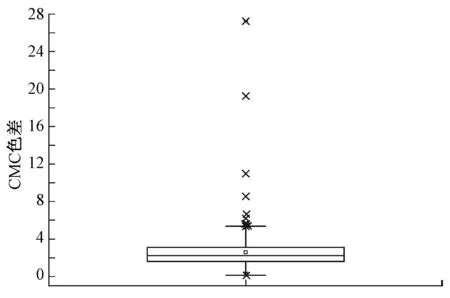
图4 252个混色样品最小色差的箱图Fig.4 Box chart of smallest color difference of 252 blended samples

从图2看出，b值的分布范围较广，但主要集中在0～0.3之间，且根据已有研究发现，参数b的最优常数值均在0.3以下。从图3看出，252个b值中存在部分异常值，应予以剔除，图4中有部分样品的CMC色差过大，属于异常值，应该剔除。综合上述分析，剔除参数b大于0.3的值，同时剔除色差大于5对应的b值，再进行统计，结果如图5、6所示。

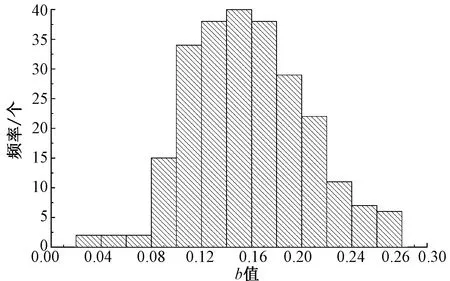
图5 剔除异常值后的最优b值频数分布图Fig.5 Frequency distribution of optimal b values after removing outliers

图6 剔除异常值后的最优b值箱图Fig.6 Box chart of optimal b values after removing outliers

从图5看出，b值在0～0.3之间基本成正态分布，且在0.15左右的频数较大。中位数反映数据的集中趋势，从图6看出，箱图的中位数是0.154 2。由此，本文依照Stearns-Noechel模型中参数b的传统确定方法，得到的最优b值为0.154 2。

4.2 参数b与波长的关系

纤维呈现颜色的根本原因是其对光的选择性吸收，光线照射在纤维上，纤维会选择性地吸收某一波长的光，而将其余波长的光反射出来，因此，吸收、散射以及颜色都与波长相关。由式(2)可看出，b是唯一的待定参数，而波长是式(2)中的可变值，所以推测b值也极有可能与波长相关。同时，文献[2]中采用14种颜色的棉纤维，以不同组合方式制成234个混合样，混合样以生条的形式进行研究，证明参数b与波长存在一定线性关系。

本文采用C、M、Y、K、W 5种颜色的棉纤维，以不同组合方式不同颜色比例进行混合，获得252个混合样，并制成19.5 tex的细纱。结合式(1)、(2)，运用MatLab软件，计算不同波长(380～700 nm，间隔为10 nm)下的常数b值，图7示出各波长下b值分布的散点分布。表6示出各波长下b值的中位数。

图7 不同波长下参数b的散点分布图Fig.7 Scatter distribution of parameter b at different wavelengths

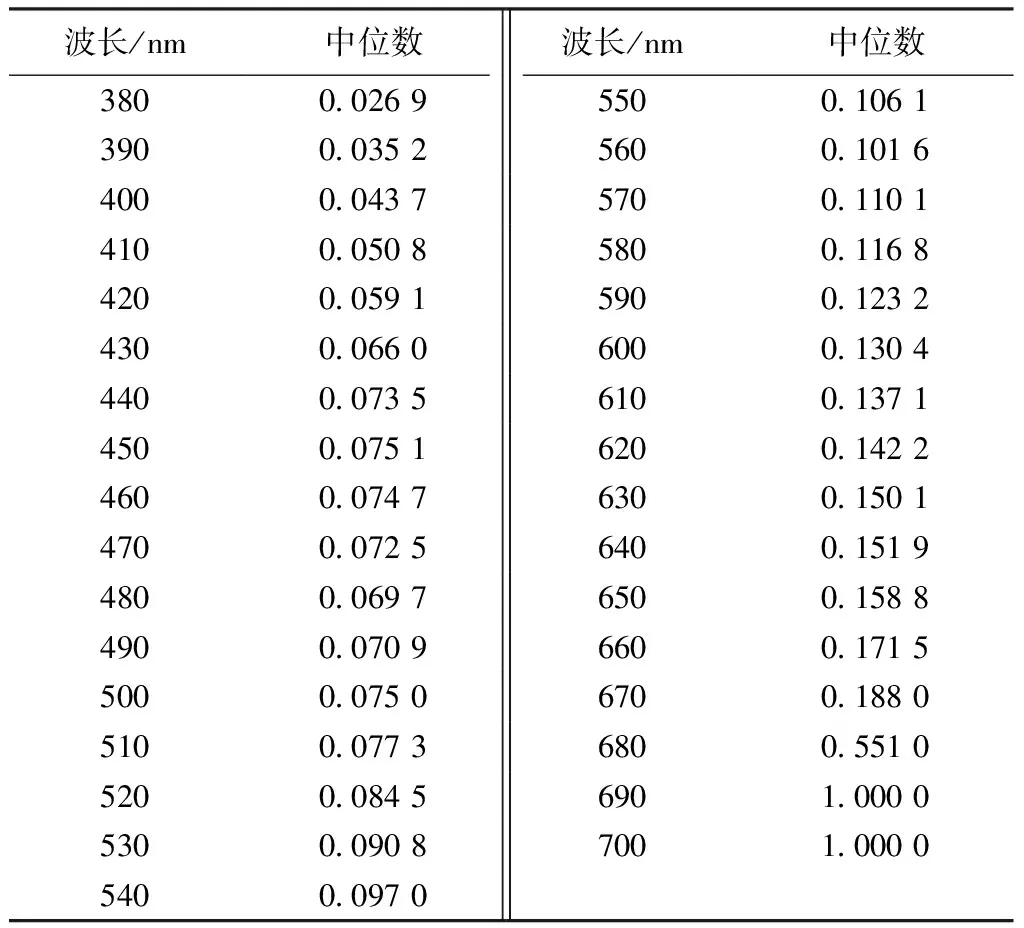
波长/nm中位数波长/nm中位数380002695500106139000352560010164000043757001101410005085800116842000591590012324300066060001304440007356100137145000751620014224600074763001501470007256400151948000697650015884900070966001715500007506700188051000773680055105200084569010000530009087001000054000970

从图7可看出，b值在0～0.3之间分布得比较集中，从整体趋势来看，随着波长的增大，b值集中的区域越来越大，当波长大于670 nm时，b值的分布更加离散，而且由表6可知，波长大于670 nm，b值的中位数明显异于其他位置，因此，选取380～670 nm之间的波长， 运用SPSS软件，经线性回归拟合出b值与波长之间的线性方程。

b=(0.45λ-137.98)/1 000

结果表明，b值与波长之间的显著性系数P小于0.01(P值小于0.05说明具有显著性意义)，Pearson相关系数R为0.976，说明参数b与波长之间线性相关显著。

4.3 参数b与样品颜色组分的关系

颜色可以分为非彩色和彩色2个大类。非彩色是指白色、各种由浅到深的灰色和黑色，它们可以形成一个非彩色系列。非彩色以外的所有颜色都属于彩色。

研究中将252个混色样品的颜色分为2类：非彩色和彩色，分别按照4.2所述的方法进行分析，各类的b值散点分布如图8、9所示。

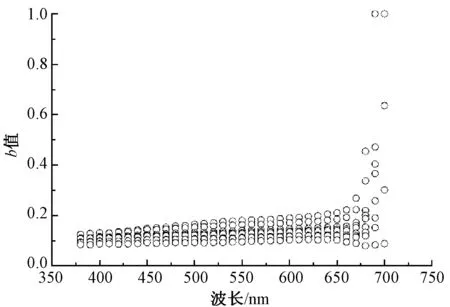
图8 不同波长下非彩色样品的b值散点图Fig.8 Scatter distribution of parameter b of non-color samples at different wavelengths

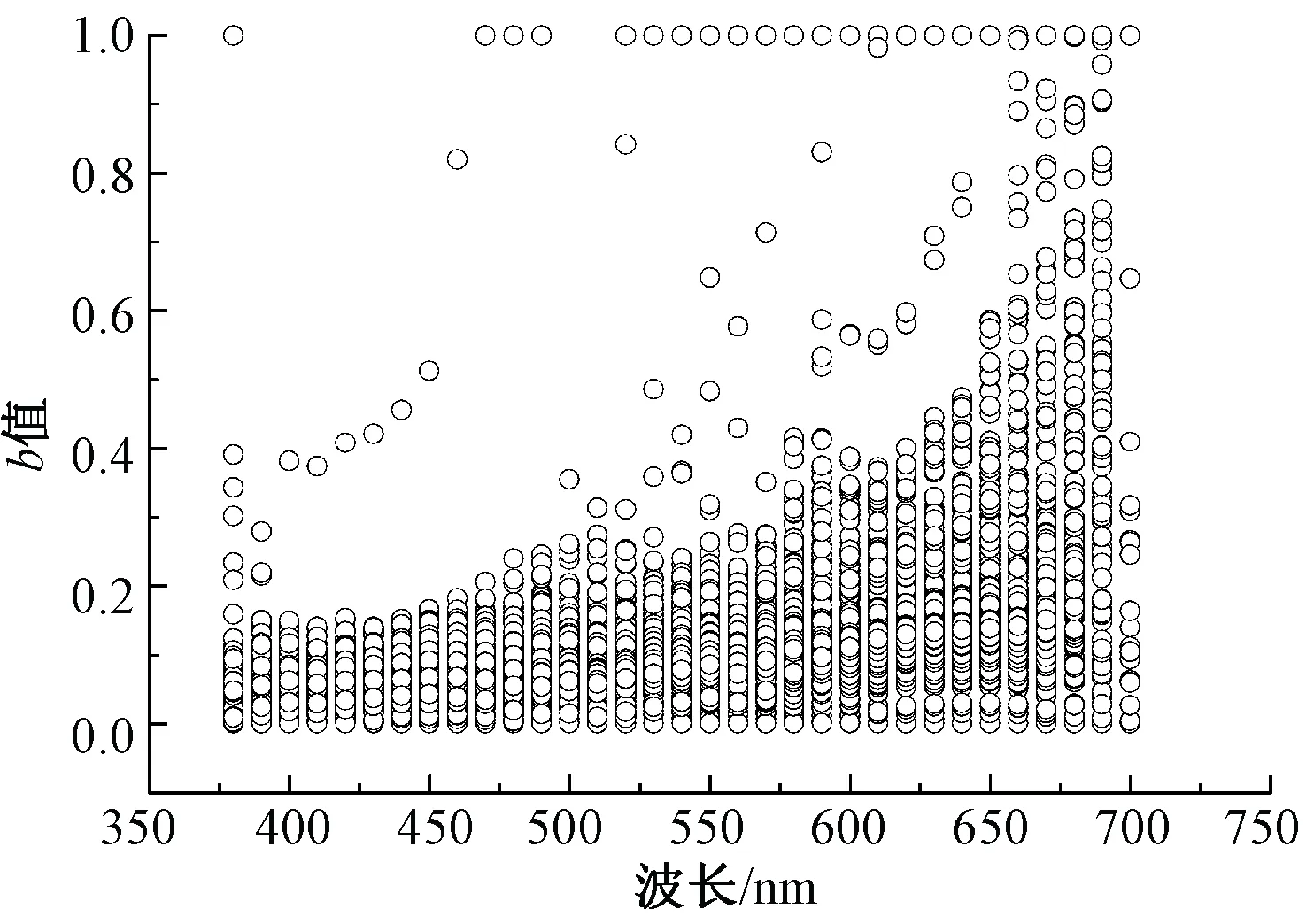
图9 不同波长下彩色样品的b值散点图Fig.9 Scatter distribution of parameter b of color samples at different wavelengths

针对非彩色和彩色样品，选取380～670 nm之间的波长，间隔为10 nm，统计每个波长下b值的中位数，运用SPSS软件，经线性回归拟合出b值与波长之间的线性方程。

对于非彩色样品，b值与波长之间的线性方程为b=(0.13λ+58.87)/1 000，显著性系数P小于0.01，Pearson相关系数R为0.986，说明参数b与波长之间线性相关性显著；对于彩色样品，b值与波长之间的线性方程为b=(0.46λ-144.61)/1 000，显著性系数P小于0.01，Pearson相关系数R为0.975，说明参数b与波长之间具有显著的线性相关性。

5 结果与讨论

在对参数b值的研究中，将所得到的b值分别记为b1=0.154 2，b2=(0.45λ-137.98)/1 000，非彩色系的b31=(0.13λ+58.87)/1 000，彩色系的b32=(0.46λ-144.61)/1 000，将其代入式(2)即可得到新的修正模型。为能够清晰地分析与解释，将以上b值所对应的修正模型分别称为B1模型、B2模型和B3模型，其表达式分别为：

f[R(λ)]=

结合式(1)、(2)以及CMC色差公式，运用MatLab软件，计算出各混色样的预测比例及色差。

图10示出以黑白质量比为60∶40的样品为例，比较样品的实测反射率值与各模型所得的预测反射率值之间的差异。可知，只有B3模型预测的反射率与实际反射率最吻合。

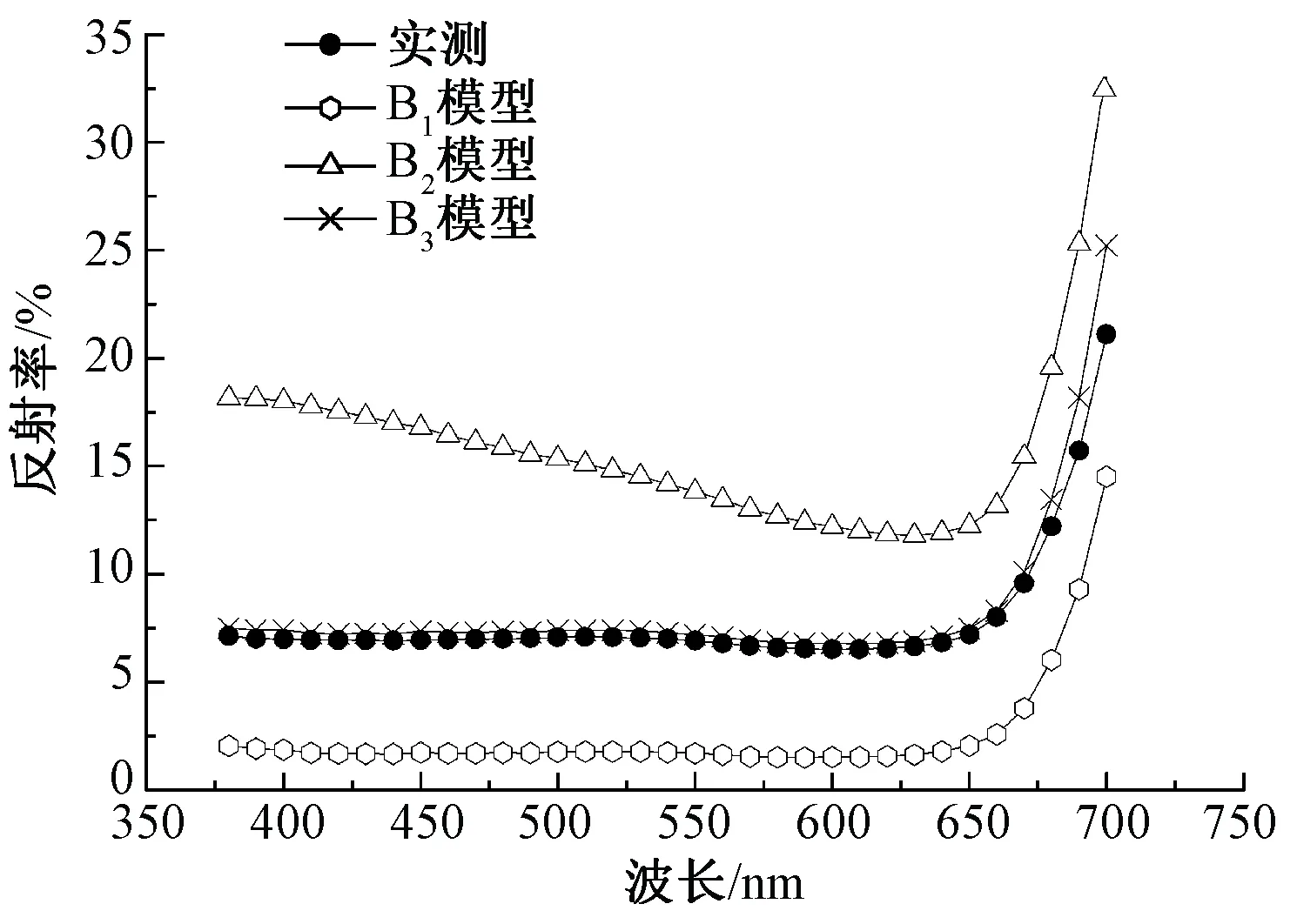
图10 样品实测与模型预测反射率对比Fig.10 Comparison of sample measured with model predicted reflectances

表7示出各个模型所对应的预测样与标样之间的平均色差。可知，在预测非彩色系列的样品时，B1模型和B2模型的平均色差很大，不能很好地用于纯棉色纺纱的配色，而B3模型的平均色差只有1.24，效果最好。在预测彩色系列样品时，B2模型与B3模型相差不大，但是从总体色差来看，B3模型的平均色差最小，预测效果最好，说明B3模型更适用于棉色纤维的颜色预测，即将非彩色与彩色系列分开求参数b时预测效果更佳。

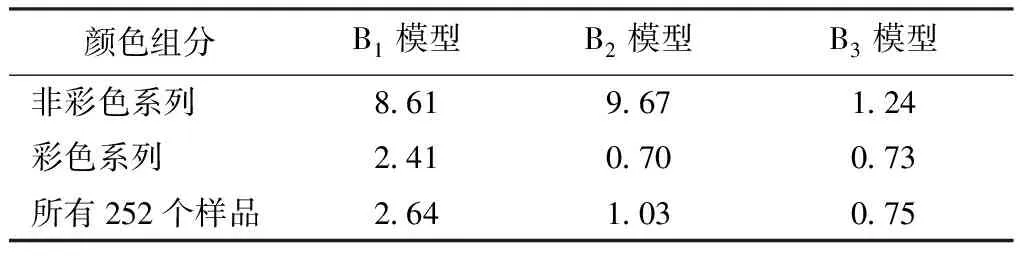
表7 各模型平均CMC色差的对比Tab.7 Comparison of average color differences of models

B3模型的预测效果优于另外2个模型，其原因在于确定B3模型的参数时，不仅考虑了波长的因素，也将样品的颜色按照彩色与非彩色2个系列分开研究。根据理论分析，非彩色只有明度，没有饱和度与色调，而彩色样品包含颜色的3个属性，因此，在模型参数的确定中，非彩色与彩色样品的参数值会有较大的不同。进一步分析研究表明，分非彩色与彩色系列研究，模型预测配方更加准确，色差更小，用于配色时更有优势。

6 结 论

本文主要研究纯棉色纺纱配色，采用青、品红、黄、黑、白5种颜色的棉纤维，制作252个不同组分不同比例的纱线样品，以Stearns-Noechel模型为切入点，结合数理统计分析软件，对模型中的待定参数b值进行研究，运用传统取值方法以及b值与波长、颜色组分之间的关系，分别建立了B1、B2和B33个新的修正模型。得到的主要结论如下：

1)B1、B2模型虽然可实现配方预测，但用于非彩色系列样品的预测时，色差相对较大；

2)B3模型用于样品预测时，总平均色差最小，因此将样品分为非彩色和彩色系列，并考虑待定参数值与波长的关系，这样所得到的修正模型预测配方更精确，色差更小，可满足棉纤维配色的要求。

[1] 钱爱芬.色纺纱产品特点及调配色原理[J].棉纺织技术,2010,38(11)：66-68．

QIAN Aifen. Colored spun yarn characteristic and colormixing and matching principle[J]. Cotton Textile Technology,2010,38(11):66-68.

[2] PHILIPS Invernizzi B, DUPONT D, JOLLY Desodt A M, et al. Color formulation by fiber blending using the Stearns-Noechel model[J]. Color Research and Application, 2002, 27(2): 100-107.

[3] STEARNS E I, NOECHEL F. Spectrophotometric prediction of color of wool blends [J]. American Dyestuff Reporter,1944,33(9):177-180.

[4] DUNTLEY S Q. The prediction and control of colored fiber blends by optical mixing [J]. American Dyestuff Reporter, 1941, 30: 689-700.

[5] DAVIDSON H R, TAYLOR M. Prediction of the color of fiber blends[J]. Journal of the Optical Society of America, 1965, 55 (1):96-100.

[6] BURLONE D A. Theoretical and practical aspects of selected fiber-blend color formulation functions[J]. Color Research and Application,1984,9(4):213-219.

[7] FRIELE L F C. The application of colour measurement in relation to fiber-blending [J]. Journal of the Textile Institute Proceedings,1952,43:604-611.

[8] ASPLAND J R, ZHOU M．Influence of blending on color appearance of black and whiter fiber blends[J]. Textile Chemist and Colorist and American Dyestuff Reporter, 2000, 32 (10): 47-51.

[9] 许佳艳.涤棉双组分纤维混色计算机辅助配色的研究[D].杭州:浙江理工大学,2013:22-23.

XU Jiayan. The study on computer aid matching for colored fiber belnds of polyester and cotton[D].Hangzhou: Zhejiang Sci-Tech University, 2013:22-23.

[10] 王泉,姚佳,李艳清,等.Stearns-Noechel模型在天然彩色棉混色中的应用[J]. 纺织学报, 2016, 37(1):93-97.

WANG Quan, YAO Jia, LI Yanqing, et al. Application of Stearns-Noechel model on color blending of naturally colored cotton[J]. Journal of Textile Research, 2016, 37 (1):93-97.

[11] CLARKE F J J, MCDONALD R, RIGG B. Modification to the JPC79 colour-difference formula[J]. Journal of the Society of Dyers and Colourists, 1984, 100(4): 128-132.