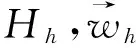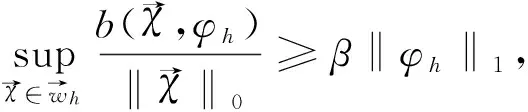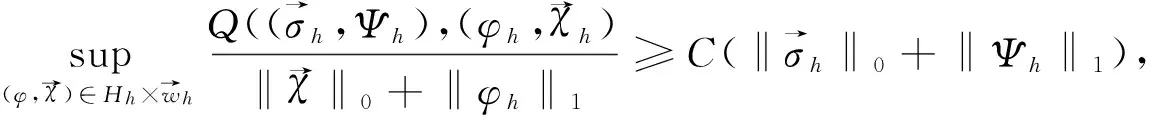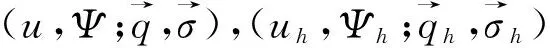四阶椭圆方程一个新混合元模式的高精度分析
王萍莉,牛裕琪
(许昌学院 数学与统计学院,河南 许昌 461000)
众所周知, 传统混合有限元方法所涉及的两个有限元逼近空间通常要求满足LBB相容性条件,这通常不是一件容易的事.因此出现了一些不需要满足这一限制条件的混合有限元格式,如H1-Galerkin有限元方法[1],最小二乘有限元方法[2],稳定化方法[3]等.最近,[4,5]针对二阶椭圆问题给出了一种新的混合元格式,考虑了其收敛性分析,并且发现当选取的空间对满足一个简单的包含关系时,该格式自然满足LBB相容性条件,基于这一明显优势,随后该方法被用于解决其它问题[6-8],并得到了满意的收敛结果.其中,[6]基于[4,5]的工作进一步研究了二阶椭圆问题的超逼近及超收敛性质;[7,8]分别在正则网格和各向异性网格下讨论了抛物方程的混合元逼近格式,并都给出了收敛性分析.
本文考虑四阶椭圆问题的初边值问题
(1)
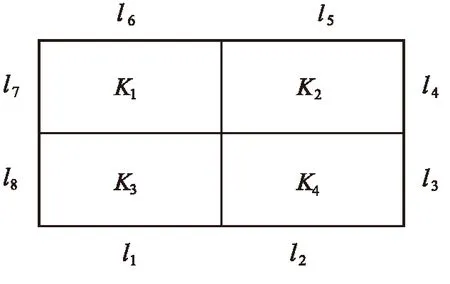
其中,Ω⊂R2是x-y平面上具有Lipschitz连续边界∂Ω的有界凸区域,0 众所周知,四阶问题具有深刻的物理背景,在许多方面具有广泛的应用,其中之一可以用于刻画弹性梁的状态,而弹性梁是现代飞机、轮船、建筑等最基本的结构之一,因而关于这类问题的研究对于理论与实际应用都具有十分重要的意义.由于四阶问题出现了高阶导数,因此其数值求解有一定的困难,其研究方法通常有有限差分方法,有限体积元方法, 有限元方法和混合有限元方法[9-11]等.其中,[9]研究了四阶椭圆和抛物问题的混合有限元方法,得到了最佳收敛阶;[10]利用扩展混合元方法给出了四阶椭圆问题的误差估计; [11]对四阶椭圆问题构造了三个C0非协调单元,并证明了一个单元是一阶收敛,另两个单元是二阶收敛. 本文的主要目的是基于[4,5]的思想,利用双线元Q11及其梯度空间Q01×Q10对四阶椭圆方程建立了一种新的混合元逼近格式.利用单元的良好性质,借助于积分恒等式技巧和插值后处理技术,导出了相应变量的超逼近性质及整体超收敛结果. 定义混合有限元空间如下 设Ihv→Ihv和分别为有限元空间Vh和上相应的插值算子,并且满足 Ih|K=IK,IKv(ai)=v(ai) 和 (2) (3) 借助文[4]-[6]对二阶椭圆问题的讨论,可知混合变分问题(3)存在唯一解. (4) (5) 为了得到超逼近,首先介绍下面引理. 由[6]可知如下引理成立. (6) 则有如下的弱强制性 (7) [12]已经证明了如下引理成立. (▽(u-Ihu),▽vh)=O(h2)|u|3‖vh‖1,u∈H3(Ω). (8) 借助于引理1,2,我们可以得到如下超逼近性质. (9) (10) (11) 借助于引理1和(11a),可得 (12) 由[6]可知,下述关系成立 ▽Ih=Πh▽. (13) (14) 由(14)式并结合a(.,.)和b(.,.)的定义, (12)可化为 (15) 注意到(14)式和引理2, 故有 (16) 结合(15)和(16)式可得 (17) 图1 大单元 (9)得证. 类似可证(10). 定理得证. 结合I2h和Π2h的性质,并利用定理1的结论则很容易得到如下的超收敛结果. 定理2 在定理1的条件下,则有 (18) (19) 证明 由定理1及I2h和Π2h的性质,可得 (18)式得证,同理可证(19)式. 注 在矩形剖分格式下,上述混合元模式能够得到相应变量的超逼近性质,关键在于文[6]中证明的(13),使得(16)式的估计可以利用双线性元的高精度结果. [1] Pain A K. An H1-Galerkin mixed finite element methods for parabolic partial differential equations [J]. SIAM journal on numerical analysis, 1998, 35(2): 721-727. [2] Yang D P.Least-squares mixed finite element methods for nonlinear parabolic problems[J]. Journal of Computational Mathematics, 2002, 20(2): 153-164. [3] Bochev P B, Dohrmann C R, Gunzburger M D. Stabilization of low-order mixed finite elements for the Stokes equations[J]. SIAM Journal on Numerical Analysis, 2006, 44(1): 82-101. [4] 陈绍春,陈红如.二阶椭圆问题新的混合元格式[J].计算数学,2010,32(2):213-218. [5] 史 峰,于佳平,李开泰.椭圆型方程的一种新型混合有限元格式[J].工程数学学报,2011,28(2):231-237. [6] 石东洋,李明浩.二阶椭圆问题一种新格式的高精度分析[J].应用数学学报,2014,27(1):45-58. [7] 李 磊,孙 萍,罗振东.抛物方程一种新混合有限元格式及误差分析[J].数学物理学报,2012,32(6):1 158-1 165. [8] 张亚东,石东洋.各向异性网格下抛物方程一个新的非协调混合元收敛性分析[J].计算数学,2013,35(2):171-180. [9] Chen Z X. Analysis of expanded mixed methods for fourth-order elliptic problems[J]. Numerical Methods for Partial Differential Equations, 1997, 13(5): 483-503. [10] Pao C V. Numerical methods for fourth‐order nonlinear elliptic boundary value problems[J]. Numerical Methods for Partial Differential Equations, 2001, 17(4): 347-368. [11] 陈红如,陈绍春.四阶椭圆问题的 非协调元[J].计算数学,2013,35(1):21-30. [12] 林 群,严宁宁.高校有限元构造与分析[M].保定:河北大学出版社,1996.1 单元构造及逼近格式
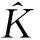

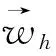
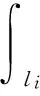
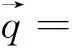
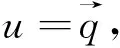
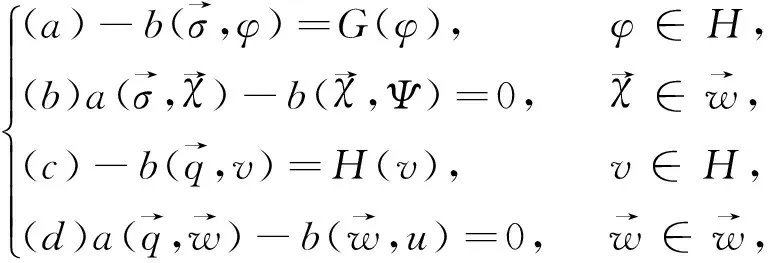
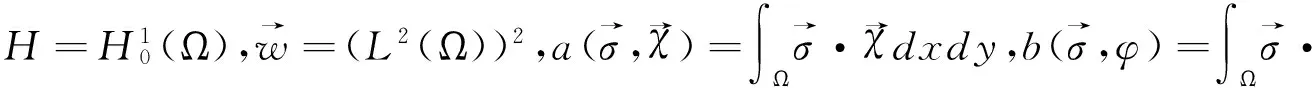
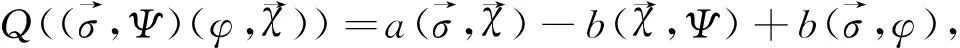
2 超逼近及超收敛分析