550 kV断路器用密封杆疲劳分析及试验研究*
高振奎,秦晓宇,马晓红,张 垒,骆常璐(河南平芝高压开关有限公司,河南 平顶山 467013)
0 引 言
高压断路器是电网系统的重要组成部分之一,保证了系统的安全运行[1]。GB-1984规定断路器进行开合万次寿命实验,在设计过程中需要对关键零部件进行疲劳寿命分析。疲劳分析开始于18世纪末,从1871年沃勒提出疲劳寿命曲线及疲劳强度极限的概念到1971年WETZAL R M基于Manson-Coffin方程,提出了局部应力应变估算疲劳寿命的方法[2-3],疲劳研究工作者对疲劳进行了多方面大量的探索。冲击载荷疲劳寿命常用的估算方法分为名义应力法和局部应力应变寿命法[4-5],但时至今日,冲击载荷作用下的疲劳损伤研究还处在较为初级的阶段,相关的理论和机理还欠缺很多[6],所以当进行冲击载荷作用下的机械零部件疲劳寿命计算时,只能是近似程度的,综合考虑多次冲击载荷作用的特性,依据实际机械零部件的工况确定疲劳损伤破坏类型,按照相关的疲劳损伤理论对冲击载荷作用下疲劳损伤的强度和寿命问题进行求解[7]。
为找出更合适本次密封杆寿命分析的方法,本研究将以550 kV断路器密封杆为研究对象,通过实验获得载荷情况并利用柔性体运动仿真分析,得到密封杆在运动过程中的受力情况,完成疲劳寿命预测,并与实验结果进行对比分析。
1 ADAMS与ANSYS联合仿真
一方面ANSYS进行模态分析时可生成ADAMS使用的模态中性文件,该文件将零部件当作柔性体输入到ADAMS中,利用模态叠加法计算其在动力学仿真过程中的变形及连接点上的受力情况。即考虑了零部件的弹性特性,提高仿真精度。另一方面ADAMS可将分析结果生成ANSYS可使用的载荷文件,便于ANSYS后续进行疲劳分析等[8-9]。
1.1 柔性模型建立及网格划分
此次分析以550 kV GIS断路器的密封杆为研究对象,杆的直径为φ31.5 mm,两孔之间距离为605 mm,材料为铬镍合金钢30CrNi3,抗拉强度为980 MPa,屈服强度为785 MPa。笔者利用Solidwork建立三维模型,将模型导入ANSYS,设置弹性模量、泊松比、密度等参数;本体利用Solid45单元进行网格划分,刚性连接点利用MASS21单元进行网格划分。
1.2 载荷的测量
目前,对于断路器气流场的仿真分析还不成熟,为了得到密封杆较为准确的受载荷情况,笔者分别组织实验测量了应力时间曲线和合分闸行程时间曲线,试验工况如图1所示。

图1 应力测量位置1—应力测量应变片贴片位置;2—行程测量滑线变阻器安装位置
实验数据的采集如下:应变片将应变传至应变计DB 120T-8,然后又将应变值传入应变输入模块Strain NDIS,最终由DL750示波器显示,将示波器与装有Xviewer软件的电脑相连接保存采集数据。
本次测量采集频率设为200 kHz,由于分闸时间为20 ms左右,分闸继电器响应时间小于20 ms;采集时间设为100 ms;采集进行了多次。
其中一次的分闸结果如图2所示。

图2 采集所得的数据
1.3 柔性仿真
1.3.1 模型建立
本研究利用ADAMS对密封杆进行运动分析,由于550 kV断路器运动为直线运动,可将运动部件简化为一个质量块。
运动模型简化如图3所示。

图3 运动模型简化
应力测试结果施加于左连杆的节点上,同时设置连接杆的质量为0.001 kg,故其对运动的影响可忽略不计;中间密封杆为要研究对象由上述ANSYS生成;行程曲线施加于右连杆与地面形成的滑动副上,右连杆为简化质量块。
1.3.2 输入载荷及应力应变分析
上文所述由实验采集得到的数据为电压信号,行程曲线测量通过电压—位移转化,力测量通过电压—应变—应力—拉力值转化,并在Matlab中进行拟合,得到仿真所需的曲线。该计算模型左、右连杆与地面均设置为移动副,与密封杆均设置为铰链连接,因此该模型自由度计算如下式所示:
F=3×3-2×4=1
(1)
当将行程曲线施加于右连杆与地面的移动副上之后,该模型的运动规律已经确定,软件将进行运动分析,这样就可以保证密封杆的运动为实际运动,受力也符合实际情况,同时将该构件设置为柔体,考虑其弹性;因此其计算更加准确。本研究通过运动仿真计算得到密封杆的载荷文件(.lod),该文件包含了柔性体在运动过程中不同时刻点的运动状态和所承受的载荷信息,包括力、力矩、加速度、角速度及角加速度。本研究将该载荷文件导入ANSYS中进行受力分析。
2 ADAMS与ANSYS联合仿真
由于该密封杆的疲劳型式未定,本次研究利用N_code designlife对该密封杆分别进行了名义应力法寿命分析及局部应力应变法寿命分析;并将两者的分析结果进行对比分析。
疲劳分析的流程如图4所示[10]。
2.1 名义应力法分析
名义应力法是以S-N寿命曲线为基准[11],考虑疲劳极限修正系数、切口影响系数、尺寸影响系数、加工效果影响系数及载荷计算修正系数,将总体影响系数设置为0.8。
计算结果如图5所示。
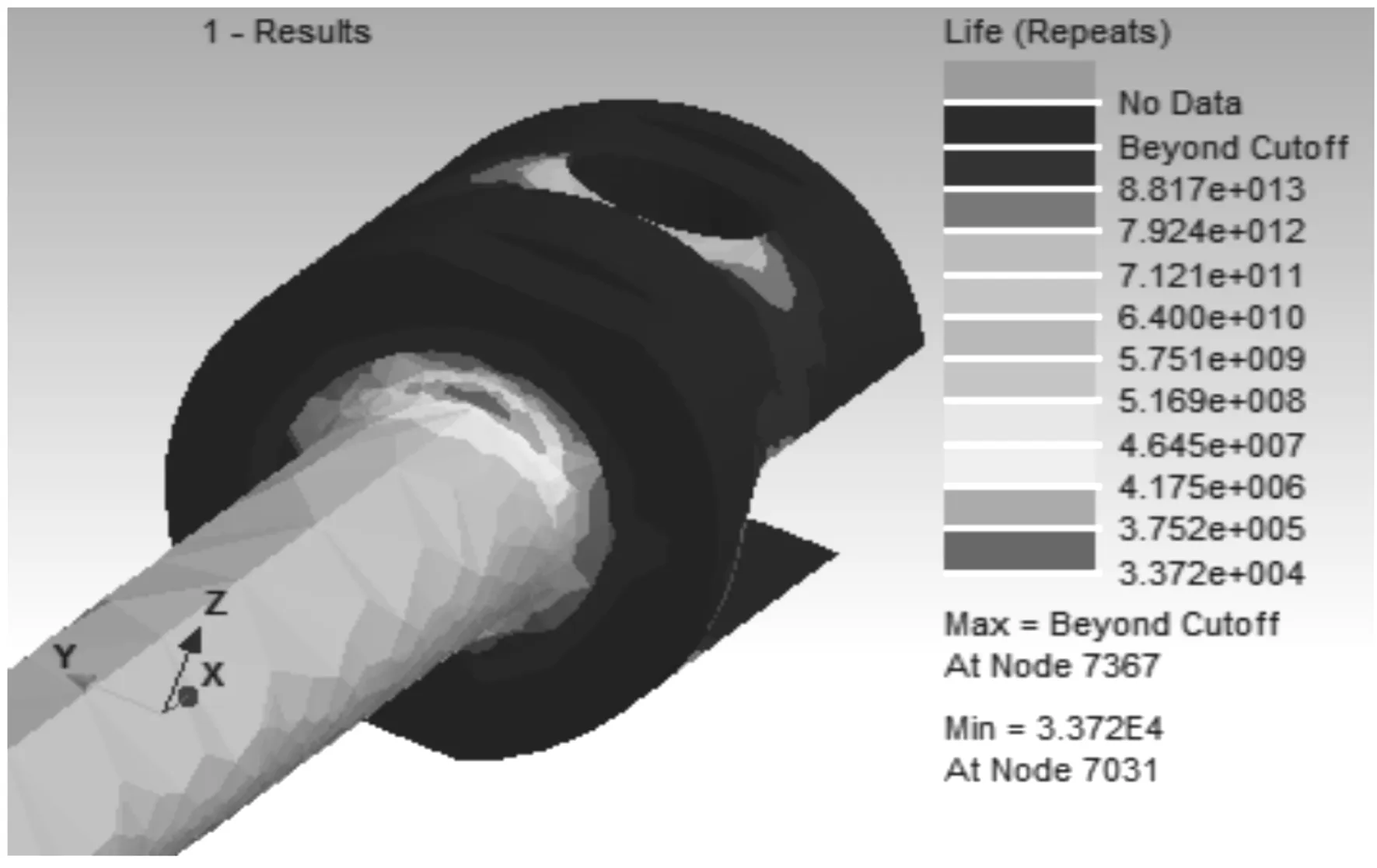
图5 S-N分析结果
2.2 局部应力应变法寿命分析
局部应力应变法是以ε-N寿命曲线为基准,设置同上。
计算结果如图6所示。

图6 ε-N分析结果
计算显示:利用名义应力法分析,该密封杆的最小寿命为33 720次。利用应力应变法分析,该密封杆的最小寿命为80 040次。由于名义应力法是以 材料的S-N曲线为基础进行寿命计算,适用于高周疲劳设计(104~105以上),局部应力应变法是以ε-N曲线为基础进行寿命计算,适用于低周疲劳设计(104~105以下),导致该杆件仅通过设计寿命次数(10 000)无法选择疲劳分析理论;而不同的疲劳分析理论又会导致不同的计算结果;学者王显会、石磊等[12]提出零部件在运动过程中所受最大应力小于材料80%的屈服强度时,利用名义应力法分析结果更为合理。
考虑到该零部件最大应力为391.8 MPa,小于628 MPa(0.8×785),本文认为该杆件的理论计算寿命取名义应力法分析结果33 720次。
3 实验结果
按国标GB-1984要求,该杆随样机进行了万次寿命型式试验(操作10 000次),顺利通过;为得到操作杆的真实寿命,在后续操作至23 300次时发生断裂。
该实验结果表明:使用名义应力法对该杆的疲劳寿命进行预测,更接近实际,可以给该杆的设计提供较合理的依据。
同时,该结果为万次寿命实验中其他运动零部件的寿命预测提供了一种方法。
4 结束语
在高压电器行业,万次寿命实验是考核产品机械性能最主要实验,决定着产品质量的优劣与运行的可靠性。目前,行业内对运动部件疲劳寿命的研究尚少,很少考虑弹性对运动件寿命的影响;本研究以550 kV断路器用密封杆为分析对象,提出了仿真分析思路,并将分析结果与实验进行对比。研究结论如下:
(1)利用应变片、示波器、Xviewer等软硬件进行应力测量,可以时时记录采样频率对应每个时刻点的应力值,为后续的分析计算提供了丰富可靠的数据支持;
(2)利用ADAMS与ANSYS联合仿真的方法,很好地结合了两者的优点,充分考虑了弹性运动部件受力及变形的影响;
(3)在万次寿命实验中,该结论可为未知疲劳型式的零部件的寿命预测提供了一种方法,可分别按照S-N及ε-N曲线进行寿命分析,并通过最大应力值与材料80%屈服强度的大小对比,得出疲劳寿命。
[1] 王建华.高压断路器——理论、设计与试验方法[M].北京:机械工业出版社,2015.
[2] 赵少汴,王忠保.疲劳设计[M].北京:机械工业出版社,1992.
[3] N E弗罗斯特.金属疲劳[M].北京:冶金工业出版社,1984.
[4] 王明珠.结构振动疲劳寿命分析方法研究[D].南京:南京航空航天大学航空宇航学院,2009.
[5] 王 莹,赵 杰,刘 录,等.基于一体化模型的往复式压缩机管线系统振动分析[J].流体机械,2015(11):22-28,42.
[6] WIRSCHING P H, SHEHATA A M. Fatigue under wide band random stress[J].JournaloftheStructuralDivision,1980,99(3):1593-1606.
[7] 李 昆.冲击载荷下机械零部件疲劳分析方法及其应用研究[D].合肥:合肥工业大学机械工程学院,2012.
[8] 李增刚.ADAMS入门详解与实例[M].北京:国防工业出版社,2013.
[9] 王树伟.ANSYS14完全自学一本通[M].北京:电子工业出版社,2013.
[10] 闻邦椿.机械设计手册(第六册)[M].5版.北京:机械工业出版社,2010.
[11] BUCH A. Fatigue strength calculation[M]. Brookfield: Trans Tech Pub.,1988
[12] 王显会,石 磊.某特种车架在冲击载荷下的瞬态响应分析及疲劳寿命评估研究[J].汽车工程,2009,31(8):769-773.

