煤层底板突水危险性评价的RS-GSVM模型
路亚彬 马良俊,2
(1.北京中安科创科技发展有限公司;2.中国安全生产科学研究院)
随着矿井开采深度和强度不断加大,煤层底板突水问题日益严重,因突水灾害造成的矿井人员伤亡和经济损失一直居高不下[1]。因此,如何快速、准确地预测矿井突水,对于保障矿山安全生产意义重大。经典的矿井突水预测方法和理论有突水系数法[2]、“下三带”理论[3]、脆弱性指数法[4]等,该类方法和理论对于有效开展矿井突水灾害防治工作发挥了积极作用。近年来,随着各领域研究工作的交叉性、耦合性愈发凸显,一些学者将模糊数学[5]、聚类分析[6]、证据理论[7]等方法创新性地应用于矿井突水预测领域,大大丰富了该领域的理论研究成果,为高效开展井下涌水防治工作拓宽了思路。但由于矿井深部的水文地质条件非常复杂,不同条件的矿井甚至同一矿井中不同位置的突水影响因素也有差异,使得突水发生存在很大的瞬时性、不确定性和难预测性,此外,在实际突水预测工作中获取大量的突水样本数据也一直是一个难点。采用上述方法对矿井突水进行分析预测时,一般选择的突水影响指标之间不可避免的存在非线性和耦合性,从而增加了井下突水预测难度。上述方法难以实现在有限的样本数据前提下对样本数据冗余属性进行约简以减少其耦合性,以及在有限样本数据上进行有效的信息深度挖掘和学习。
近年来,机器学习、人工智能、大数据分析和深度挖掘技术发展迅猛,并在各领域的应用日趋广泛。总体上,该类技术的显著优势在于可通过挖掘历史数据内在的知识和规则来对具有类似条件的工程问题进行合理判断[8]。支持向量机(SVM)[9]是一种建立在统计学VC维理论和结构风险最小原理基础上的新型机器学习算法,能够有效解决矿井突水样本数量少、非线性等实际问题。李颖[10]将SVM较早地应用于预测煤层底板突水;姜谙男等[11]将最小二乘支持向量机用于煤层底板突水量预测;曹庆奎等[12]将模糊理论和SVM相结合应用于底板突水危险性评价;闫志刚[13]将改进的SVM模型应用于识别矿井涌水水源。上述研究成效显著,不足在于未能较全面地考虑原始数据存在噪声及冗余信息的特点,在一定程度上影响了模型预测精度。粗糙集(RS)[14]无需预先给定某些特征或属性的数量描述,可在保持分类能力不变的前提下从粗糙信息中寻找规律并进行知识约简。为此,本研究充分顾及了RS冗余属性约简功能以及SVM智能学习的特点,将两者进行有机结合,并应用于对煤层底板突水危险性进行评价。针对SVM人为确定关键参数的局限性,引入了具有全局搜索功能的遗传算法(GA)[15]对SVM的关键参数进行寻优,构建基于RS-GSVM的突水危险性评价模型。
1 模型原理
1.1 RS
RS是由波兰学者Z.Pawlak于1982年提出,其主要研究对象为由四元组组成的知识表达系统S,即
S=(U,A,V,f) ,
(1)
式中,U称为论域;A=C∩D为属性的有限非空集合,且C∩D=φ,C为条件属性集(对应突水影响因素),D为决策属性集(对应是否发生突水);V={Va|a∈A}为属性值的集合,Va为属性a的值域;映射函数f:U×A→Va为一个信息函数,用于指定对象的属性值。
具有C和D的知识表达系统称为决策表,C对D的支持度可表示为
γ(C,D)=POSC(D)/|U| ,
(2)
式中,POSC(D)为D关于C的正域,指U中所有可根据C的知识确切划入U|D类的元素集合;γ(C,D)表示在C下能够保证U|D决策类的对象比率,表示C对D的支持程度[14]。
1.2 SVM
突水问题可视为典型的二分类问题,即有突与不突2种情况[10]。SVM二分类技术的核心思想是首先将突水样本空间映射至高维特征空间,然后找出支持向量及其系数构造最优分类面。若样本集T={(xi,yi)|i=1,… ,l}(xi为输入空间参数,yi为分类标识参数,xi∈Rn,yi∈(-1,+1))线性可分,当距离超平面最近的向量与其之间的距离最大时,则称该向量集被最优超平面分开。
最优超平面求解可转换为在约束条件下求解一个二次优化问题,求得一个最优决策函数,则最优分类超平面可表示为
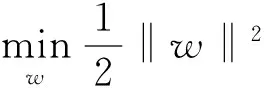
s.t.yi(w·xi+b)≥1i=1,…,l,
(3)
式中,w、b为计算系数。
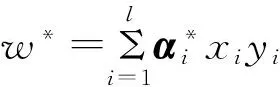
当T线性不可分时,可引入松弛变量ξ和惩罚参数C来构造最优分类超平面

(4)
求解式(4)时可引用非线性映射Φ:Rd→H,在H中构造最优分类超平面。采用满足Mercer条件的核函数K(xi,yi)=Φ(xi)·Φ(yi)代替点积运算,即:
从而得到的最终分类函数为
(6)
1.3 GA参数寻优
GA通过模拟生物进化过程,借助选择、交叉、变异等操作,经过不断迭代计算和演化得到最优解,具有较强的全局最优解搜索能力[15]。本研究利用GA对SVM参数进行寻优,流程如图1所示。
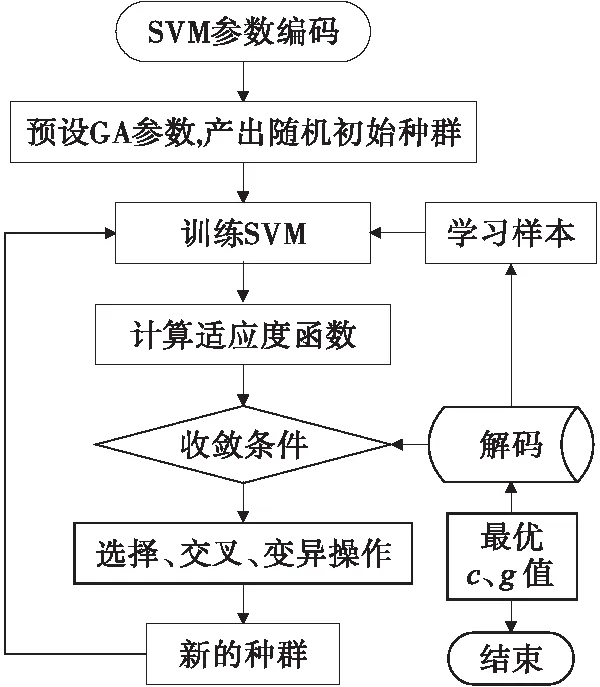
图1 SVM参数GA优化流程
常用的SVM核函数有多项式核函数、径向基函数(RBF)和Sigmoid核函数3种。RBF相对于其他函数而言,参数较少,易于寻优,故本研究选用RBF,其表达式为
K(xi,xj)=exp{-‖xi-xj‖2/2σ2} ,
(7)
式中,‖xi-xj‖为任意两点xi和xj的欧式距离;σ为RBF的扩展常数。
总体上,本研究RS-GSVM模型需要确定的参数为惩罚参数c和核参数g,两者取值在很大程度上决定了SVM的分类性能[16]。
2 煤层底板突水RS-GSVM模型评价
2.1 属性指标选取
矿井开采深部水文地质条件非常复杂,突水灾害发生受到了多种因素的影响。突水危险性评价前提是选择影响突水发生的属性指标,属性指标选取过多会增加模型的复杂程度与评价难度,甚至会掩盖影响突水发生的关键因素,指标过少又难以全面反映突水危险性状态,易降低评价结果的可靠性[17]。本研究在详细分析前人研究成果[1-7,10-13,18-20]的基础上,综合考虑了突水影响属性指标所应具有的可取性、代表性和简练性特征,选取含水层水压(X1)、采高(X2)、隔水层厚度(X3)、断层落差(X4)、煤层倾角(X5)和断层距工作面距离(X6)等作为突水危险性评价的原始属性指标。
2.2 样本数据选取
数据挖掘和分析的前提是有实际意义的样本数据。本研究选用文献[19]提供的数据,其中训练样本集20组,测试样本集5组,分别如表1、表2所示。其中,训练样本集中论域为U={a1、a2,…,a20},影响突水的属性指标作为条件属性C={X1、X2、X3、X4、X5、X6},突水危险性情况作为决策属性D={是、否}(“是”代表突水,“否”代表不突水)。RS理论要求分析数据须以类别的形式出现,而实际突水数据均为连续属性,故须对其进行离散化处理。本研究采用无监督离散算法中的等频离散算法进行处理,结果如表3所示(其中“1”代表突水,“2”代表不突水)。

表1 原始样本数据
2.3 RS属性约简
属性约简与核是RS的2个重要概念,核属性是指所有必不可少的属性集合,属性约简即删除决策表中不相关或不重要的属性,并且能保证正确分类的最小属性集C[14]。RS理论中关于属性的约简已证明是一个NP问题,一个决策表可能会有多个约简,而大多数应用中无需找到所有的约简。本研究采用了文献[20]提供的粗糙集决策表约简程序进行依赖度分析、求核和属性约简。具体步骤为:

表2 测试样本数据

表3 原始决策表
(1)依赖度分析。加载决策表数据至程序中,调用函数POS(C,D,X),计算C与D之间的依赖程度γ(C,D),γ(C,D)∈[0,1]。若输出比率为1,则说明决策属性集合D完全依赖于条件属性集合C。
(2)核属性。调用函数core(C,D),运行结果如图2所示,得到X1和X32个核心属性,即含水层水压和隔水层厚度。
(3)属性约简。调用函数redu(C,D,X),得出的约简结果与POS(C,D,X)函数运行结果相同。分析可知:X1与X32个影响因素在突水过程中起到了非常关键的作用,但结合本研究有关属性指标选取的讨论,并参考文献[14],可知在有效降低样本维数的同时保留一定的冗余属性有助于提高训练模型的抗信息丢失能力和泛化性。综合考虑各方面因素,本研究选择属性X1、X3、X5、X6作为条件属性,并通过检验验证了该选择的科学性。
(4)删除决策表中冗余属性X2和X4,并进一步删除决策表中的重复对象a8和a11。

图2 RS程序求核运行结果
2.4 SVM参数优化
2.4.1 样本归一化
为消除训练学习样本不同量纲和变化范围带来的影响,需对RS处理后的训练集原始数据进行归一化处理。处理方法可描述为
x*=(x-xmin)/(xmax-xmin) ,
(8)
式中,xmin为样本数据最小值,xmax为样本数据最大值。
2.4.2 参数设置
本研究GA关键参数设置如表4所示。

表4 GA参数设置
2.4.3 模型构建
本研究根据多代进化获得的优化的SVM参数构建了RS-GSVM评价模型。
2.4.4 模型检验
采RS-GSVM模型对测试集进行预测,若预测精度不符合要求,则需重新设置GA参数并进行模型训练。在预测精度符合要求的前提下,构建最佳参数组合的SVM模型,并进一步对其泛化能力进行检验。本研究模型利用了gatbx遗传工具箱和Libsvm-3.1工具箱,相关程序在MATLAB软件平台上进行编程实现。经过100代进化后,得到的最佳参数c=20.078 8,g=0.363 16。
2.5 煤层底板突水危险性评价
分别采用RS-GSVM模型、GSVM模型以及文献[19]、文献[20]提出的模型对表2典型工作面进行突水危险性评价,结果见表5。
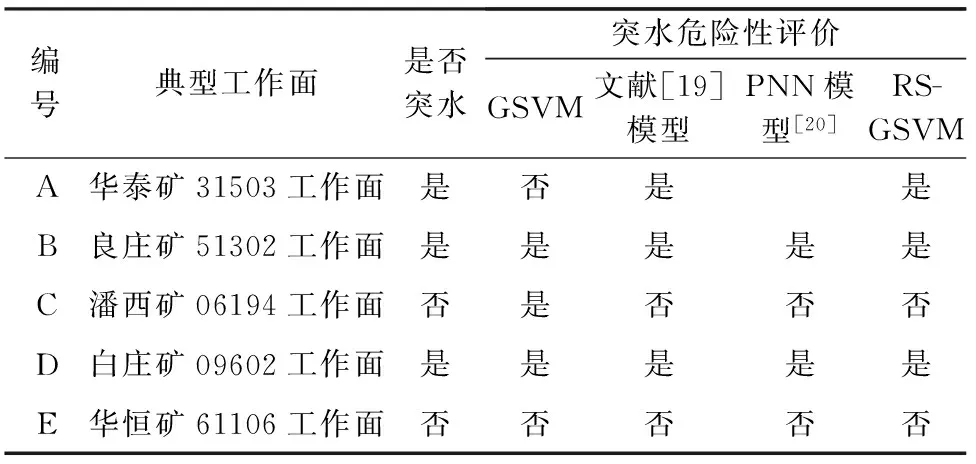
表5 煤层底板突水危险性评价对比
由表5可知:RS-GSVM模型的评价结果与5个典型工作面的煤层底板突水情况一致,其评价精度总体优于PNN模型[20]以及GSVM模型,可见本研究通过RS对冗余属性进行适当约简有助于提高模型的评价精度。
为进一步验证RS-GSVM模型的泛化能力,根据本研究确定的影响属性指标,查找相关文献[10-20]收集了7组样本数据,构建了新的预测样本集C″,对该模型进行了检验,结果如表6所示。分析表6可知,RS-GSVM模型的评价精度达到85.7%,在实际井下生产工作中,可对突水危险性进行准确评价和预测。
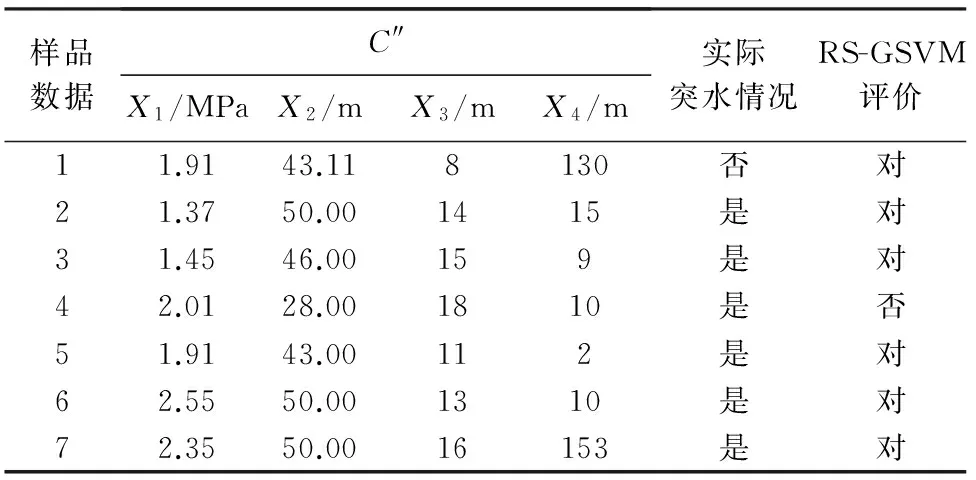
表6 RS-GSVM模型泛化能力测试
3 结 语
将RS理论与SVM模型相结合,采用遗传算法对SMV模型进行了参数寻优,构建了一种煤层底板突水危险性评价的RS-GSVM模型。该模型运用RS理论属性约简功能对煤层底板突水原始样本数据进行预处理,删除了原始样本数据中冗余属性和重复样本,降低了样本空间维数,既精简了样本数量,又提高了模型的训练速度和评价精度。试验表明:RS-GSVM模型对于煤层底板突水危险性的评价精度优于GSVM模型以及PNN模型,对于高精度评价和预测煤矿井下突水灾害有一定的借鉴价值。
[1] 王朋飞,李翠平,李仲学,等.基于层次分析法的矿井突水风险评价[J].金属矿山,2012(12):95-98.
[2] 乔 伟,李文平,赵成喜.煤矿底板突水评价突水系数-单位涌水量法[J].岩石力学与工程学报,2009(12):2466-2474.
[3] 李白英.预防矿井底板突水的“下三带”理论及其发展与应用[J].山东科技大学学报(自然科学版),1999(4):11-18.
[4] 武 强,张志龙,张生元.煤层底板突水评价的新型实用方法II:脆弱性指数法[J].煤炭学报,2007,32(11):1121-1126.
[5] 刘伟韬,张文泉,李加祥.用层次分析-模糊评判进行底板突水安全性评价[J].煤炭学报,2000(3):278-282.
[6] 王静宇,李翠平,李仲学.基于主成分聚类分析的煤层底板突水危险性预测[J].中国安全科学学报,2013(8):120-125.
[7] 肖建于,童敏明,姜春露.基于模糊证据理论的煤层底板突水量预测[J].煤炭学报,2012(S):131-137.
[8] 姜安龙,戚玉亮.粗糙集-BP神经网络组合方法及其应用[J].中南大学学报(自然科学版),2011(10):3189-3194.
[9] VAPNIK W N.统计学习理论的本质[M].张学工,译.北京:清华大学出版社,2000.
[10] 李 颖.基于支持向量机的煤层底板突水预测方法研究[D].北京:煤炭科学研究总院,2007.
[11] 姜谙男,梁 冰.基于最小二乘支持向量机的煤层底板突水量预测[J].煤炭学报,2005(5):71-75.
[12] 曹庆奎,赵 斐.基于模糊-支持向量机的煤层底板突水危险性评价[J].煤炭学报,2011(4):633-637.
[13] 闫志刚.SVM及其在矿井突水信息处理中的应用研究[J].岩石力学与工程学报,2008(1):215-216.
[14] PAWLAK Z.Rough Sets-theoretical Aspects of Reasoning about Data[M].Dordrecht:Kluwer Academic Publishers,1991.
[15] HOLLAND J H.Adaptation in Natural and Artificial Systems[M].Ann Arbor:University of Michigan Press,1975.
[16] 李良敏,温广瑞,王生昌.基于遗传算法的回归型支持向量机参数选择法[J].计算机工程与应用,2008(7):23-26.
[17] 张文泉,张广鹏,李 伟.煤层底板突水危险性的Fisher判别分析模型[J].煤炭学报,2013(10):1831-1836.
[18] 武 强,张志龙,马积福.煤层底板突水评价的新型实用方法Ⅰ:主控指标体系的建设[J].煤炭学报,2007(1):42-47.
[19] 施龙青,谭希鹏,王 娟,等.基于PCA_Fuzzy_PSO_SVC的底板突水危险性评价[J].煤炭学报,2015(1):167-171.
[20] 邵良杉,徐 波.煤层底板突水危险性的PNN预测模型研究及应用[J].中国安全科学学报,2015(8):93-98.

