新型自复位钢桁架梁的受力机理及抗震性能

杨溥,高浩捷,蔡森,黄诚

(1.重庆大学 a.山地城镇建设与新技术教育部重点实验室; b.土木工程学院 重庆 400045；2.中机中联工程有限公司 重庆 400039)

传统的钢框架结构主要通过梁、柱等结构构件的塑性变形来耗散地震能量，震后结构将产生较大的塑性残余变形，导致结构难以修复甚至只能拆除重建，从而造成巨大的经济损失。自复位结构是一种旨在减少或消除结构“残余变形”的新型结构形式，为解决上述问题提供了一种有效的办法。近些年，学者们对自复位构件或结构的研究也日益增多。

自复位钢框架结构最早由Ricles等[1-2]提出，基本组成构件包括柱、钢框架梁、预应力钢绞线以及角钢等部件。Garlock等[3-7]通过理论研究与试验证明了自复位钢框架拥有良好的抗震性能，而且结构的残余变形很小。Ricles等[8]和Lin等[9]使用摩擦型阻尼器来代替角钢，设计了一栋设置了该装置的缩尺结构，试验结果表明其残余层间位移角小于0.075%，有较好的结构抗震可恢复能力。Angelos等[10]在自复位梁柱节点的梁端腹板设置了沙漏状的粘滞阻尼器，并对比分析了在不同地震水准输入下该类结构的响应规律，结果表明，即使在最大地震作用下梁和柱脚均未出现塑性铰，说明此类粘滞阻尼器能有效提高结构抗倒塌能力以及减小结构残余变形。

潘振华等[11]对9个自复位钢框架足尺边节点进行了模拟，证明了该类节点具有很好的弹性刚度、延性和强度，且能达到预期的耗能性能与自复位能力目标。宋良龙等[12]、郭彤等[13]、Song等[14]通过数值模拟分析了腹板摩擦式自复位钢筋混凝土框架梁柱节点中钢绞线预应力对节点刚度、残余变形以及耗能的影响规律。并在此基础上进行了采用该梁柱节点的单层单跨结构缩尺试验，结果表明：2.5%的层间位移下混凝土梁只有少量损伤，而混凝土柱则无损伤。蔡小宁等[15-16]提出一种自复位钢筋混凝土预制节点，对该节点进行低周往复试验，并基于OpenSees提出了该节点的数值模拟方法，研究结果表明：该数值模拟方法结果与试验结果吻合较好，精度可满足工程需求。张艳霞等[17]、张爱林等[18-19]提出了一种腹板摩擦耗能的自复位钢框架体系，该体系能够实现在施工现场地面张拉预应力钢绞线，梁柱节点只需像传统梁柱节点一样采用栓焊混合的方法进行连接；设计了一栋4层原型结构，进行了0.75倍缩尺的子结构拟动力加载试验，并对其进行了数值分析及动力时程分析。

目前，关于自复位梁柱节点的研究虽然取得了不少成果，但由于自复位梁与柱之间在水平荷载作用下会产生缝隙，从而要求与梁相连的楼板需进行特殊设计，在一定程度上限制了其应用。自复位钢桁架梁由于直接铰接于框架柱，且通过特殊加工使桁架梁下弦杆可以和桁架之间能有相对位移。在水平荷载下桁架与下弦杆之间出现缝隙，而梁柱之间不会出现缝隙，地震过程中柱间距保持不变，从而较好地解决了这一问题。通过理论推导和非线性模拟分析，研究自复位钢桁架梁的受力机理，考察其自复位能力、耗能以及破坏模式等抗震性能。

1 自复位钢桁架梁的受力机理及力学特性

1.1 自复位钢桁架梁的受力机理

自复位钢桁架梁的构造如图1(a)所示。其中，桁架梁上弦杆铰接于框架柱，下弦杆采用内外套管(见图1(b))。下弦内管两端与柱铰接，在外套管两端设置只能向两端方向移动的锚固板，在两个锚固板之间设置预应力筋，将内外套管预压在一起，作为自复位梁的“下弦杆”，在框架柱与外套管端部之间设置防屈曲消能杆，防屈曲消能杆由耗能钢筋和外包防屈曲圆钢套管组成。防屈曲消能杆通过连接器和构件相连，这样可以方便地更换消能杆。当该框架受到向右的水平荷载时，其变形如图1所示，上弦杆及腹杆带动下弦外管向右移动，压迫右侧锚固板右移，而左侧锚固板受内管限制不能向右移动，于是产生缝隙(图1(a)中Δgap)，消能杆开始变形耗能，而预应力钢绞线的预应力使锚固板回位，从而为桁架梁提供复位性能。

图1 自复位钢桁架的构造图Fig.1 Drawing of self-centering steel truss beam configuratio

1.2 自复位钢桁架梁的力学特性

图2 钢绞线和消能杆的轴力变形曲线Fig.2 Axial force-deformation curve of fuse and PT stran

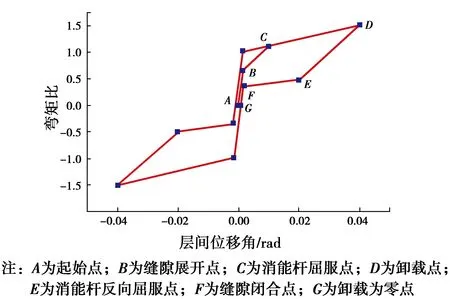
图3 自复位钢桁架的弯矩比层间位移角曲线Fig.3 Moment ratio-interstory drift curve of the bea

1)第1阶段：该阶段所有组件处于弹性状态(图3中A-B段)，外套管和内锚固板之间没有出现缝隙，内外套管作为一个整体共同受力，钢绞线应力保持不变，受力特征和弹性状态下的普通钢桁架梁相似。

2)第2阶段：该阶段已出现缝隙但消能杆尚未屈服(图3中B-C段)，加载到B点时，外套管和内锚固板之间出现缝隙，钢绞线随之伸长而应力增大，该阶段构件的抗侧移刚度主要由消能杆提供，所以刚度有所降低，到C点时消能杆屈服。

3)第3阶段：此阶段内消能杆已经进入屈服状态(图3中C-D段)，加载到C点时，消能杆屈服。此时消能杆不提供刚度，构件抗侧移刚度即为钢绞线刚度，刚度再次降低。

4)第4阶段：该阶段为卸载段，消能杆尚未反向屈服(图3中D-E段)，加载到D点时，正向加载到达最大值，消能杆处于屈服状态。此阶段内消能杆由正向屈服开始卸载，并在钢绞线复位力作用下最后反向屈服，该阶段卸载刚度主要由消能杆提供，其刚度和B-C段相同。

5)第5阶段：此卸载段消能杆已经反向屈服，但缝隙尚未完全闭合(图3中E-F段)，卸载至E点，消能杆反向屈服。此时消能杆不提供刚度，其卸载刚度即为钢绞线刚度，其刚度和C-D段相同。

6)第6阶段：该阶段内外套管和锚固板之间的缝隙已经完全闭合(图3中F-G段)，卸载到F点时缝隙正好闭合。内外套管重新作为一个整体共同受力，其卸载刚度增大，最终直至卸载完成的G点。

2 自复位钢桁架梁的理论分析

2.1预应力钢绞线与消能杆对梁抗弯能力的贡献分析

假设钢绞线的面积为Apt，长度为Lpt，弹性模量为Ept，则钢绞线的轴向拉伸刚度Kaxial为

(1)

钢桁架梁出现缝隙后，钢绞线相应沿轴向产生变形，钢绞线变形提供的抵抗弯矩M1为

(2)

式中:htruss为桁架梁的梁高，梁高为下弦杆件横截面中心线至上弦杆件横截面中心线的长度(见图1b)，δ1为预应力钢绞线的伸长值。

由于外套管通过腹杆与上弦杆连接，在水平荷载作用下，外管与内管产生位移差，该值与预应力钢绞线的伸长值相等。于是，桁架梁截面产生的转角φ1为

(3)

桁架梁抗弯刚度中由预应力钢绞线提供的抗弯刚度Kpt为

(4)

同理，假设消能杆面积为Afu，弹性模量为Efu，长度为Lfu，则消能杆的轴向刚度Kfuse为

(5)

由消能杆在钢桁架梁内部产生的抵抗弯矩M2为

(6)

式中：δ2为消能杆的轴向变形。

消能杆产生轴向变形δ2后，桁架梁截面产生的转角φ2为

(7)

因此，消能杆对钢桁架梁提供的抗弯刚度Kf为

(8)

2.2 自复位钢桁架梁的受力特性分析

为了确保自复位钢桁架梁的可更换性与自复位能力，在地震过程中，桁架梁的上、下弦件和腹杆均应保持弹性。因此，根据梁的受力状态确定其恢复力骨架曲线关键特征点处的梁端弯矩及刚度值，以供结构初步设计时参考。

1)第1阶段(尚未出现缝隙)，该阶段内外套管和内锚固板间没有出现缝隙，钢绞线没有出现变形，其应力也基本不变，受力特征和弹性状态下的普通桁架梁相似，该阶段桁架的抗弯刚度K1为

K1=Ktruss

(9)

式中：Ktruss为桁架的弹性抗弯刚度。

设f0pt为预应力钢绞线的初始应力。当刚好出现缝隙时，内外套管间的轴力差值为

F=Aptf0pt

(10)

此时钢桁架梁所能承受的最大弯矩Mgap为

Mgap=Aptf0pthtruss

(11)

2)第2阶段(已经出现缝隙，消能杆尚未屈服)，该阶段桁架的抗侧移刚度主要为预应力筋与消能杆并联提供，刚度K2为

(12)

由于该阶段预应力筋提供的刚度远小于消能杆提供的刚度，所以,在此阶段所增加的弯矩全部由消能杆承担，消能杆屈服时能承受的最大弯矩Mfuse为

Mfuse=Kfuseδyhtruss

(13)

式中：δy为消能杆屈服时的轴向变形。

因此，消能杆屈服时钢桁架梁所能承受的最大弯矩My为

My=Mgap+Mfuse=Aptf0pthtruss+Kfuseδyhtruss

(14)

3)第3阶段(消能杆已经屈服，钢绞线尚未屈服)，该阶段钢桁架梁的抗侧移刚度主要由预应力筋提供，此阶段的刚度K3为

(15)

钢绞线屈服时，消能杆承担的弯矩基本不变，钢绞线承担的弯矩Mypt为

Mypt=Aptfypthtruss

(16)

式中：fypt为预应力钢绞线的屈服应力。

因此，钢绞线屈服时钢桁架梁所能承受的最大弯矩Mu为

Mu=Mypt+Mfuse=Aptfypthtruss+Kfuseδyhtruss

(17)

在实际情况中，更换预应力钢绞线比较困难，同时,为了保证自复位桁架梁的耗能和复位能力，通常不允许预应力钢绞线屈服，式(17)仅为了给出钢桁架梁的极限弯矩。对于本文的构件，即使预应力钢绞线屈服，桁架梁仍具有较高的承载能力，但其复位能力将明显下降。

3 自复位钢桁架梁的抗震性能模拟分析

3.1 算例概况

算例采用如图4所示的自复位钢桁架梁，楼层层高为3 m，桁架梁高为600 mm，桁架梁跨度为6 m。框架柱、上下弦杆和腹杆等杆件均采用Q345钢材，桁架梁的主要结构参数见表1。

图4 自复位钢桁架梁算例示意图Fig.4 Analytical model of self-centering steel truss bea

构件类型截面类型截面尺寸弹性模量/MPa屈服强度标准值/MPa框架柱H型500mm×500mm×20mm×20mm2.06×105325上弦杆方管160mm×160mm×10mm2.06×105345腹杆方管120mm×120mm×5mm2.06×105345内套管方管200mm×200mm×10mm2.06×105345外套管方管250mm×250mm×6.5mm2.06×105345

为了考察预应力筋和防屈曲消能杆参数对自复位钢桁架梁耗能和复位性能的影响，引入一个SC参数，其定义为预应力筋的初始应力对整体弯矩的贡献与防屈曲消能杆屈服时对整体弯矩的贡献之间的比值，即

(18)

研究表明，当SC参数较小(如小于1.0)时，由于预应力筋提供的恢复力相对较小，梁的残余变形较大，复位效果不理想。随着SC参数的增加，构件滞回曲线在控制残余变形的同时，相对更加饱满，SC参数值建议取1.0～1.5[21]。算例中SC为1.35。

3.2 非线性分析模型

柱脚与基础、桁架梁上弦杆和下弦内杆与柱之间均采用铰接，框架柱和梁构件均采用基于柔度的非线性梁柱单元的纤维模型进行模拟，下弦外管与锚固板、内管与锚固板之间采用只受压不受拉的零长单元(图4中单元①、②)，材料为受拉刚度为零的弹性材料，其受压模拟的是锚固板与内套管两块钢板之间的挤压，受压弹性模量取较大的数值(2.0×1010MPa)。该单元受拉时的伸长量即为缝隙宽度(图1(a)中Δgap)。

预应力钢绞线采用truss单元模拟，材料为考虑初始应力的steel01，由于预应力钢绞线没有明显的屈服极限，所以取钢绞线卸载后的残余变形达到0.2%时对应的应力f0.2为屈服应力，约1 600 MPa，其恢复力曲线见图2(b)。

在整个加载过程中，防屈曲消能杆仅沿轴向变形，并通过消能杆的塑性变形进行耗能，所以,采用truss 单元来模拟(图4中单元③)。防屈曲消能杆在往复轴向加载过程中轴向受拉和轴向受压时都应具有良好的滞回性能，这里采用理想弹塑性材料来模拟。防屈曲消能杆的最大弹性轴向变形取为1.5 mm，其轴向刚度取为1.50×105kN/m，屈服力为245 kN，其恢复力曲线见图2(a)。

3.3 加载制度

模拟分析时，单向和往复加载均采用位移控制模式，水平荷载施加于钢框架柱的柱顶(见图4水平荷载F作用点)。

单向加载时，柱顶最大位移取为240 mm(对应的桁架的位移角为0.08 rad)；往复加载时，柱顶最大位移取为120 mm(对应的桁架的位移角为0.04 rad)。加载的最大位移对应的转角超过了抗震规范规定的框架结构的弹塑性层间位移角限值1/50(即0.02 rad)[20]。考虑到抗震规范规定的多高层钢结构的弹性层间位移角限值为1/250，在往复加载时，选择位移增量为3 000/250=12 mm。

3.4 单向加载下的力学性能

图5弯矩转角曲线Fig.5 Moment-rotation curve

图6弯矩缝隙宽度曲线Fig.6 Moment-gap width

图7 弯矩钢绞线应力曲线Fig.7 Moment-stress of PT strand

图8 刚度层间位移角曲线Fig.8 The stiffness-drift rati

表2列出了数值模拟分析结果与理论公式的计算值对比，可以看出，各阶段的刚度和临界弯矩值拟合情况很好。

表2 特征点弯矩和刚度模拟值与理论值对比Table 2 Comparison of critical moment and stiffness at major points between simulation and theoretical value

注：括号内的值为理论计算值。

3.5 往复加载下的力学性能

图9 弯矩转角曲线Fig.9 Moment-rotation curve

图10 弯矩缝隙宽度曲线

图11 弯矩钢绞线应力曲线图Fig.11 Moment-stress of PT strand

图12 弯矩转角曲线图Fig.12 Moment-rotation curv

4 结论

提出了一种新型自复位钢桁架梁，通过理论推导和有限元分析，得到了以下结论：

1)理论推导了自复位钢桁架梁端对应于其恢复力曲线关键特征点(缝隙出现、消能杆屈服等)处的刚度和临界弯矩值，并与有限元模拟结果进行了对比，验证了提出的该新型自复位钢桁架梁的非线性模拟方法的有效性。

2)通过往复加载下的分析结果，证明了自复位钢桁架梁具有良好的耗能消能和自复位功能，地震能量主要由防屈曲消能杆的塑性轴向变形耗散，能够达到预期的抗震性能。

[1] RICLES J M, SAUSE R, GARLOCK M M, et al. Post-tensioned seismic-resistant connections for steel frames[J]. Journal of Structural Engineering, 2001, 127(2): 113-121.

[2] RICLES J M, SAUSE R, PENG S W, et al. Experimental evaluation of earthquake resistant post-tensioned steel connections[J]. Journal of Structural Engineering, 2002, 128(7): 850-859.

[3] CHRISTOPOULOS C, FILIATRAULT A, UANG C M, et al. Post-tensioned energy dissipating connections for moment-resisting steel frames[J]. Journal of Structural Engineering, 2002, 128(9): 1111-1120.

[4] GARLOCK M E M. Design, analysis, and experimental behavior of seismic resistant post-tensioned steel moment resisting frames[D]. Lehigh：Lehigh University， 2003.

[5] GARLOCK M M, RICLES J M, SAUSE R. Experimental studies of full-scale post-tensioned steel connections[J]. Journal of Structural Engineering, 2005, 131(3): 438-448.

[6] GARLOCK M M, SAUSE R, RICLES J M. Behavior and design of post-tensioned steel frame systems [J]. Journal of Structural Engineering, 2007, 133(3): 389-399.

[7] GARLOCK M E M, LI J. Steel self-centering moment frames with collector beam floor diaphragms[J]. Journal of Constructional Steel Research, 2008, 64(5): 526-538.

[8] RICLES J M, SAUSE R, LIN Y C, et al. Self-centering moment connections for damage-free seismic response of steel MRFs[C]//Structures Congress， 2010.

[9] LIN Y C, RICLES J M, SAUSE R, et al. Earthquake simulations on a self-centering steel moment resisting frame with web friction devices[C]//14th World Conference on Earthquake Engineering. 2008.

[10] ANGELOS S T, ATHANASIOS I D, THEODOER L K. EC8-based seismic design and assessment of self-centering post-tensioned steel frames with viscous dampers [J]. Journal of Constructional Steel Research, 2015, 105: 60-73.

[11] 潘振华, 潘鹏, 叶列平,等. 自复位钢框架节点有限元模拟及参数分析[J]. 建筑结构学报, 2011, 32(3): 35-42.

PAN Z H, PAN P, YE L P, et al. Modeling and parametric study of beam-to-column connection for self-centering steel moment frames[J]. Journal of Building Structures， 2011, 32(3): 35-42.(in Chinese)

[12] 宋良龙, 郭彤. 下翼缘摩擦式自定心钢框架梁柱节点抗震性能的数值模拟[J]. 防灾减灾工程学报， 2011, 31(6): 648-653.

SONG L L, GUO T. Numerical simulation of seismic performance for self-centering steel frame beam-column connection with bottom flange friction devices[J]. Journal of Disaster Prevention and Mitigation Engineering， 2011, 31(6): 648-653.(in Chinese)

[13] 郭彤, 宋良龙. 腹板摩擦式自定心预应力混凝土框架基于性能的抗震设计方法[J]. 建筑结构学报, 2014, 35(2): 22-28.

GUO T, SONG L L. Performance-based seismic design method of self-centering prestressed concrete frames with web friction devices[J]. Engineering Structures, 2014, 35(2): 22-28.(in Chinese)

[14] SONG L L, GUO T, GU Y, et al.Experimental study of a self-centering prestressed concrete frame subassembly[J]. Engineering Structures, 2015, 88:176-188.

[15] 蔡小宁,孟少平,孙巍巍.自复位预制框架边节点组件受力性能试验研究[J].工程力学,2014, 31(3): 160-167.

CAI X N, MENG S P, SUN W W. Experimental study on performance of components of the exterior self-centering post-tensioned precast connections[J]. Engineering Mechanics,2014, 31(3): 160-167.(in Chinese)

[16] 蔡小宁, 孟少平. 预应力自复位混凝土框架节点抗震性能数值模拟[J]. 工程力学, 2016, 33(3):143-151.

CAI X N, MENG S P. Numerical analysis for seismic behavior of self-centering post-tensioned column connections [J]. Engineering Mechanics,2016, 33(3):143-151.(in Chinese)

[17] 张艳霞, 叶吉健, 杨凡,等. 自复位钢框架结构抗震性能动力时程分析[J]. 土木工程学报, 2015，48(7): 30-40.

ZHANG Y X, YE J J, YANG F, et al. Seismic behavior time-history analysis of integral steel self-centering moment resisting frame[J]. China Civil Engineering Journal, 2015，48(7): 30-40.(in Chinese)

[18] 张爱林, 张艳霞, 赵微,等. 可恢复功能的装配式预应力钢框架拟动力试验研究[J]. 振动与冲击,2016, 35(5):207-215.

ZHANG A L, ZHANG Y X, ZHAO W, et al. Pseudo dynamic tests for a resilient prefabricated prestressed steel frame [J]. Journal of Vibration and Shock,2016, 35(5):207-215.(in Chinese)

[19] ZHANG A L, ZHANG Y X, LI R, et al. Cyclic behavior of a prefabricated self-centering beam-column connection with a bolted web friction device [J]. Engineering Structures, 2016(5):185-198.

[20] 建筑抗震设计规范:GB 50011—2010[S]. 北京: 中国建筑工业出版社, 2010.

Code for seismic design of buildings:GB 50011-2010[S]. Beijing: China Architecture & Building Press, 2010.(in Chinese)

[21] 黄诚. 一种自复位钢桁架梁非线性模拟分析[D]. 重庆：重庆大学，2015.

HUANG C. Nonlinear simulation and analysis of self-centering steel truss beam[D].Chongqing:Chongqing University, 2015.(in Chinese)