翼伞系统十五自由度动力学建模与仿真
杨海鹏 贺卫亮
翼伞系统十五自由度动力学建模与仿真
杨海鹏 贺卫亮
(北京航空航天大学,北京 100191)
动力学建模是飞行器设计的基础,翼伞作为一种新型的柔性飞行器,在动力学建模方面已经有了较多研究,但仍存在诸多不足。当前翼伞的动力学模型主要有六自由度模型与九自由度模型。六自由度模型将翼伞与载荷当做一个刚体,两体之间采用固定连接;九自由度模型在六自由度模型的基础上考虑了翼伞与载荷间的相对运动,将翼伞与载荷当做两个刚体,两体之间采用铰连接。两种动力学模型都没有体现出翼伞的柔性,与真实的翼伞存在较大差距。文章载荷-翼伞多体飞行系统为研究对象,假定伞绳和吊带分别通过铰链与翼伞和载荷相连接,考虑了伞绳和吊带具有的弹性,伞绳的相交点与伞衣具备相对运动,载荷舱与翼伞除相对转动外还考虑到其相对平移,建立了翼伞十五自由度模型。施加翼伞后缘下偏并仿真计算翼伞转弯运动情况,并与九自由度模型的计算结果进行对比。结果表明,相对于九自由度模型,翼伞十五自由度能够更加真实全面地反映了翼伞的运动情况,除了翼伞的总体运动以外,还能够反映吊带、伞绳相交点的运动。
动力学建模 仿真 十五自由度模型 翼伞系统
0 引言
翼伞具备包装方便、体积小、质量轻且飞行性能良好等优点,在农业、军事、旅游等领域拥有广阔的应用前景。翼伞技术已成为国内研究热点,翼伞的动力学分析是研究新型翼伞的基础。
目前用于一般翼伞系统多体动力学特性研究的仿真模型均将伞体和有效载荷分别看作两个独立的刚体,不同之处在于连接约束模型,主要分为三类:一是假设两体通过弹簧相连,其参数的设置依赖于实际系统和仿真经验,以文献[1-3]等为代表;二是两体通过约束方程建立关系,保证了连接点空间位置的一致性,以文献[4-6]等为代表;三是假设两体共用一个坐标系原点,相对姿态关系通过扭簧建立关系,以文献[7-9]等为代表。
翼伞作为一种柔性飞行器本身具有弹性,且弹性对于运动特性具有较大影响,例如伞绳相交点相对于伞体的运动会改变翼伞的安装角进而影响翼伞性能;在翼伞实际应用过程中可能会需要改变伞舱高度,伞舱高度的调节主要通过改变吊带长度来实现,且吊带会使翼伞与载荷之间存在相对平移。九自由度模型没有体现出翼伞的上述特性。文献[10]提出将伞绳与翼伞的连接以及吊带与载荷的连接看做铰连接的方法;文献[11]提出了考虑伞绳的弹性的方法,这两种方法考虑到了吊带的影响以及翼伞与载荷的相对平移。本文在结合上述两种建模方法的基础上,既考虑伞绳与吊带的弹性又考虑伞绳、吊带与翼伞、载荷的铰连接,推导出十五自由度模型,模型一方面考虑了伞绳具备的弹性;另一方面充分考虑了翼伞与载荷的相对平移以及吊带的影响;之后对翼伞的十五自由度动力学模型运动进行仿真。
1 动力学建模
1.1 假设
图1所示,将翼伞系统简化为翼伞与载荷两个刚体,通过弹性杆件将两个刚体进行连接。翼伞与四根弹性杆件通过铰连接相连,四根弹性形杆件通过铰连接相交于c点构成的弹性框架cp。载荷与弹性杆件cd通过铰接点d相连,并与弹性框架通过铰接点c相连。
1.2 坐标系及坐标转换
如图1所示,翼伞-载荷系统总体坐标系为(c,c,c),其原点位于铰接点c,坐标轴平行于地面坐标系(e,e,e);翼伞体坐标系为(p,p,p),其原点位于翼伞质心p,本文假设翼伞质心位于翼伞中轴线上,载荷体坐标系为(b,b,Zb),其原点位于载荷质心b。
由总体坐标系向体坐标系的转换矩阵为:

1.3 动力学模型
基于动量与动量矩原理对翼伞进行单独的受力分析,翼伞受重力、气动力以及杆件cd通过铰接点c对于翼伞伞体的作用力,由于翼伞的平均密度小,动力学方程中还需要考虑附加质量。根据动量和动量距定理,翼伞的动力学方程为:

式中 Pp、Hp为翼伞的动量和动量矩分量列阵;Gp为翼伞在翼伞坐标系下的重力分量列阵;Rcp×为铰接点Oc到翼伞质心Op矢量的叉乘矩阵;Faerop和Maerop为翼伞所受气动力和气动力矩;Ωp为翼伞的角速度在翼伞体坐标系下的分量;Fc为铰接点Oc的内力在地面坐标系下的矢量;Tp为地面坐标系向翼伞体坐标系的转换矩阵;Mc为翼伞与载荷在产生相对偏航时翼伞所受的相对偏航力矩,根据Lingrad[12]提供的计算方法得到。
载荷舱受自身重力、气动力、推力以及铰接点d的作用力的影响,但是由于载荷舱平均密度大,所以动力学方程中不考虑附加质量。则载荷舱的动力学方程为:


力c、d的数值等于弹性杆件cd所受到拉力的cd,方向与弹性杆件cd平行,弹性杆cd受到拉力cd作用后会产生的形变Δcd,相互之间的关系如下式:

式中为弹性杆件cd的弹性系数。
杆件方向以及杆件形变方向与作用力方向一致。假设杆件与作用力方向在总体坐标系(c,c,c)下的方向余弦向量为=[x;y;z],且方向余弦向量满足关系:
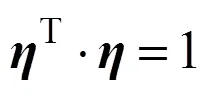
则拉伸后的杆件cd的两端在总体坐标系(c,c,c)下构成的矢量为:

式中cd为弹性杆cd受拉力时的初始长度;弹性框架cp受到杆cd的拉力后,连接点c相对于翼伞所产生的位移在翼伞体坐标系(p,p,p)下矢量为Δcp,该矢量满足如下条件:

式中为伞绳所构成的弹性框架cp的刚度矩阵。
通过式(4)、(5)、(6)、(7)可以得到:

由此得出由铰接点c到翼伞质心p的矢量cp在翼伞体坐标系(p,p,p)下表示为:
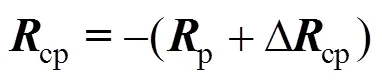
式中p为cp未受力前的初始矢量,可表示为:

式中p为未受力时点c到点p的初始长度;为伞体质心p与铰接点c的连线与p轴夹角既安装角。
另外由铰接点d到载荷质心b的矢量db在载荷体坐标系下表示为:
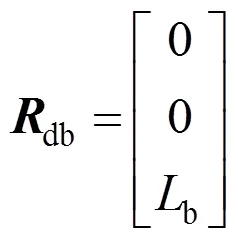
式中b为铰接点d到载荷质心b的距离。
另外翼伞与载荷在各自体坐标系下的角速度表示为:

式中p、p、p分别为翼伞的滚转、俯仰、偏航角速度;b、b、b分别为载荷的滚转、俯仰、偏航角速度。
通过分析与欧拉角速度之间的关系得到运动方程为:


根据上述各式求出翼伞十五自由度动力学方程:


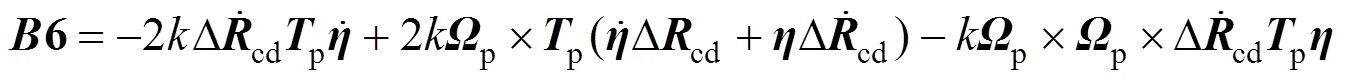
式中c为c点在地面坐标系下的速度分量。f、f分别为翼伞附加质量矩阵利用Barrows[13]提出的数值计算方法得到。p,b分别为翼伞与载荷的转动惯量。p,b分别为翼伞与载荷的质量矩阵,表示如下:

式中p为翼伞伞体质量;b为载荷质量。
1.4 翼伞参数
1.4.1 翼伞基本参数
翼伞具体设计参数如下表1所示:
表1 翼伞设计参数

Tab.1 Design parameter of parafoil
表中为翼伞弦长;为翼伞展长;为翼伞最大厚度;p为翼伞面积;b为载荷舱面积。
1.4.2 翼伞气动参数
由于本文主要研究翼伞动力学建模与分析,因此气动参数主要通过理论估算的方法获得。相关升力系数、阻力系数以及俯仰力矩系数由Lingrad提供的数据插值得到,气动力计算公式和系数计算方法来源于文献[14],其余气动数根据相关文献[15]估算得到。
2 翼伞运动仿真
2.1 九自由度模型运动对比
目前九自由度模型已经非常成熟,相关建模可直接利用参考文献[16]中已有的模型,将设计参数改为本文中翼伞采用的设计参数。对翼伞施加后缘单侧下偏控制后,会使翼伞受到非展向对称的气动力,进而实现转弯运动。假定翼伞初始水平速度为10m/s,垂直方向速度为0,初始姿态角均为0,计算翼伞在50s施加50%左侧下偏操纵后翼伞运动情况,并将计算结果与九自由度模型进行对比。目前翼伞的九自由度模型是翼伞建模中应用最为广泛的一种,大量的实验证明九自由度模型能够较为准确的反映翼伞的运动情况。图2、3、4、5为翼伞两种自由度模型翼伞与载荷的俯仰角、滚转角,翼伞与载荷的相对偏航角以及翼伞速度、攻角的对比。从图2和图3可以看出,翼伞与载荷的在受到扰动后会发生震荡,载荷的震荡频率较相对高,收敛时间相对较长,通过对比两种动力学模型的载荷的震荡情况可以明显地发现,十五自由度模型的载荷震荡幅度较大,收敛时间较长,最终稳定后两种动力学模型的翼伞与载荷的状态量基本相等。从图4中的速度可以看出飞行器最终稳定后沿总体坐标系c轴方向的速度z约为3.4m/s,沿c轴方向的速度y以及沿c轴方向的速度x呈周期性变化,由此可以得知伞翼飞行器在施加单侧下偏控制后作螺旋下降运动。

图2 翼伞运动俯仰角

图3 翼伞运动滚转角
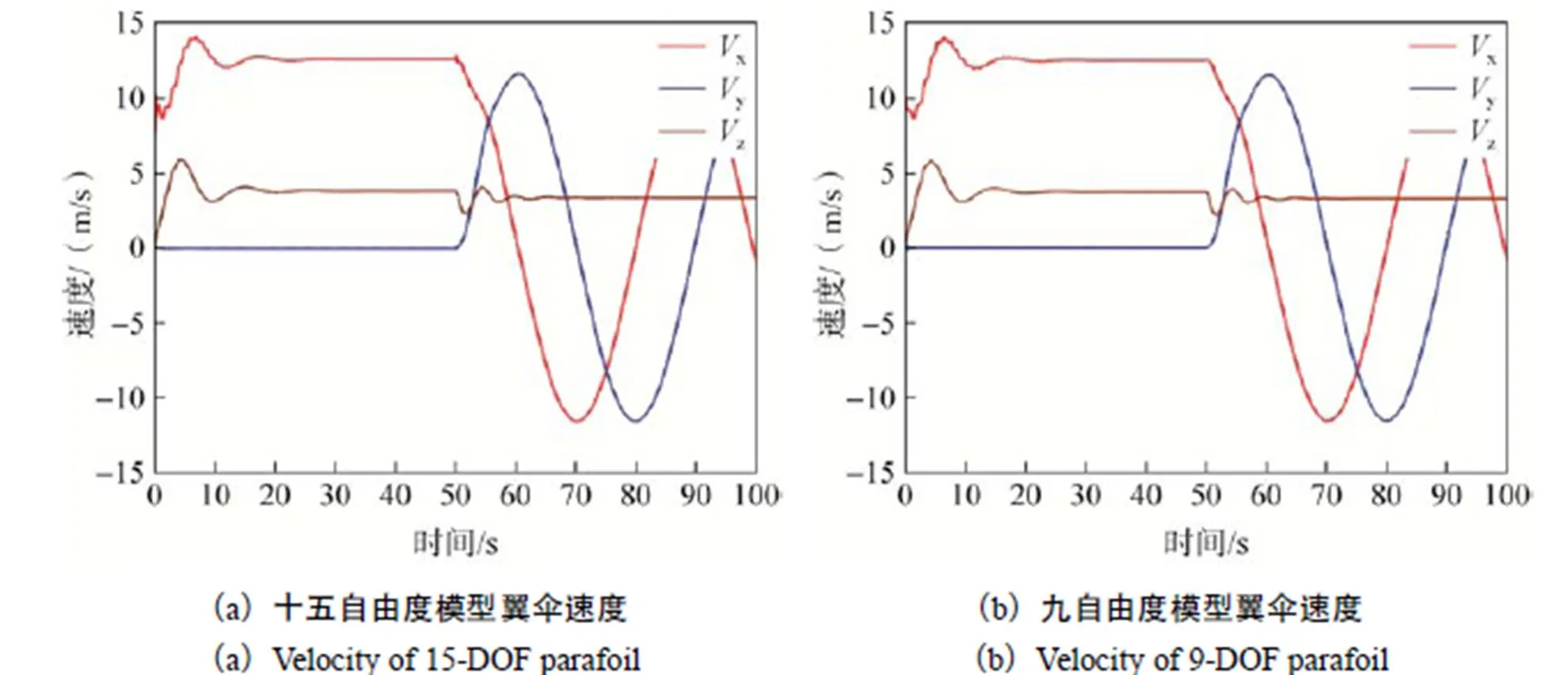
图4 翼伞运动速度

图5 翼伞运动攻角
2.2 连接点c相对伞体运动情况
翼伞在运动过程中伞绳的连接点c相对于伞体会产生微小位移,位移与力cd的大小和相对于伞体的方向相关。如下图6所示为c点位移在伞体坐标系下的值。从图中可以看出,翼伞在滑翔过程中,在p方向上的位移Δcpy接近于0,在p方向上的位移Δcpz最大,约为26cm,p方向上位移Δcpx约为6cm。当翼伞受到单侧下偏控制后,p方向相对位移减小,p方向相对位移增加,p方向的相对位移极小。

图6 连接点相对运动
2.3 吊带运动情况
翼伞与载荷通过伞绳与吊带连接,在翼伞运动过程中吊带能够自由转动,且吊带本身具有弹性,在受到拉力后会产生一定的伸长。吊带的姿态通过地面坐标系下的方向角余弦值表示,如下图7所示。当翼伞处于滑翔过程中,吊带与e方向夹角为90°,与e轴夹角接近为0°,与e轴夹角约为88°。在对翼伞施加下偏控制后,吊带与e方向夹角接近于0°,与e、e的夹角呈周期性变化,吊带的转动会使翼伞与载荷产生相对平移。如图8所示吊带受到拉力后会产生相应的延长,拉力的变化伸长量会有所改变,拉力的震荡导致伞舱高度发生震荡。

图7 吊带运动图

图8 吊带伸长量
3 结论
本文利用翼伞九自由度与十五自由度模型动力学动力学模型进行仿真,研究分析了翼伞的运动特性,以及安装角对于翼伞运动特性的影响。得出以下结论:
1)九自由度模型应用普遍,是目前通用的准确性较高的动力学模型,通过与九自由度模型对比可以得出十五自由度模型的运动情况与九自由度模型基本一致,能够确定十五自由度模型是准确的,可以将该建模应用于翼伞动力学分析。但十五自由度模型较为复杂,在精度要求不高的情况下,可以采用九自由度模型。
2)与九自由度模型相比,十五自由度模型能够更加全面地反映翼伞运动情况,除了整体运动以外,还能够反映伞绳连接点相对于翼伞的运动,以及吊带的运动情况。
3)由于翼伞的十五自由度模型考虑了材料的弹性,可以研究不同的制作材料对翼伞飞行性能的影响。
4)翼伞十五自由度模型能够通过改变吊带长度而改变伞舱高度,与实际应用情况更加吻合。
[1] 熊菁, 宋旭民, 秦子增. 翼伞系统两体相对运动分析[J]. 航天返回与遥感, 2004, 25(2): 10-16. XIONG Jing, SONG Xuming, QIN Zizeng. Study on Relative Motion of Two-body Parafoil System[J]. Spacecraft Recovery &Remote Sensing, 2004, 25(2): 10-16. (in Chinese)
[2] 熊菁. 翼伞系统动力学与归航方案研究[D]. 长沙: 国防科技大学博士学位论文, 2005. XIONG Jing. Research on Dynamics and Homming Control of Parafoil System[D]. Changsha: National University of Defense.
[3] VISHNYAK A. Simulation of the Payload-parachute-wing System Flight Dynamics[C]//Aerospace Design Conference, 2013.
[4] YAKIMENKO O A. On the Development of a Scalable 8-DOF Model for a Generic Parafoil-payload Delivery System[C]//18th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, Munich, Germany. AIAA 2005-1665.
[5] PILLASCH D W, SHEN Y C, VALERO N. Parachute/Submunition System Coupled Dynamics[C]//8th Aerodynamic Decelerator and Balloon Technology Conference, Hyannis, MA, U.S.A. AIAA 84-0784.
[6] WISE K A. Dynamics of a UAV with Parafoil under Powered Flight[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit, 2013.
[7] BARROWS T M. Multibody Parafoil Model[C]//AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, 2013.
[8] PRAKASH O, ANANTHKRISHNAN N. Modeling and Simulation of 9-DOF Parafoil-payload System Flight Dynamics[J]. Aiaa Journal, 2013.
[9] SLEGERS N, GORMAN C. Comparison and Analysis of Multi-body Parafoil Models with Varying Degrees of Freedom[C]// Dissertations & Theses - Gradworks, 2006.
[10] EDWARD J, FALLON II. Parachute Dyanmics and Stability Analysis of The Queen Match Recorvery System[C]//11th Aerodynamic Decelerator Systems Technology Conference, 2003.
[11] GORDON S, LARS W. Analysis of the Relative Motion a Parafoil-load-system[C]//AIAA Aerodynamic Decelerator Systems Technology, 2013: 146-154.
[12] BARROWS T. Apparent Mass of Parafoil with Spanwise Camber[J]. Journal of Aircraft, 2013, 39(3): 445-451.
[13] LINGARD J S. Precision Aerial Delivery Seminar Ram-air Parachute Design[J]. Proceedings of Aiaa Aerodynamic Decelerator Systems, 1995.
[14] PRALASH O, ANANTHKRISHNAN N. Modeling and Simulation of 9-DOF Parafoil-Payload System Flight Dynamics[J]. Aiaa Journal, 2013.
[15] BROWN G. Parafoil Steady Turn Response To Control Input[C]//Aerospace Design Conference, 1993, 208(Pt 10): 1867-1876.
[16] PRSKASH O M, ANANTHKRISHNAN N. Modeling and Simulation of 9-DOF parafoil-Payload System Flight Dynamics[C]//AIAA Atmosphere Flight Mechanis Coference and Exhibit, 2006.
(编辑:刘颖)
Modeling and Simulation of 15-DOF Parafoil Dynmics
YANG Haipeng HE Weiliang
(Beihang University, Beijing 100191, China)
Dynamic modeling is the basis of aircraft design. As a new-type flexibile aircraft, Parafoil has been investyateed many works, but still have a lot of problems. The main parafoil dynamics model includes 6-degree of freedom (DOF) and 9-DOF. The 6-DOF regard parafoil and payload as a complete rigid, parafoil and payload is joint by rigid connection; 9-Dof regard parafoil and payload as relative independent rigid, parafoil and payload joint by pin connection. Both of dynamic models ignore the flexibility of parafoil, and can not reflect the real motion of parafoil. This paper based on parafoil recorvery system assumes that parafoil and ropeare linked by hinge, and regards the rope as elastic road, the strap and load are linked also by elastic road. Finally we build parafoil 15-DOF model. On the one hand we consider the relative motion of junction point of rope, on the other hand we consider the relative of payload. Then we analysis turning flight states of the 15-DOF parafoil. The conclusion indicates that the 15-DOF model is more accurate and comprehensive to reflect the motion of parafoil curtained with 9-DOF model. Besides that, it can also explain the motion of sling and intersect poin of rope.
dynamics model; simulation; 15-degree of freedom; parafoil
V525
A
1009-8518(2018)01-0045-08
10.3969/j.issn.1009-8518.2018.01.006
杨海鹏,男,1992年生,2015年获大连理工大学飞行器设计与工程专业学士学位,现在北京航空航天大学宇航学院攻读硕士学位。研究方向为飞行器设计、翼伞动力学分析。E-mail:18842686749@163.com。
2018-01-04

