一种QPSK短时数据辅助解调方法*
孙宇明,李 铀,朱 倩
0 引 言
随着FPGA设计周期的缩短,逻辑程序编写和硬件设计往往并行进行。因此,利用仿真验证设计的有效性成为一种重要手段,且设计过程中对标准输入信号源正确性的鉴定也是一种有效手段。通过行为仿真对逻辑设计进行系统仿真,并记录输出数据再进行分析,是对此类设计进行验证的常用手段[1-3]。锁相环等存在收敛时间,而常规的接收机同步技术都对序列长度有一定的要求[2-4]。因此,需要通过特殊的算法对短时信号进行处理,以解调出数据,验证其正确性。同时,认知无线电的应用,促使突发通信模式得到广泛应用,进而产生了对短序列的数字解调问题[5-7]。
全数字的接收机是将数字信号的解调全部采用数字处理技术来实现[8-10]。经典载波同步算法需要使用鉴频器或鉴相器对频率或者相位进行鉴别,再通过环路滤波器操作频率或者相位控制字对NCO进行操作[11-12]。经典符号同步算法需要使用定时误差估计算法,如gardener算法等[2]。随着硬件计算能力的增强,通信的计算瓶颈不断被打破,未来通信的瓶颈将是匮乏的频谱资源问题,而突发通信模式是有效节省频谱资源的有效手段。然而,常规算法的性能无法满足此情况下的数据解调需求。
因此,本文提出了一种相位调制短时数据辅助解调方法,解决了短时QPSK数据解调问题。该算法充分利用发射信号中的全部信息,对信号的载波和符号定时位置进行估计,然后再对其进行解调。仿真结果表明,在高斯白噪声信道下,新算法的载波同步精度和定时同步精度均高于传统算法。
1 系统模型
假设接收到一帧QPSK调制数据,且下变频后的数据为y[k]:
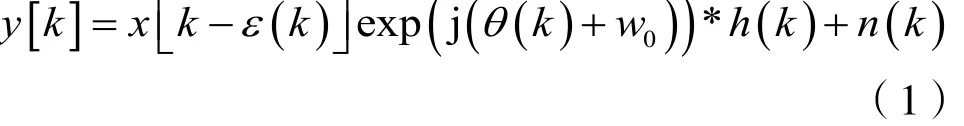
h(k)表示信道传输参数;n(k)表示加性高斯白噪声,ε(k)表示未知的时钟相位抖动,θ(k)是未知的载波相位,w0表示载波中心频率。
2 已有算法
由文献[2]可知,鉴相使用科斯塔斯鉴相器,符号同步采用gardener算法,算法如式(2)所示。利用序列进行估计后前向纠正,完成解调。
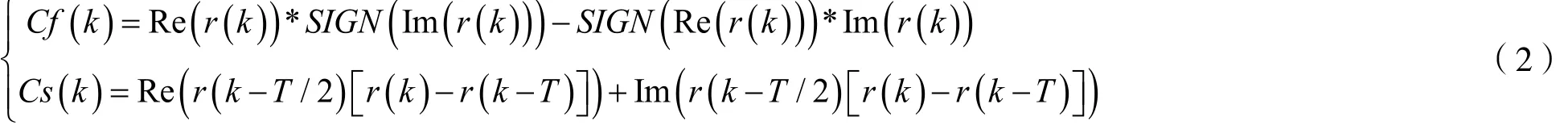
式中,Re表示复数的实部,Im表示复数的虚部,SIGN表示取符号位,T表示符号周期,Cf(k)表示频率控制估计结果,Cs(k)表示符号定位结果,r(k)表示接收下变频后数据。
3 新算法
频率估计公式为:
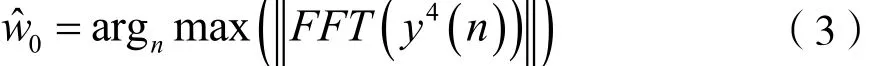
式中,arg max表示最大值处的位置。由于成形滤波器和高通滤波器等因素,发射调制信号的相位并不一定是按照正弦波相位的分布方式分布。因此,将该相位形成的序列称为相位序列。
相位同步序列估计公式为:
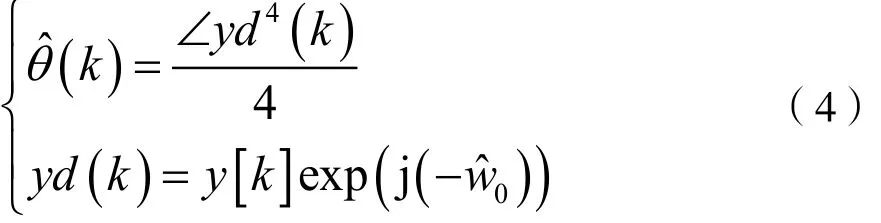
式中,yd(k)表示下变频后带有相位残差的信号。则最后解调后信号为:
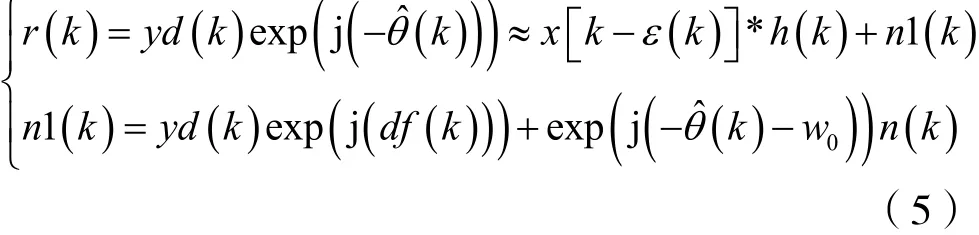
为提高接收性能,需降低n1(k)能量。对于相位调制而言,就是降低相位估计误差引起的噪声df(k)。对df(k)进行分析:

式中,Δf为频率估计偏差,Δφ为相位估计偏差。在理想情况下,Δf估计误差与信噪比成正比,与变换点数成反比。对于至少10 000点的观测量而言,频率估计误差可以忽略,认为是准确的。因此,只要分析Δφ即可。由于信号源都是使用DDS产生的,频率合成的概念是在平均的意义上合成相应的频率,因此会产生一定的相位抖动。将相位抖动加入估计序列,对系统系统性能也有一定的提高作用。而采用数据迭代的方式将解调数据重新迭代,这样能够获得更准确的估计结果。
符号定时频率偏差估计方法为:

改变采样率,插值滤波算法为:

式中,n是原序列序号,k是新的序列序号,hI是插值滤波器系数,长度是N1+N2。
定时位置估计位置为:

式中,arg max表示区间最大值位置。
获得的最佳采样值积分集合点序列为:

使用数据补偿后,用ML算法估计频率差,如下:

式中,Ni表示插值数据个数,Xb表示经过数据补偿后的最佳采样点序列。
综上,新算法的实现步骤如下:
(1)使用式(3)对序列进行频偏估计,估计精度为[-fs/2N, fs/2N];
(2)使用式(4)对序列进行相位差估计;
(3)对接收序列进行相位差补偿,并进行低通滤波,然后使用式(7)进行符号同步采样频差估计,并对序列进行采样率变化。将采样率按照式(8)变为符号速率的整数倍,然后根据系统性能要求,选择全数字插值滤波器的类型和系数。
(4)利用式(10)估计最佳采样点积分起始位置,并积分;
(5)对最佳采样点进行星座图映射,解调出第一次初始数据;
(6)按照式(11)对残余频偏进行扫频,估计精度为N/64,并将估计结果在此补偿到接收序列;
(7)补偿后序列重复步骤(2)开始的工作,直至式(11)的估计结果两次之差满足要求为止。
4 算法仿真和实验
在高斯白噪声信道下,利用蒙特卡罗法分别对新算法和仅使用常规算法进行行为仿真。
仿真参数如下:
(1)QPSK系统带宽为3.14 MHz,信道多普勒等其他因素引起的频率偏移为4.98 kHz,中频频率为50.24 MHz,中心频率为12 MHz;
(2)复数基带信号从QPSK星座点中随机选取,成型滤波器选用升余弦滤波器,滚降系数为0.5,采样值采取12 bit量化,峰峰值为1 024;
(3)每帧数据长度为1 ms,即50 240个点,
3 140个符号。
(4)插值滤波器拉格朗日三次多项式插值;
(5)发射信号分别经过高斯白噪声信道;
(6)在0~40 dB信噪比下,对上述两种算法进行仿真,计算定时估计均方差和频偏估计均方差,并且观测星座图。对于短时突发信号,信噪比一般比较理想,因此选用20 dB观测星座图。
仿真结果表明,在加性高斯白噪声信道下,新算法比常规算法的频偏和定时估计精度高,星座图收敛明显。如图1所示,在高斯白噪声信道下,当信噪比相同时,新算法的频偏估计均方误差优于传统算法10倍以上;如图2所示,在高斯白噪声下,定时精度也优于传统算法;从图3则可看出,新算法的星座图收敛明显。

图2 定时估计性能比较

图3 星座图比较
5 结 语
本文提出了一种相位调制短时数据辅助解调方法。该算法充分利用发射信号中的解调数据,对信号载波和符号定时位置进行估计,然后再对其进行解调。仿真结果表明,在加性高斯白噪声信道下,新算法比常规算法的频偏和定时估计精度高,且星座图收敛明显。
[1] 张公礼.全数字接收机理论与技术[M].北京:科学出版社,2005:10-20.ZHANG Gong-li.All-digital Receiver Theory and Technology[M].Beijing:Science Press,2005:10-20.
[2] 尹长川,罗涛,乐广信.多载波宽带无线通信技术[M].北京:北京邮电大学出版社,2004:22-69.YIN Chang-chuan,LUO Tao,LE Guang-xin.Multicarrier Broad-band Wireless Communication Technology[M].Beijing:Beijing University of Post and Telecommunications Press,2004:22-69.
[3] 黄仁亮.OFDM系统原理及仿真实现[J].信息安全与通信保密,2009,34(08):77-80.HUANG Ren-liang.Security Risk Assessment of Network Management System[J].Information Security and Communications Privacy,2009,34(08):77-80.
[4] 王晓芳,王晓斌,金明录.认知无线电中一种改进的频谱感知算法[J].通信技术,2011,44(09):8-12.WANG Xiao-fang,WANG Xiao-bin,JIN Ming-lu.An Improved Spectrum Sensing Algorithm in Cognitive Radio[J].Communications Technology,2011,44(09):8-12.
[5] 刘思洋,高俊,刘全.基于认知无线电的军事电磁频谱管理研究[J].通信技术,2011,44(12):37-41.LIU Si-yang,GAO Jun,LIU Quan.Study on Military Communication Spectrum Management Based on Cognitive Radio[J].Communications Technology,2011,44(12):37-41.
[6] GUO Y,LIU G,GE J.A Novel Time and Frequency Synchronization Scheme for OFDM Systems[J].IEEE Transactions on Consumer Electronics,2015,54(02):321-325.
[7] FUSCO T,TANDA M.Blind Synchronization for OFDM Systems in Multipath Channels[J].IEEE Transactions on Wireless Communications,2016,8(03):1340-1348.
[8] YOU Y,LEE K,KANG S.Pilot-aided Frequency Offset T-racking Scheme for OFDM-based DVB-T[J].IEEE Transactions on Consumer Electronics,2017,54(03):1053-1058.
[9] SHI K E,SERPEDIN E,CIBLAT P.Decision-directed Fine Synchronization in OFDM Systems[J].IEEE Transactions on Communications,2015,53(03):408-412.
[10] SCHIMDL T,COX D.Robust Frequency and Timing Sync-hronization for OFDM[J].IEEE Transactions on Co mmunications,2016,45(12):1613-1621.
[11] CHOI J,LEE Y.Optimum Pilot Pattern for Channel Estimation in OFDM Systems[J].IEEE Transactions on Communications,2017,4(05):2083-2088.
[12] 孙宇明,赵鹏,王青等.基于迭代的FH-OFDM小数倍频偏估计算法[J].通信技术,2013,46(06):76-79.SUN Yu-ming,ZHAO Peng,WANG Qing,et al.A Fractional Frequency Estimation Algorithm for FHOFDM System Based on Iteration[J].Communications Technology,2013,46(05):76-79.

