集美区机动车路网复杂度评价分析

， ， ， ，

(1.福建农林大学 交通与土木工程学院， 福建 福州 350002； 2.厦门大学 嘉庚学院， 福建 厦门 363105)

复杂网络是将大量的数据真实反映出来的抽象系统，能有效表征内部各因素的交互关系[1]。将城市道路作为复杂网络进行研究，可有效分析路网的特点，明确现状路网存在的问题，以及未来路网建设应着重发展的方向。为了更好地规划集美区道路网，研究以集美区路网的复杂度为切入点，分析集美区总体及各片区路网的建设情况。

目前对路网复杂度的研究较多元，高自友等通过研究城市公交网络的无标度特性和度分布指数甄别公交枢纽站点[2]。张勇等引入网络平均距离、节点度分布以及簇系数等概念，研究了城市路网映射后的复杂网络特征[3]。马杰等运用数据建模的方式对江苏省公路网络进行分析并评价其可靠性[4]。刘承良等运用复杂网络理论揭示了城乡道路网拓扑结构演化及复杂性“涌现”过程[5]。在复杂度指标分析及构建[6-8]、复杂网络应用[9-12]等方面还有很多的研究成果和结论，这些成果为后续的研究提供了理论基础和实践案例。

研究采用对偶法构建集美区总体及各片区机动车路网，选取了节点度及其分布、网络族系数和平均路径距离作为路网复杂度评价指标，并对网

络类型特征进行分析。运用Ucinet、Pajek等软件计算了集美区路网的复杂度指标，通过比较分析获取各路网的网络特性与网络类型，进一步探讨了路网的特征及不足，为集美区后续路网规划和建设提供科学的参考依据。

1 对偶法构建机动车路网模型

将集美区机动车网络运用对偶法转换为一个无向带权网络G=(V,E)(见图1)。令N为节点数、M为边数，将A=(aij)定义为机动车网络邻接矩阵(见图2)，其中若i点和j点相连表示为aij=1，反之为0。同时，将集美区根据地域特征划分为4个片区，分别为杏林片区、灌口片区、北站及后溪片区、以及集美大学城片区。分区研究利于发现区域间差别，为后期路网分区规划提供可靠的基础数据。各片区路网拓扑结构图见图3。

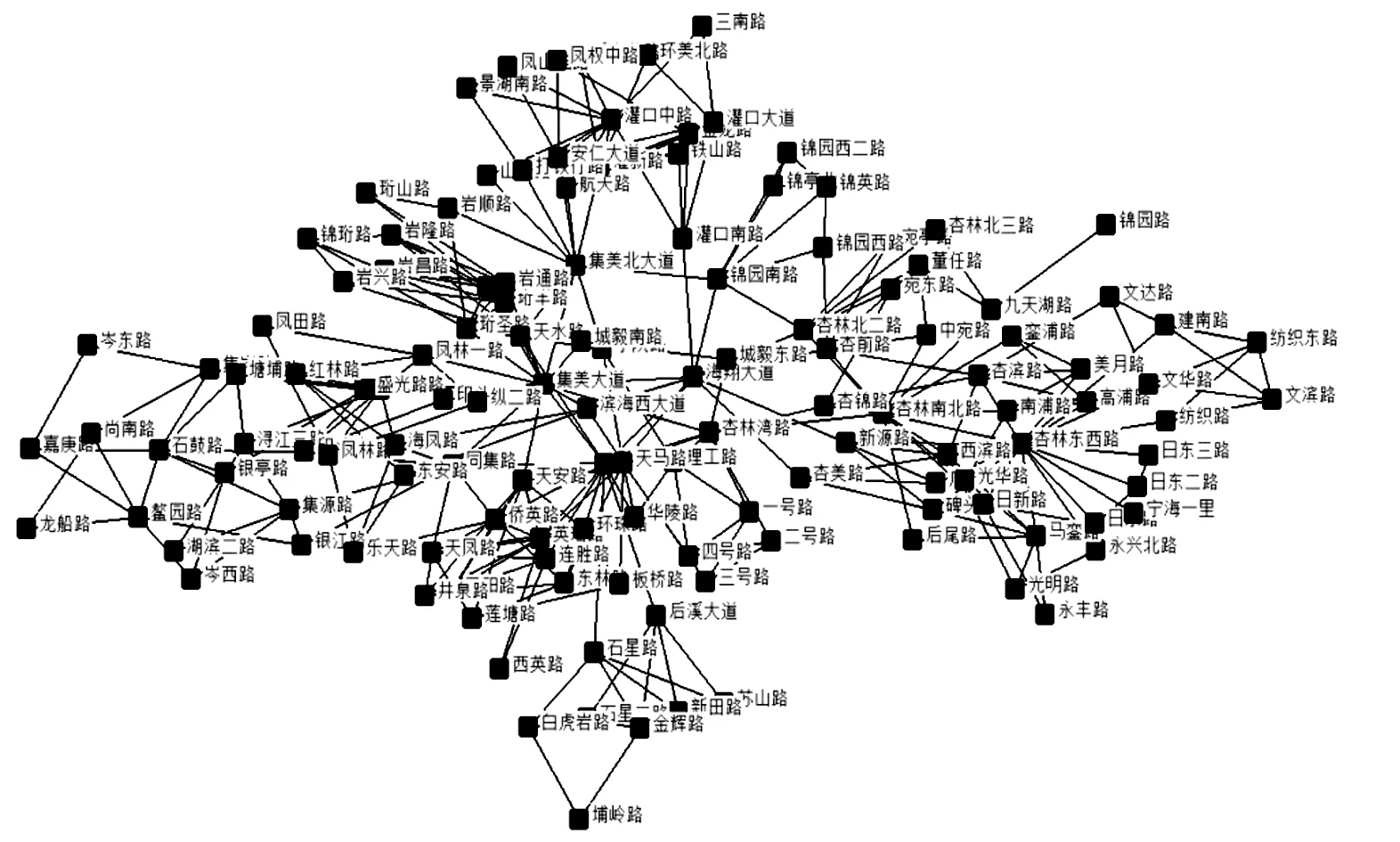
图1 对偶法转换后的集美区拓扑网络Fig.1 Topological network of Jimei District converted by the dual method

图2 集美区机动车网络部分邻接矩阵示例Fig.2 Part of the adjacency matrix of Jimei’s road network

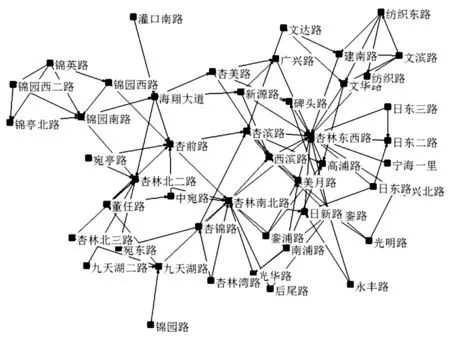
(a)杏林片区

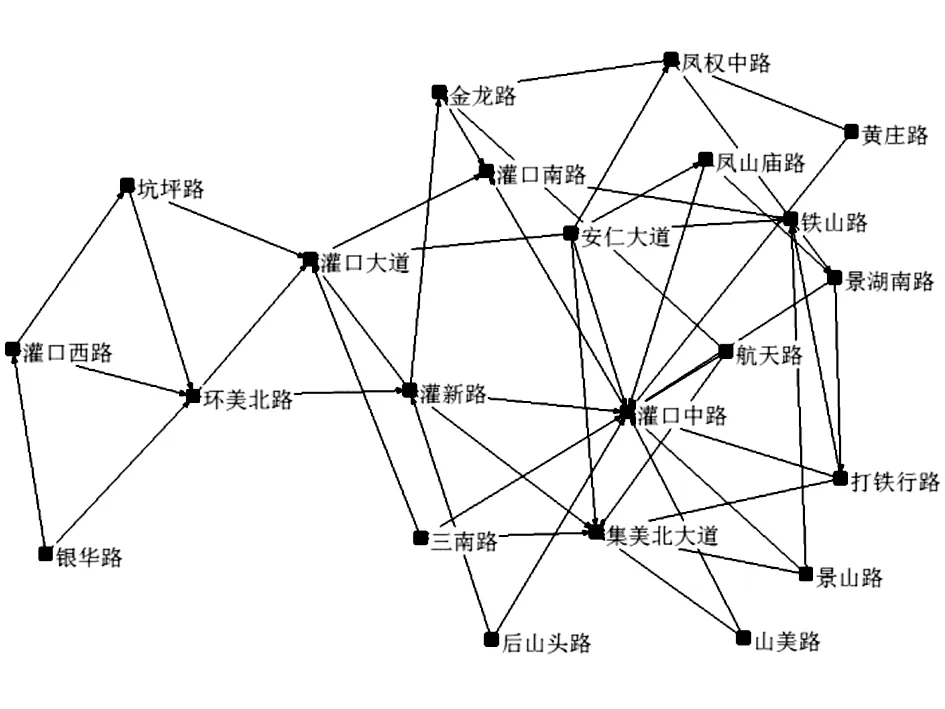
(b)灌口片区

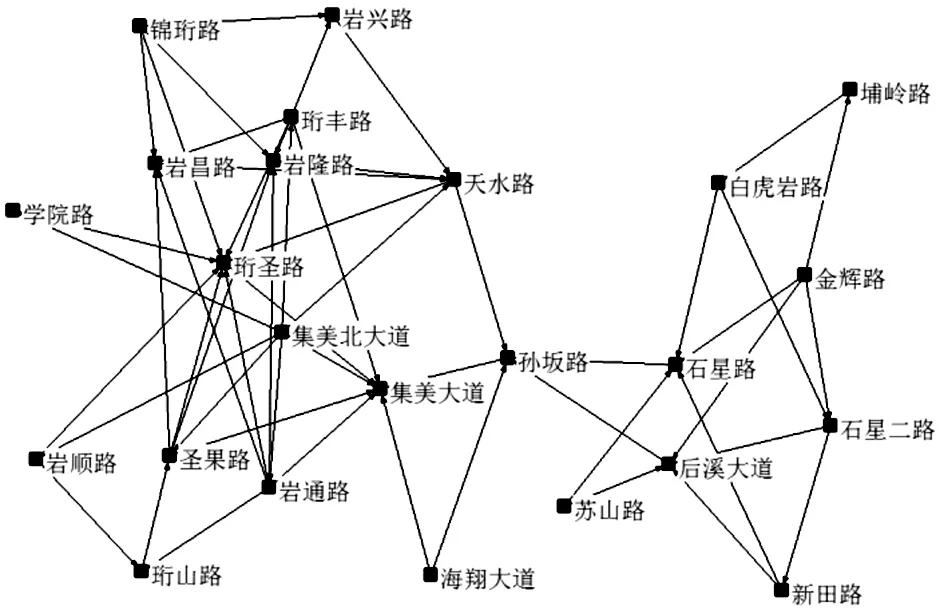
(c)北站及后溪片区

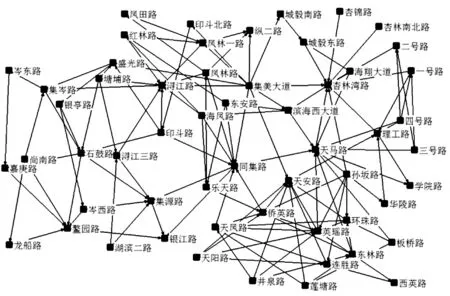
(d)集美大学城片区

2 机动车路网复杂度评价指标

随着城市机动车路网的不断变化，影响其复杂度的因素也越来越大。借鉴文献[1-3,6]，选取以下3个指标作为复杂度计算的关键指标，分别为度和度分布、簇系数以及网络平均路径距离；同时根据这3个指标的计算结果及网络形态，确定不同网络类型的特征，作为后续网络分析的参考标准。

2.1 度和度分布

把对偶网络中节点的总邻边数称作度，第i个节点的度记为ki，其计算公式如下：

ki=∑aij

(1)

式中aij为网络邻接矩阵A中的元素，表示两个节点之间是否存在边。如果aij=1，则表示点i和点j存在边，反之用0表示。

平均节点度表示所有节点度的平均值，即为

(2)

式中：N为所有节点数的总和。

具有同样邻边数的节点的出现概率用分布函数P(k)表示

P(k)=N(k)/N

(3)

式中N(k)为所有度为k的节点个数的总和。

在对偶法转换的机动车路网中，度值反映了道路之间的连接情况，节点度越大说明该节点在网络中重要度越高。

2.2 簇系数

簇系数指的是某个节点与其所有相邻的节点间的实际连接数与可能连接最大数的比值。计算公式如下：

(4)

式中Ci为第i个节点的簇系数；Ei为ki个节点之间实际互相连接数。

在对偶法转换的机动车路网中，簇系数表示与某一条路相交的其他道路之间也互相相交的概率，可反映出机动车路网的聚集程度。

2.3 平均路径距离

网络平均路径距离指所有节点之间的最短路径边数的平均值，计算公式如下：

(5)

式中Lij为节点i到节点j所需要经过的最少边数。

在对偶法转换的机动车路网中，网络平均路径距离体现了网络传输的效率，平均路径距离越小的网络，路网的可达性越好。

2.4 网络类型特征分析

根据各种路网的节点及其之间的边的连接方式的不同，目前主要有4种网络类型：随机网络、无标度网络、小世界网络和规则网络，其主要特征见表1所示。路网类型能有效反应不同路网的结构特性[13]，可为后期路网规划和优化提供特征量度依据。

表1 网络类型及其主要特征Tab.1 Network types and their main features

3 集美机动车路网复杂度评价分析

3.1 路网复杂度指标分析

运用Ucinet软件对集美区总体及分区拓扑网络进行计算，获取各指标数据见表2。

集美区总体机动车路网平均度为4.672，各道路范围节点度分布如图4所示。对各道路范围进行度分布拟合，总体路网和集美大学城片区的拟合度较低，杏林片区和灌口片区符合两种分布情况。

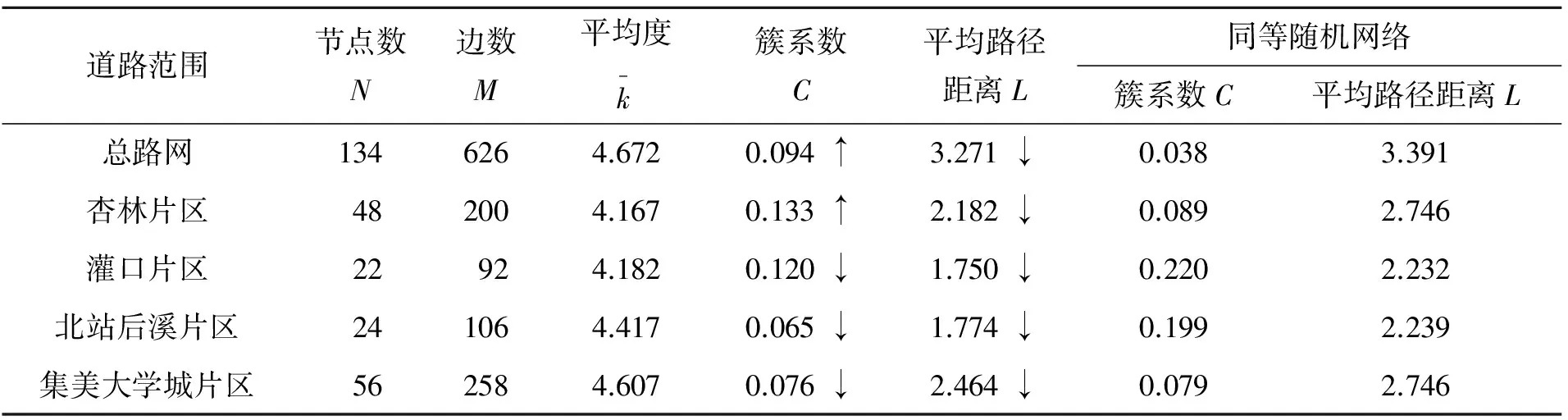
表2 集美区及各片区路网复杂度指标Tab.2 Complexity index of the vehicle road network in Jimei and its four areas

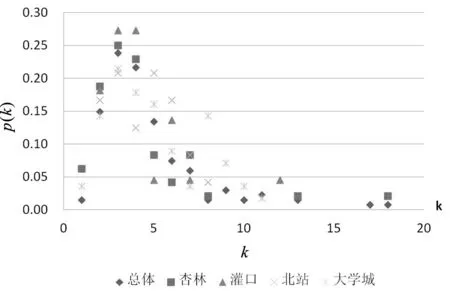
图4 集美区路网节点度分布情况 Fig.4 Node degree distribution of Jimei’sroad network

集美区总体路网簇系数为0.094，说明机动车路网集聚度不高，道路分布较为零散。灌口片区的后山头路、杏林片区的锦亭北路、北站后溪片区的海翔大道、集美大学城片区的龙船路及湖滨二路的簇系数最高，说明这些道路在各片区中影响较大。

集美区机动车路网的平均路径距离L为3.271，说明集美区任意两条道路大概经过3条其他道路可到达。而路网规模和覆盖范围较小的灌口片区和北站后溪片区的网络平均路径距离比其他两个片区小，反应了这两个片区的路网可达性较高。

3.2 集美区路网类型分析

根据统计分析获取的复杂度评价指标，对集美区不同范围路网度分布进行拟合，判定各范围路网类型。具体结果见表3所示。

集美区机动车总路网度分布拟合结果更接近于指数分布，网络平均距离小于同等规模随机网络的数值，且簇系数大于同等规模随机网络，符合小世界网络特征。同理，杏林片区路网也更接近小世界网络。

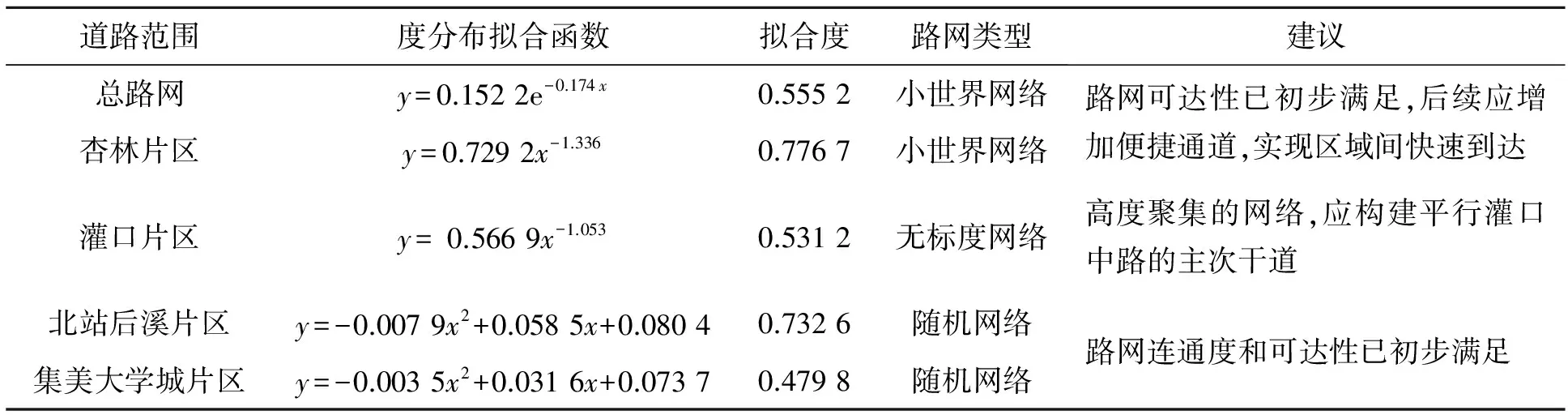
表3 集美区路网类型分析及建议Tab.3 Analysis of Jimei’s road network types and suggestions

灌口片区绝大多数节点的度较少(多集中在2～6)，而灌口中路的度为12，说明其路网连接性高度集中，同时其度分布接近幂指数分布，灌口片区网络平均距离小于同等随机网络，因此，灌口片区路网符合无标度网络特征。

北站后溪片区的簇系数小于相同规模的随机网络，而网络平均距离也小于同等随机网络，节点度分布拟合符合二项分布。集美大学城片区簇系数与同等的随机网络相差无几，且平均路径距离也接近同等随机网络。综上，北站后溪片区和集美大学城片区的路网类型更接近于随机网络。

综上所述，集美区总体及各片区路网类型较为多样，说明不同区域路网结构差别较大，在后续道路网规划及建设中应根据不同片区的路网特征进行分区规划，同时对总体指标进行把控，优化路网密度及连接度，提高路网运行效率。

4 结束语

利用复杂网络研究集美区机动车路网的复杂度，建立评价指标并应用Ucinet、Pajek等软件进行计算分析，明确不同道路范围路网类型及其特点，为后续道路网规划及建设提供参考和建议。在后续研究中，可运用其他方法对路网进行转换，减少因为道路相同名称不同，或者名称相同道路走向不同引起的节点误差，同时也可考虑不同路段的交通量指标[14]，实现路网与实时路况的结合。

[1] 高自友,赵小梅,黄海军，等.复杂网络理论与城市交通系统复杂性问题的相关研究[J].交通运输系统工程与信息,2006,6(3):41-47.

[2] 高自友,吴建军,毛保华，等.交通运输网络复杂性及其相关问题的研究[J].交通运输系统工程与信息,2005,5(2):79-84.

[3] 张勇,杨晓光.城市路网的复杂网络特性及可靠性仿真分析[J].系统仿真学报,2008, 20(2):464-467.

[4] 马杰,曹祥,周旭辉.江苏省公路网络复杂性分析[J].南京信息工程大学学报(自然科学版),2011,3(2):158-163.

[5] 刘承良,段德忠,余瑞林，等.武汉城市圈城乡道路网结构演化及复杂性研究[J].地理科学,2014,34(4):401-410.

[6] 胡一竑.基于复杂网络的交通网络复杂性研究[D].上海：复旦大学,2008.

[7] 刘建国,任卓明,郭强，等.复杂网络中节点重要性排序的研究进展[J].物理学报,2013,62(17):9-18.

[8] 于会,刘尊,李勇军.基于多属性决策的复杂网络节点重要性综合评价方法[J].物理学报,2013,62(2):54-62.

[9] 孙仁诚,邵峰晶.青岛市公交线路网络复杂性分析[J].复杂系统与复杂性科学,2009,6(3):63-68.

[10] 周宏达,陈守刚,杨德刚.主城区公路网的复杂网络特征分析[J].成都大学学报(自然科学版),2009,28(4):342-345.

[11] 刘志谦,宋瑞. 基于复杂网络理论的广州轨道交通网络可靠性研究[J].交通运输系统工程与信息,2010,10(5):194-200.

[12] 田庆飞.基于复杂网络理论的城市公交网络生成与优化研究[D].长春：吉林大学,2013.

[13] 许峰,毛钢,秦臻.复杂网络特征量度及典型网络模型分析[J].通信技术,2010,9(43):112-114.

[14] 何兆成,庄立坚,杨文臣，等.基于大规模浮动车数据的城市道路网复杂度分析[J].公路交通科技,2013,30(6):120-126.