基于改进SPEA2算法的给水管网多目标优化设计

孟勤超，杨翠丽，乔俊飞

（1. 北京工业大学 信息学部，北京 100124; 2. 北京工业大学 计算智能与智能系统北京市重点实验室，北京 100124）

给水管网是城市重要基础设施，是整个城市得以生存和发展的命脉[1]。同时，给水管网投资巨大，往往占到整个供水系统的60%～80%，而且还涉及庞大的运行动力费和运行管理费[2]。

给水管网的优化设计，一般是在工程资金投入有限的情况下，寻求满足用户用水需求，且使整个系统的造价最低可靠性最高的设计方案。因此，管网的优化设计直接影响到整个供水系统的经济性和可靠性[3]。由于管网系统的非线性和管径的离散性，管网的多目标优化求解十分困难，成为了国内外众多学者研究的热点问题。文献[4]第一个将结构化混合遗传算法(structured messy genetic algor-ithm, SMGA)应用到给水管网多目标优化中，并将系统造价最低、收益最大作为两个目标，求得了一系列非支配解，但是SMGA算法的求解效率和所得解的多样性较差。文献[5]建立了以管网造价最小、管网压降最小为目标的优化模型，并采用多目标粒子群算法(multi-objective particle swarm optimization algorithm, MOPSO)进行优化，但是MOPSO算法不适合离散变量的优化问题。文献[6]建立了以管网造价最小、水质最优为目标的优化模型，且采用多目标遗传算法(multi-objective optimization genetic algorithm, MOGA)进行管网优化设计，其研究的重点主要为管网模型的设计。文献[7]以管网造价最低、可靠性最高为目标，建立了3个目标的管网优化模型，并采用快速非支配排序遗传算法(nondominated sorting genetic algorithm II, NSGA-II)优化管网模型，取得了较好的效果，但是NSGA-II算法容易陷入局部最优，使获得的解分布不均匀。

目前，智能优化算法在解决管网多目标优化问题中取得了广泛的应用，但解的多样性和收敛性不好是其存在的主要问题，因此提高多目标优化算法解的多样性和收敛性成为重要的研究方向[8-10]。文献[11]提出了强度帕累托进化算法(strength Pareto evolutionary algorithm 2, SPEA2)，通过引入密度估计策略和归档集截断算法，从一定程度上提高了算法解的多样性和收敛性。文献[12]提出的NSGAII算法，其快速非支配排序和拥挤距离策略提高了多样性和收敛性。这两种算法均能从一定程度上提高算法的性能，但是都将多目标优化问题作为一个整体优化。因此当目标数大于2时，这两种算法的搜索性能急剧下降。文献[13]提出了基于分解的多目标进化算法(multi-objective evolutionary algorithm based on decomposition, MOEA/D)，将一个多目标优化问题分解为多个单目标优化问题，通过同时优化所有的单目标子问题，提高了算法解的多样性和收敛性。但是，对于具有不同Pareto前沿的多目标优化问题，MOEA/D却使用了相同的权值向量。文献[14]基于支配和分解的框架，在NSGA-II算法基础上，结合一组提前设定的参考点，提出了NSGAIII算法。虽然NSGA-III算法进一步提高了解的多样性和收敛性，但是其收敛速度依然较慢，而且固定的参考点使得具有不同Pareto前沿的多目标优化问题难以达到相同的优化效果。

本文采用SPEA2算法[11]作为基础，结合NSGAIII中基于支配和分解的思想，提出了一种基于参考向量的强度帕累托进化算法(strength Pareto evolutionary algorithm 2 based on reference vectors, RVSPEA2)，其目的是提高算法的多样性和收敛性，并采用文献[7]的3个目标作为管网优化模型，将其应用到双环管网、纽约管网以及实际的管网优化案例中。

1 给水管网优化模型描述

给水管网优化设计的目的是在满足用户用水需求的前提下，使管网经济性最低和可靠性最高，并求出最优管线直径。本文中采用管网造价作为经济性目标，节点富余水头总和与节点富余水头方差作为可靠性目标，建立给水管网优化模型。

1.1 目标函数

为了简化管网优化计算，本文采用管网造价作为经济性目标，其目标函数如式(1)：

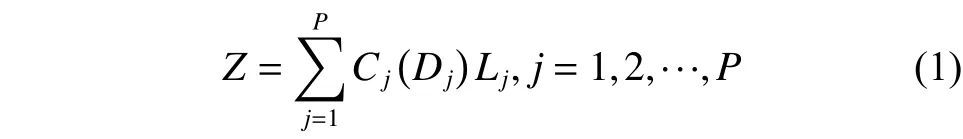
式中：Z为管网总造价；Dj、Lj分别为第j根管段的直径、长度；Cj(Dj)为管径为Dj的管段的单位长度造价；P为管网中管段总数。

管网的可靠性目标可用节点富余水头总和与节点富余水头方差表示。其相关定义如下。

每个节点的富余水头Isi计算如式(2)：

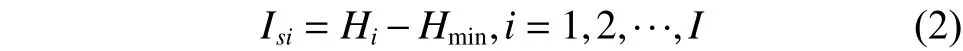
式中：Hi为管网节点i的水压标高；Hmin为管网节点所要求的最小自由水压；I为管网中节点总数。

给水管网节点富余水头总和Is为

节点富余水头均值Is为

节点富余水头方差S为

因此，给水管网多目标优化模型可表示为

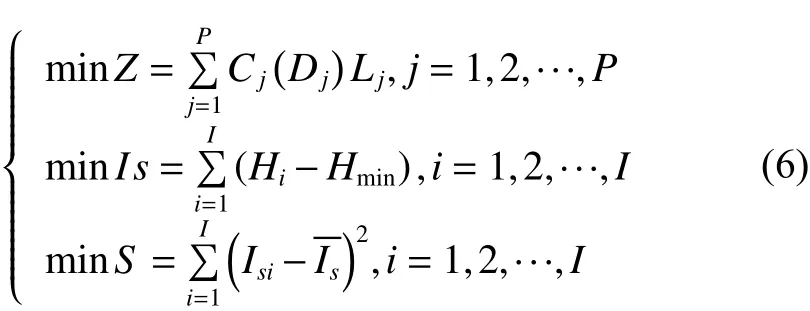
管网总造价Z越小，表明管网系统经济性越高。节点富余水头Is是指节点自由水头超过节点所要求的最小自由水头的部分水头，它与管网水压呈线性关系。在满足管网约束的条件下，节点富余水头越小，管网水压就越低。节点富余水头总和越大，即管网水压总和越大，一方面反映了资源浪费的情况，另一方面也代表了管网存在爆管的危险。另外，节点富余水头方差S反映了管网中各节点富余水头的分布情况。节点富余水头方差越大，说明了管网中各节点压力分布不均，亦存在爆管的危险。因此，节点富余水头总和与节点富余水头方差越小，表明管网系统可靠性越高。

1.2 约束条件

除了优化目标之外，给水管网的优化还必须满足下列约束条件。

1) 节点流量连续性约束管网中每个节点应满足：

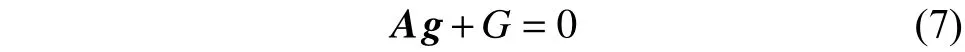
式中：A为节点关系矩阵，g为与该节点相连的管段流量，G为节点流量。

2) 能量平衡约束

管网中闭合回路水头损失代数和为零，即

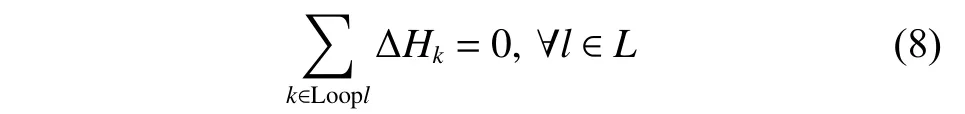
式中：ΔHk为闭合回路l中管段k的水头损失，L是管网中所有闭合回路。

3) 节点流量连续性约束

管网中每个节点应满足

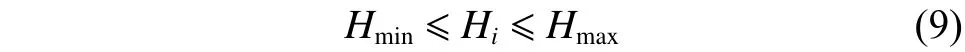
式中：Hi为节点i的水头，Hmin和Hmax分别为节点最小水头和最大水头。

4) 能量平衡约束

管网中每个管段直径应满足：

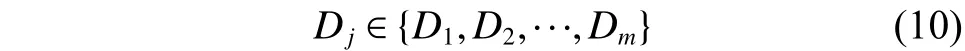
式中：Dj为管段j的直径，D1～Dm为标准管径。

2 基于参考向量的强度帕累托进化算法RVSPEA2

本文基于SPEA2算法，与基于支配和基于分解的选择机制相结合，提出了一种基于参考向量的强度帕累托进化算法(RVSPEA2)，旨在进一步提高算法解的多样性和收敛性，以解决给水管网的多目标优化问题。

2.1 基于参考向量的选择机制

在SPEA2算法的环境选择过程中，当前种群中所有的非支配解被放入外部归档集中。如果外部归档集|Qt|≥N(预设值)，则通过最小距离截断算法删除个体，直至|Qt|=N；如果外部归档集|Qt|＜N(预设值)，则随机选择支配解放入外部归档集，直至|Qt|=N。而在RVSPEA2中，当外部归档集|Qt|＜N时，引入参考向量，根据非支配解与参考向量的关系，有目标地选择支配解放入外部归档集，其选择机制将在本节中详细介绍。

2.1.1 自适应目标归一化

在实际的多目标优化问题中，各目标的范围往往差别很大，其对优化结果影响巨大[15]。因此，为了解决目标范围不同的优化问题，RVSPEA2采用了一种简单的目标归一化方法，即对于第j代种群的第i个目标函数 fi,j(x)，其归一化如式(11)：

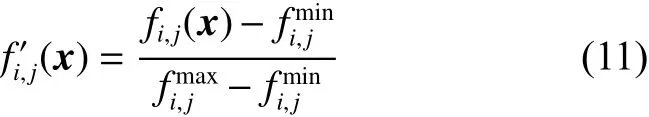
2.1.2 参考向量的生成

为了探索和开发整个搜索空间，RVSPEA2采用了一种简单且有效的方法用于生成参考向量。首先，在整个归一化目标空间生成Km个参考点，其中m为目标个数，K的计算公式如式(12)：

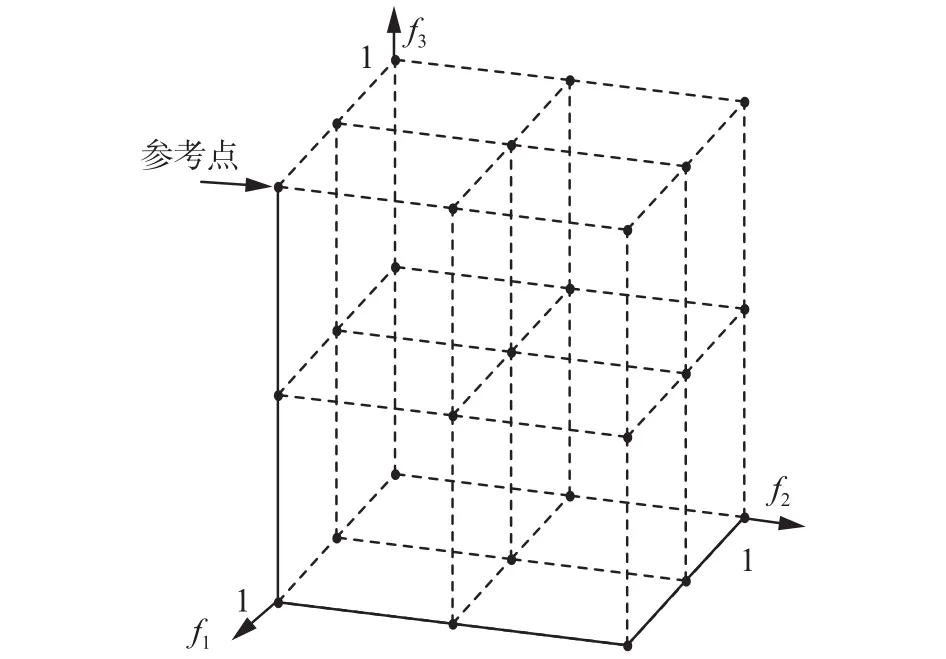
图 1 当m=3，K=3时归一化空间中的27个参考点Fig. 1 Twenty-seven reference points on the normalized objective space for a three-objective problem with K=3

2.1.3 关联操作

生成参考向量后，将种群中每个成员都关联一个参考向量。首先，计算种群成员与每一个参考向量的垂直距离，如式(13)所示。与每个成员垂直距离最近的参考向量将与该成员相关联，如式(14)：

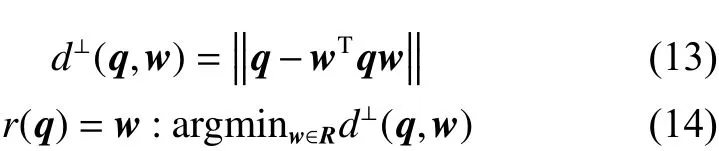
式中：q 为种群成员，w 为参考向量，d⊥(q;w)代表q 与w 的垂直距离，∥·∥代表向量的模，R 为参考向量集合，函数argmin 可计算出当目标函数d⊥(q;w)最小时的变量值w。

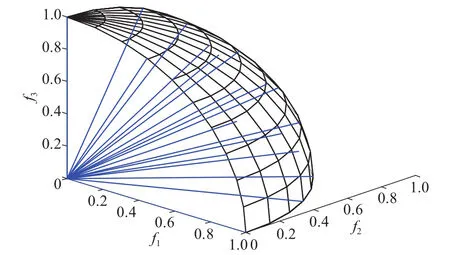
图 2 当m=3，K=3时归一化空间中的参考向量Fig. 2 Reference vectors on the normalized objective spacefor a three-objective problem with K=3

2.1.4 环境选择操作

经过关联操作后，一个参考向量可能会有一个或多个种群成员与之相关联，甚至没有种群成员与之相关联[16]。当外部归档集|Qt|＜N时，通过统计已有成员所关联的参考向量，排除这部分参考向量，从剩余参考向量所关联的种群成员中选择成员填满外部归档集。当外部归档集|Qt|≥N时，则依然通过最小距离截断算法删除个体[6]，直至|Qt|=N。通过参考向量选择可以保证算法初期优化解的多样性，避免算法陷入局部最优；而在算法后期，在保证算法收敛性的同时，通过最小距离截断算法，进一步提高算法的多样性。

2.2 算法流程及性能测试

设种群大小为N，最大进化代数为T，RVSPEA2算法的具体流程如下：

1) 初始化种群P0和外部归档集Q0，进化代数t=0；

2) 合并 Pt和 Qt为 Qt+1；

3) 计算种群Qt+1中各成员的适应度；

4) 通过选择机制，从Qt+1中选出N个成员；

5) 进行锦标赛选择配对、单点交叉和均匀变异操作，得到Pt+1；

6) 计算t=t+1，并判断算法的终止条件，若满足则进行下一步，否则转至2)；

7) 通过选择机制选出N个非支配解，并输出结果。

为了验证算法的性能，将RVSPEA2算法与SPEA2、NSGA-II和MOEA/D进行对比，用于优化双环管网和纽约管网，其布局图分别如图3和图4所示，其节点水压和管段长度等详细数据参照文献[17]。为了比较算法所得解的多样性和收敛性，本文采用了以下3个性能指标。

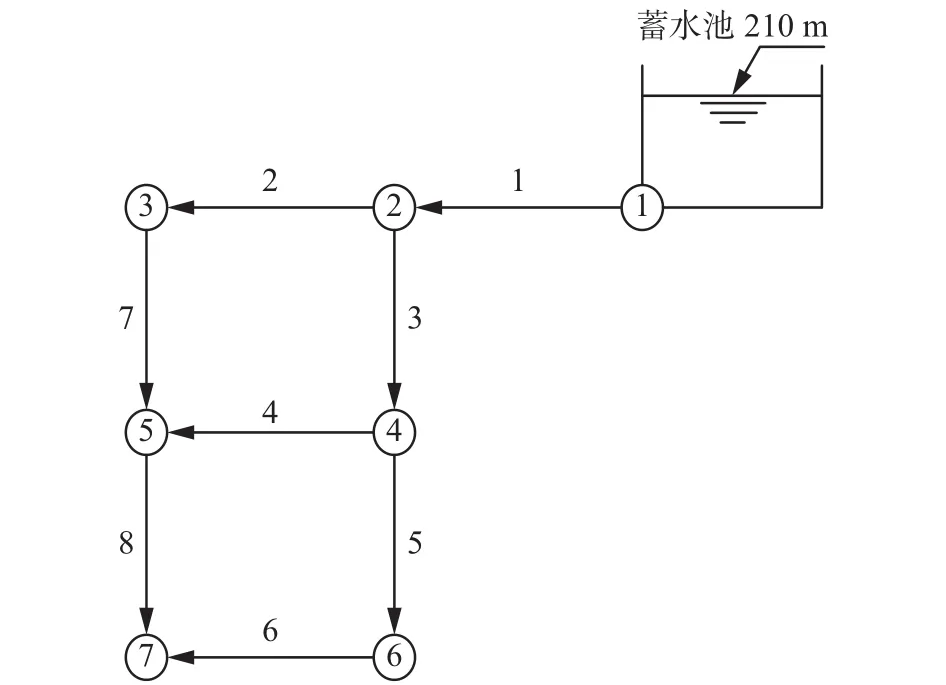
图 3 双环管网Fig. 3 Two-loop network

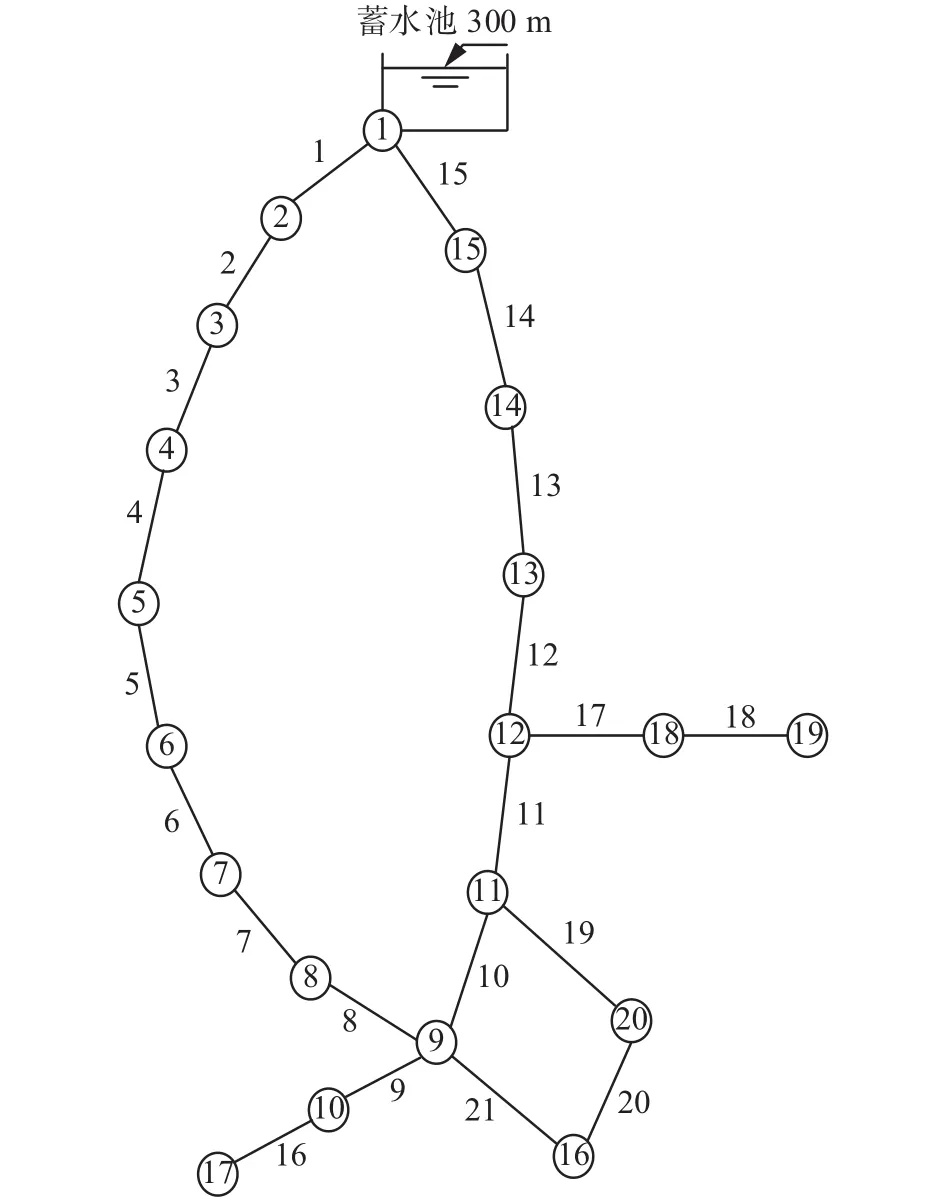
图 4 纽约管网Fig. 4 New York Tunnels network

1) IGD(inverted generational distance)[18]

IGD的定义如式(15)，其中P*为一组均匀分布在Pareto前沿上的解，P为算法所求得的非支配解，d(x, P)代表解x与P中解的最小欧式距离。如果P*中解的数量足够多，IGD在一定程度上能同时反映解的多样性和收敛性。IGD的值越小，算法所得解的多样性和收敛性越好。

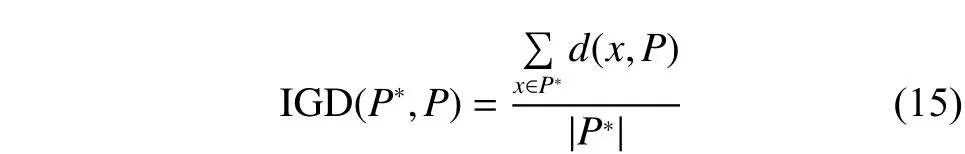
2) GD(generational distance)[19]

GD的定义如式(16)所示，其用于计算非支配解与Pareto前沿之间的距离。GD的值越小，算法所得解的收敛性越好。

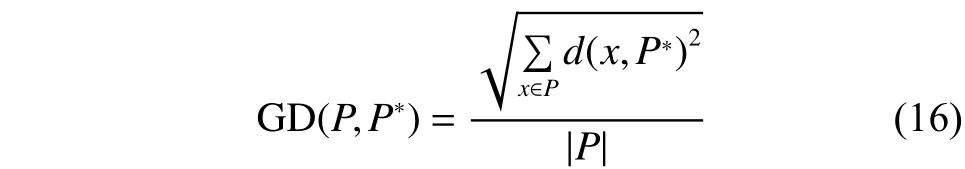
3) SP(spacing)[20]

SP用于计算非支配解中相邻解之间距离的方差，其公式如式(17)：

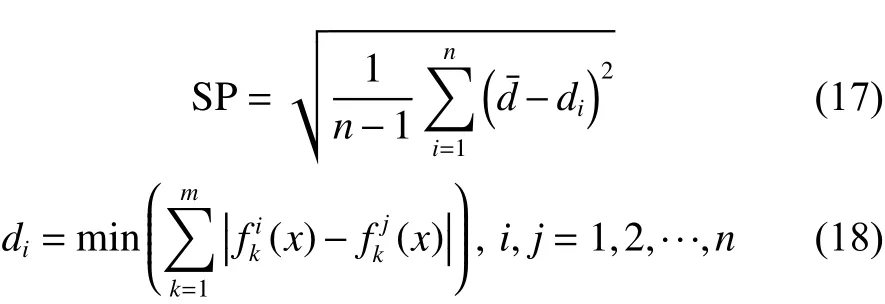
对于双环管网问题，RVSPEA2算法具体参数设置如表1所示，为了公平对比，SPEA2、NSGA-II和MOEA/D的参数设置与本文所提算法相同，每种算法均独立运行30次。表2列出了SPEA2、NSGA-II、MOEA/D与本文提出的RVSPEA2算法优化双环管网的结果。从表2中可以看出，在IGD、GD和SP 3个指标的均值上，本文提出的RVSPEA2算法都优于其他算法，说明在双环管网问题上，RVSPEA2算法所得解的多样性和收敛性最好。

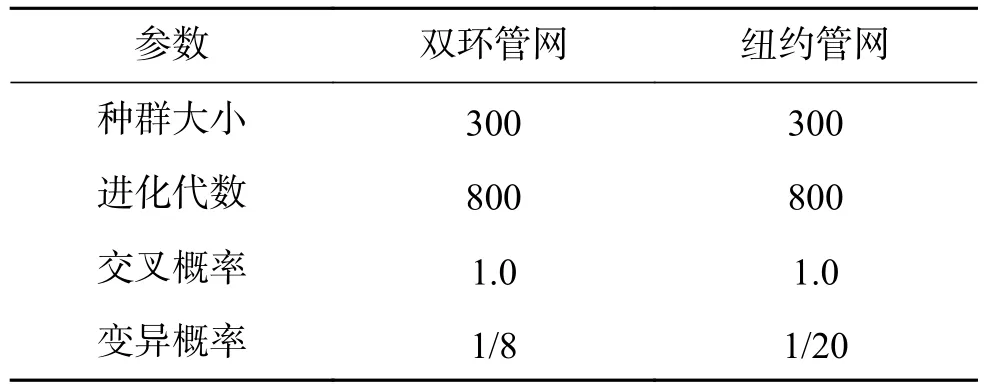
表 1 双环管网和纽约管网参数设置Table 1 Parameters of two-loop network and New York tunnels network

对于纽约管网问题，RVSPEA2算法具体参数设置如表1所示，SPEA2、NSGA-II和MOEA/D的参数设置与RVSPEA2算法相同，每种算法均独立运行30次。表3列出了SPEA2、NSGA-II、MOEA/D与本文提出的RVSPEA2算法优化纽约管网的结果。从表3中可以看出，本文提出的RVSPEA2算法在IGD、GD和SP这3个指标的均值上，都优于其他算法。因此，在纽约管网问题上，RVSPEA2算法所得解的多样性和收敛性也优于SPEA2、NSGAII和MOEA/D算法。

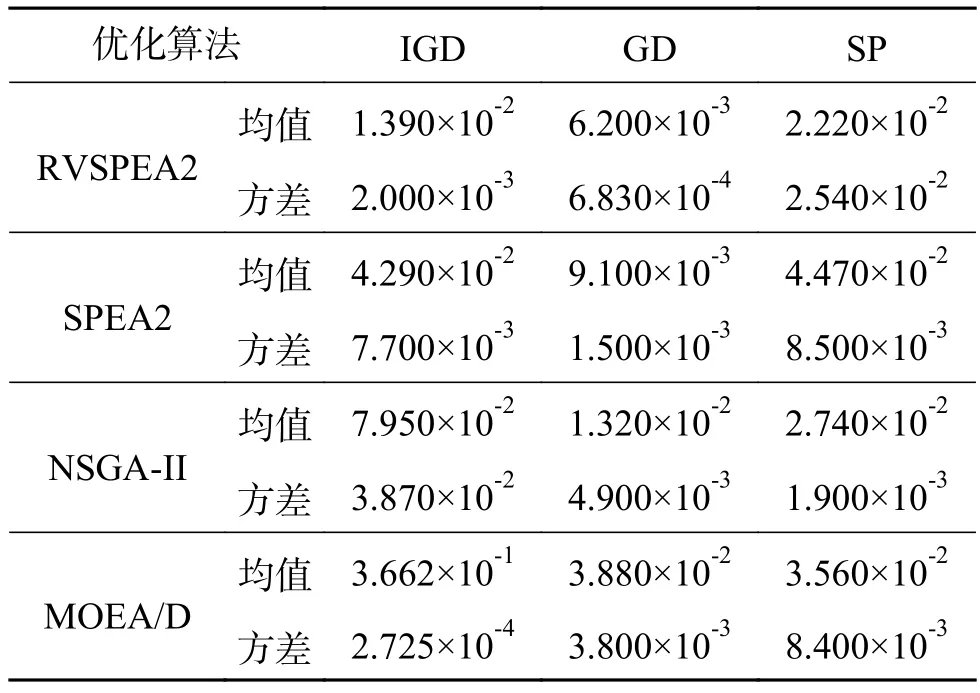
表 2 双环管网优化结果Table 2 Optimization results for two-loop network

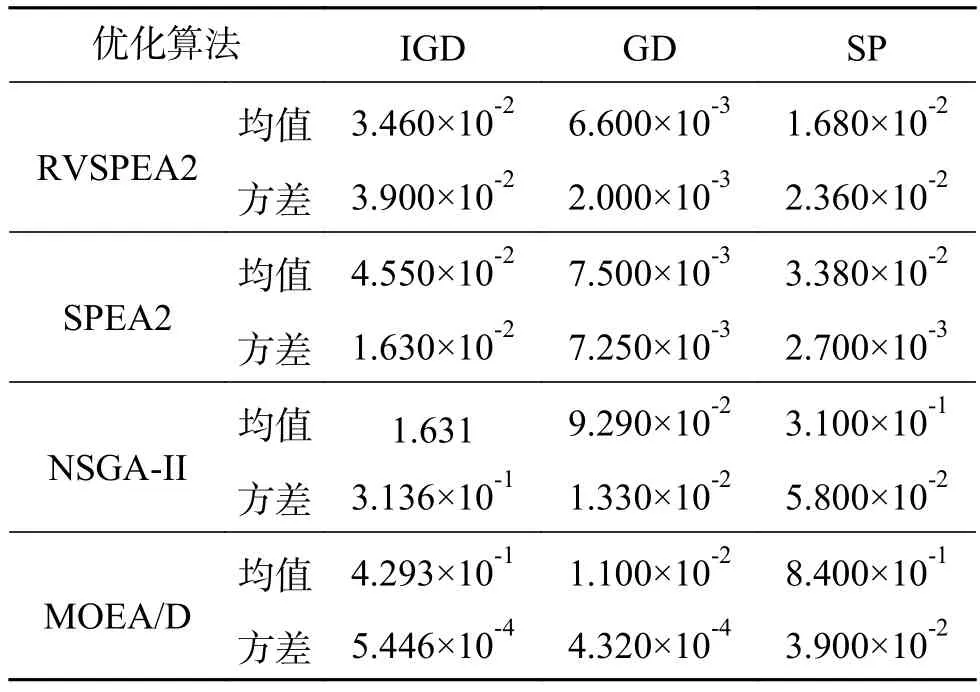
表 3 纽约管网优化结果Table 3 Optimization result for New York tunnels network

通过双环管网和纽约管网的测试，验证了本文提出的RVSPEA2算法在解决管网多目标优化设计上的性能。

3 工程实例

现将RVSPEA2算法应用于实际管网中。本实例为北京市某高校给水管网设计工程，管网布局如图5所示，管网中有1个水源、43个节点和60条管线。RVSPEA2算法参数设置如表4所示。图6画出了RVSPEA2算法所求出的非支配解。在实际工程应用中，应根据实际工程情况和决策者的经验，在保证供水基本可靠及居民正常用水的情况下，合理地选择一个施工方案。针对该实际工程问题，本文给出3个施工方案以供决策者选择，如表5所示。当资金有限时，应选择造价较低的方案，如方案A；当资金充足、管网可靠性更重要时，可采用节点富余水头总和小、节点富余水头方差小的方案，如方案C；当资金和管网可靠性同等重要时，可选择方案B。

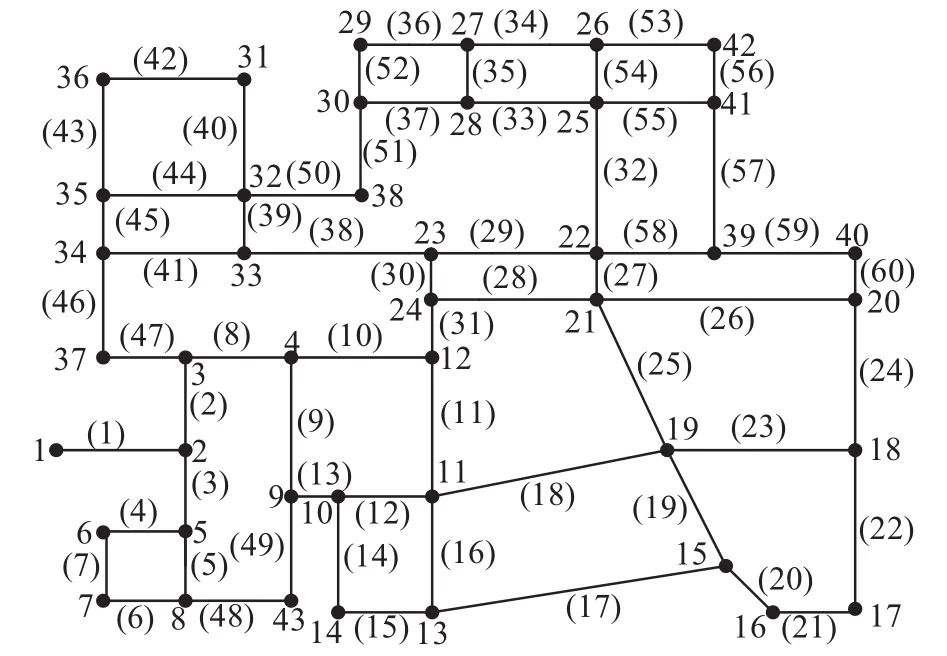
图 5 工程实例Fig. 5 Engineering example

表 4 工程实例参数设置Table 4 Parameters for engineering example

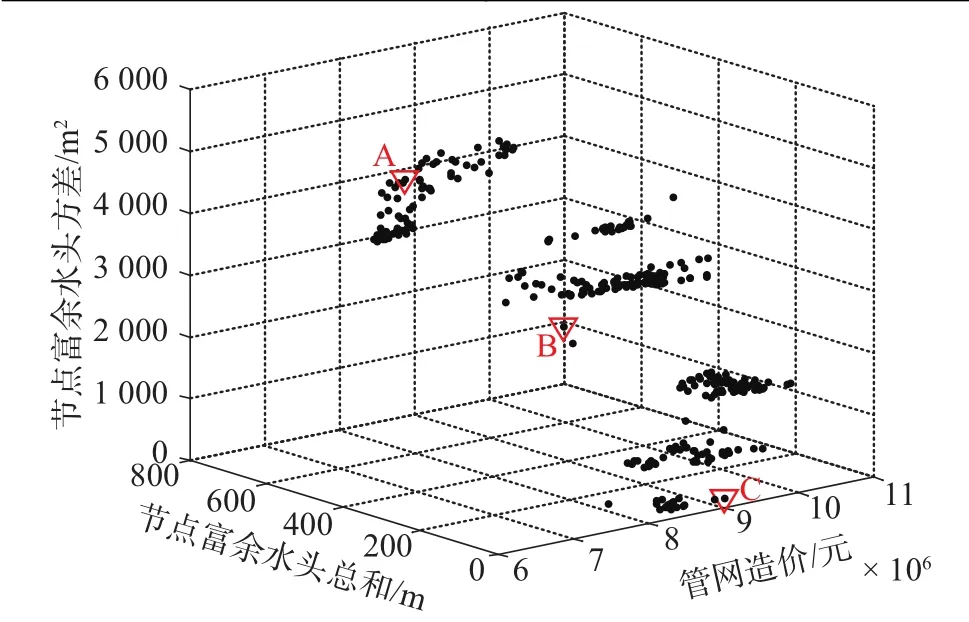
图 6 工程实例的非支配解Fig. 6 Non-dominated solutions for engineering example

表 5 3种不同情况下的施工方案Table 5 Construction schemes for three different cases

4 结束语

针对管网多目标优化问题，本文结合选择机制中支配和分解的思想，提出了一种基于参考向量的强度帕累托进化算法——RVSPEA2。该算法通过在目标空间中生成均匀分布的点，生成一组参考向量，并基于SPEA2算法的选择机制，将进化产生的解与各参考向量相关联，通过参考向量配合支配强度进行解的选择，提高了算法解的多样性和收敛性。两个经典管网的验证表明了RVSPEA2算法解决管网多目标优化问题的有效性。最后，本文将RVSPEA2算法应用于工程实例，并给出3种施工方案以供决策者选择。

[1]ALPEROVITS E, SHAMIR U. Design of optimal water distribution systems[J]. Water resources research, 1977, 13(6):885–900.

[2]MURPHY L J, SIMPSON A R, DANDY G C. Design of a pipe network using genetic algorithms[J]. Water-melbourne then artarmon, 1993, 20(4): 40–42.

[3]MORGAN D R, GOULTER I C. Optimal urban water distribution design[J]. Water resources research, 1985, 21(5):642–652.

[4]HALHAL D, WALTERS G A, OUAZAR D, et al. Water network rehabilitation with structured messy genetic algorithm[J]. Journal of water resources planning and management, 1997, 123(3): 137–146.

[5]MONTALVO I, IZQUIERDO J, SCHWARZE S, et al.Multi-objective particle swarm optimization applied to water distribution systems design: an approach with human interaction[J]. Mathematical and computer modelling, 2010,52(7/8): 1219–1227.

[6]LIU Haixing, YUAN Yixing, ZHAO Ming, et al. Hybrid multi-objective genetic algorithm for optimal design of water supply network[C]//Proceedings of the 12th Annual Conference on Water Distribution Systems Analysis. Tucson,United States, 2010: 899–908.

[7]刘书明, 李明明, 王欢欢, 等. 基于NSGA-II算法的给水管网多目标优化设计[J]. 中国给水排水, 2015, 31(5): 50–53.LIU Shuming, LI Mingming, WANG Huanhuan, et al.Multi-objective optimization design of water distribution system based on non-dominated sorting genetic algorithm-II[J]. China water and wastewater, 2015, 31(5): 50–53.

[8]蒋怀德. 给水管网多目标优化设计[D]. 上海：同济大学,2007, 5–7.JIANG Huaide. Multi-objective optimization design of urban water distribution networks[D]. Shanghai: Tongji University, 2007, 5–7.

[9]LI Mingming, LIU Shuming, ZHANG Ling, et al. Nondominated sorting genetic algorithms-iibased on multi-objective optimization model in the water distribution system[J].Procedia engineering, 2012, 37: 309–313.

[10]TOLSON B A, MAIER H R, SIMPSON A R, et al. Genetic algorithms for reliability-based optimization of water distribution systems[J]. Journal of water resources plan-ning and management, 2004, 130(1): 63–72.

[11]ZITZLER E, LAUMANNS M, THIELE L. SPEA2: improving the strength Pareto evolutionary algorithm: TIKReport 103[R]. Swiss: Swiss Federal Institute of Technology, 2001.

[12]DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE transactions on evolutionary computation, 2002, 6(2):182–197.

[13]ZHANG Qingfu, LI Hui. MOEA/D: a multiobjective evolutionary algorithm based on decomposition[J]. IEEE transactions on evolutionary computation, 2007, 11(6): 712–731.

[14]DEB K, JAIN H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: solving problems with box constraints[J]. IEEE transactions on evolutionary computation,2014, 18(4): 577–601.

[15]PRASAD T D, PARK N S. Multiobjective genetic algorithms for design of water distribution networks[J].Journal of water resources planning and management,2004, 130(1): 73–82.

[16]JIANG Siwei, CAI Zhihua, ZHANG Jie, et al. Multiobjective optimization by decomposition with Pareto-adaptive weight vectors[C]// International Conference on Natural Computation, Icnc 2011, Shanghai, China, 26–28 July.DBLP, 2011: 1260–1264.

[17]SEDKI A, OUAZAR D. Hybrid particle swarm optimization and differential evolution for optimal design of water distribution systems[J]. Advanced engineering informatics,2012, 26(3): 582–591.

[18]MA Xiaoliang, LIU Fang, QI Yutao, et al. A multiobjective evolutionary algorithm based on decision variable analyses for multiobjective optimization problems with largescale variables[J]. IEEE transactions on evolutionary computation, 2016, 20(2): 275–298.

[19]TANG Lixin, WANG Xianpeng. A hybrid multiobjective evolutionary algorithm for multiobjective optimization problems[J]. IEEE transactions on evolutionary computation, 2013, 17(1): 20–45.

[20]JIANG Shouyong, YANG Shengxing. Evolutionary dynamic multiobjective optimization: benchmarks and algorithm comparisons[J]. IEEE transactions on cybernetics,2017, 47(1): 198–211.