感应电机矢量控制系统的建模与仿真研究
李 松,陈 欢
感应电机矢量控制系统的建模与仿真研究
李 松,陈 欢
(武汉船用电力推进装置研究所,武汉 430064)
为了研究异步感应电机矢量控制系统动态性能,利用Matlab/Simulink建立了基于电压空间矢量脉宽调制( SVPWM)的感应电机矢量控制模型,并对电机的启动性能以及负载为阶跃输入情况进行了仿真分析。仿真结果表明所构建的系统模型动态过程符合实际调速系统运动过程。
感应电机 Matlab/Simulink 矢量控制 SVPWM
0 引言
交流电动机是多变量、非线性、强耦合的被控对象,20世纪70年代德国学者B laschke等人提出了矢量控制理论,使得交流感应电机定子电流励磁分量和转矩分量之间实现解耦,从而使交流异步电动机的磁通和转矩分别进行独立控制,这样交流异步电动机变频调速系统就具有了直流调速系统的全部优点。近年来电机控制中采用了SVPWM技术,也就是把电动机与逆变器看为一体,着眼于如何使电动机获得幅值恒定的圆形磁场为目标,它以三相对称正弦电压供电时交流电动机中的理想磁链为基准,用逆变器不同的开关模式所产生的磁链有效矢量来逼近基准圆,理论分析和实验表明,SVPWM调制具有脉动转矩小、噪音低,直流电压利用率高等优点[1,2]。本文在分析交流感应电机数学模型的基础上,建立SVPWM控制系统仿真模型,并验证感应电机在启动和不同负载情况下的性能。
1 矢量控制系统仿真模型
通过Matlab /Simulink[3]建立交流感应电机的控制系统仿真模型,主要有四个模块组成:交流感应电机模块、SVPWM控制模块、矢量控制模块和PI调节模块。如图1所示。
1.1交流感应电机模块
在实际应用中感应电机动态模型多采用坐标变换法建立,由于两相坐标轴互相垂直,两相绕组之间也没有磁的耦合,这样就可以将三相静止坐标系变为两相。
1.2转子磁链定向矢量控制模块
在三相坐标系下的定子输入电流通过坐标变换从三相静止坐标系到两相M -T轴旋转坐标系并且使得M轴沿转子总磁链矢量的方向最终等效成同步旋转坐标系下的直流电流i、i其中i用以控制转子磁链i用以调节电磁转矩。矢量控制的最终结果实现定子电流的分解对转子磁链和电磁转矩进行解耦控制则:


式中ωω—同步角速度,转子速度与转差角速度;—转子磁链的位置。根据方程组(1),在计算i、i时要将定子三相电流按照公式(2)进行坐标变换。
1.3 SVPWM控制模型
SVPWM模块如图2所示,图中将电压矢量分量u,u,开关周期Ts和直流端电压U作为输入。首先判断电压空间矢量扇区(N),接着计算中间变量( X,Y,Z),再由中间变量计算矢量作用时间(1,2),最后由扇区信号和其相应的作用时间,来确定电压空间矢量的作用次序和产生的PWM波形。
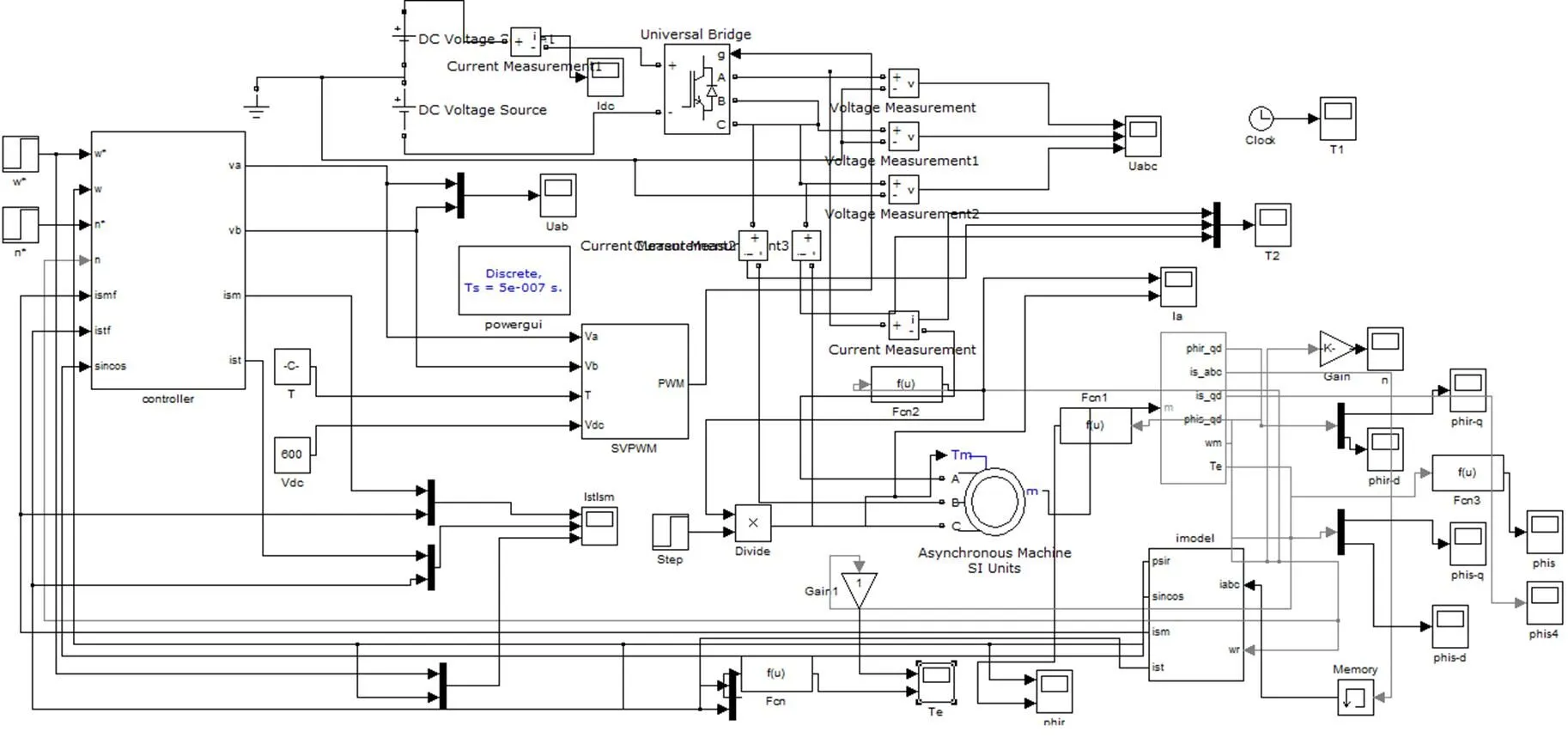
图1 感应电机矢量控制模块

图2 SVPWM模块
1.4调节器模块
该控制系统中总共有4个PI调节器,分别为转速调节器ASR、转矩电流调节器ACTR、磁链调节器AωR、励磁电流调节器ACMR,其控制框图如图3所示。
2 仿真结果与分析
为了验证所建模型的正确性,本研究采用如下电机参数进行仿真分析:额定功率为P= 4 kW,额定电压为380 V,频率为50 Hz,R= 0.435 Ω,R= 0.861 Ω,L= 0.071 H,L= 0.071 H,L= 0.069 H,P = 2,额定转速为= 1430 r/min,转动惯量= 0.19 kg/m2,直流侧电压为600 V,开关频率为5 kHz。

图3 调节器模块
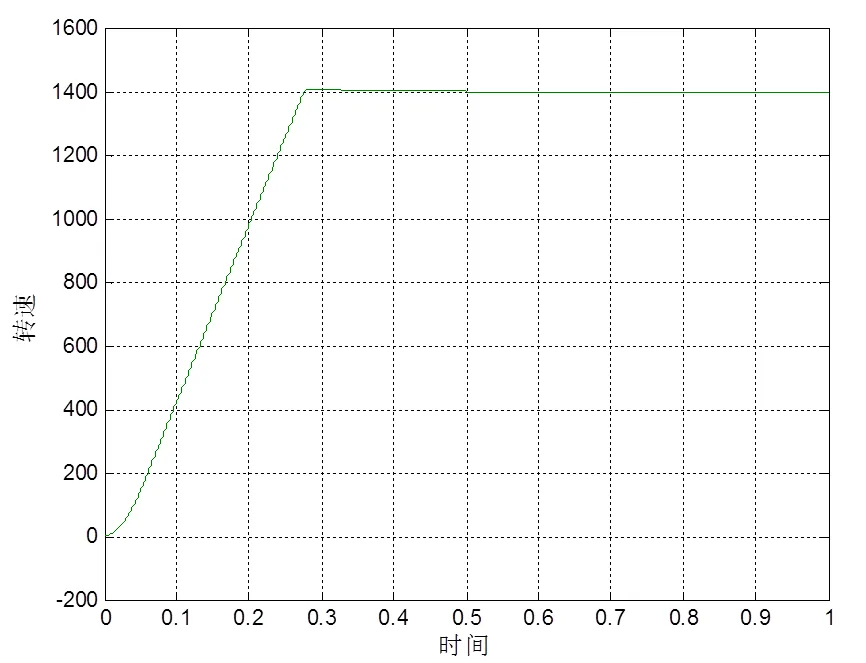
图4 转速响应曲线

图5 励磁电流响应曲线
转子磁通的给定值为0.96 Wb,负载初始值为空载,转速初始值为0,0 s 时突加转速给定1400 r/min,并且在0.5 s 时突加风机负载,其转速响应曲线如图10所示,从图中可以看出电机在小于0.3 s 的时间内转速便达到给定值,转速超调小于10 r/min;在0.5 s 突加负载时转速降落小于10 r/min,并在0.2 s 内恢复到给定值。
从图5、图6可以看出在电机启动时由于磁链尚未建立,磁链调节器处于饱和状态,输出最大励磁电流给定值,励磁电流调节器迅速跟踪励磁电流给定值,维持励磁电流为最大值,转子磁链迅速上升,约0.05 s 后磁链达到给定值,之后励磁电流迅速降低最后恒定,磁链响应非常迅速;从图7可以看出随着转子磁链幅值的上升,磁链的轨迹沿着螺旋线逐渐过渡到近乎圆形轨道。
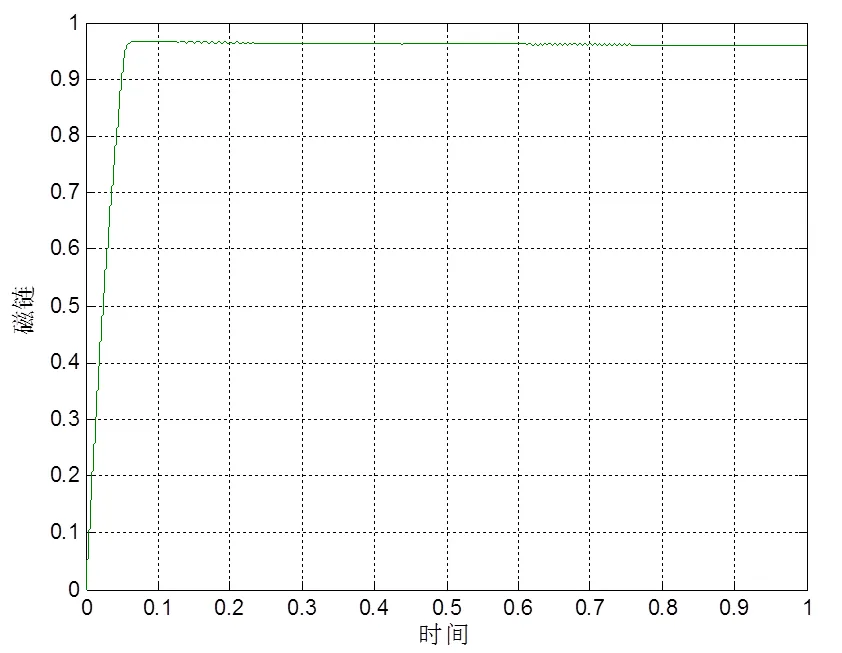
图6 磁链响应曲线

图7 转子磁链轨迹曲线
从图8可以看出在电机启动时由于转速尚未达到给定值,此时转速调节器处于饱和状态输出最大转矩电流给定值,转矩调节器迅速响应转矩电流给定值,使得电机转矩电流达到最大值,此时由于磁链早已建立,电机在最大电磁转矩作用下,转速迅速上升;在约0.27 s时转速达到给定值,此时在转速调节器和转矩电流调节器作用下,转矩电流迅速降低,电磁转矩也随之下降,下降到与负载转矩相等时,转速稳定在给定值;在0.5 s时电机突加负载,转速降低,在转速调节器作用下转矩电流迅速上升,电磁转矩随之上升,转速增加,最后稳定在给定值;从图9可以看出,在基频以下调速时,电机在转速0~1400 r/m之间可以保持转矩恒定,因此具有优良的动态性能。图10给出了定子三相电流,从图中可以看出,电机定子电流均为正弦波形,且在在启动及加载时电流会随之变大,但均在电机过载范围之内。
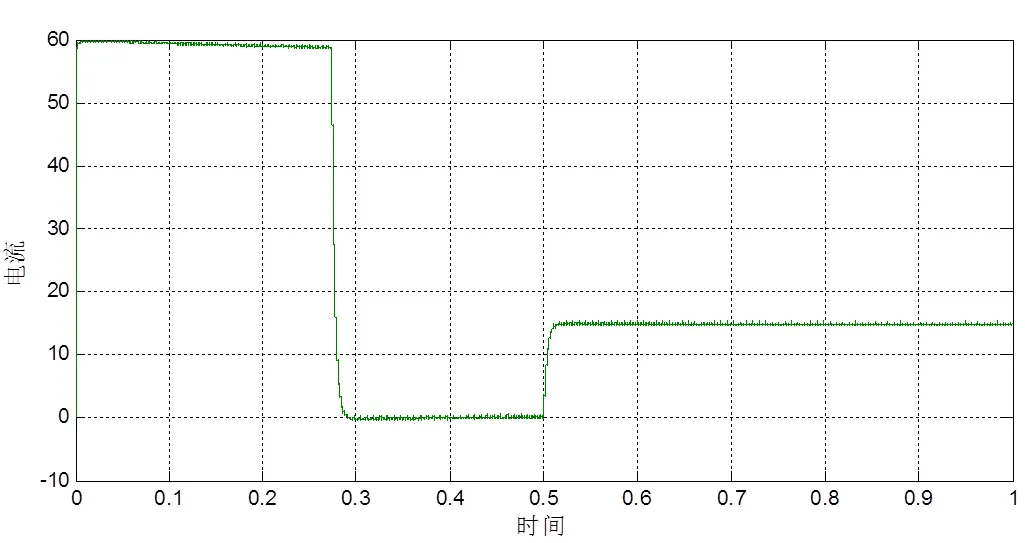
图8转矩电流响应曲线
3 结论
当空载调速时,启动电流,转矩和调速性能满足假设要求。当负载转矩为20 N·m 的阶跃信号时,转矩的波动量为100%,超调量仅为1.5%。从结果可以看出,动态仿真过程符合实际调速系统运动过程。

图10定子电流曲线
[1] 陈伯时. 电力拖动自动控制系统[M]. 第三版. 北京:机械工业出版社, 2004.
[2] 李永东. 交流电机数字控制系统[M]. 北京: 机械工业出版社, 2002.
[3] ALKORTA P, BARAMBONES O, GARR IDO A J , et al.SVPWM variable structure control of induction motor drives[J]. IEEE Tran s. Industr ia l Electron ics, 2007, 40 (7): 1195 - 1200.
[4] 黄忠霖, 周向明. 控制系统Matlab计算及仿真实训[M ]. 北京: 国防工业出版社, 2006.
[5] 王晓明, 王玲. 电动机的DSP控制: TI公司DSP应用[M ]. 北京: 北京航空航天大学出版社, 2004.
[6] RAMANA M V, RAO B, MANGU K. Sashi Kanth. Spacevector pulse widthmodulation control of induction motor[J]. IET2UK In ternational Conference on Information and Communication Technology in Electrical Sciences, 2007, 12 (20): 349 - 354.
Modeling and Simulation of Induction Motor Vector Control System
Li Song, Chen Huan
(Wuhan Institute of Marine Electric Propulsion, Wuhan 430064, China)
TP391.9
A
1003-4862(2018)02-0018-04
2017-11-27
李松(1985-),男,硕士,工程师。研究方向:电力电子控制及自动化控制。Email: 584227374@qq.com

