基于KSVD学习字典稀疏表示的图像压缩传感方法研究
王 宇,欧阳华
基于KSVD学习字典稀疏表示的图像压缩传感方法研究
王 宇,欧阳华
(海军工程大学电气工程学院,武汉 430033)
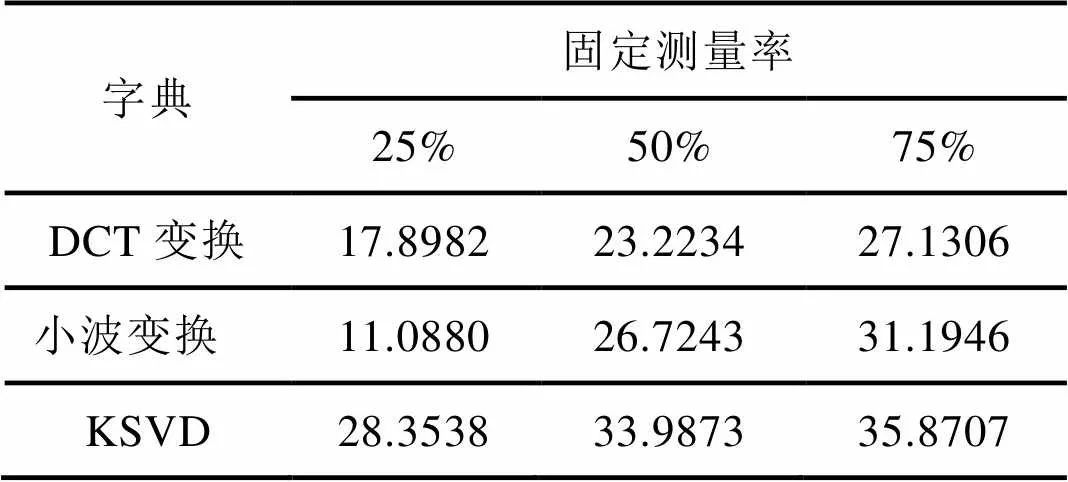
本文运用基于KSVD学习字典的稀疏表示方法,实现了图像信号的压缩传感。将实验结果与DCT变换和小波变换固定字典进行对比分析,分别采用25%、50%、75%三种测量率,三种测量率下的峰值信噪比(PSNR)明显高于相同测量率下的DCT变换与小波变换的峰值信噪比。尤其是在测量率为25%时,DCT变换与小波变换的PSNR分别为17.8982与11.0880,而KSVD学习字典的PSNR为28.3538。实验结果表明采用KSVD方法在图像压缩传感上有更好的实验效果。
压缩传感 小波变换 DCT变换 KSVD
0 引言1
传统的信号采集过程主要包括采样、压缩、传输和解压四个部分。但在这个过程中,依照Nyquist-Shannon定理抽样频率至少要是原信号最高频率的两倍以上才能由抽样后的离散信号精确地恢复出原信号这一标准,将会产生大量的冗余数据,大大增加了处理数据的时间和存储数据占用的存储空间[1]。2006年,Candes和Donoho提出压缩传感理论(Compressed Sensing, CS)[2-3],该理论认为稀疏的或具有稀疏表达的有限维数的信号可以利用远少于奈奎斯特采样数量的线性、非自适应的测量值无失真地重建出来。其核心思想是:若信号在某个变换域上具有稀疏性,可将其线性投影到一个低维空间中实现信号压缩,此过程可将信号的采样以及压缩过程合二为一。信号的重构可通过求解线性优化问题实现。压缩传感技术能够通过观测直接获得压缩的信号,避免对大量信息的采集。压缩传感技术在图像采集、图像压缩和医学成像等领域具有广阔的应用前景[4]。由于压缩传感理论使采集很少一部分数据并且运用这些少量数据重构出更大量的数据,开拓了在信息处理方面的新思路。随着理论的渐渐成熟,压缩传感技术的应用成为人们的研究热点。从雷达成像到医学成像,压缩传感技术在图像上的应用越来越多,越来越深入[5,6]。
本文研究了基于KSVD学习字典稀疏表示的图像信号压缩传感和重构,并与DCT变换固定字典和小波变换固定字典进行了对比分析。
1 压缩传感理论
1.1压缩传感理论简介

一般来讲,信号本身不是稀疏的,但是在一个合适的变换域下变换得到的系数是可以被认为是稀疏的。例如,对信号x进行小波变换,保留K个得到的最大的系数,并将其他的N-K个系数设为零,而这N-K个系数对信号的重构没有太大的作用,随后通过相应的反变换来重构信号。在这里,信号x可以被认为是在小波基下K稀疏的。

通过结合(1)与(2)可以得到:
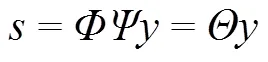
如上所述,通过CS可以把一个N维信号降到M维。在(2)中,由于N>M,所以直接解决(2)是无法重构信号x的。然而在(3)中,由于y是K稀疏的,即只包含K个非零系数,且K 解决的算法最常用的有MP、OMP、CP、GP等。 稀疏表示问题的基本问题是字典的选择[7]。多数求解方法都可以根据两种不同的字典构造方式分成两类:基于分解的方法和基于机器学习构造字典的方法[8]。在基于分解的方法中,需要为数据预先定义数学函数模型。这些字典包括:傅里叶变换、离散余弦变换和小波变换等。通过这种方法构造的字典通常具有高度结构性和快速算法,但是也有相应的一些局限。离散余弦变换可以较好实现一维信号的压缩传感重构[9]。小波变换基能很好的捕捉图像的点状奇异,因而基于小波变换实现图像的压缩传感重构。但这两种方法都是只有针对某种特定的信号才会有较好的重构精度,普适性较差。第二种方法则是通过大量的训练实例推导出字典。字典学习算法包括:最大似然方法ML、MOD[11]和KSVD[12]等。这种字典的好处体现于精度和普适性,但同时也消耗更多的运算时间和运算资源。 压缩感知主要由信号的稀疏表示、测量矩阵的设计和信号重构算法三个部分构成。本文主要研究信号的稀疏表示这一部分内容。 为了更精炼地表达一个信号,通常可以把信号变换到一个新的基或框架下,当非零系数的个数远少于原始信号的长度时,可以把这些少量的非零系数称为原始信号的稀疏性表达。 信号的稀疏化是压缩传感应用的理论基础,通用的稀疏方法有快速傅里叶变换(FFT)、离散小波变换(DWT)、离散余弦变换(DCT)等。三种稀疏方法各有各的优缺点,本文就对比分析了DCT、 DWT与KSVD三种方法在图像的压缩传感应用中实际效果的优劣性。 KSVD算法的优化之处是会对字典进行逐列更新,从而提高精度。 1)稀疏表示 2)字典更新 两人来到一家咖啡店,坐到桌旁。侍者端来两杯咖啡,苏婷婷问:张阳,有什么话你说吧!张阳想了想:婷婷,离开杰克吧,你和他不合适。苏婷婷不服地:你怎么知道我和杰克不合适?张阳自信地:我能感觉出来,婷婷,我爱你。苏婷婷站起身:张阳,还有别的话吗?没有我走了!张阳无奈地:好,我不说这个了。苏婷婷刚要坐下,看见杰克和一个外国朋友走进来,二人目光相遇,杰克看看张阳…… KSVD算法通过构建字典来对数据进行稀疏表示,并且不断迭代更新。KSVD算法分为两步,即稀疏表示与字典更新。 KSVD算法: 1)初始化。k=0;构造(0)R,可以使用随机元素,也可以使用m个随机选择的样本;将(0)的各列归一化。 2)主迭代。k增1,并执行以下步骤: ①稀疏编码阶段:使用追踪算法近似求解,即 为了对比分析DCT字典、小波变换字典和KSVD字典在压缩传感应用中的实际效果,本文进行了下面几组仿真实验。首先,实验中使用测试图像lena,采用不同的稀疏变换字典,分别对测试图像进行压缩传感测试,测量率为50%,如图1、图2、图3和图4所示。 图1 lena原始图像 图2 DCT变换字典 通过图2、图3与图4的对比,我们明显可以看出小波变换字典在图像压缩传感中的实际应用效果明显优于DCT变换字典,而KSVD字典明显优于前两种字典。 图3 小波变换字典 图4 KSVD字典 再分别采用不同的采样率和稀疏变换字典,对图像进行压缩传感,比较峰值信噪比(PSNR),如表1所示。 表1 不同测量率和字典下恢复图像的PSNR值 PSNR数学表达式为: 其中,MSE是原图像与恢复图像之间的均方差。 根据表1数据,我们可以看出在三种测量率下,KSVD字典在压缩传感中的实际效果都要高于DCT字典和小波变换字典。尤其当测量率为25%时,采样率过低,从而导致DCT与小波变换两种方法的实际重构效果都不是很好,但此时KSVD字典仍然可以较好的重构出原图像。 本文对图像压缩传感的稀疏变换方法进行了研究,分别采用DCT、小波变换与KSVD算法三种方式和不同的测量率,对图像lena进行稀疏变换。最后通过压缩传感后的图像恢复效果对实验结果进行对比分析。仿真实验表明了,在图像的压缩传感中,KSVD的实际应用效果明显好于DCT变换与小波变换,PSNR值更高。测量率越高信号的重构效果越好。 [1] 李树涛, 魏丹. 压缩传感综述[J]. 自动化学报, 2009, 35(11): 1369-1377. [2] Donoho D.Compressed sensing[J]. IEEE Trans on Information Theory, 2006, 52(4): 1289-1306. [3] Candes E. Compressive sampling[C]. Proceedings of International Congress of Mathmaticians. Madrid,Spain: European Mathematical Society Publishing House, 2006: 1433-1452. [4] J.Haupt and R.Nowak. Compressive Sampling Vs Conventional Imaging [C]. 2006 IEEE International Conference on Image Processing, 2006:1269-1272. [5] 石光明, 刘丹华, 高大化, 等. 压缩感知理论及其研究进展[J]. 电子学报, 2009, 37(5): 1070-1081. [6] 高敏. 基于CS的SAR目标识别[D]. 西安电子科技大学硕士学位论文, 2010. [7] R. Rubinstein, A. Bruckstein, and M. Elad. Dictionaries for sparse representation modeling. Proc. IEEE Special Iss. Applicat. Sparse Represent. Compress. Sens., 2010, 98(6): 1045-1057. [8] 邓承志. 图像稀疏表示理论及其应用研究[D]. 华中科技大学博士学位论文, 2008. [9] Y. Tsaig and Carin L. Exploiting structure in wavelet-based Bayesian compressive sensing[J]. IEEE Trans. Signal Processing, 2009, 57(9): 3488-3497. [10] K.Engan, S. Aase, and J. Hakon-Husoy. Method of optimal directions for frame design[C]. In Proc. IEEE Int. Conf. Acoust., Speech, Signal Process., 1999, 5: 2443-2446. [11] Aharon M, Elad M, Bruckstein A M. K-SVD: An algorithm for designing of vercomplete dictionaries for sparse representation[J]. IEEE Trans. on Signal Processing, 2006, 54(11): 4311-4322. Research on Image Compressed Sensing Method Based on KSVD Learning Dictionary Sparse Representation Wang Yu, Ouyang Hua (College of Electrical Engineering, Naval University of Engineering, Wuhan 430033, China) TN915 A 1003-4862(2018)02-0037-04 2017-11-17 青年科学基金(No.51307178) 王宇(1993-),男,硕士。研究方向:信号检测与处理。Email:840724234@qq.com
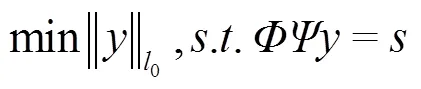
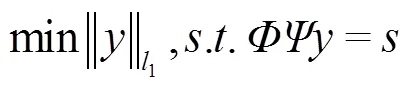
1.2压缩传感理论的稀疏表示
2 KSVD方法
2.1 KSVD算法原理

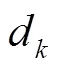

2.2 KSVD字典构造
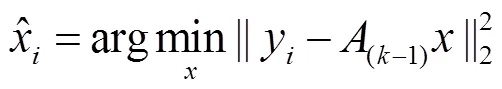
3 仿真实验





4 结论

