复变量表示土体参数随机性的边坡稳定分析

宋会彬，朱月建

(1.中国恩菲工程技术有限公司，北京 100038； 2.江西铜业集团银山矿业有限公司，江西 上饶 334201)

1 前言

边坡的稳定性分析是岩土工程中重要的研究课题之一[1]，也是边坡工程的一个研究热点。边坡的变形、失稳，从根本上说是自身获得稳定状态的重新调整过程，而协助边坡趋于稳定的作用因素有自然因素和人类活动的因素[2]。目前，边坡稳定分析主要分为确定性分析和不确定性分析两大类[3]。确定性分析方法就是将影响边坡稳定的各因素作为确定量来考虑的，安全系数通常作为其计算的基础。边坡稳定性分析及判断边坡是否稳定的最基本方法是确定性分析方法，其主要分为以下几种[3]：极限平衡法(LEM)、离散单元法(DEM)、边界单元法(BEM)、有限单元法(FEM)、不连续变形分析方法(DDA)、界面元法(ISEM)以及快速拉格朗日法等。大约在20世纪70年代初，由于可靠度、人工智能等一些新理论和方法的出现以及大量不确定因素在边坡工程设计和分析中越来越被人们重视，边坡稳定分析中的不确定性分析方法开始出现。导致边坡稳定分析结果具有不确定性的主要因素有：①计算模型和计算方法的局限性，例如应用各种条分法时需要的一些假设；②计算模型中岩土体土性参数的不确定性。在各种不确定性因素中土性参数的不确定性是影响边坡稳定分析的关键因素，目前主要的不确定性方法包括可靠度方法、模糊数学法、人工智能法和灰色预测系统法等几种[3]。

由于不确定性是土体参数固有的性质，因此在进行边坡稳定性分析时土体参数的不确定性应予以考虑。目前，实际工程中对边坡的稳定性分析仍然采用确定性的安全系数法，同时通过选取“足够高”的允许安全系数来弥补各种未能考虑的不确定性，并以此作为边坡安全性的判断依据。允许安全系数的选取国内外有所不同，例如英国及加拿大的允许安全系数为[Fs]=1.3，美国[Fs]=1.2～1.3，在我国绝大多数边坡的允许安全系数取为[Fs]=1.1～1.3[4]。选取允许安全系数的方法能够在一定程度上考虑由于数据的离散性及计算方法不确定性给计算结果带来的风险，但是允许安全系数基本上是依据工程师的经验来判断确定的，具有一定的主观性[4]。并且不同工程选取相同的安全系数，不利于分析不同因素产生的不确定性对边坡稳定性的影响，各种不确定性因素之间不容易比较、分析和判断。因此，将土体参数本身的不确定性考虑到边坡稳定性分析中是十分必要的。随着认识的不断深入，数学中的概率理论已被大量应用于土体参数的不确定性描述中。此种方法将土体的渗透系数、容重、粘聚力、内摩擦角等参数当作随机变量进行研究。在实际工程中，由于各方面条件的限制，得到的土体参数数据往往十分有限，很难得到不确定性参数完整的概率分布情况。本文基于以上难点，以复变量形式表示土体各参数，将参数的不确定性用变异值表示，应用各种极限平衡法求得安全系数及其变异范围，进而进行边坡稳定性分析。此计算方法既利用了已有的有限的客观土体参数数据，又加入了由工程经验得到的主观判断因素，应用更加灵活、可靠。

2 复变量表示土体参数随机性的边坡稳定分析理论基础

极限平衡条分法是目前边坡稳定性分析中应用最为广泛的方法，此方法是建立在莫尔—库仑强度准则的基础上，其特点是只考虑静力平衡条件和莫尔—库仑破坏准则。尽管极限平衡条分法没有考虑岩土的应力—应变关系，但由于其概念清晰，计算方法简单，故该方法仍是实际工程边坡稳定性分析的主要方法。

2.1 复变量表示土体参数随机性的极限平衡法

极限平衡条分法由于其概念清晰，计算方法简单，在工程中得到广泛应用。但由于本身的局限性及影响边坡稳定的各因素的不确定性，使得有些边坡稳定计算即使得到的安全系数较高，仍是发生了破坏，因此在边坡稳定性分析中考虑边坡土体参数的不确定性是十分必要的。

在应用极限平衡条分法进行边坡稳定性分析时，土体不确定性计算参数主要包括容重、粘聚力和内摩擦角等。这些参数的随机性，在大量的取样和试验基础上可以应用数理统计方法获得其概率分布形式、均值和方差。但在实际工程中，土体参数的资料整理和试验统计往往会受到以下因素的制约。

(1)土工试验组数少。由于实际情况限制，关于抗剪强度、渗透系数等的试验组数通常不多，导致数理统计时样本数量太少，很难满足统计要求。

(2)复杂土工试验本身存在误差。一些复杂的土工试验在试验本身设计上就已经包含一定的误差，因此，这些试验成果不能很好地反映实际情况。

因此，当试验数据非常有限时，可根据工程经验或土体参数的统计资料进行估算。本文采用与复变量表示渗透系数法相同的原理，将土体参数容重，有效粘聚力和有效内摩擦角用复变量形式表示，具体表示形式如下：

(1)

(2)

(3)

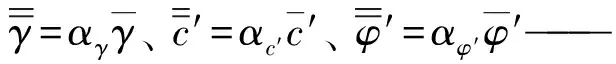
αγ、αc′、αφ′——分别为土体容重、有效粘聚力和有效内摩擦角的变异系数。

应用以上考虑随机性的的土体参数，对传统的瑞典条分法和简化Bishop条分法进行改进。

2.2 改进瑞典条分法

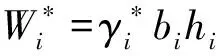
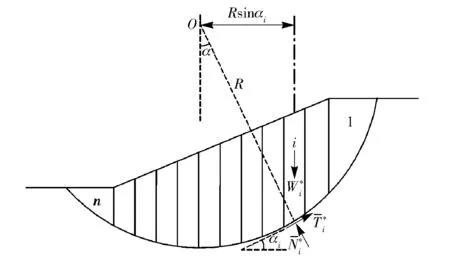
图1 改进瑞典条分法受力分析示意图

根据土条i的静力平衡条件有：

(4)

式中：αi——该土条底面中点的法线与竖直线的交角。

(5)

将整个滑动土体中各土条上的作用力对滑弧圆心O取力矩平衡得：

(6)

将式(4)代入式(5)后，再将式(5)代入式(6)可得到改进瑞典条分法的计算公式如下：

(7)

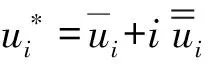
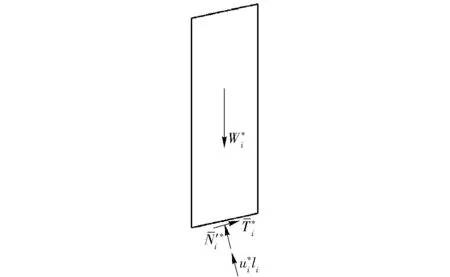
图2 土条i上有孔隙水压力时受力分析示意图

改进瑞典条分法的计算公式可改用有效应力来表达，具体形式如下：

(8)

式中：c′i*、φ′i*——为土条i底面土层的有效粘聚力和有效内摩擦角。

传统瑞典条分法[6]是最初的也是最简单的条分方法，由于该方法忽略了条间力的作用，无法满足所有的静力平衡条件，因此应用此方法计算出的安全系数一般比其他严格的方法计算的安全系数低10%～20%，在滑弧圆心角较大，并且孔隙水压力较大时，计算的安全系数可能比其他较严格的方法小一半。

2.3 改进简化Bishop条分法

传统的Bishop条分法[6]也是假定滑动面为滑弧面，它考虑了土条侧面的作用力，并假定各土条底部滑动面上的抗滑安全系数均相同，即等于滑动面的平均安全系数。Bishop采用了有效应力方法推导公式，该法也可用总应力分析。

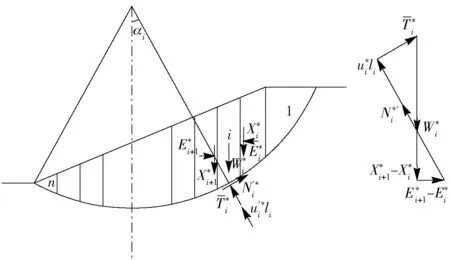
图3 改进Bishop条分法受力分析示意图

(9)

取土条i竖直方向力的平衡有：

(10)

将式(9)代入式(10)得：

(11)

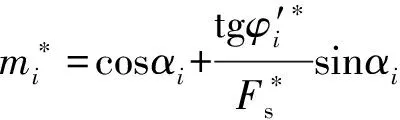
(12)

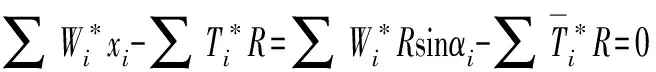
(13)

将式(11)代入式(9)后，再代入上式，得：

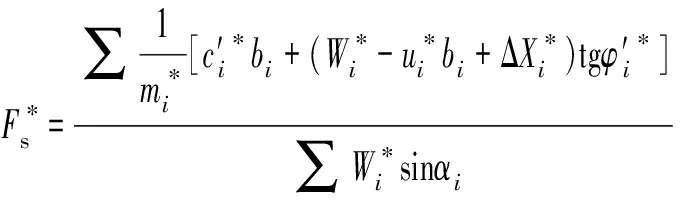
(14)

(15)

本文在应用改进瑞典条分法和改进简化Bishop条分法计算的安全系数时，采用式(8)和式(15)形式，即选用有效应力计算。安全系数的复变量表示形式如下：

(16)

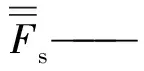
(17)

式中：F′s——折减后的最小安全系数，表示在考虑参数随机性的情况下，最小安全系数变化后的数值。本文算例中，应用F′s来重新判断边坡的稳定性。

危险滑弧的确定及其对应的最小安全系数是边坡稳定性分析中最为关键的问题之一。瑞典条分法和简化Bishop条分法的滑裂面形式均为圆弧，而圆弧的确定需要有3个量，即圆心的x、y坐标和圆的半径。工程中常用的搜索最危险滑动面的方法有限元法中的二分法[7]、坐标轮换法[8]、0.618优选法[9]、遗传算法[10]等。本文采用与殷宗泽等编制的SLP程序相同的0.618优选法确定危险滑弧面的位置。

3 数值算例

由于地质构造运动、沉积等原因，造成土坡坡体材料一般不会是均质的，且各材料的分层也不一定具有规律性，如倾斜、折线等形式。为了使数值算例更具有普遍性，本文选用水平分层边坡和斜折线分层边坡作为典型算例，应用复变量表示土体参数的改进瑞典条分法和改进简化Bishop条分法进行边坡稳定性分析，并将计算结果与SLP程序的瑞典条分法、简化Bishop条分法等进行比较。

3.1 水平分层边坡

参见文献[11]中算例19，水平分层边坡如图4所示。坡高H=60m，坡比为1∶2，各土层介质土性参数参考文献[11]获得，容重、有效粘聚力和有效内摩擦角的变异系数选用见表1。

图4 水平分层边坡剖面图

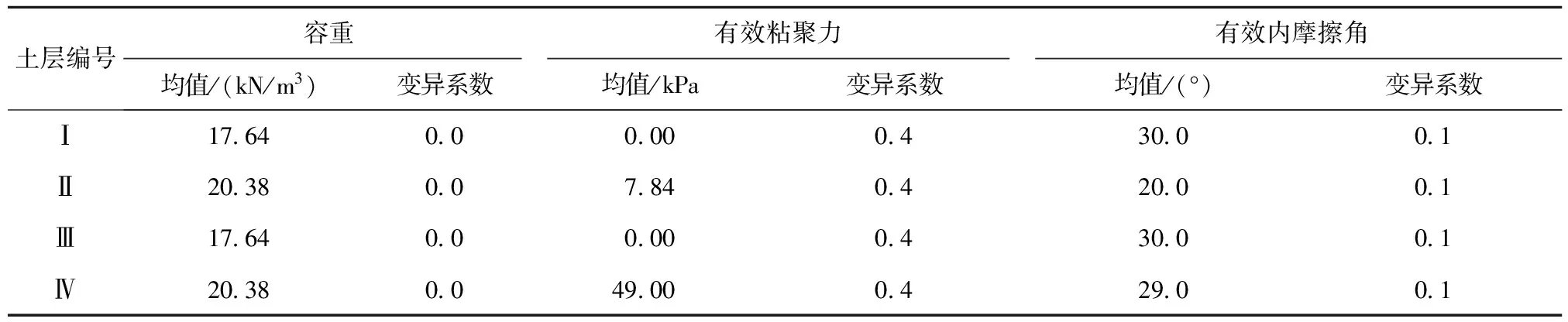
表1 水平分层边坡土体物理力学参数

各种方法计算的最小安全系数及安全系数变异值如表2所示。

由表2可看出此水平分层边坡模型利用改进瑞典条分法和改进简化Bishop条分法计算的最小安全系数比瑞典条分法和简化Bishop条分法的计算结果稍小，折减后的最小安全系数仍在安全范围之内。另外，研究结果表明，各方法计算的危险滑弧面的位置颇为接近。

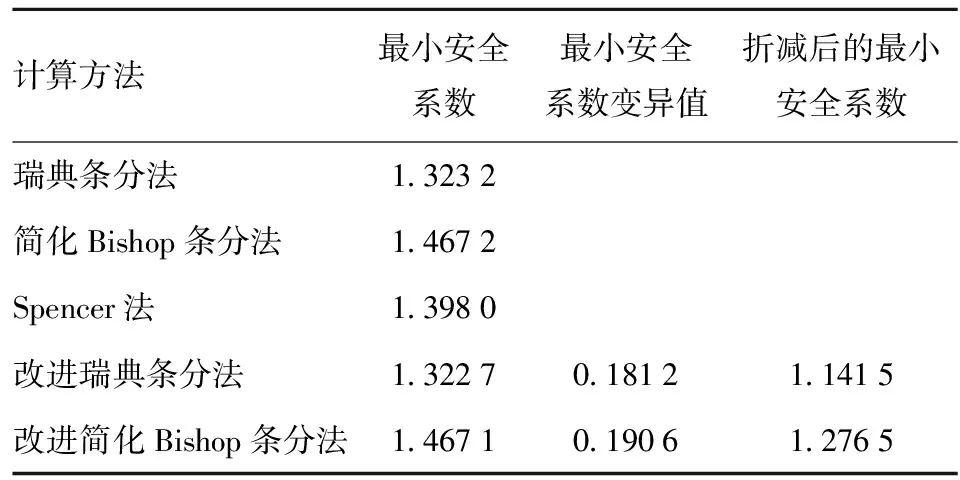
表2 水平分层边坡最小安全系数对比

3.2 斜折线分层边坡

参见文献[11]中算例3，斜折线分层边坡如图5所示。坡高H=10m，坡比为1∶2，各土层介质土性参数参考文献[11]获得，容重、有效粘聚力和有效内摩擦角的变异系数选用见表3。

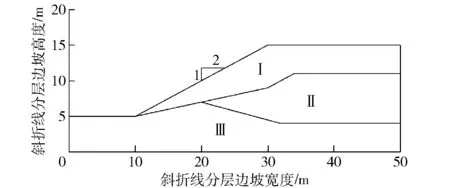
图5 斜折线分层边坡剖面图

表3 斜折线分层边坡土体物理力学参数

各种方法计算的最小安全系数及安全系数变异值如表4所示。

表4 斜折线分层边坡最小安全系数对比

由表4可看出此斜折线边坡模型利用改进瑞典条分法和改进简化Bishop条分法计算的最小安全系数与瑞典条分法和简化Bishop条分法的计算结果基本一样，但改进瑞典条分法折减后的最小安全系数为1.046 7，低于国内的安全系数1.1～1.3的标准，则此边坡稳定分析的结果由安全变成了不安全。各方法计算的危险滑弧面的位置颇为接近。在工程设计施工中，计算分析和实际施工是相互影响的，因此应用改进瑞典条分法及改进简化Bishop条分法进行边坡稳定计算，不仅可以分析边坡的稳定性，还可进一步指导工程施工，提高施工质量。

4 结论

(1)通过比较典型分层边坡在各种算法下的稳定性计算结果，得出复变量表示土体参数的改进瑞典条分法和改进简化Bishop条分法计算的最小安全系数与瑞典条分法和简化Bishop条分法的计算结果较接近，危险滑弧面的位置也基本相同。

(2) 复变量表示土体参数的改进瑞典条分法和改进简化Bishop条分法在边坡稳定计算中，除可得到最小安全系数的确定值，同时可以获得最小安全系数的变异值。最小安全系数变异值可以在一定程度上反映最小安全系数的波动范围，体现了土体参数不确定性对安全系数计算的影响。在计算中发现一些边坡稳定问题，当进行确定性分析时，得到的安全系数在国家允许安全系数的取值范围内。但若考虑到土体参数的变异性，综合考虑计算得到的安全系数及其变异值，可发现最小安全系数有可能不在允许安全系数的取值范围内，则此边坡稳定分析的结果由安全变成了不安全。由于工程设计施工中计算分析和实际施工的相互影响，因此最小安全系数的变异值不仅可以用于分析边坡的稳定性，还会进一步影响到工程施工。

[1] 陈祖煜.土质边坡稳定分析[M].北京：中国水利水电出版社,2003.

[2] 崔政权,李 宁.边坡工程——理论与实践最新发展[M].北京:中国水利水电出版社，1999.

[3] 莫素华.边坡稳定性研究方法[J].中国水运(学术版),2007，(2)：101-104.

[4] 谢桂华.岩土参数随机性分析与边坡稳定可靠度研究[D].长沙:中南大学,2009.

[5] 杨召亮.基于潘氏极值原理的边坡稳定性的整体分析法[D].宜昌:三峡大学,2010.

[6] 卢廷浩.土力学[M].南京：河海大学出版社,2002.

[7] 江见鲸，等.土建工程常用微机程序汇编[M].北京:水利电力出版社,1987.

[8] 包承纲，等(译).Yang H H.土坡稳定分析[M].北京:清华大学出版社,1988.

[9] 殷宗泽,郭志平,徐鸿江，等.条分法土坡稳定分析计算程序(SLP) [A].姜宏道,赵光恒,向大润等编.水工结构工程与岩土工程的现代计算方法及程序[C].南京:河海大学出版社,1992.343-351.

[10] 肖专文,张奇志,梁 力,等.遗传进化算法在边坡稳定性分析中的应用[J].岩土工程学报,1998,20(1):44-46.

[11] Rocscience I.Slide Verification manual[R].Toronto:Rocscience Inc.,2003.8-118.