连续体采摘机械臂末端静态承载姿态等效模型建立与验证

王 皓，高国华，夏齐霄，李炼石，任 晗

0 引 言

近年，随着农业设备自动化程度的提升，农业自动化装备机器人的性能指标逐年提高。特殊作业环境及作业对象的复杂性对机器人在与环境的协调能力、自适应能力及灵活性等方面都提出了较高的要求。连续体机械臂因其柔性、自适应性及灵活性的特征逐渐进入研究者的视野中。相比于传统机械臂，由柔性部件构成的连续体机械臂在采摘等作业中，由于自身在外力下可柔性变形，不会伤及枝叶和果蔬，使得它在农业自动化领域具有独特的优势和广阔的应用前景[1]。

在农业收获作业中，传统刚性机械臂可应用于果类果实的采摘任务[2-5]，此外，在近年的研究中，菜类收获机械臂也相继产生[6-7]。采摘机械臂的设计过程中需根据作业对象的不同调整机构的构型和尺度设计，对作业任务需进行准确的运动学分析、路径规划[8-10]及综合性能的仿真研究[11-13]，而后利用合理的夹持机构完成果实的收获[14]。为提升收获类机械臂的自动化程度，通常结合视觉反馈系统等模块协调控制，进而增强其定位功能[15-19]。

相比于传统的刚性机械臂，连续体采摘机械臂具有良好的自适应性，配合具有相同柔性采摘功能的机械手可在复杂多变的作业环境中实现果蔬的采摘任务，且可极大地降低机械臂对作业环境中其他有益作物的破坏。然而，在采摘过程中，被夹持在连续体采摘机械臂末端的果蔬等负载导致具有良好柔性的采摘机械臂出现大幅变形，不利于其准确的完成果蔬收获作业的定位。

针对采摘作业的连续体机械臂，柔性特征在发挥其优势的同时，也存在刚度差的问题，制约了其在农业应用中的发展。其主要表现为连续体机械臂在末端夹持作业对象后，弹性变形大，变形姿态非线性程度高，计算求解困难，最终导致其运动精度难以保证。为此近年来诸多学者着眼于连续体机械臂的运动性能、承载性能和刚度等方面展开了研究，但至今仍是一个开放性的课题。

Walker等提出了不同结构形式的连续体机械臂的系统性运动学理论[20-22]，运动学理论的提出奠定了静力学和动力学理论系统建立的重要基础，然而在运动过程中，连续体机械臂自身质量及承载极大影响着其运动精度和运动性能，主要体现在柔性承载变形方面，所以单纯的运动学理论并不能满足连续体机械臂的运动精度要求。随着柔性理论的进一步发展，Mahvas等针对连续体手术机械臂的刚度进行了系统性研究[23]，进而基于刚度控制的连续体机械臂对未知环境影响的理论被提出[24]。刚度控制是连续体机械臂力学性能的研究前提，在此基础之上Chikhaoui等基于cosserat-rod理论提出了连续体机械臂的静力学模型[25-26]。此后，相继提出了筋驱动连续体机械臂的动力学理论及承载静力学理论[27-31]。综上，近年提出的力学模型多以筋型连续体机械臂为载体，而对于杆型连续体机械臂，现有理论模型并不能满足其变形姿态的控制，尤其在杆型连续体机械臂末端置有负载的状态下，其变形姿态的预测更是精确控制其运动的关键。针对以上问题，本文对具有全柔性特征的连续体采摘机械臂的承载性能进行研究。

1 连续体采摘机械臂

1.1 连续体采摘机械臂的主体结构

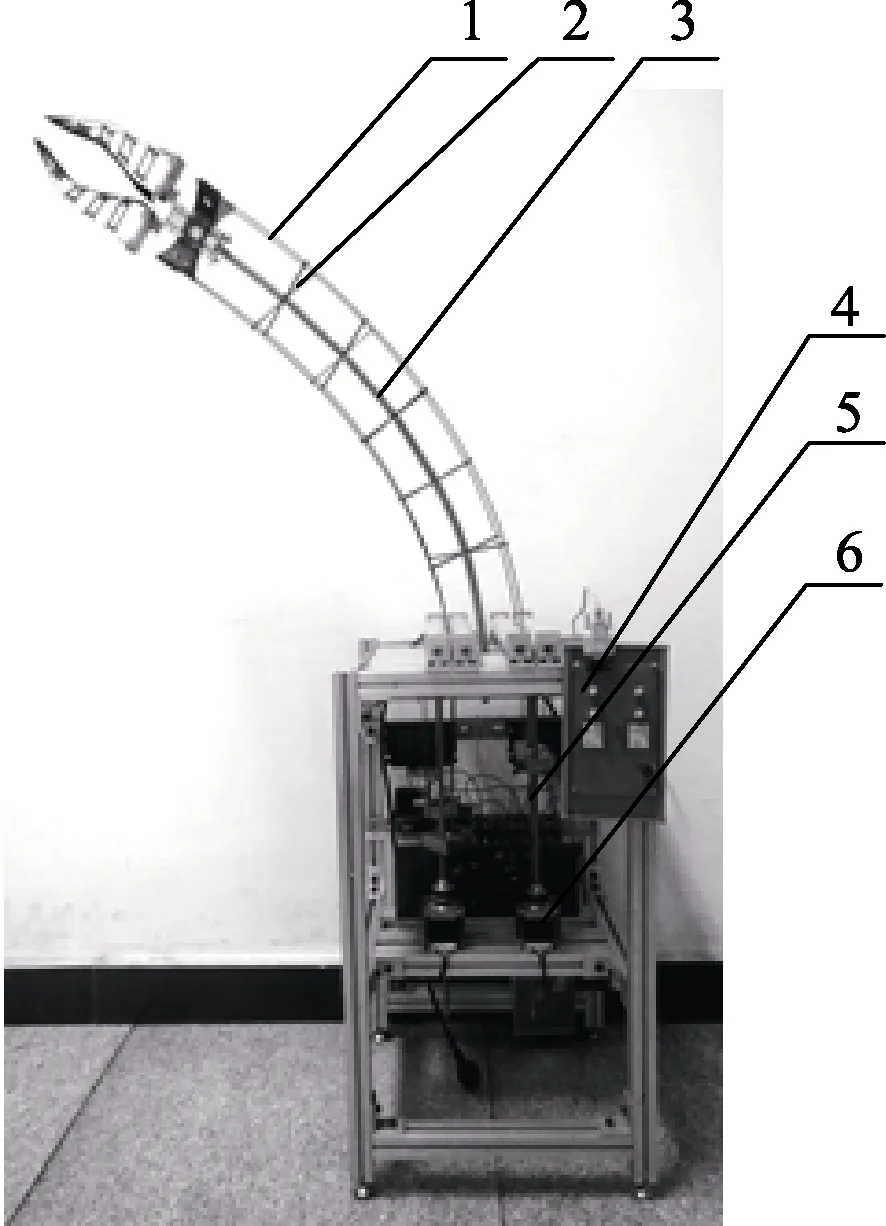
图1 连续体采摘机械臂样机Fig.1 Continuum picking manipulator prototype

连续体机械臂样机及主要部件如图 1所示，连续体采摘机械臂的结构是由玻璃纤维杆、引导架及橡胶套管组成，下部为相配套的驱动模块，主要包含运动控制卡、滚珠丝杠及伺服电机。连续体机械臂的主体是由5根直径2.5 mm的玻璃纤维杆构成，其弹性模量为3.26×104N/mm2连续体机械臂总体长度为800 mm，如图2a所示，其中4根为外围驱动杆，中间的为中心支撑杆。机械臂上均匀分布有引导架，材料为镁铝合金，尺寸如图2b所示, 其作用是保证连续体采摘机械臂的运动姿态为常曲率圆弧姿态, 4根外围驱动杆从其末端的孔中穿过，可在孔中自由滑动，引导架的间距通过安装在中心支撑杆上的等长的橡胶套管保证，间距为96.6 mm。

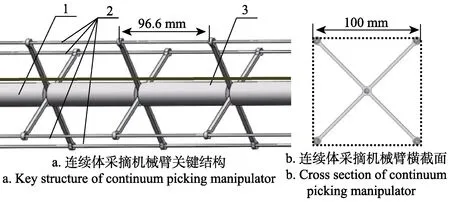
图2 连续体采摘机械臂结构示意图Fig.2 Structure diagram of continuum picking manipulator

1.2 驱动模块

连续体采摘机械臂的空间运动是由 4部伺服电机协调控制 4根外围驱动杆实现，中间支撑杆随动，电机型号为YZ-57BLS120（杭州翼志科技，功率为120 W，扭矩为330 N·mm，额定电压24 V，额定转速为3 000 r/min，最高精度为0.1 mm），控制单元由运动控制卡配合控制程序进行各种姿态的变化，其型号为 USB1020（阿尔泰科技，USB总线4轴运动控制卡，脉冲输出频率误差小于0.1%，脉冲输出速度最高可达4 MHz）。

利用伺服电机驱动滚珠丝杠旋转，进而控制各外围驱动杆伸出的长度实现整体连续体机械臂弯曲、回转等位姿的控制。

2 连续体采摘机械臂运动学模型

建立如图 3所示位姿空间体系，以连续体采摘机械臂的底部中心为坐标原点，根据其运动模式及驱动原理，可知其执行端运动学模型如式（1）。

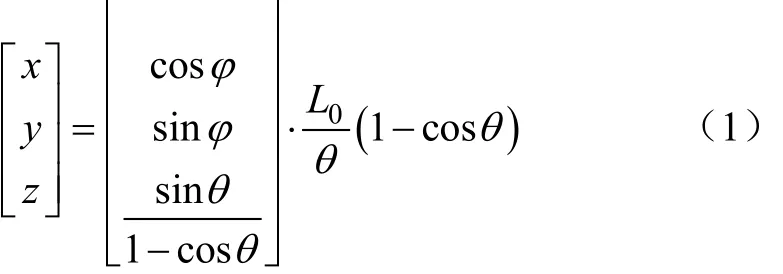
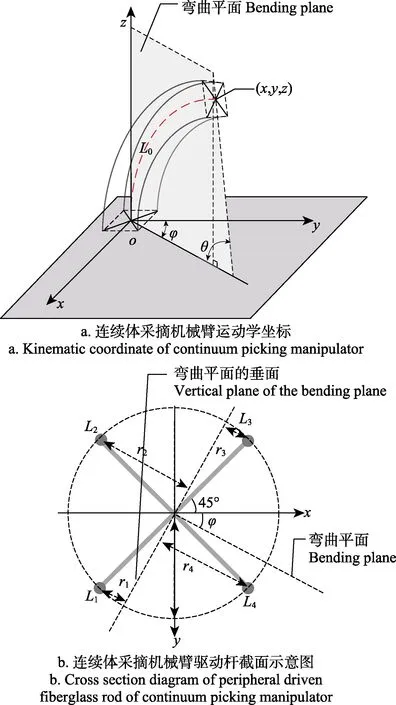
图3 连续体采摘机械臂运动及驱动原理Fig.3 Kinematic and driven principle coordinate of continuum picking manipulator

取连续体采摘机械臂横截面投影，建立如图3b的坐标系，驱动空间模型如式（2），其中 Li为各外围驱动杆的长度，L0为连续采摘柔性臂的长度即中心支撑杆长度，ri为底部引导架端点距离旋转后的轴线的距离。

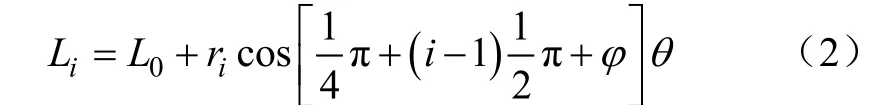
进而可得达到不同弯曲角和旋转角姿态时外围驱动杆所需的伸长、缩短量如式（3）。当LΔ为正值时外围驱动杆伸长，反之缩短。

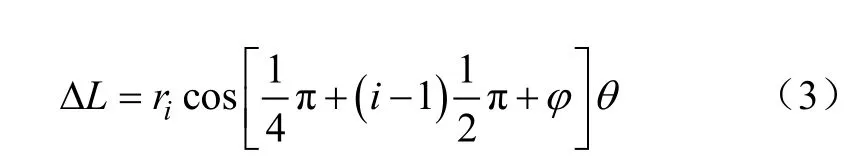
根据连续体采摘机械臂的式（1），给定弯曲角θ、旋转角φ的范围为[0,2π]，长度L0为800 mm，利用Matlab软件可做出连续体机械臂末端的运动范围，其为一心形曲面，四分之一剖面图如图 4所示。连续体采摘机械臂的运动作业过程中，配合底部移动平台可在作业环境中抓取一定空间范围内的果蔬。

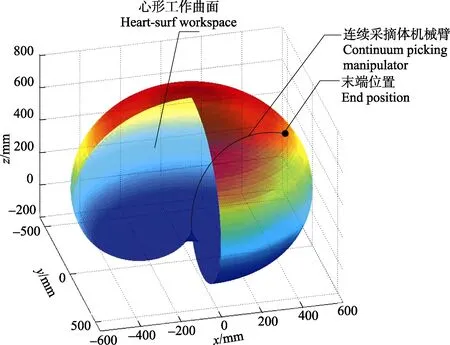
图4 连续体采摘机械臂的理论运动空间Fig.4 Theoretical kinematic workspace of continuum picking manipulator

3 连续体采摘机械臂承载模型的建立

3.1 连续体采摘机械臂的模型简化

根据连续体采摘机械臂的弯曲运动特性可知，其整体弯曲姿态趋近为常曲率圆弧，且引导架与外围驱动杆的相互作用力可作为系统内力，故在理论分析中连续体采摘机械臂的结构可简化为仅含顶端引导架的结构形式，外围驱动杆及中间支撑杆的姿态一致并保持常数曲率的柱体。

对简化后的连续体采摘机械臂进行弯矩平衡力学分析如图 5，坐标系{xoy}为连续体采摘机械臂的底部平面的坐标系，坐标系{x′oy′}为连续体采摘机械臂旋转角φ后的底部平面坐标系。坐标系{xeoye}为连续体采摘机械臂顶部平面坐标系，坐标系{x′eoy′e}为连续体采摘机械臂旋转φ角后的顶部平面坐标系。由静力学平衡方程，外部驱动力Fi(i=1,2,3,4)的平衡方程可得式（4），其中外部电机驱动力是未知的，所以在理论分析过程当中需将其替代。为建立标准的运动学模型，将底部作用在驱杆上的外部驱动力Fi转化至连续体采摘机械臂末端。因为外部驱动力Fi可沿驱动杆传递至末端，继而作用在顶部引导架上形成弯矩。

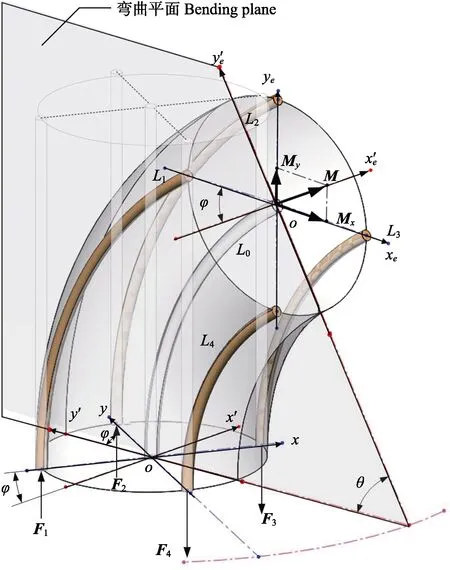
图5 连续体采摘机械臂的静力学分析Fig.5 Static analysis of continuum picking manipulator

在xe方向上的弯矩Mx是由外部驱动力F2和F4作用在末端引导架上形成，且方向是垂直于 ye轴，包含在由驱动杆L2和L4所构成的平面内，单位为N·mm。同理可知My。弯矩之和M垂直于连续体采摘机械臂弯曲姿态所在的弯曲平面，且弯矩之和M是弯矩Mx和弯矩My的矢量和

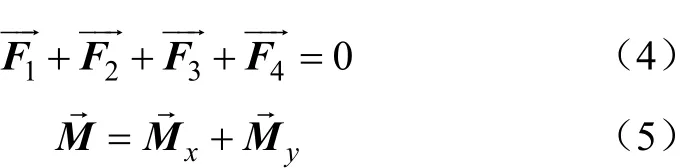
根据力学分析可求得弯矩Mx和弯矩My

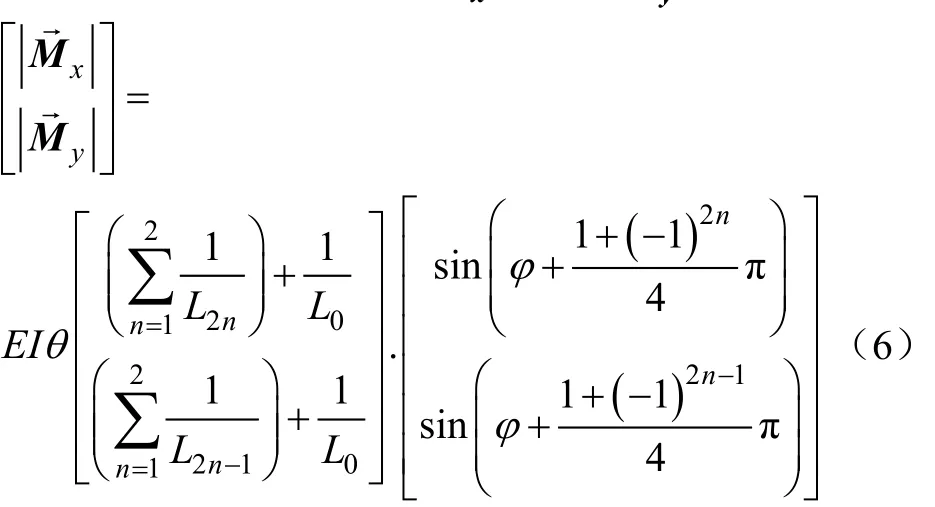
式中EI为玻璃纤维棒的抗弯刚度，N·mm2，E为玻璃纤维棒的弹性模量，N/mm²，I为外围驱动杆的对中心位置的惯性矩，mm4。

由于计算Mx和My时，重复计算了L0的弯矩值，所以需减去，固整理可得整体弯矩M如

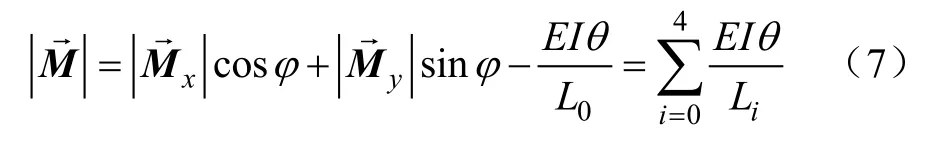
经过简化，将连续体采摘机械臂的底端驱动力转化为末端受弯矩的形式，将未知的驱动力转化为驱动弯矩。

3.2 连续体采摘机械臂的大挠度变形

假设连续体采摘机械臂的整体为一圆弧曲梁如图 6所示，曲率半径为R，可由弧长定理求得

根据前章节的驱动转化，其末端作用一个弯矩且该弯矩的方向垂直于连续体采摘机械臂弯曲时所在平面。由此根据纯弯曲公式可得连续采摘机械臂的等效抗弯刚度为

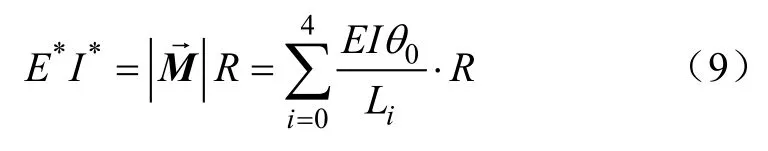
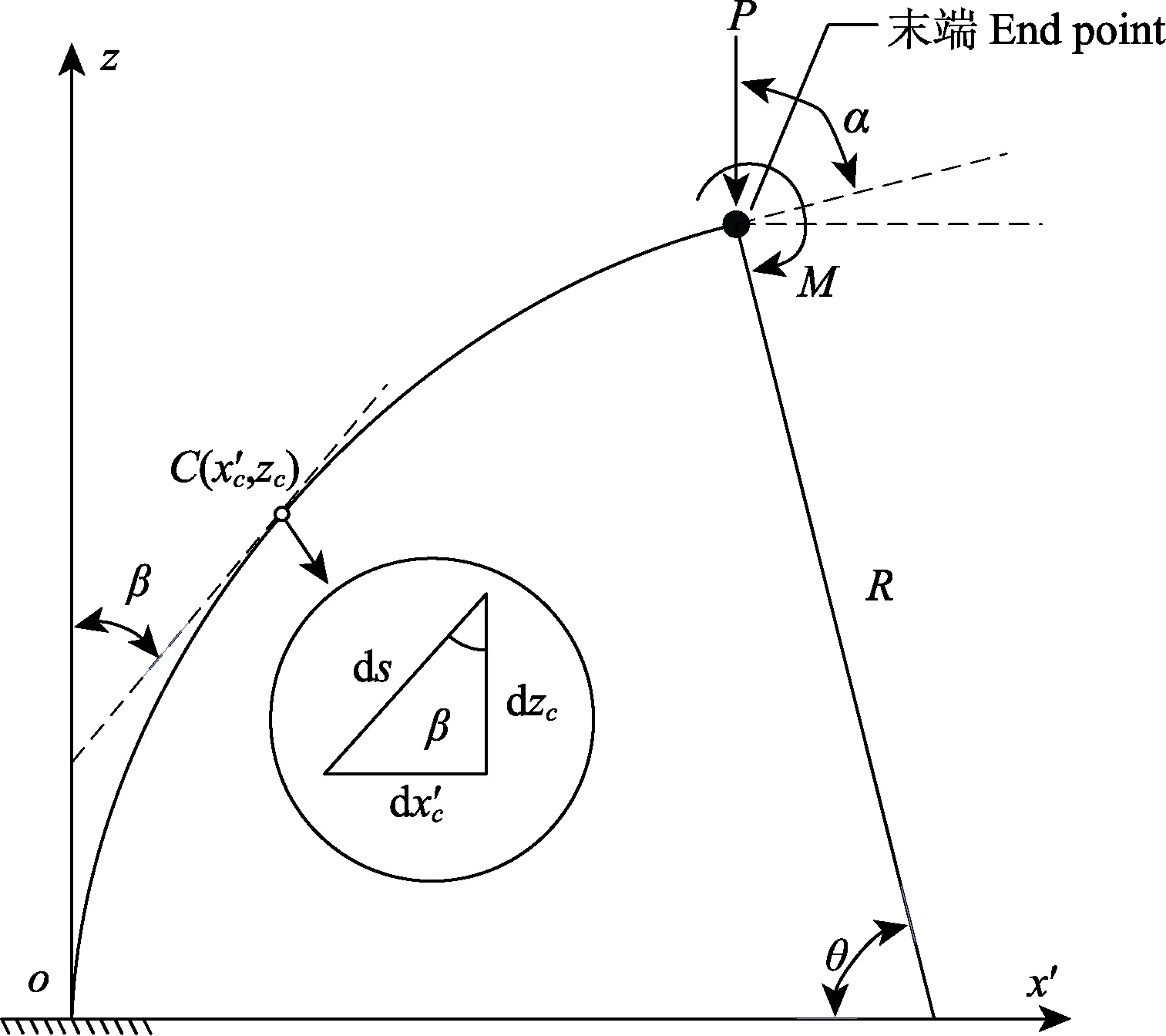
图6 连续体采摘机械臂在弯曲平面投影示意图Fig.6 Projection diagram of bending plane of continuum picking manipulator

对于连续采摘机械臂上任意一点C(x′c,zc)，根据大挠度理论[32]可得式（10）和（11），其中α为连续体采摘机械臂末端切线方向与z轴的夹角，β为在连续体采摘机械臂上任意一点C的切线方向与z轴的夹角，M（N·mm）和P（N）分别为作用在末端的弯矩和负载载荷。

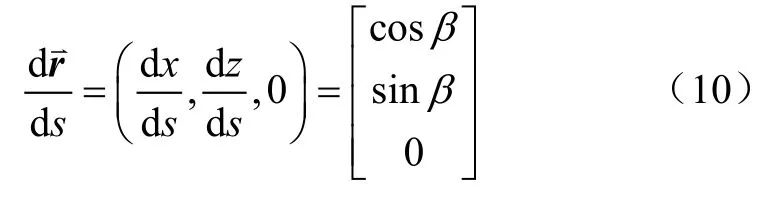
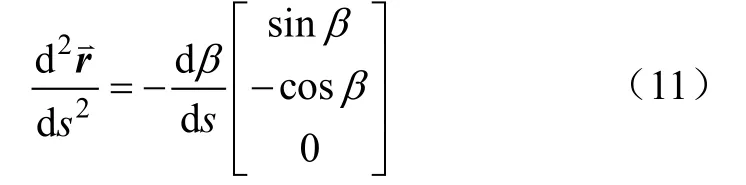
r是自坐标系原点至连续体采摘机械臂上任意点的矢径，ds为连续体机械臂上一微段弧长。可以推导得到式（12）。

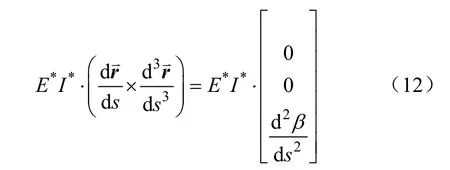
在任意点C截面上的内力矢为

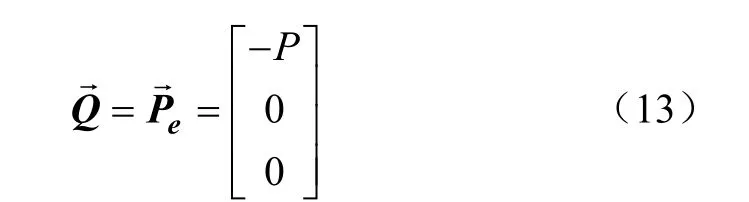
式中Q为内力矢，Pe为外力矢，利用杆件弯曲平衡原理以及式（13）并对β 积分可以得到

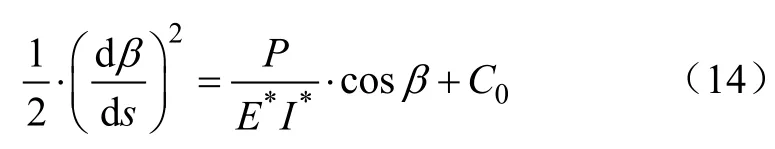
式中C0为积分常数，可利用边界条件求得，边界条件为：当β=α时，连续体采摘机械臂末端的曲率为将该边界条件代入式（14）后可得

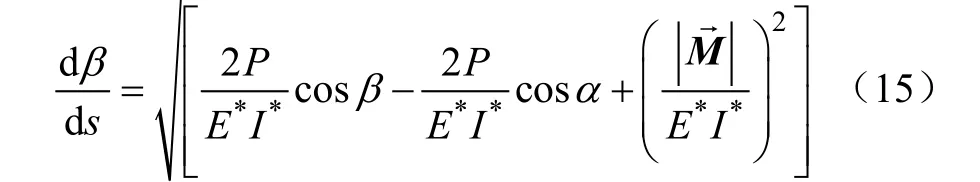
式（15）表征了连续体采摘机械臂弯曲时，臂上任意一点的曲率与β、α的函数关系，另一方面利用三角函数关系可知

将式子（16）代入方程（15）并整理可得，连续体采摘机械臂上任意一点在x’方向上的位移微段

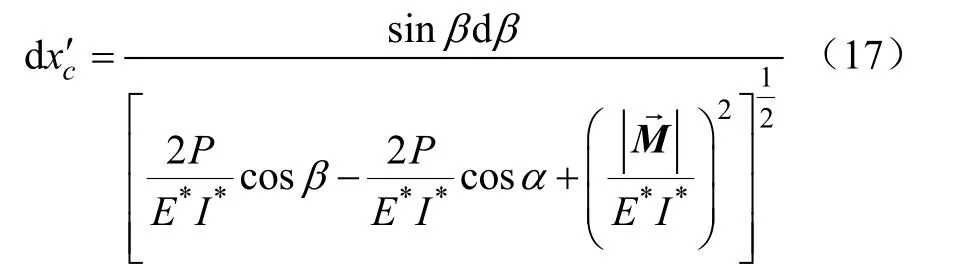
为方便求解方程，定义新的参数P*、Q和δ

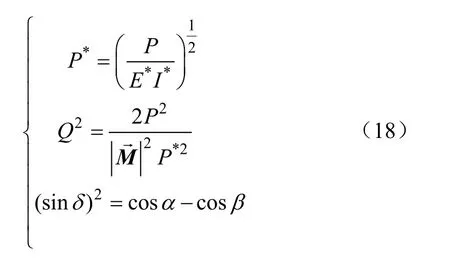
利用定义参数并积分整理得到方程（19），因此连续体采摘机械臂上任意点C的水平坐标x′c可表达为

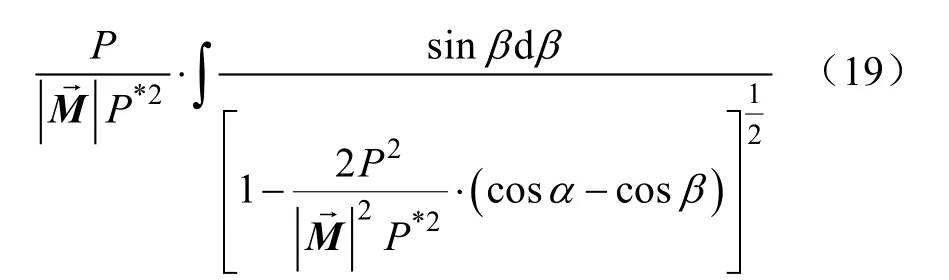
以δ为自变量对方程（18）进行求导可得dβ的方程

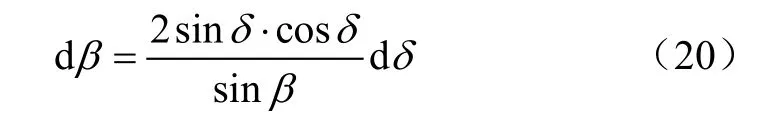
将dβ代入（19）整理可得

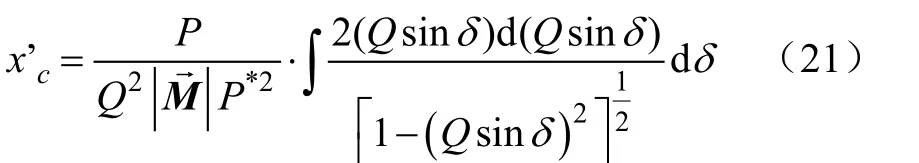
对式（21）进行积分，并根据边界条件当 β=0时，此时固定端的水平位移为 x′c=0。可得在连续体采摘机械臂上任意点C在水平坐标位置

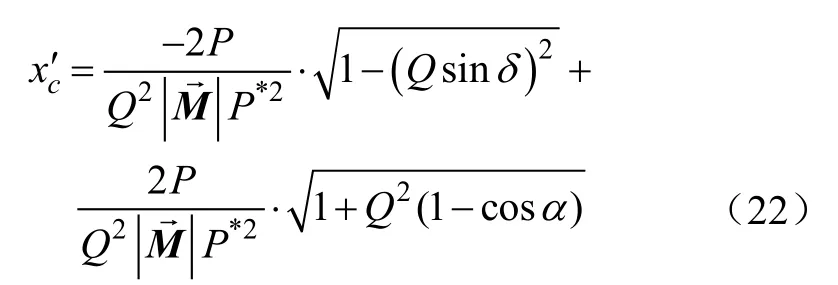
在求连续体采摘机械臂上任意一点纵坐标时，定义参数U、V和A

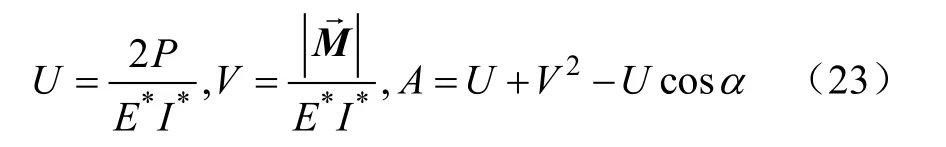
连续体采摘机械臂上任意一点C的竖直方向坐标可由积分式（24）变换整理并积分求得

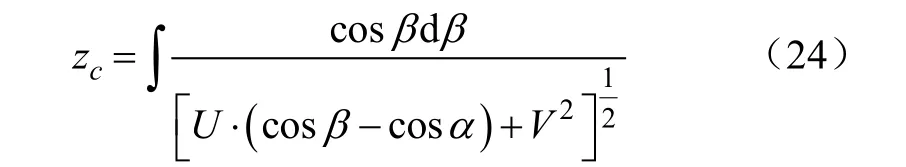
积分可得

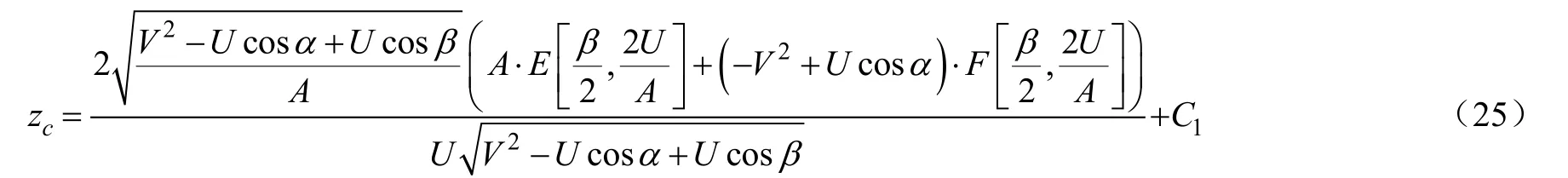
积分常数1C可利用边界条件

得到

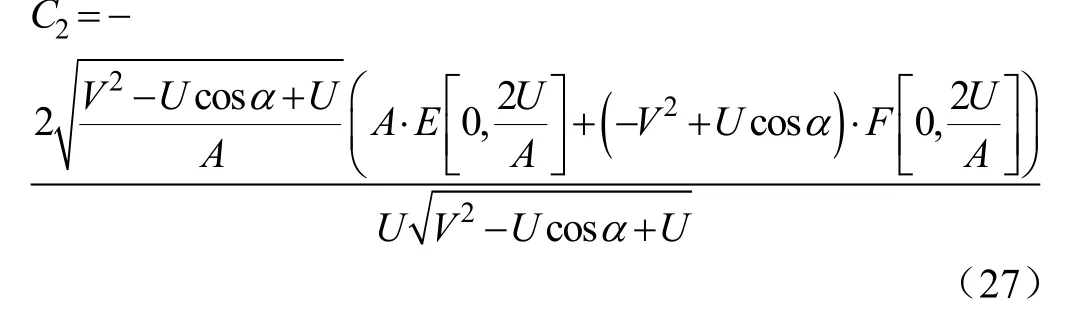
所以最终任意连续体采摘机械臂受末端负载载荷 P时臂上的任一点C的坐标

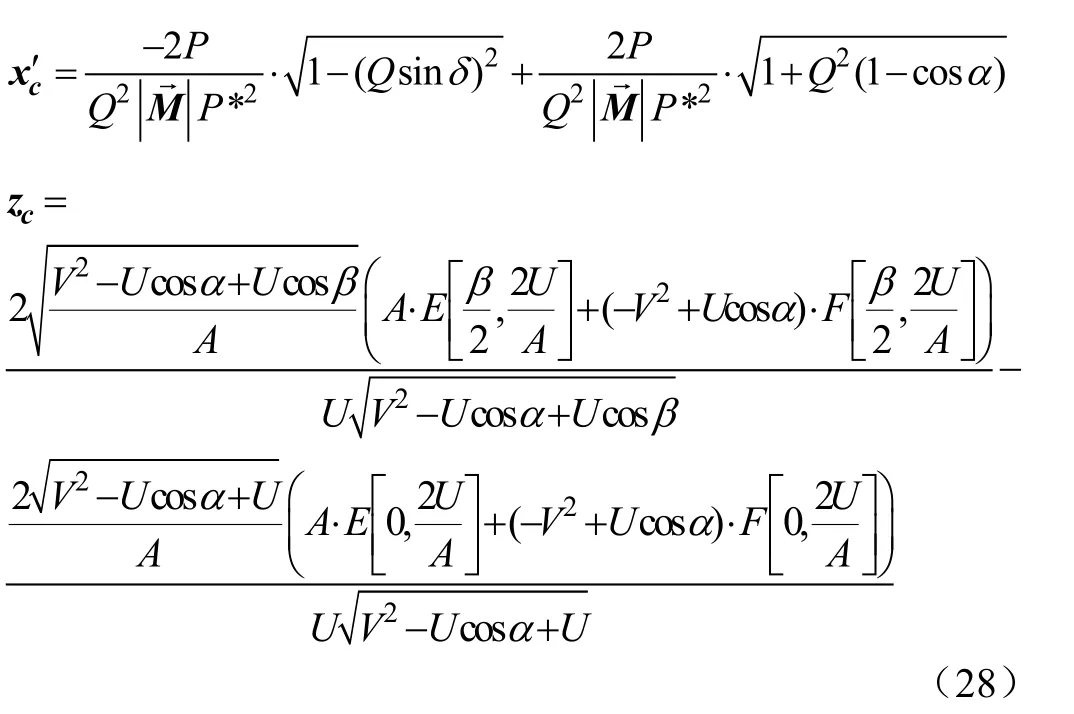
由于连续体采摘机械臂在无承载下的姿态为常曲率圆弧，弯曲角为θ，其末端负载载荷为P，在施加载荷P后弯曲角由θ变化为θp如图7，利用单位力原理可以求得变化后的弯曲角θp。

图7 连续体采摘机械臂承载简化模型Fig.7 Simplified loading model of continuum picking manipulator

如图 7所示，设在圆弧曲杆即图中所示空载位姿顶点有一水平单位F0和一单位弯矩mf，其值为0。水平单位力F0的方向平行于xoy平面且在弯曲平面内，单位弯矩fm 的方向垂直于弯曲平面。定义弯曲角θp和弯曲角θ的差值为θδ如式（29）。

对于弯曲变形后的连续体采摘机械臂，在任意点 C的弯矩平衡方程，θd为角度积分变量。

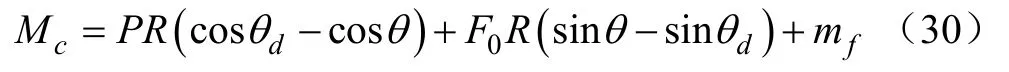
将方程（30）对单位弯矩mf微分可得

由单位力原理，列θδ的积分并积分可得

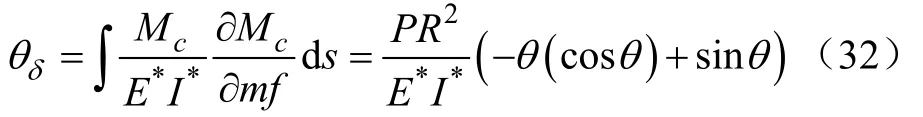
所以，由式（32）可得加载前后弯曲角的差值 θδ，利用方程（29）便可求得加载后的弯曲角θp如式（33），需已知的参数为

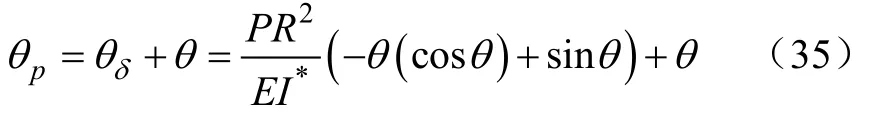
得到加载后的弯曲角θp后，将已知参数载荷P和θp代入方程（28），其中θp对应式（28）中α，便可得到加载后的连续体采摘机械臂顶点及其整体姿态的坐标。

4 连续体采摘机械臂承载模型验证

4.1 连续体采摘机械臂的承载试验系统

利用连续体采摘机械臂承载试验系统对加载后连续体采摘机械臂姿态位置变化进行静态性能研究如图 8a。机械臂的总体长度为 800 mm，驱动杆均布在边长为100 mm的正方形的 4个顶点，玻璃纤维杆的抗弯刚度1.254×105N ·mm2。为了保证试验的准确性，所有静态姿态实验数据的获取均在连续采摘机械臂已经稳定的情况下完成。

试验中加载试验方式为悬置砝码于连续体采摘机械臂末端，通过50 mm焦距高清无畸变摄像机，型号为AOS S-MIZE HD v2（瑞士AOS，采样率500 fps，分辨率为1280*720 dpi）如图8b记录不同负载载荷下的机械臂的弯曲变形姿态。外围驱动杆的最大伸长、收缩量为150 mm，设定旋转角φ为0，连续体采摘机械臂在弯曲平面内做弯曲姿态变形。自初始竖直状态开始，设定外围驱动杆L1、L2的伸长量和L3、L4的缩短量为60 mm，并通过运动控制卡控制电机驱动滚珠丝杠实现伸长、缩短量的控制，使连续体采摘机械臂弯曲，而后分别在末端置入50、100、150g砝码并利用摄像机记录连续体采摘机械臂此时的姿态。而后调整外围驱动杆L1、L2的伸长量和L3、L4的缩短量至最大值150 mm，重复上述试验。进一步，保持末端负载为100 g，分别调整外围驱动杆L1、L2的伸长量和L3、L4的缩短量为30、90、150 mm，记录姿态。最后利用软件将相机所采集的图片信息转化为连续体采摘机械臂上各点数据信息，并与相同参数下的理论计算数值进行比对。

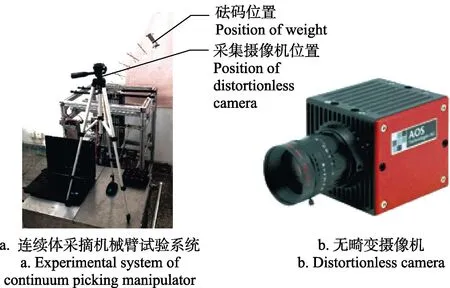
图8 连续体采摘机械臂试验系统Fig.8 Experimental system of continuum picking manipulator

4.2 结果与分析

通过试验，对比了对连续体采摘机械臂负载后的理论末端位置与试验末端位置的误差，验证了连续体采摘机械臂末端负载姿态理论模型。并利用参数试验的方法研究了弯曲姿态、负载载荷对末端位置误差的影响。

伸长、收缩量为60 mm，承载50～150 g的试验理论姿态对比结果如图9a所示。理论模型姿态与试验姿态相符，误差小于7.8%。当负载载荷为50 g时，理论模型姿态与试验姿态末端位置误差为4.7%，随着承载的增加，负载载荷为 150 g时理论模型姿态与试验姿态末端位置误差为7.8%。

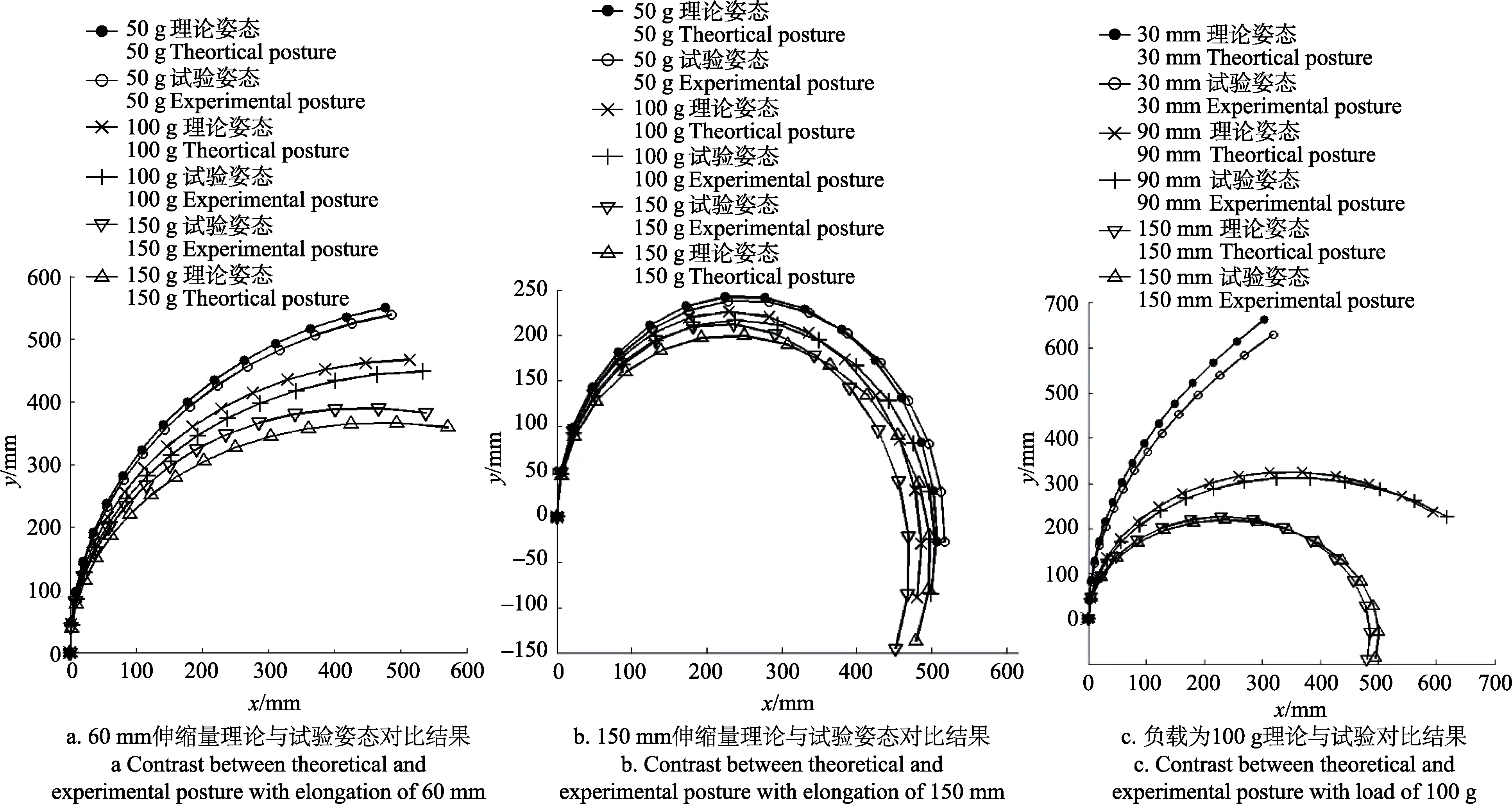
图9 连续体采摘机械臂在不同伸缩量和末端负载下的理论姿态与试验姿态对比结果Fig.9 Result of contrast between theoretical and experimental posture of continuum picking manipulator with different elongation and load

伸长、收缩量为150 mm，负载载荷为50 ～150 g的理论与试验姿态对比结果如图9b所示。同样地，当负载为 50 g时，理论模型姿态与试验姿态末端位置误差为3.8%，负载载荷为150 g时理论模型姿态与试验姿态末端位置误差为7.2%。

承载为100 g，伸长量为30、90、150 mm，从试验结果如图 9c，随着伸长量的增加，连续体采摘机械臂的理论与试验的姿态的误差减小，误差值分别为 6.5%、4.7%、4.4%。

从连续体采摘机械臂的承载试验中可知，无论伸长量大小如何，当末端承载增加时，理论试验姿态的误差逐渐增加，其主要原因为当承载增加时，连续体采摘机械臂向前倾覆的程度增大，由重力导致悬臂梁效应增大，致使误差逐渐增大。

而当负载不变时，随着伸长量的增加，连续体采摘机械臂的理论模型姿态与试验姿态末端位置误差渐小。由连续体采摘机械臂的特性可知，随着伸长量的增加，其总体刚度随机械臂弯曲姿态程度增大而增加，所以在刚度增大的条件下，其受自身质量产生的重力影响会逐渐降低，故出现随伸长量的增加误差减小的现象。

5 结 论

1）本文系统地分析了应用于农业的连续体采摘机械臂的驱动及承载变形原理，转化了其在理论模型建立中的驱动形式，进而提出了一种结合挠度变形理论和单位力法则的简化算法，并完成了连续体采摘机械臂承载姿态变形的数学模型的建立，为其采摘作业姿态变形的控制提供了良好的理论基础。

2）本文在建立连续体采摘机械臂承载姿态变化理论模型中，将复杂的非线性连续体采摘机械臂简化为一种圆弧曲杆，极大地降低了对该刚-柔系统分析的复杂性和计算量，并且通过试验验证了理论的有效性，其理论模型与试验结果的误差均小于7.8%。

3）分析了连续体采摘机械臂弯曲姿态控制参数和末端负载载荷对理论模型姿态与试验姿态末端位置误差影响的规律，为在复杂作业环境中，科学地选取连续体采摘机械臂的运动范围和姿态调整提供了可靠的理论依据。

[1] 高国华，杨行，韦康成，等. 全柔性机械臂的实验模拟分析[J]. 中国农机化学报，2013，34(3)：108－111.Gao Guohua, Yang Hang, Wei Kangcheng, et al. Experimental simulation of the flexible robot manipulators[J]. Journal of Chinese Agricultural Mechanization, 2013, 34(3): 108－111.(in Chinese with English abstract)

[2] 王海峰，李斌，刘广玉，等. 菠萝采摘机械手的设计与试验(英文)[J]. 农业工程学报，2012，28(2)：42－46.Wang Haifeng, Li Bin, Liu Guangyu, et al. Design and test of pineapple harvesting manipulator[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2012, 28(2): 42－46. (in Chinese with English abstract)

[3] 王丽丽，范晋伟，赵博，等. 果蔬采摘机械臂结构设计与性能测试[J]. 农业工程，2017，7(2)：107－113.Wang Lili, Fan Jinwei, Zhao Bo, et al. Structural design and performance test of fruit and vegetable picking manipulator[J].Agricultural Engineering, 2017, 7(2): 107－113. (in Chinese with English abstract)

[4] 赵东辉，张慧. 基于自动控制技术的多手臂水果采摘装置的设计[J]. 农机化研究，2015(9)：135－138.Zhao Donghui, Zhang Hui. Based on the automatic control of agricultural manipulator with many arms design[J]. Journal of Agricultural Mechanization Research, 2015(9): 135－138.(in Chinese with English abstract)

[5] 董芒，顾宝兴，姬长英，等. 水果采摘机器人智能移动平台的设计与试验[J]. 华南农业大学学报，2016，37(4)：128－133.Dong Mang, Gu Baoxing, Ji Changying, et al. Design and experiment of an intelligent mobile platform loaded with a fruit picking robot[J]. Journal of South China Agricultural University, 2016, 37(4): 128－133. (in Chinese with English abstract)

[6] 吴玉娟，刘永华. 基于机械手臂的叶菜有序收获机械设计与实现[J]. 江苏农业科学，2016，44(12)：353－355.Wu Yujuan, Liu Yonghua. Design and implementation of orderly harvesting machinery for leafy vegetables based on mechanical arm[J]. Jiangsu Agricultural Sciences, 2016,44(12): 353－355. (in Chinese with English abstract)

[7] 孙学岩. 谈蔬菜自动化收获机械研究现状[J]. 农业机械，2008(11)：43－43.Sun Xueyan. Research status of automatic harvesting machinery for vegetables[J]. Agricultural Machinery, 2008(11): 43－43.(in Chinese with English abstract)

[8] 阳涵疆，李立君，高自成. 基于关节构形空间的混联采摘机械臂避障路径规划[J]. 农业工程学报，2017，33(4)：55－62.Yang Hanjiang, Li Lijun, Gao Zicheng. Obstacle avoidance path planning of hybrid harvesting manipulator based on joint configuration space[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE),2017, 33(4): 55－62. (in Chinese with English abstract)

[9] 刘忠超，熊雷，翟天嵩. 六自由度采摘机械臂系统设计[J].农机化研究，2015(8)：112－114.Liu Zhongchao, Xiong Lei, Zhai Tiansong. Design of six degree of freedom picking manipulator[J]. Journal of Agricultural Mechanization Research, 2015(8): 112－114. (in Chinese with English abstract)

[10] 卢君宜，熊晓松，朱东. 五自由度采摘机械臂关节空间轨迹规划[J]. 轻工机械，2013，31(4)：11－14.Lu Junyi, Xiong Xiaosong, Zhu Dong. Trajectory planning of 5-dof picking manipulator in joint space[J]. Light Industry Machinery, 2013, 31(4): 11－14. (in Chinese with English abstract)

[11] 吕政昂. 采摘机器人机械臂设计[J]. 自动化应用，2017(8)：1－4.Lü Zhengang. Design of manipulator for picking robot[J].Automation Applications, 2017(8): 1－4. (in Chinese with English abstract)

[12] 马强，陈志，张小超，等. 基于ADAMS的果树采摘机械臂的运动仿真分析[J]. 农机化研究，2013(5)：37－40.Ma Qiang, Chen Zhi, Zhang Xiaochao, et al. Motion simulation analysis of harvesting robot arm based on adams[J]. Journal of Agricultural Mechanization Research, 2013(5): 37－40.(in Chinese with English abstract)

[13] 高自成，李立君，刘银辉. 油茶果采摘机采摘机械臂的机构设计及运动仿真[J]. 西北林学院学报，2012，27(2)：266－268.Gao Zicheng, Li Lijun, Liu Yinhui, The mechanism design and movement simulation for the mechanical arm of the oil-tea camellia fruit picking machine[J]. Journal of Northwest Forestry University, 2012, 27(2): 266－268. (in Chinese with English abstract)

[14] 胡志勇，张学炜，张伟，等. 西瓜采摘末端执行器夹持力精确控制[J]. 农业工程学报，2014，30(17)：43－49.Hu Zhiyong, Zhang Xuewei, Zhang Wei, et al. Precise control of clamping force for watermelon picking endeffector[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(17): 43－49. (in Chinese with English abstract)

[15] 熊俊涛，邹湘军，陈丽娟，等. 采摘机械手对扰动荔枝的视觉定位[J]. 农业工程学报，2012，28(14)：36－41.Xiong Juntao, Zou Xiangjun, Chen Lijuan, et al. Visual position of picking manipulator for disturbed litchi[J].Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2012, 28(14): 36－41. (in Chinese with English abstract)

[16] 王丹丹，徐越，宋怀波，等. 基于平滑轮廓对称轴法的苹果目标采摘点定位方法[J]. 农业工程学报，2015，31(5)：167－174.Wang Dandan, Xu Yue, Song Huaibo, et al. Localization method of picking point of apple target based on smoothing contour symmetry axis algorithm[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(5):167－174. (in Chinese with English abstract)

[17] 王粮局，张立博，段运红，等. 基于视觉伺服的草莓采摘机器人果实定位方法[J]. 农业工程学报，2015，31(22)：25－31.Wang Liangjü, Zhang Libo, Duan Yunhong, et al. Fruit localization for strawberry harvesting robot based on visual servoing[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(22):25－31. (in Chinese with English abstract)

[18] 王丹丹，宋怀波，何东健. 苹果采摘机器人视觉系统研究进展[J]. 农业工程学报，2017，33(10)：59－69.Wang Dandan, Song Huaibo, He Dongjian. Research advance on vision system of apple picking robot[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(10): 59－69. (in Chinese with English abstract)

[19] 罗陆锋，邹湘军，熊俊涛，等. 自然环境下葡萄采摘机器人采摘点的自动定位[J]. 农业工程学报，2015，31(2)：14－21.Luo Lufeng, Zou Xiangjun, Xiong Juntao, et al. Automatic positioning for picking point of grape picking robot in natural environment[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015,31(2): 14－21. (in Chinese with English abstract)

[20] Walker I D, Hannan M W. A novel ‘elephant’s trunk’manipulator[J]. IEEE/ASME Int.conf.Advanced Intelligent Mechatronics, 1999, 3(1): 410－415.

[21] Jones B A, Walker I D. Kinematics for multisection continuum robots[J]. IEEE Transactions on Robotics, 2006, 22(1): 43－55.

[22] Bajo A, Simaan N. Kinematics-based detection and localization of contacts along multisegment continuum robots[J]. IEEE Transactions on Robotics, 2012, 28(2): 291－302.

[23] Mahvas M, Dupont P E. Stiffness control of surgical continuum manipulators[J]. IEEE Transactions on Robotics A Publication of the IEEE Robotics & Automation Society,2011, 27(2): 334－345.

[24] Goldman R E, Bajo A, Simaan N. Compliant motion control for multisegment continuum robots with actuation force sensing[J]. IEEE Transactions on Robotics, 2014, 30(4):890－902.

[25] Chikhaoui M T, Rabenorosoa K, Andreff N. Kinematics and performance analysis of a novel concentric tube robotic structure with embedded soft micro-actuation[J]. Mechanism& Machine Theory, 2016, 104(6): 234－254.

[26] Tunay İlker. Spatial continuum models of rods undergoing large deformation and inflation[J]. IEEE Transactions on Robotics, 2013, 29(2): 297－307.

[27] Rucker D C, Iii R J W. Statics and dynamics of continuum robots with general tendon routing and external loading[J].IEEE Transactions on Robotics, 2011, 27(6): 1033－1044.

[28] Falkenhahn V, Mahl T, Hildebrandt A, et al. Dynamic modeling of bellows-actuated continuum robots using the euler-lagrange formalism[J]. IEEE Transactions on Robotics,2015, 31(6): 1483－1496.

[29] Renda F, Giorelli M, Calisti M, et al. Dynamic model of a multibending soft robot arm driven by cables[J]. IEEE Transactions on Robotics, 2014, 30(5): 1109－1122.

[30] Jung J, Penning R S, Ferrier N J, et al. A modeling approach for continuum robotic manipulators: Effects of nonlinear internal device friction[C]//Ieee/rsj International Conference on Intelligent Robots and Systems. IEEE, 2011: 5139－5146.

[31] Gravagne I A, Walker I D. Manipulability, force, and compliance analysis for planar continuum manipulators[J].IEEE Transactions on Robotics & Automation, 2002, 18(3):263－273.

[32] 周凤玺，李世荣. 梁的弹塑性大挠度变形分析[J]. 兰州理工大学学报，2007，33(1)：170－172.Zhou Fengxi, Li Shirong. Analysis of beam deformation with elastic-plastic large deflection[J]. Jounal of Lanzhou University of Technology, 2007, 33(1): 170－172. (in Chinese with English abstract)