模糊需求环境下供应链广告策略研究
杨 侃,田双亮
(1.西北民族大学数学与计算机科学学院,甘肃兰州,730030;2.西北民族大学动态流数据计算与应用实验室,甘肃兰州,730030)
一、引言
广告作为一种被大众认可的产品信息传播方式广泛存在于供应链的多个环节之中,在供应链管理中供应链广告是一种不可获缺的营销机制和协调方式[1]。通过对众多文献研读和分析发现,供应链广告问题中涉及的主要方面有供应链成员广告活动参与水平、价格以及供应链利润及其分配等。如Huang 和 Li[2],Yue等[3],Szmerekovsky 和 Zhang[4],Xie和Neyret[5]采用非线性市场需求函数的形式讨论供应链广告博弈问题。Xieab和Wei(2009)[6],Kunter[7],Jørgensen 和 Zaccour[8]采用线性市场需求函数的形式讨论供应链广告博弈问题。在两类市场需求函数中,都无一例外的论了基本市场需求和价格敏感程度对供应链成员广告参与水平、价格以及供应链利润的影响。可见基本市场需求和价格敏感程度是决定供应链成员广告策略的重要因素。
然而,无论采用何种形式的市场需求函数,大多数文献都是将基本市场需求和价格敏感程度视为非模糊数值。而实际营销过程中由于消费者基本需求的认知偏差、价格敏感程度及其本身的模糊性,此类参数的大小难以用具体的数值度量。因此,本文以单个零售商和单个制造商组成的二级供应链模型为背景,用三角模糊数来刻画基本市场基本需求和价格敏感程度,运用模糊截集理论和博弈理论,在模糊环境下,讨论零售商和制造商纳什博弈模型中的最优广告策略和最优期望利润问题。
二、三角模糊集理论及其相关性质
Zadeh提出的模糊集理论是一种处理不确定性现象的有力工具[9]。此后,国内外众多学者在此基础上不断发展和完善模糊集理论,参考相关文献可得到以下相关定义和性质。
定义1[10]设有一个三角模糊数(TFN)u͂=(u1,u2,u3),其中,u1<u2<u3,u1,u3分别是u的上下界,u2为u的最可能取值,如图1所示。u͂的隶属度函数定义为:

当u1>0,则称u͂为正则三角模糊数。如果u1=u2=u3,则三角模糊数u͂退化成非模糊数u。
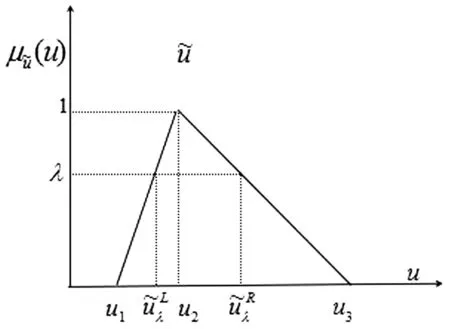
图1 三角模糊数及其对应的隶属度函数
定义2[11]设u͂为论域U上的一个模糊子集,任取λ∈[0,1],记u͂λ={x|μu͂(x)≥λ},称u͂λ为u͂ 的λ水平集,其中λ称为置信水平。u͂λ可表示为u͂λ=R:μu͂(x)≥λ} 分别为u͂λ的左边界和右边界。对于,三角模糊数u͂=(u1,u2,u3)的λ水平集(1-λ)u3。
根据定义1、定义2可得以下性质:
性质1 设u͂=(u1,u2,u3)为一个三角模糊数,对于 ∀λ∈[0,1],当x͂=(u͂)n,y͂=ku͂时,有

性质 2 设u͂=(u1,u2,u3),v͂=(v1,v2,v3)为两个三角模糊数,对于 ∀λ∈[0,1],当x͂=u͂+v͂ ,y͂=u͂ -v͂时,有

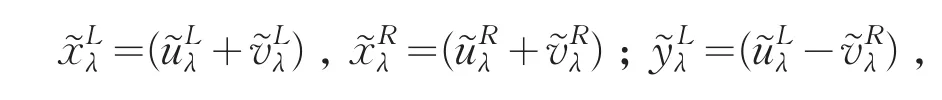
性质 3 设u͂=(u1,u2,u3),v͂=(v1,v2,v3)为两个三角模糊数,对于∀λ∈[0,1],k1,k2为两个非零常数且 (k1>0)∧(k2> 0),当时,有

定义 3[12]设u͂=(u1,u2,u3)是一个三角模糊数,,则三角模糊数期望为E[u͂]=
定义 4[13]设u͂=(u1,u2,u3),v͂=(v1,v2,v3)为两个三角模糊数,,则有∀a,b∈R,使得E[au͂+bv͂]=aE[u͂]+bE[v͂]。
三、博弈模型建立和求解
以单个零售商和单个制造商组成的二级供应链模型为背景,制造商的决策变量为产品批发价格w和全国性广告活动参与水平A,零售商的决策变量为产品零售价格p和地方性广告活动参与水平a,为了便于分析,假设零售商和制造商掌握的市场需求信息是对称的,它们之间的决策行为都是单周期内进行。参照文献[5,6]中相关假设和模型,市场需求函数形式为:
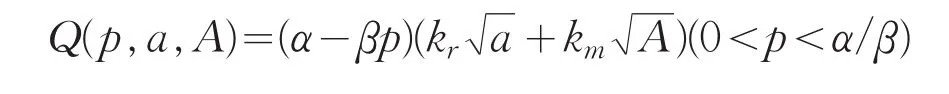
其中α为正的常数,其表示为市场基本需求,β为正的常数,表示为价格敏感程度;kr为正的常数,表示为零售商地方性广告活动的效应因子;km为正的常数,为制造商地全国性广告活动的效应因子。为确保有一个非负的市场需求函数,假定概率P((α-βp)<0)=0 。
然而,在现实的广告活动过程中,由于消费者基本需求的认知偏差,价格敏感程度及其本身的模糊性,市场基本需求与价格敏感程度往往表现出模糊性。因此,假设市场需求函数Q(p,a,A)中参数α和β是模糊的,其中ᾶ=(α1,α2,α3)(0<α1<α2<α3)和同时假设ᾶ 和β͂保持同一置信水平λ。因此,可得到模糊环境下的市场需求函数为:
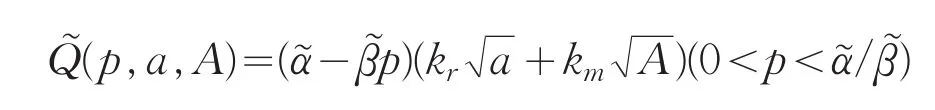
由上述市场需求函数,可得零售商和制造商模糊利润函数分别为:
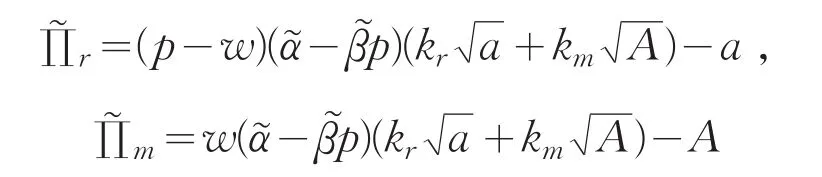
在纳什博弈模型中,遵从自身利益最大化原则下零售商确定产品零售价格p和地方性广告活动参与水平a,制造商确定产品批发价格w和全国性广告活动参与水平A。假设所有的博弈参与者都会得到一个非负的期望利润,因为任何一方的期望利润不大于零,则该模型就不具有可行性。结合定义3、4可得纳什博弈模型中零售商和制造商期望利润博弈模型分别为:
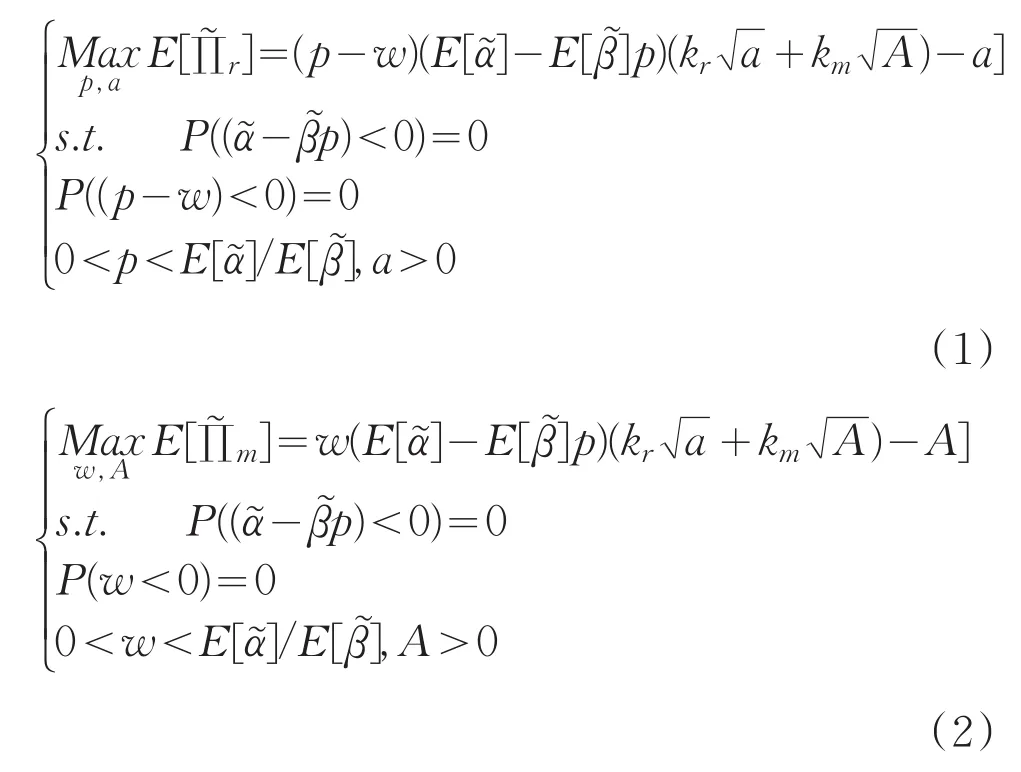
借鉴文献[5,14,15]中对相关函数的处理方法,当制造商的期望利润随着批发价格w增加而递增,当批发价格取得最大值 时制造商期望利润最大,而此时零售商的单位边际利润为零,在这种情况下零售商就失去了销售产品和投资广告的动力,所以,零售商单位利润必须大于等制造商的单位利润。因此,要求满足p-w≥w,即w≤p/2,所以令w=p/2。由(1)式、(2)式目标函数及其一阶最优条件和可得到零售商和制造商均衡策略分别为(p,a)和(w,A)。其中

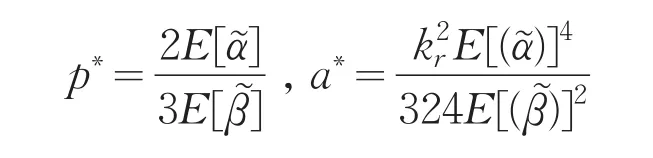

显然,H2>0,H2是负定矩阵。因此,制造商期望利润关于 (w,A)是凹函数,模型(2)存在唯一的均衡最优解(w*,A*),其中
综上,零售商和制造商的最优期望利润分别为:

四、数值算例和分析
根据以上运算规则和算式计算得到的供应链成员最优策略和最优期望利润,本部分使用数值算例的方法来分析相关参数变化对最优策略的影响以及模糊参数变动对最优期望利润的影响。
基本市场需求ᾶ和价格敏感程度的语义表达式与其三角模糊变量之间的关系如表1所示。

表1 语义表达式和三角模糊数之间的关系
根据表1,可得到基本市场需求ᾶ=(300,500,800),价格敏感程度,根据定义2和定义3可得的λ水平截集和期望值分别为:

(一)参数变化对最优策略的影响
根据表1可知,市场基本需求ᾶ=(300,500,800),价格敏感程度β͂=(30,60,80),利用MATLAB12验证在模糊参数低值和高值范围内,价格和广告活动参与水平变化情况,如图2和图3所示。

图2 价格变化
图2表示在三角模糊环境下,市场基本需求低值和高值分别取[300,800],价格敏感程度低值和高值分别取[30,80]时,批发价格和零售价格变化情况。处于较低位置的图形表示批发价格变化情况,较高位置的图形表示零售价格变化情况,它们之间的空间高度差额为零售商边际利润的大小。由图2可知,价格与市场基本需求正相关,与价格敏感程度负相关,并且,随着模糊参数取值位置的移动,零售商边际利润大小也不断变化,当市场基本需求取高值,价格敏感程度取低值时,零售商边际利润取得最大值。因此,针对价格敏感的产品,如价格标准比较低、价格信息传递较快以及品牌形象好的产品等,供应链决策者可适当的进行价格折扣,使得消费者形成价格知觉,以期获得更多利润。
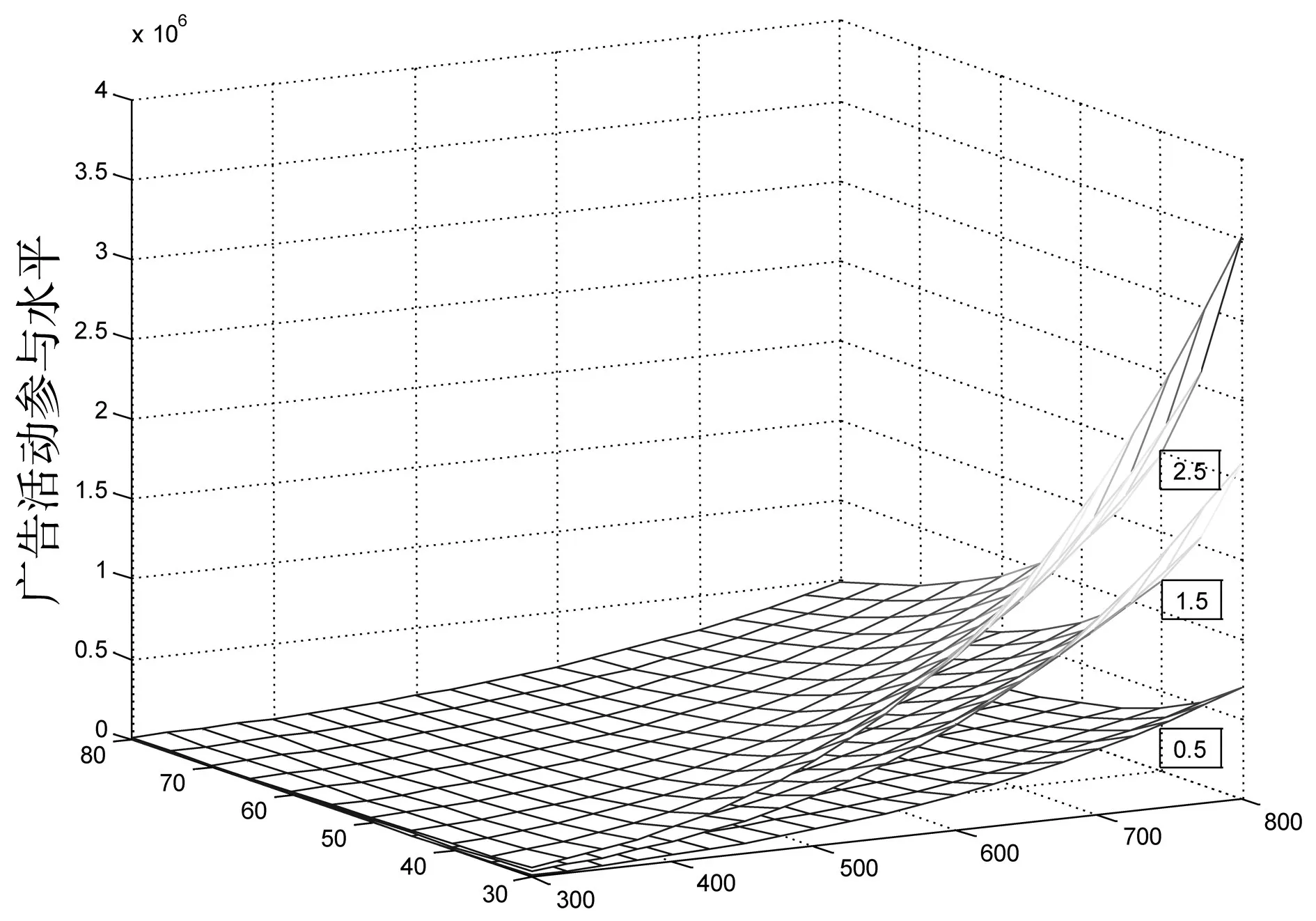
图3 零售商广告活动参与水平变化
图3表示在三角模糊环境下,市场基本需求低值和高值分别取[300,800],价格敏感程度低值和高值分别取[30,80],零售商广告活动效应因子kr分别取0.5、1.5和2.5时,零售商地方性广告活动参与水平a的变化情况。由图3可知,当kr=0.5时,a处于一个较低位置,随着kr取值的增加,a也随之递增,零售商广告活动效应因子kr与零售商地方性广告投入水平a正相关。制造商全国性广告参与水平与之相似,在此不作赘述。
结合(p*,a*)和(w*,A*),通过对图2和图3的分析可知:
1.在纳什博弈模型中,产品零售价格是其批发价格的2倍,价格与市场基本需求正相关,与价格敏感程度负相关,与广告活动效应无关。模糊环境下,供应链成员可参考市场已有信息,对利润预测和广告策略制定进行控制与调整。
2.在其他参数大小相同的条件下,广告活动效应与广告活动参与水平正相关,广告活动效应大小直接决定了供应链成员参与广告活动的水平和积极性。此外,对比A∗和a∗可知,若km=kr,则制造商全国性广告活动参与水平与零售商地方性广告活动参与水平相同,若km>kr,则制造商全国性广告活动参与水平大于零售商地方性广告活动参与水平。若km<kr,则制造商全国性广告活动参与水平小于零售商地方性广告活动参与水平。
(二)模糊参数变动对最优期望利润的影响
根据表2与表3,利用MATLAB12验证参数ᾶ的低值与高值数值变化对零售商和制造商最优期望利润变化的影响情况,如图4和图5所示
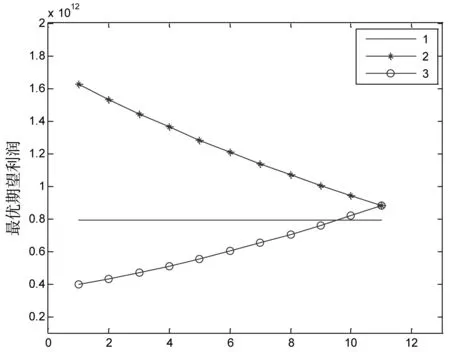
图4 零售商最优期望利润变化情况
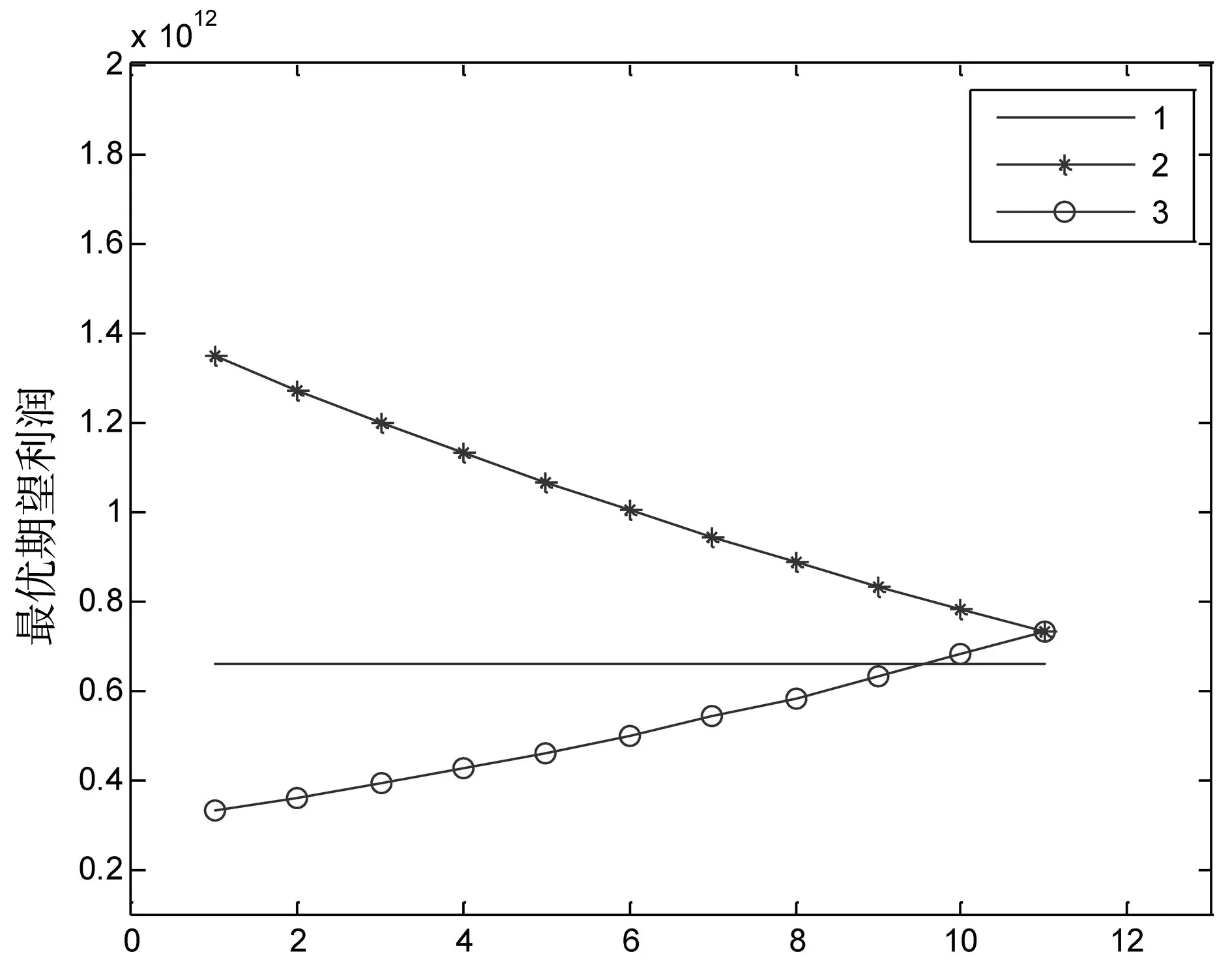
图5 制造商最优期望利润变化情况
表2 参数ᾶ和低值变化情况
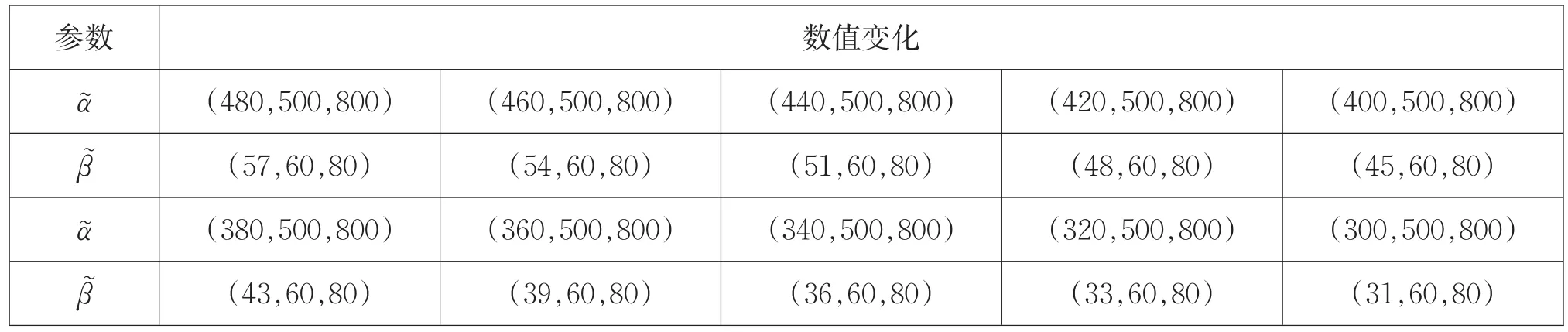
表2 参数ᾶ和低值变化情况
参数ᾶ β͂ ᾶ β͂数值变化(480,500,800)(57,60,80)(380,500,800)(43,60,80)(460,500,800)(54,60,80)(360,500,800)(39,60,80)(440,500,800)(51,60,80)(340,500,800)(36,60,80)(420,500,800)(48,60,80)(320,500,800)(33,60,80)(400,500,800)(45,60,80)(300,500,800)(31,60,80)
表3 参数ᾶ和高值变化情况

表3 参数ᾶ和高值变化情况
参数ᾶ β͂ ᾶ β͂数值变化(300,500,770)(30,60,78)(300,500,620)(30,60,68)(300,500,740)(30,60,76)(300,500,590)(30,60,66)(300,500,710)(30,60,74)(300,500,560)(30,60,64)(300,500,680)(30,60,72)(300,500,530)(30,60,62)(300,500,650)(30,60,70)(300,500,500)(30,60,60)
通过表2、表3,图4和图5的分析可知:
1.经过一系列运算规则和算式计算,模糊数值能够转化为非模糊数值并能与之对比分析,非模糊数值是模糊数值的一种特殊情况,而模糊数值更具有普遍意义。因此,在缺少足够多的历史数据和市场信息情况下,供应链成员用模糊集描述市场需求函数中参数的不确定性亦可求得各自的均衡最优策略,这也更加符合实际情况。
2.相对于非模糊数值,模糊数值条件下,供应链成员最优期望利润水平更高,即在模糊环境下供应链成员各自选择最优广告策略时,获得的最优期望利润大于非模糊环境下的最优利润。这为供应链成员在实际营销活动过程中,根据模糊市场需求环境,制定和选择最优策略提供了理论依据。
3.相对于模糊参数高值变化,模糊参数低值变化时,供应链成员最优期望利润曲线更加陡峭,变化速度更快,即参数低值变化对供应链成员期望利润的影响更加敏感。因此,供应链成员在预测和判断相关参数变化时,如果其是风险厌恶型,可采取与上下游市场主体信息共享、一体化策略和成本分摊等合作方式,使之更加快速、准确地预测和判断模糊参数低值变化范围,从而减少不确定性风险带来的损失。
五、结语
本文在模糊参数条件下,运用模糊截集理论和博弈理论,讨论了单个零售商和单个制造商组成的二级供应链广告纳什博弈问题,通过分析得到了供应链成员最优策略和最优期望利润,对相关参数与最优策略关系进行了分析,最后通过调整模糊参数低值和高值,对比说明了模糊参数低值与高值变化对最优期望利润的影响。研究结果表明:
第一,产品批发价格、零售价格与市场基本需求呈正相关,与价格敏感程度呈负相关,与广告活动效应无关。制造商全国性广告活动参与水平、零售商地方性广告活动参与水平与市场基本需求和其广告活动效应呈正相关,与价格敏感程度呈负相关。
第二,虽然市场基本需求和价格敏感程度参数是模糊的,但决策结果是清晰的,非模糊数值是模糊数值的一种特殊情况,模糊数值更具有普遍意义。并且模糊环境下供应链成员各自选择最优广告策略时,获得的最优期望利润大于非模糊环境下的最优利润。
第三,模糊参数低值变化对供应链成员的期望利润的影响比高值变化更加敏感,供应链决策者可根据自己的风险偏好类型选择合适的策略,使之更加准确、快速地预测和判断模糊参数低值和高值变化情况,降低不确定性风险和减少不必要的损失。
然而,以上结论是在需求函数简化的条件下讨论的,如果改变需求函数,其对最优广告策略产生那些影响,实际的广告活动中,双方掌握的市场需求信息是不对称的,此时双方广告最优策略和最优期望利润将会怎么变化,以及多个零售商或多个制造商之间的广告博弈问题,将是下一步研究的主要内容。
[1]Alaei S,Alaei R,Salimi P.A game theoretical study ofcooperativeadvertisinginasingle-manufactur⁃er-two-retailers supply chain[J].The International Jour⁃nal of Advanced Manufacturing Technology,2014,74(1):101-111.
[2]Huang Z,Li S X.Co-op advertising models in manu⁃facturer–retailer supply chains:A game theory approach[J].European Journal of Operational Research,2001,135(3):527-544.
[3]Yue J,Austin J,Wang M C,et al.Coordination of cooperative advertising in a two-level supply chain when manufacturer offers discount[J].European Journal of Op⁃erational Research,2006,168(1):65-85.
[4]Szmerekovsky J G,Zhang J.Pricing and two-tier ad⁃vertising with one manufacturer and one retailer[J].Euro⁃pean Journal of Operational Research,2009,192(3):904-917.
[5]Jinxing Xie,Alexandre Neyret.Co-op advertising and pricing models in manufacturer–retailer supply chains[J].Computers&Industrial Engineering,2009,56:1375-1385.
[6]Xieab J.,&Wei,J.C.Coordinating advertising and pric⁃ing in a manufacturer–retailer channel[J].European Journal of Operational Research,2009,197(2):785-791.
[7]Kunter M.Coordination via cost and revenue sharing in manufacturer–retailer channels[J].European Journal of Operational Research,2012,216(2):477-486.
[8]Jørgensen S,Zaccour G.A survey of game-theoretic models of cooperative advertising[J].European Journal of Operational Research,2014,237(1):1-14.
[9]ZadehL A.Fuzzy sets[J].Information&Control,1965,8(3):338-353.
[10]Van Laarhoven P J M,Pedrycz W.A fuzzy exten⁃sion of Saaty's priority theory[J].Fuzzy Sets&Systems,1983,11(1-3):199-227.
[11]李荣钧.模糊多准则决策理论与应用[M].北京:科学出版社,2002.
[12]Liu Y K,Liu B.Expected value operator of random fuzzy variable and random fuzzy expected value models[J].International Journal of Uncertainty,Fuzziness andKnowledge-Based Systems,2011,11(2):195-215.
[13]Kunter M.Coordination via cost and revenue sharing in manufacturer–retailer channels[J].European Jour⁃nal of Operational Research,2012,216(2):477-486.
[14]Jørgensen S,Zaccour G.Equilibrium Pricing and Ad⁃vertising Strategies in a Marketing Channel[J].Journal of Optimization Theory and Applications,1999,102(1):111-125.
[15]Seyedesfahani M M,Biazaran M,Gharakhani M.A game theoretic approach to coordinate pricing and verti⁃cal co-op advertising in manufacturer–retailer supply chains[J].European Journal of Operational Research,2011,211(2):263-273.
[16]Nash J F.Equilibrium Points in n-Person Games[J].Proceedings of the National Academy of Sciences of the United States of America,1950,36(1):48.
[17]Arrow K J,Debreu G.Existence of an Equilibrium for a Competitive Economy[J].Econometrica,1954,22(3):265-290.

