基于安全博弈的SDN数据包抽检策略

张伟丽， 王兴伟， 张 爽， 黄 敏

(1.东北大学 软件学院 辽宁 沈阳 110000； 2.东北大学 信息科学与工程学院 辽宁 沈阳 110000)

0 引言

软件定义网络(software defined networking，SDN)是一种新兴的网络架构，其最大的特点在于网络集中控制和可编程性,使得网络的自动化管理和控制能力获得空前提升，能够有效地解决传统网络所面临的资源规模扩展受限、组网灵活性差、难以快速满足业务需求等问题.SDN在推动网络创新的同时，其脆弱性也受到了学术界和工业界的广泛关注.关于SDN在安全方面的优缺点被分类阐述[1-3]，针对一些特定安全问题的解决方案也被不断提出.文献[4]对交换机进行了扩展，缓解了数据层和控制层之间固有的通信瓶颈，并帮助控制层进行自动化的网络管理.文献[5]给出了一种基于控制器的健壮网络架构，使得数据平面具备从多链路故障中快速恢复的能力.文献[6]面向OpenFlow构建了一个安全实施内核，并对NOX控制器进行了扩展，引入了角色身份认证与安全限制机制，但主要是用于解决应用下发流规则时可能产生的冲突问题，以确保高优先级规则能够加入到交换机中.

SDN基于流的控制粒度使得控制器对数据流的内部信息(如每个数据流包含哪些数据包、数据包的内容)并不了解，这使得网络很容易被蠕虫、特洛伊木马、垃圾信息等攻击，故为了保证SDN的安全性，对数据包进行检测是必要的和重要的.显然，由于安全资源有限等实际条件约束，检测网络中所有的数据包是不可能的，只能选取一部分数据包进行检测[7].为了尽可能保证网络安全，需要考虑检测哪些数据包以使其对上述攻击的检测成功率最高.本文设计并仿真实现了一种基于安全博弈的SDN数据包抽检策略，以优化SDN数据包抽检问题中的网络安全资源配置.

安全博弈理论为有限安全资源的最优配置提供了恰当的数学模型.它将攻击者与防御者之间的博弈建模成Stackelberg博弈.其中攻击者充当追随者的角色，防御者充当领导者的角色[8].近年以来，关于安全博弈理论的研究取得了很好的进展，并已成功应用在保护各种关键公共基础设施上，如空中警察的调度分配[9]、协助警方制定地铁巡逻日程[10]、规划机场检查点的设置以及警犬巡逻路线[11]等.计算机网络安全的资源配置是一个新兴的应用方向，安全博弈论为优化网络安全资源配置提供了有力的理论基础.

1 SDN数据包抽检问题安全博弈模型

在SDN数据包抽检问题中，攻击者的行为可以看作是从一台受控的网络设备(称为源)向一台或多台网络设备(称为目的)发送恶意包；防御者的目标是通过抽检一些数据包以识别出攻击者进而阻止攻击.根据上述问题背景提出以下假设：

假设1在有限的安全资源约束下，防御者只能检测经过网络中h段链路的数据包.

假设2攻击者总是追求收益最大化.例如，攻击者倾向于攻击能带给他最大收益的网络设备.

对防御者有限的安全资源量化，将假设1作为防御者进行数据包抽检的前提条件.在攻防博弈过程中，攻击者和防御者都希望通过最优的策略来最大化自己的收益，所以假设2合理.在上述合理假设的基础上，将SDN数据包抽检问题建模成攻防双方参与的零和安全博弈，通过对上述安全博弈模型求解，得到防御者的均衡策略，也就是SDN数据包抽检策略.

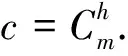
每个目的节点Nt有相应的收益值φ(Nt)，如果攻击者发送的数据包成功到达目的节点Nt，没有被防御者抽检到则认为攻击成功，此时攻击者的收益为φ(Nt)；否则为0.相应的，此时防御者的收益为-φ(Nt)；否则防御者收益为0.Xi与Aj的交集用zij来表示，若Xi与Aj交集为空，则zij=0；否则zij=1.对于策略组合〈χ,ζ〉，攻击者的期望收益表示为

(1)

防御者的期望收益表示为

(2)

2 网络节点收益值量化

当攻击者成功攻击节点Nt时，其可获得的收益即为节点Nt所对应的收益值φ(Nt).而攻击者倾向于攻击网络中的重要节点以对网络造成更大的伤害，故根据网络节点重要性量化分析网络节点收益值，对较重要的网络节点赋予较高的收益值.网络中的节点分为交换机节点Sk∈S,S⊂N和主机节点Hk∈H,H⊂N.对于保证网络正常工作来说，交换机节点(交换设备)要比主机节点(终端设备)更为重要，同时，网络中不同交换机的重要性不同，如核心交换机比边缘交换机重要；不同主机则没有区别.综上所述，提出定理1和定理2.

定理1交换机节点的重要性高于主机节点.

定理2各交换机节点重要性可能不同，各主机节点重要性相同.

根据定理1对交换机节点和主机节点进行重要性等级的划分，交换机节点的重要性等级SILevel高于主机节点的重要性等级HILevel.可根据不同网络情景用具体数值来表示不同网络节点的重要性等级，如HILevel可取值为1～3，SILevel可取值为3～5.取值时注意体现它们之间的大小关系,即SILevel>HILevel.根据定理2量化分析网络节点的重要性.下面分别给出交换机节点和主机节点重要性的计算方法.在给出交换机节点重要性计算公式之前，首先同样基于网络G=(N,E)给出节点度(degree)、介数(betweenness)[12]、K核(K-shell)[13]的定义.

定义1节点Nk的度是其邻居节点的数目，表示为

(3)

定义2节点Nk的介数是网络中经过节点Nk的最短路径数与所有最短路径数的比值，表示为

(4)

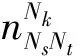
定义3由集合推导出的子网络H=(C,EC),满足C中任意节点N，其度值均大于k的最大子网络被称为K核，其中K核值等于k小于k+1的那部分节点称为K-shell，简称Ks.

分别从网络局部信息、网络全局信息、节点在网络中的位置3个方面度量交换机节点的重要性，考虑度、介数、Ks值3个指标对交换机节点重要性的综合作用，计算交换机节点Sk的重要性.

定义4交换机节点Sk的重要性Imp(Sk)等于节点度、介数、Ks值3者平方和的算术平方根.

(5)

其中:D(Sk)表示Sk的度，B(Sk)表示Sk的介数，K(Sk)表示Sk的Ks值.

根据不同的网络情景为主机节点Hk的重要性Imp(Hk)赋值.注意保证所有主机节点的重要性取值相等即可.下面给出节点收益值的定义.

定义5节点Nk的收益值φ(Nk)等于其重要性等级与重要性的乘积.表示为

φ(Nk)=ILevel·Imp(Nk),

(6)

其中:ILevel表示节点Nk的重要性等级，Imp(Nk)表示节点Nk的重要性.

3 SDN数据包抽检问题安全博弈模型求解

文献[8]证明了在双人零和Stackelberg博弈中，领导者的均衡策略就是其minimax策略(最小化对手的最大期望收益).Minimax策略是双人零和博弈中参与者很自然的一种选择.文献[14]指出在双人零和博弈中，无论哪个参与者先行选择策略，当双方都选择minimax策略时达到nash均衡.此时的解是稳定的.综上所述，求解双人零和安全博弈就是计算攻防双方的minimax策略.

对于纯策略集〈X，A〉，防御者的均衡策略χ*满足以下2个条件：

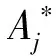
求解SDN数据包抽检问题安全博弈模型中防御者均衡策略的具体步骤如下：

1) 构建防御者纯策略集X，X为防御者所有可能的抽检链路集合，即任意h段链路的组合；

2) 构建攻击者纯策略集A，A为攻击者所有可能的攻击路径，即任意两节点间路径的集合；

3) 根据攻防双方纯策略集〈X，A〉计算防御者的均衡策略χ*，即

maxUx(χ*,Aj*)， s.t.Ua(χ*,Aj*)≥Ua(χ*,Ap)∀Ap∈A.

(7)

4 仿真分析

为了验证上述模型及方法的有效性，在基于Floodlight+Mininet的仿真环境下，分别采用5种拓扑结构和3种攻击策略交叉进行15组仿真，每组仿真重复进行10次，与随机抽检对比，评价基于安全博弈的SDN数据包抽检策略对攻击的检测成功率及攻击者的收益.其中拓扑结构如表1所示，攻击者的攻击策略如表2所示.

对每组仿真得到的10次结果取平均值.在不同拓扑结构与攻击策略的组合下，对比基于安全博弈的SDN数据包抽检策略与随机抽检策略，防御者对攻击的检测成功率及攻击者的收益如表3所示.本文给出的具体收益数值都是以金融货币为单位的，可用美元表示。

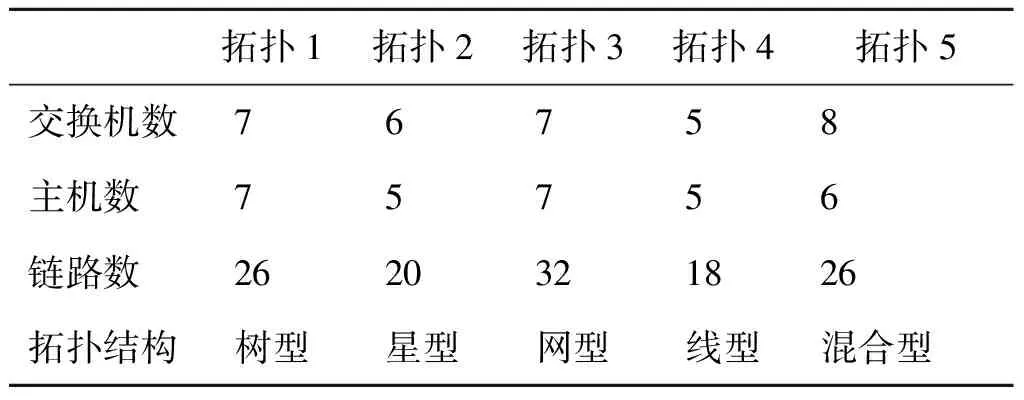
表1 拓扑结构

表2 攻击策略

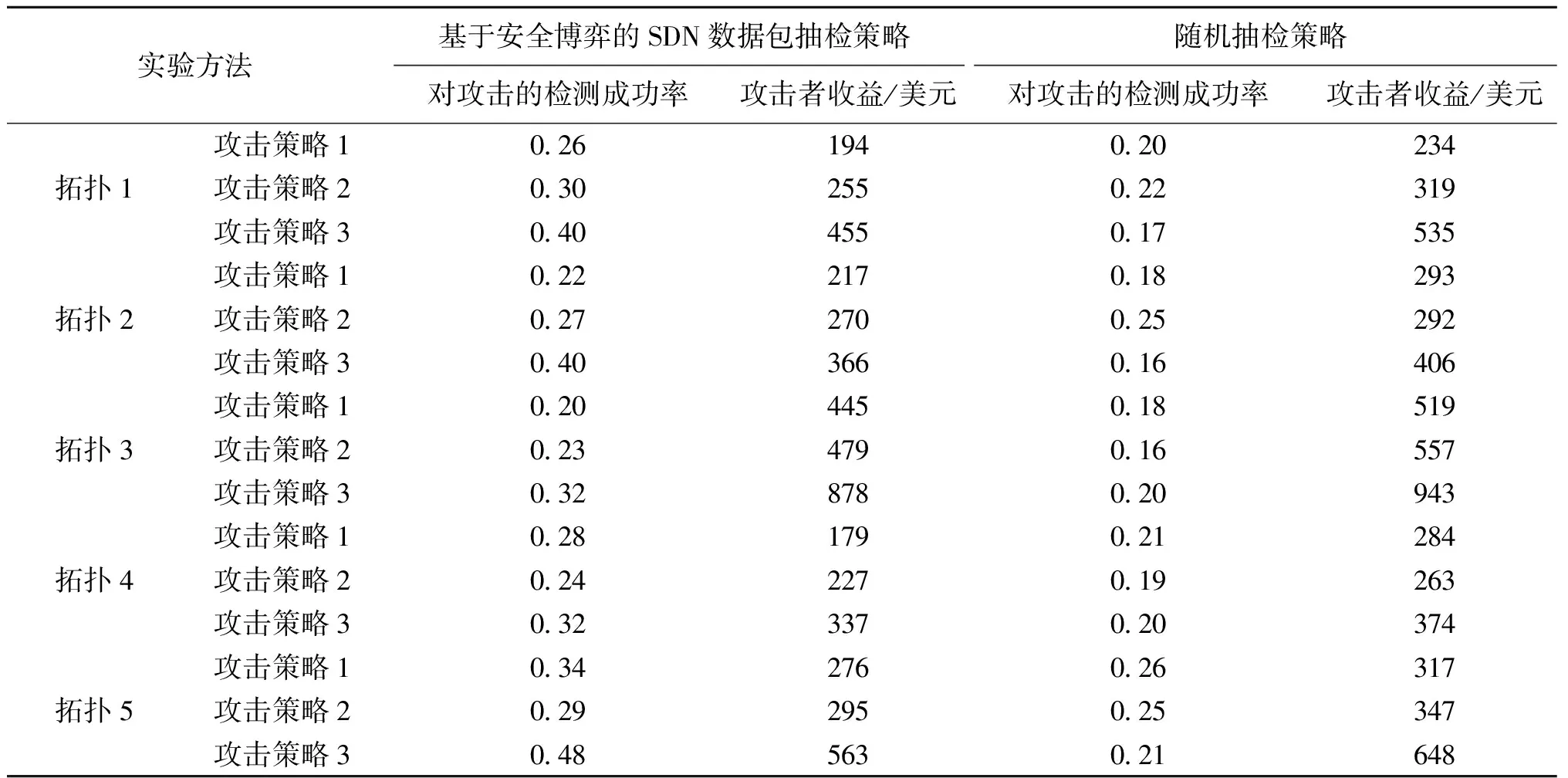
表3 两种抽检策略对攻击的成功检测率及攻击者的收益

由仿真结果表明，对比随机抽检策略，基于安全博弈的SDN数据包抽检策略对攻击的检测成功率更高；攻击者所获得的收益更低.同时，通过观察防御者采用基于安全博弈的SDN数据包抽检策略进行抽检，而攻击者分别采用3种攻击策略进行攻击时的仿真结果，我们发现，当攻击者选择攻击网络中的重要节点(即采用攻击策略3)时，防御者对攻击的检测成功率最高；当攻击者通过观察防御者的策略以做出最优回应(即采用攻击策略1)时，攻击者的收益最低.原因是基于安全博弈的SDN数据包抽检策略倾向于保护网络中的重要节点以尽可能保证网络安全.

综上所述，基于安全博弈的SDN数据包抽检策略是有效的.

5 总结

SDN基于流的控制粒度导致其很容易遭到蠕虫、特洛伊木马、垃圾信息等攻击，故在SDN中对数据包进行检测是必要的和重要的.为了优化SDN数据包抽检问题中的网络安全资源配置，本文提出SDN数据包抽检问题安全博弈模型及网络节点收益值量化方法，防御者的均衡策略即为有限安全资源约束下最优的SDN数据包抽检策略.仿真结果表明，基于安全博弈的SDN数据包抽检策略是有效的.考虑到攻击者类型是具有多样性的，今后的工作重点是将SDN数据包抽检问题安全博弈模型扩展为贝叶斯形式.

[1] KREUTZ D, RAMOS F M V, VERISSIMO P. Towards secure and dependable software-defined networks[C]//ACM SIGCOMM Workshop on Hot Topics in Software Defined Networking. Hong Kong, 2013:55-60.

[2] DABBAGH M, HAMDAOUI B, GUIZANI M, et al. Software-defined networking security: pros and cons [J]. IEEE communications magazine, 2015, 53(6):73-79.

[3] AKHUNZADA A, AHMED E, GANI A, et al. Securing software defined networks: taxonomy, requirements, and open issues [J].Communications magazine, 2015, 53(4):36-44.

[4] SHIN S,YEGNESWARAN V, PORRAS P, et al. Avant-guard: scalable and vigilant switch flow management in software-defined networks[C]//Proceedings of the 2013 ACM SIGSAC Conference on Computer & Communications Security. Berlin, 2013:413-424.

[5] KIM H, SCHLANSKER M, SANTOS J R, et al. Coronet: fault tolerance for software defined networks[C]//Proceedings of the 20th IEEE International Conference on Network Protocols (ICNP). Austin, 2012:1-2.

[6] PORRAS P, SHIN S, YEGNESWARAN V, et al. A security enforcement kernel for open flow networks[C]// Proceedings of the ACM HotSDN. Helsinki, 2012:121-126.

[7] HU Z, WANG M, YAN X, et al. A comprehensive security architecture for SDN[C]// International Conference on Intelligence in Next Generation Networks. Paris, 2015:30-37.

[8] CONITZER V, SANDHOLM T. Computing the optimal strategy to commit to[C]//ACM Conference on Electronic Commerce. Ann Arbor, 2006:82-90.

[9] TSAI J,RATHI S,KIEKINTVELD C, et al. IRIS: a tool for strategic security allocation in transportation network[C]//Proceedings of the 8th International Conference on Autonomous Agents and Multiagent Systems. Budapest, 2009:37-44.

[10] YIN Z Y, JIANG A X, TAMBE M, et al. Trusts: scheduling randomized patrols for fare inspection in transit systems using game theory [J].AI magazine, 2012, 33(4):59-72.

[11] PITA J,JAIN M, ORDEZ F, et al. Using game theory for Los Angeles airport security[J].AI magazine, 2009,30(1): 43-57.

[12] FREEMAN L C.A set of measures of centrality based on betweenness [J].Sociometry, 1977, 40(1): 35-41.

[13] KITSAK M,GALLOS L K,HAVLIN S,et al. Identifying influential spreaders in complex networks [J].Nature physics,2010,6(11):888-893.

[14] NEUMANN J V. Zur theorie der gesellschaftsspiele [J].Mathematische annalen, 1928, 100(1): 295-320.