基于噪声可见性函数的SAR图像增强快速算法
朱逸飞,杨 国,王 强,吴 文
(南京理工大学 近程高速目标探测技术国防重点学科实验室,南京 210094)
0 引言
合成孔径雷达SAR(synthetic aperture radar)是一种高分辨率成像雷达,具有全天时、全天候、穿透性强等特点,广泛应用于军事和民用领域。但由于战场环境复杂、大气衰减、硬件设备干扰等原因,SAR成像结果会存在整体灰度分布低且集中、图像对比度低、含有噪声等问题,造成目标不清晰、图像模糊,影响图像识别效果,因此需要对SAR图像进行增强[1]。目前国内外利用数据处理的方法提高SAR图像质量主要分为两类[2]:一是在成像阶段利用系统回波数据,通过超分辨成像算法获得高分辨率的SAR图像,即SAR的超分辨成像方法;二是在成像后的图像数据基础上进行图像质量提高的处理。其中后者是本文的研究内容,典型算法如Kuan算法、Lee算法、双边滤波算法、偏微分算法等,这些算法能够滤除部分噪声并保留细节边缘和目标特征[3]。但是,典型的SAR图像增强算法复杂度较高,面对高分辨率图像时,需要的计算时间较长,在目标识别、跟踪及灾难评估等对实时性要求较高的领域,无法满足系统要求。
与中央处理器CPU(central processing unit)不同,图形处理器GPU(graphic processing unit)专为密集型、高度并行化的计算而设计,其中用于数据处理的晶体管数量远远大于缓存和逻辑控制部分,这使得GPU更适合处理无逻辑关系数据的并行运算[4]。2007年,NVIDIA公司推出通用并行计算架构CUDA(compute unified device architecture),目的是将GPU作为并行计算设备,进行通用并行计算[5]。CUDA为开发者提供了硬件的直接访问接口,可以方便地写出在GPU上执行的程序,而不用像过去的GPGPU架构,如OpenGL等,将计算映射到图形API中,大大降低了开发门槛和难度。自推出后,CUDA被广泛应用于计算机可视化、音视频编解码、流体力学模拟等领域,都能获得较高的加速比,有着良好的应用前景[6]。
本文提出一种基于噪声可见性函数的SAR图像增强快速算法及其基于GPU的并行化实现方法。该算法运用图像分层理论,分离SAR图像细节与噪声,在对图像细节层进行处理时,结合人眼视觉特性,引入噪声可见性函数,控制细节层增益系数,实现图像增强。在提高图像质量、增强图像细节的同时,充分运用GPU的并行计算特点,具有较高的实时性。
1 基于图像分层的增强算法
为了抑制图像噪声、增强图像细节、提高图像识别效果,Branchitta F等人提出了图像分层理论[7]。其基本思想为:首先,选择一种分层滤波器对原始输入图像进行处理,抹平图像细节和微小波动,得到图像基本层和细节层;其次,分别对图像基本层和细节层进行处理,因为基本层中不包含图像细节信息,所以处理过程中不必考虑细节损失问题,重点在于图像对比度的调整;由于细节层不仅包含原始图像的细节信息,还有噪声的存在,因此需要对细节层进行噪声抑制和细节增强;最后,将处理后的基本层和细节层融合并调整显示范围,得到输出图像。
研究基于图像分层的增强算法,其重点在于分层滤波器、基本层图像处理方法和细节层图像增强方法的选择。本文采用双边滤波作为分层滤波器,对SAR图像进行双边滤波,得到抹平图像细节和微小波动后的基本层,并与原图像相减,得到包含细节信息和大量噪声的细节层;对基本层采用γ<1的伽马变换;通过噪声可见性函数控制细节层增益系数。算法框架如图1所示。
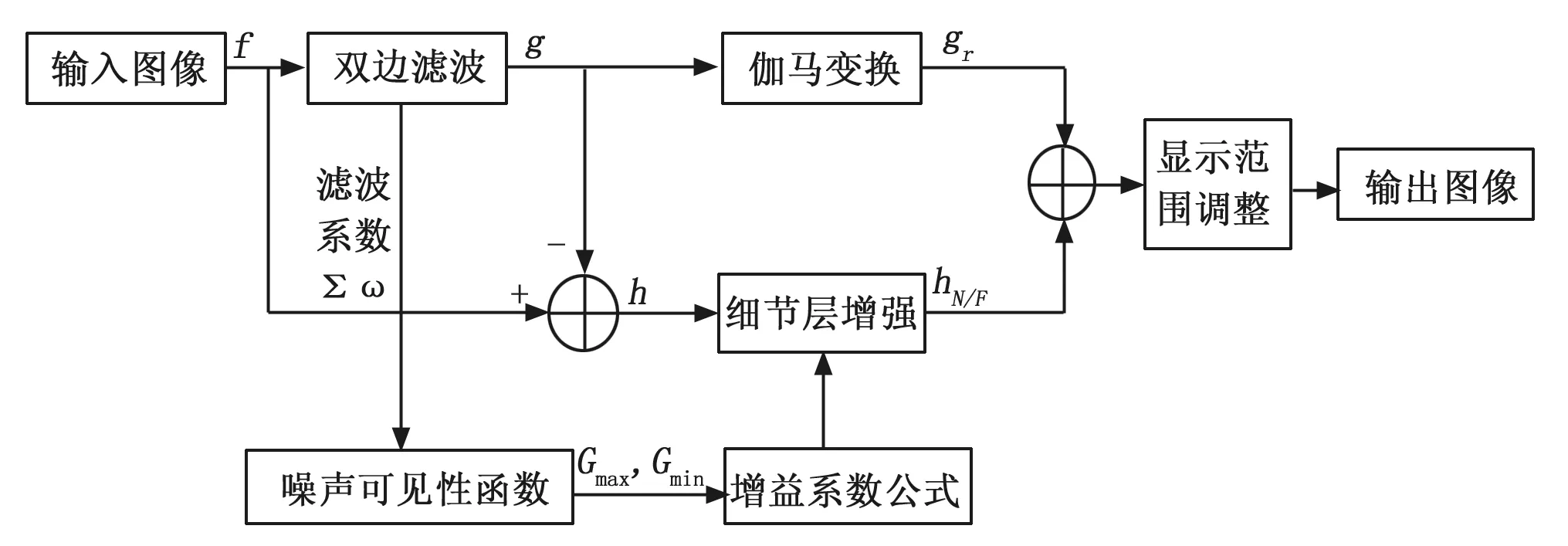
图1 基于图像分层的增强算法框架
双边滤波(Bilateralfilter)结合空域信息和灰度相似性,对图像进行基于空间分布的高斯滤波,是一种非线性的滤波方法。邻域内离中心像素较远的像素占有的权重较小,不会对中心像素的值造成太大影响,这样有利于图像细节边缘像素值的保存,达到保边去噪的目的。
设f(x,y)为原图像,g(x,y)为原图像经双边滤波后的结果,即基本层,其表达式为:
(1)
式中,Sx,y表示以像素(x,y)为中心,半宽为N的邻域,ω(i,j)为两部分系数的乘积:
ω(i,j)=ωs(i,j)ωr(i,j)
(2)
式中,ωs(i,j)为空域滤波器系数,ωr(i,j)为值域滤波器系数:
(3)
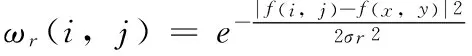
(4)
对基本层g(x,y)采用γ<1的伽马变换,拉伸图像灰度范围,提高对比度。伽马变换,也叫做幂律变换,是一种非线性的灰度拉伸变换。设变换后的基本层为gγ(x,y),变换形式为:
gγ(x,y)=C*g(x,y)γ
(5)
式中,γ为变换系数,C为控制像素变化范围的常数。
2 基于NVF的细节层增强
在研究水印估计问题时,S.Voloshnovskiy等人提出了噪声可见性函数NVF(noise visibility function)[8-9]:
(6)
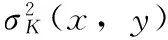
归一化处理后,式(6)变为:
(7)
式中,θ为常数,m(x,y)为噪声掩膜函数,与图像的局部方差有关,可用于衡量图像细节。
由式(7)可以看出,NVF(x,y)可以表示图像中各像素点对噪声的敏感程度,与图像局部能量成反比。越是平坦的区域,m(x,y)越小,NVF(x,y)越接近1,图像在该像素处较为敏感,噪声对人眼刺激较大,视觉效果降低;越是变化剧烈的区域,m(x,y)越大,NVF(x,y)越接近0,图像在该像素处允许较大的噪声,其对图像视觉效果的影响不明显,噪声表现出低可见性,不易被察觉。
将原图像f(x,y)与基本层g(x,y)相减得到细节层图像h(x,y)。h(x,y)中包含了原图像中的细节信息,必须进行保留或增强,但细节层中又不可避免地存在原图像中的大部分噪声。因此,在对细节层进行处理时,不能直接简单地放大,这会造成平坦区域噪声的过度放大。
增强细节层图像时,通过NVF区分图像的平坦与变化剧烈的区域,对不同的区域采用不同的增益系数。设细节层像素点(x,y)的增益系数为G(x,y),对于平坦区域的像素点,NVF趋近于1,G(x,y)需要取较小值,避免噪声被增强;对于变化剧烈的区域,NVF趋近于0,G(x,y)可以取较大值,在增强细节时不用考虑噪声的问题。设Gmax为G(x,y)的最大值,Gmin为G(x,y)的最小值,构造增益系数公式如下:
G(x,y)=Gmin+(1-NVF(x,y))(Gmax-Gmin)
(8)
(9)
且有:
m(x,y)=k(x,y)-1-1
(10)
因为k(x,y)∈[0,1],无需调整范围,所以取θ=1。由式(7)、式(8)和式(10)可得:
G(x,y)=Gmin+(1-k(x,y))(Gmax-Gmin)
(11)
增强后的细节层hNVF(x,y)可表示为:
hNVF(x,y)=h(x,y)·G(x,y)
(12)
3 基于CUDA的图像增强算法实现
3.1 CUDA编程模型
GPU拥有强大的并行计算能力,但早期的GPU编程存在很多困难,如图形API、交互接口复杂等,这些都限制了GPU在通用计算上的发展[10]。CUDA的出现解决了这一问题,其包含一整套软硬件体系,支持通用并行计算。由于CUDA采用类C语言进行开发,具有高性能计算指令开发能力,开发者能够在GPU强大的并行计算能力基础上建立更高效率的密集数据计算方案。
一个完整的CUDA程序包含在CPU(主机端,host)中执行的部分和在GPU(设备端,device)中执行的部分。如图2所示,主机端负责数据的输入输出、内存分配、主机与设备间的数据传输;而在设备端中运行的核函数(kernel)承担着并行计算的任务[11]。由于CPU对显存中的数据进行存取时只能通过PCIExpress接口,其理论带宽为双向各4GB/s,速度较慢,若频繁地进行存取显存的操作会降低GPU计算效率[12]。
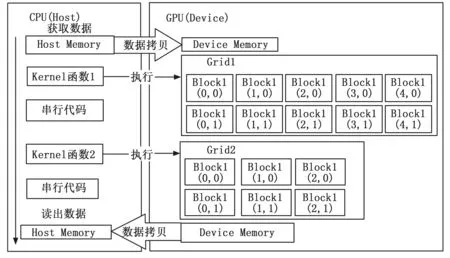
图2 CUDA编程模型
在并行线程总数确定的情况下,为了有效利用GPU的计算资源,需要对核函数进行合理的线程配置,根据GPU规格和需要计算的数据规模,合理地设定线程块Block的数量和每个线程块中线程Thread的数量。每个线程块中线程数量应为该GPU的warp大小的整数倍[13]。warp为最小单指令多线程执行单元,以32个线程为一组,并行创建、调度和执行[14],考虑存储器大小的限制,本文设定每个线程块中线程数量为256,并根据不同的图像大小划分线程块数量。
3.2 并行化图像增强算法实现
上文中图像增强算法复杂度较高,对于高分辨率图像而言,串行实现方法实时性较低。该算法中像素点间的运算相对独立,数据依赖程度较低,具有较高的内在并行性,适合GPU并行实现。在并行化双边滤波算法的基础上[15]进行线程内的分层处理、基本层处理和基于NVF的细节层增强,并行完成各像素的全部计算过程,实现算法并行化设计。
具体流程如下:
1)获取图像数据,初始化变量,申请GPU显存空间:cudaMalloc((void**)&Rdata,(width*height*sizeof(double)));
2)完成CPU与GPU间的数据通信;
3)定义线程配置:
Dim3grid(blockx,blocky,1);
Dim3block(threadx,thready,1);
4)启动kernel函数,进行并行化双边滤波和分层,根据式(11)计算细节层增益系数,完成细节层和基本层处理以及图像融合;
5)实现图像输出,释放内存和显存空间。
4 实验结果与分析
本文将从算法效果和加速性能两方面进行实验。硬件平台:CPU为IntelCorei5 6400,4核,主频2.70GHz;GPU为NVIDIAGeForceGTX960,1024核,运行频率1.22GHz;编译环境为VisualStudio2012 和CUDA7.5。
4.1 算法效果
本次实验中,考虑视觉效果和计算复杂度,取双边滤波参数σs=40、σr=20,邻域半宽N=5,基本层伽马变换系数γ=0.5,细节层增益系数最大值Gmax=1.5,最小值Gmin=1。算法实验效果如图3所示。

图3 算法效果
图3(a)为1024×1024的原始SAR图像,对图像添加噪声以模拟SAR成像结果,结果如图3(b)所示。图3(c)为经双边滤波分层后得到的未处理的基本层,图像的细节和微小波动被抹平;图3(d)为经过伽马变换后的基本层,图像对比度得到增强;图3(e)为未处理的细节层,图像细节和噪声同时存在;图3(f)为经过增强后的细节层,可以看出,在细节增强的同时,部分噪声得到了抑制;图3(g)和图3(h)分别为本文所提算法的串行实现计算结果和并行化实现方法的计算结果,可以看到,图像对比度提高的同时,噪声得到了抑制,农田部分的纹理变得更加清晰,房屋、河流等轮廓也变得十分明显。
本文通过峰值信噪比PSNR来客观评价图像质量[16],如式(13)所示。其中m、n为图像维度,f0(i,j)表示原图像,f1(i,j)表示待评价图像。PSNR值越大,说明失真越少,图像质量越高。结果如表1所示。
(13)

表1 图像PSNR值比较
从表1可以看出,本文所提算法能够有效增强图像细节,提高目标识别能力,有较好的增强效果,并且对图像质量的改善能力优于单独的双边滤波;串行实现和并行实现不会影响算法处理效果,两者得到的图像质量是一致的。
4.2 加速性能
分别对不同尺寸的SAR图像进行加速性能测试,记录算法串行实现和并行实现的计算时间。为了减小误差,提高准确程度,取10次运算结果的平均值,计算加速比。实验结果如表2所示。
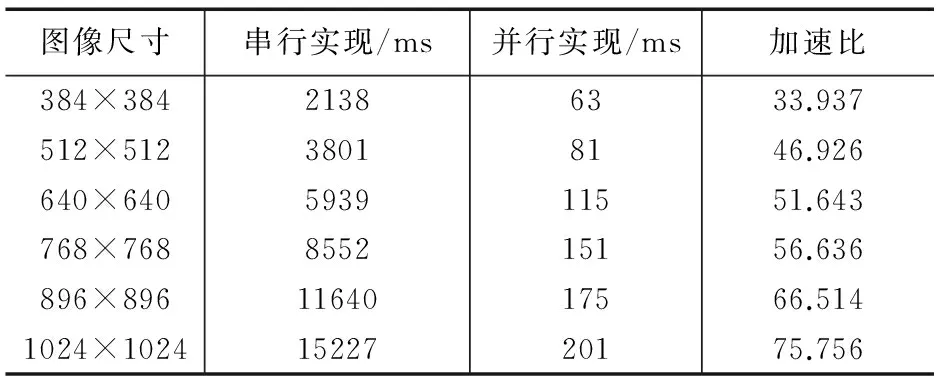
表2 计算时间对比
从表2可以看出,本文所提算法在GPU上的执行时间明显少于在CPU上的执行时间,基于CUDA的并行化实现方法具有显著的加速效果,1024×1024的图像的加速比达到75.756,这是因为本文所提算法具有较好的并行特性,能够充分利用GPU的架构和存储结构特点,并行计算各像素的处理过程;随着图像尺寸的增大,加速比逐渐提高,这是因为系统调度和数据传输需要一定的时间开销,数据规模较大时,虽然调用的线程较多,数据传输时间较长,但其在整体运行时间中所占比重较小,因此加速比较大。
5 结论
本文提出一种基于噪声可见性函数的SAR图像增强快速算法及其基于GPU的并行化实现方法。实验结果表明,该算法能够充分利用图像分层的内在并行性,实现并行加速,在有效提高图像质量,增强图像细节的同时,减少计算时间,进一步满足SAR图像增强系统实时性要求。
[1] 陈建飞,李跃华,王剑桥. 毫米波被动合成孔径成像系统[J].微波学报,2012,S1:253-256.
[2] 尹奎英. SAR图像处理及地面目标识别技术研究[D]. 西安:西安电子科技大学,2011.
[3] 陈 沫. SAR图像军事目标识别方法研究[D]. 合肥:安徽大学,2013.
[4] 张 舒. GPU高性能运算之CUDA[M]. 北京:中国水利水电出版社,2009.
[5] 姚 旺,胡 欣,刘 飞,等. 基于GPU的高性能并行计算技术[J]. 计算机测量与控制,2014,22(12):4160-4162.
[6] 宋晓丽,王 庆. 基于GPGPU的数字图像并行化预处理[J]. 计算机测量与控制,2009,17(6):1169-1171.
[7] Branchitta F,Diani M,Romagnoli M. New technique for the visualization of high dynamic range infrared images[J]. Optical Engineering,2009,48(9):6401.
[8] Voloshynovskiy S,Pereira S,Iquise V,et al. Attack modelling: towards a second generation watermarking benchmark[J]. Signal Processing,2001,81(6):1177-1214.
[9] 汤代佳,尚东方. 基于噪声可见性函数的交通流量异常预警算法[J]. 上海电机学院学报,2012,15(6):386-389.
[10] 班阳阳,张劲东,陈家瑞,等. 后向投影成像算法的 GPU 优化方法研究[J]. 雷达科学与技术,2014(6):659-665.
[11] 张绍良,闫钧华,刘 成,等. 基于CUDA的红外图像快速增强算法研究[J]. 电子设计工程,2012,20(17):153-157.
[12] Zhao C,You W,Wang Y,et al. GPU implementation for real-time hyperspectral anomaly detection[A]. IEEE International Conference on Digital Signal Processing[C]. IEEE,2015:940-943.
[13] Yiu B Y S,Tsang I K H,Yu A C H. Real-time GPU-based software beamformer designed for advanced imaging methods research[C]. Ultrasonics Symposium. IEEE,2011:1920-1923.
[14] 李大禹,胡立发,穆全全,等. CUDA架构下的液晶自适应波面数值解析[J]. 光学精密工程,2010,18(4):848-854.
[15] 曾炫杰,陈强,谭海鹏,等. 基于CUDA的加速双边滤波算法[J]. 计算机科学,2015,42(s1).
[16] 段 群,吴粉侠,刘小豫. 基于CUDA的椒盐噪声自适应中值滤波算法[J]. 航空计算技术,2013,43(2):60-63.

