水淹层评价中Rw、m、n值的确定

孙游雪，高齐明，魏玉梅，刘小璇，孔 杰

(1.油气资源与勘探技术教育部重点实验室(长江大学)，湖北 武汉 430100；2.长江大学 地球物理与石油资源学院，湖北 武汉 430100；3.中国石油集团渤海钻探有限公司 测井分公司，天津 300280)

阿尔奇公式是最早提出描述地层导电特性与孔隙度、饱和度和流体电阻率关系的模型,奠定了定量评价地层流体饱和度的基础[1].阿尔奇公式中地层水电阻率(Rw)、胶结指数(m)、饱和度指数(n)的确定是计算含水饱和度的关键.注水开发前，阿尔奇公式中胶结指数的大小仅与孔隙的几何形状有关，孔隙几何形状愈复杂，m值愈高.饱和度指数的影响因素主要包括油气的相对体积、油气在孔隙中的分布及其对岩石的润湿性、油气在孔隙中的连通情况以及其与地层水之间的表面张力等[2].注水开发后，地层孔隙空间注入了注水开发前不曾有过的流体(水、气、化学剂等)[3]，地层孔隙空间流体性质因各种因素发生了相应变化，储层特征也随着注水开发的不断深入而发生相应的变化，因而Rw、m、n值在地层条件下也处于相应的变化之中.因此，对于水淹层评价而言，Rw、m、n值随着注水开发程度的变化而发生变化，利用相对固定的Rw、m、n值则无法准确解决水淹层含油饱和度定量计算的问题.

1 地层混合液电阻率计算方法研究

地层混合液电阻率(Rw)是利用阿尔奇公式计算含油饱和度的重要参数[4].随着注水开发的不断深入，Rw在地层条件下处于不断的变化之中.为提高水淹层测井解释精度，需逐点求取地层混合液电阻率[5-6].

由水分析资料可知，由于注入水矿化度范围较大且原始地层水矿化度随井深及温度也会产生一定差异，导致目的区块混合液电阻率变化复杂，对电阻率的影响较大，且与测井响应相关性较好.因此，可以利用地层混合液电阻率与测井曲线间的相关关系，建立地层混合液电阻率的计算模型.

目的区块地层水矿化度变化复杂，对地层电性的影响较大.因此，有必要寻找地层水矿化度(或地层混合液电阻率)与泥质含量、自然电位等参数间的变化关系，从而建立地层水电阻率的计算模型.图1、图2、图3、图4分别为目的区块地层混合液电阻率、地层电阻率与自然电位交会图；地层混合液电阻率、地层电阻率与泥质含量交会图；地层混合液电阻率、地层电阻率与孔隙度交会图；地层混合液电阻率、自然电位与孔隙度交会图.由图可知，利用自然电位、孔隙度及地层电阻率可以逐点求取地层混合液电阻率.

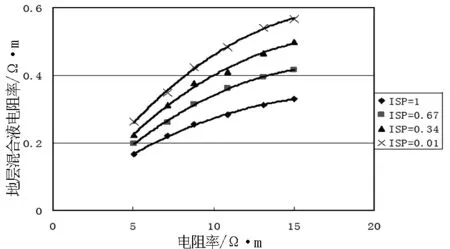
图1 地层混合液电阻率、地层电阻率与自然电位交会图Fig.1 Crossplot of mixed formation water resistivity、formation resistivity & spontaneous potential

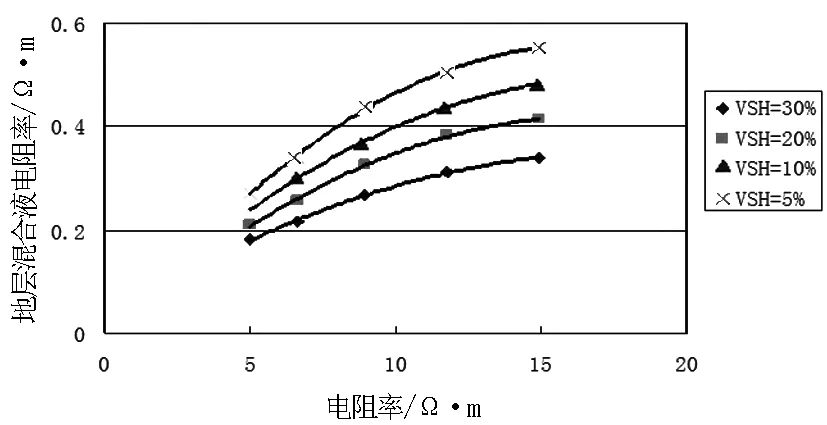
图2 地层混合液电阻率、地层电阻率与泥质含量交会图Fig.2 Crossplot of mixed formation water resistivity、formation resistivity & shale content

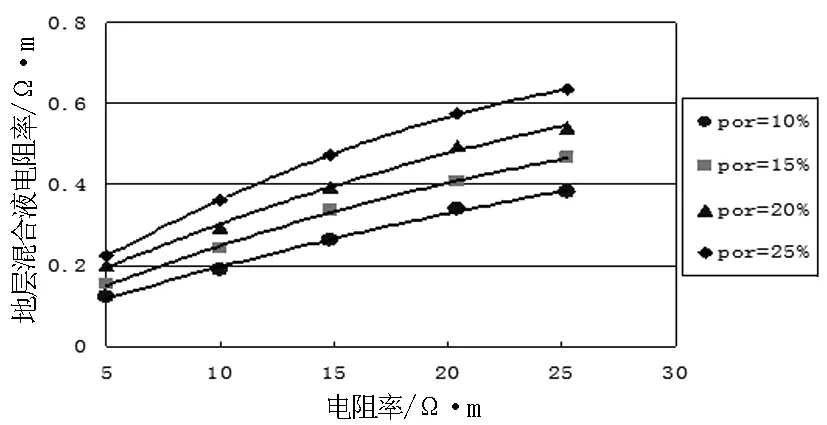
图3 地层混合液电阻率、地层电阻率与孔隙度交会图Fig.3 Crossplot of mixed formation water resistivity、formation resistivity & porosity

图4 地层混合液电阻率、自然电位与孔隙度交会图Fig.4 Crossplot of mixed formation water resistivity、spontaneous potential & porosity

2 m、n值的变化特征及其计算方法研究

饱和度指数(n)是把电阻率转换为含水饱和度的结构指数[7]，它与油、气、水在孔隙中的分布、岩石润湿性以及地层水电阻率有关[8].油田进入开发后期，油层受到水的长期冲刷，储层润湿性、油水分布发生了变化.因此，n值开发后期应与开发初期不同.

由实验资料分析可知，在水驱油模拟过程(表示油藏的注水开发过程和开发状态)，当含水饱和度较低时，岩石中的孔隙、喉道被油占据，导电能力较低，n值较小；而对强水淹层，孔隙、喉道里充满水,导电能力增强，n值较大.通过分析，虽然饱和度指数的影响因素较多，但其与地层水电阻率及地层中的泥质含量相关性较好.对同一块岩心，用不同矿化度的水进行实验，实验结果表明，泥质含量一定时，n与Rw呈反比关系，且Rw与n有良好的相关性.同时，n随着泥质含量的增加而减小(表1).

由实验分析可知，水淹层饱和度指数(n)的变化在一定程度上由地层混合液的变化及泥质分布形态的变化所引起，其对饱和指数的大小起明显作用.同时，由实验资料分析可知，胶结指数(m)与地层水电阻率和孔隙度变化有关[9].因此，绘制了饱和度指数、地层混合液电阻率与泥质含量交会图；胶结指数、地层混合液电阻率与孔隙度交会图(分别见图5、图6).由图中可以看出，m、n值的变化与地层水电阻率的变化有关，储层受到不同程度的水淹时，可引起m和n值较大变化.如果在水淹层解释中还采用原始地层水状态下的m和n值，将会给解释结果带来较大的误差.

表1 饱和度指数n随泥质含量、地层混合液电阻率变化一览表
Tab.1 Corresponding values of saturation exponent、shale content & mixed formation water resistivity

Rw/Ω·mVsh/%nRw/Ω·mVsh/%n0．501．752．0101．500．5101．641．6101．560．5201．571．1101．590．5301．460．7101．610．5501．320．5101．64

图5 饱和度指数、地层混合液电阻率与泥质含量交会图Fig.5 Crossplot of saturation exponent、mixed formation water resistivity & shale content

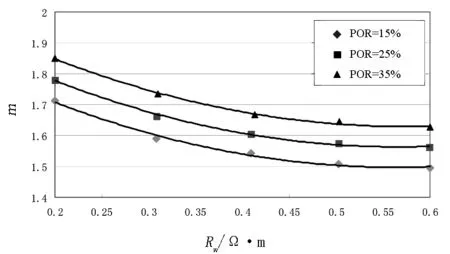
图6 胶结指数、地层混合液电阻率与孔隙度交会图Fig.6 Crossplot of cementation factor、mixed formation water resistivity & porosity

3 方法应用

综上所述，虽然Archie公式(式1)在水淹层评价中具有一定的局限性，但在利用测井资料求取地层混合液电阻率(Rw)、饱和度指数(n)和 胶结指数(m)的基础上，仍然可以利用Archie公式计算水淹层含水饱和度，进而求取其含油饱和度.

(1)

式中：Sw为含水饱和度，小数；Rt为深电阻率测井值，Ω·m；Φ为孔隙度，小数；Rw为混合液电阻率，Ω·m；a为岩性附加导电性校正系数；b为岩性润湿性附加饱和度分布不均匀系数；m为胶结指数；n为饱和度指数.

表2 解释符合率统计表
Tab.2Statisticaltableofinterpretationcoincidencerate

井名射孔井段/m解释结论试油结论符合情况G11724．2～1726．2油层油层符合G21505．9～1508．5弱水淹弱水淹符合G31663．3～1665．7弱水淹弱水淹符合G41612．9～1616．2强水淹中水淹不符合G51706．2～1709．5中水淹中水淹符合1720．0～1722．5中水淹中水淹符合G61753．1～1755．4中水淹中水淹符合G71527．5～1530．0中水淹弱水淹不符合G81724．2～1726．2强水淹强水淹符合G91689．2～1691．5中水淹中水淹符合G101691．2～1696．0强水淹强水淹符合G111884．8～1886．0强水淹强水淹符合1888．7～1892．3强水淹强水淹符合G121457．0～1461．0中水淹中水淹符合G131570．1～1574．2中水淹中水淹符合G141724．2～1726．2弱水淹弱水淹符合G151458．7～1462．0中水淹中水淹符合1473．0～1477．0中水淹中水淹符合G161542．0～1544．5弱水淹弱水淹符合1553．8～1555．0弱水淹弱水淹符合G171823．8～1829．0油层油层符合G181203．9～1313．5中水淹中水淹符合G191750．0～1762．0油层油层符合

利用建立的地层混合液电阻率(Rw)、饱和度指数(n)及 胶结指数(m)计算图版，结合目的区块解释模型，编制了相应的水淹层解释程序，对研究区块的19口井进行了处理(表2)，其中试油层23层，解释符合21层，不符合2层，解释符合率91.3%，验证了研究方法的实用性.

为进一步说明处理资料的准确性，以G6井为例进行分析说明.由试油资料可知，G6井试油井段为1 753.1～1 755.4m，日产油9.57m3，日产水17.58m3，产水率64.7%.图7为利用所研究的方法处理的G6井测井解释成果图(a=0.99，b=0.93)，由图7可知，计算饱和度指数(n)为1.15，胶结指数(m)为1.6，混合液电阻率(Rw)为0.46(Ω·m)，含水饱和度(SWP)为57.8%，残余油饱和度为30.7%，束缚水饱和度为39.04%，可动水饱和度为18.76%，可动油饱和度为11.5%，产水率为62.9%(FWP)，综合解释为中水淹层，解释结论与试油结论相符.为了说明研究方法的优越性，同时利用原始阿尔奇公式(a=0.99，b=0.93，m=1.64，n=1.266，Rw=0.65)对G6井进行了处理.由图7可以看出，其含水饱和度(SW)为67%，残余油饱和度为30.7%，束缚水饱和度为39.04%，可动水饱和度为27.96%，可动油饱和度为2.93%，产水率为81%(FW)，综合解释为强水淹层，解释结论与试油结论不符.从而进一步说明了利用建立的地层混合液电阻率(Rw)、饱和度指数(n)和 胶结指数(m)计算图版计算的含水饱和度，优于利用目的区块原始地质参数(Rw、m、n)计算的含水饱和度.

图7 G6井解释成果图Fig.7 Graph of G6 well interpretation

4 结论

本文通过分析注水开发前后，地层混合液电阻率Rw、胶结指数m、饱和度指数n变化特征，绘制了其计算图版，并进行了现场应用，应用效果良好.

(1)不同开发时期、不同测井深度应采用不同的Rw、m、n值，才能更有效的应用阿尔奇公式计算含油饱和度.

(2)利用孔隙度、地层电阻率及自然电位等参数，可以逐点计算水淹层混合液电阻率.

(3)随着水淹程度的变化，胶结指数m、饱和度指数n而不断发生变化。胶结指数m、饱和度指数n的变化与地层混合液电阻率、孔隙度、泥质含量的变化有关，可以利用混合液电阻率、孔隙度、泥质含量计算m、n值.

(4)利用建立的地层混合液电阻率(Rw)、饱和度指数(n)和 胶结指数(m)计算图版，进行了实际资料处理(处理了19口井，解释符合率91.3%)，应用效果良好.

[1]章海宁,汤天知,刘堂晏，等. 基于地层孔隙结构的饱和度评价方法[J]. 地球物理学进展,2015,30(2):710-717.

[2]邹良志.阿尔奇公式中参数的影响因素分析 [J]. 国外测井技术,2013(4):22-27.

[3]傅爱兵,王善江.含水饱和度指数n值计算方法探讨[J].测井技术，2007,31(5):437-440.

[4]陆云龙,李兴丽,吕洪志，等.混合液地层水电阻率反演在水淹层评价中的应用[J]. 测井技术,2016,40(2):190-196.

[5]袁伟,张占松,吕洪志，等.水淹层混合液地层水电阻率的计算方法[J]. 石油天然气学报,2014,36(9):78-83.

[6]王美珍,俞军.用测井资料确定大庆长垣水淹层混合液电阻率[J].大庆石油地质与开发,2007,26(2):119-122.

[7]唐文江, 甄廷江,冯春珍.浅谈阿尔奇公式中饱和度指数(n)的测定方法[J].测井技术,2005,29(4):300-388.

[8]宋延杰,姜艳娇,宋杨，等.古龙南地区低阻油层胶结指数和饱和度指数影响因素实验[J].吉林大学学报(地球科学版),2014,44(2):704-714.

[9]王建功,蔡文渊.二连地区复杂砂岩胶结指数m和系数a的研究[J].测井技术,2010,34(5):449-452.