基于Nystrom方法的水平集医学图像分割算法

王晓丹，张龙波，王 雷，刘 晨

(山东理工大学 计算机科学与技术学院，山东 淄博 255049)

1 相关研究

近年来，水平集算法已经较为成熟地应用于医学图像分割领域，这是一种有效解决曲线演化问题的数值方法，并且计算稳定，适宜任意位数空间[1].水平集的基本思想是低维到高维的映射，把低维空间上的函数通过水平集的方法转化到高维空间.文献[2]提出了著名的测地线主动轮廓模型(Geodesic Active Contour，GAC)，它允许曲线在演化过程中改变拓扑结构，分割结果与初始化曲线的拓扑形态无关.但需要对水平集函数不断初始化，代价昂贵，且演化曲线易在弱边缘处泄露，造成分割错误.

由于图像分割问题是将图像的像素进行分类，因此可以运用聚类分析优化图像分割算法.文献[3]提出基于模糊聚类水平集的图像分割方法，算法首先使用模糊C均值(fuzzy C-means clustering，FCM)聚类，得到聚类后的图像模型，再利用水平集算法进行图像分割.虽然提高了分割的精度，有效地减少了迭代次数，但FCM方法对初始化参数敏感，容易陷入局部最小值.文献[4]提出了基于核模糊聚类的变分水平集医学图像分割算法，将原始图像进行核模糊C均值聚类，然后将聚类结果带入水平集函数得到初始轮廓，最后利用一种无须重新初始化的水平集模型分割图像.核函数对噪声有很强的处理能力，但基于核方法的模糊聚类算法迭代次数多，运算时间长.除了模糊聚类，基于图论的聚类也是近年来研究的热点.文献[5]介绍并使用基于连续最大流的方法对心脏CT图像进行分割实验，最终得到左心室心机的分割结果.文献[6]将图论方法应用于脊椎骨磁共振图像的分割.文献[7]提出一种新的基于图论的分割方法，将图像中灰度相同的像素作为一类，改进加权函数的定义，将节点与区域间的空间近邻关系约束进加权函数.

针对现有的基于最小化区域扩展拟合能量的分割模型对边缘模糊、噪声强的图像迭代时间久，易产生边缘泄露的问题，本文提出一种基于Nystrom方法的水平集医学图像分割算法.

2 基于图论的图像分割

图论法要求将图像映射为一个带权的无向图，把像素当作节点，构成最小支撑树，利用最小剪切准则得到阈值从而实现图像的最优分割[8].

2.1 谱分割

谱聚类算法是将聚类问题转化为一个无向带权图的多路划分问题[9].无向图的顶点V={v1,v2,…vn}表示像素集，vi和vj之间的相似度权值Wij表示无向图的边E，将聚类问题转化为寻找最优的分割准则G(V,E)划分为子图内部相似度最大，子图之间相似度最小.经典的NCut(Normalize cut)方法常作为最优分割准则，定义图G划分的两个子图A∪B=V，A∩B=∅，代价函数为

(1)

为了实现最佳二分割，必须找到一个合适的A和B集合使代价函数最小.根据图谱理论，可以通过计算拉普拉斯矩阵的第二最小特征值对应的特征向量对图进行分割.这样就把图划分的问题转化为求解矩阵特征值和特征向量[10].本文使用高斯核函数度量像素之间的相似度

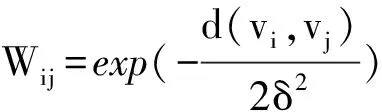
2.2 基于Nystrom方法的谱分割

谱分割在理论和应用方面效果都不错，但仍有许多不足之处.随着图像的分辨率增大，相似矩阵成幂级数增长，花费大量的存储空间和计算时间，Fowlkes[11].提出通过Nystrom采样可近似估算相似矩阵和特征向量. 设原始图像有N个像素，从中随机选取m个像素点，剩下n=N-m个像素点m≪N，构造相似矩阵W为

(2)

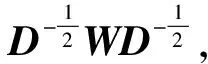
3 本文算法

本文提出的基于Nystrom方法的水平集医学图像分割算法，首先利用Nystrom谱聚类的思想，对原始图像随机采样，然后分别计算样本点之间的距离和样本点与非样本点之间的距离，并将距离转化为相似矩阵，拉普拉斯归一化处理后，得到k个特征值及对应的特征向量，再利用k-means聚类特征向量，得到聚类的图像，最后利用Li提出的水平集分割方法[13]分割图像得到结果.具体步骤为：

(1)输入原始图像，通过Nystrom算法对像素点随机采样，选取一定数量的样本点.计算样本点之间的欧式距离、样本点和非样本点之间的欧氏距离.

(2)将距离转化为相似矩阵A和B，拉普拉斯归一化相似矩阵.执行正交化和特征分解，得到k个特征值和对应的特征向量，并按降序排列.

(3)利用k-means算法聚类，得到聚类后的图像.

(4)初始化水平集函数、高斯核函数平滑图像，计算图像的曲率和梯度.

(5)基于兴趣区域设定初始轮廓和迭代次数，通过求解偏微分方程驱动水平集的演化，得到最终的分割图像.

偏微分方程PDE可以利用标准梯度下降方法最小化能量函数.能量函数公式为：

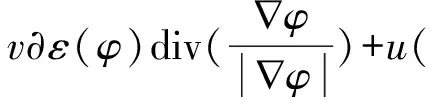
(3)

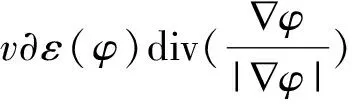
算法流程图如图1所示.

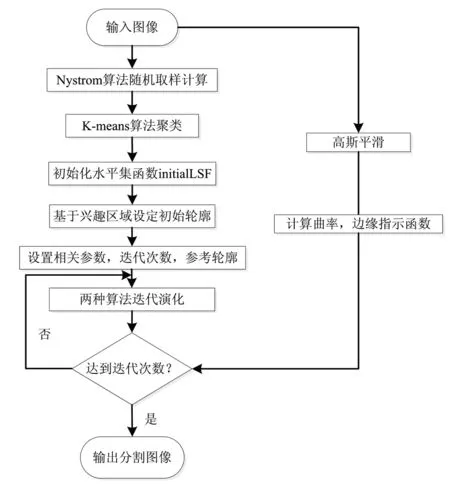
图1 本文算法流程图Fig.1 Flow chart of the algorithm in this paper

4 实验与结果分析

4.1 实验过程

为了验证本文算法，实验环境为：处理器Intel(R)Xeon(R)E5-2620，CPU2.0GHz，内存32GB，64位Windows Server2008 R2操作系统.实验从每幅图像中随机取样100个像素点，Li方法中的参数为：δ=1.0, Δt=0.1,v=0.001*255*255,λ1=λ2=1.0,u=1.0.实验根据不同的数据集，采用了不同的迭代次数，实验1和实验3选取的图像与实验2的图像相比，噪声强度相对较弱，迭代200次后，图像边界分割清晰，成功收敛到目标区域.实验2的头顶灰度图，噪声强，为避免边缘泄露问题，迭代选取400次.

实验1如图2所示，图像为103*101的血管图，实验选取13 493个像素中的100个像素进行近似估计，初始轮廓为感兴趣的不规则区域，迭代次数为200次.图2(a)为原始图像，2(b)中红色虚线为初始轮廓，2(c)中红色实线为分割参考轮廓，2(d)为两种算法迭代100次后的分割图像，2(e)为两种分割算法最终的分割结果.(d)、(e) 中黑色线为本文算法，白色线为参考轮廓，蓝色线为基于最小化区域扩展拟合能量的图像分割算法.

实验2如图3所示，图像为128*128的头顶灰度图，实验选取16384个像素中的100个像素近似估计，初始轮廓为感兴趣的不规则区域，迭代次数为400次.图3(a)为原始图像，3(b)中红色虚线为初始轮廓，3(c)中红色实线为分割参考轮廓，3(d)为两种算法迭代200次后的分割图像，3(e)为两种分割算法最终的分割结果.3(d)、3(e)中黑色线为本文算法，白色线为参考轮廓，蓝色线为基于最小化区域扩展拟合能量的图像分割算法.

实验3如图4所示，图像为128*128的酵母荧光显微图，实验选取16 384个像素中的100个像素近似估计，初始轮廓为感兴趣的不规则区域，迭代次数为200次.图4(a)为原始图像，4(b)中红色虚线为初始轮廓，4(c)中红色实线为分割参考轮廓，4(d)为两种算法迭代100次后的分割图像，4(e)为两种分割算法最终的分割结果.4(d)、4(e)中黑色线为本文算法，白色线为参考轮廓，蓝色线为基于最小化区域扩展拟合能量的图像分割算法.(注：图2-4原图是彩色，读者如需了解详情，请到本刊网站查看电子文稿)

(a)原始图像 (b)初始轮廓 (c)参考轮廓 (d)100次迭代 (e)结果对比图2 血管图分割Fig.2 The bleod vessel segmentation

(a)原始图像 (b)初始轮廓 (c)参考轮廓 (d)200次迭代 (e)结果对比图3 头顶灰度图分割Fig.3 The perietal region segmentation

(a)原始图像 (b)初始轮廓 (c)参考轮廓 (d)100次迭代 (e)结果对比图4 酵母荧光显微图分割Fig.4 The yeast micrograph segmentation

4.2 实验结果分析

从图2(e)、图3(e)、图4(e)分割结果来看，本文算法能够快速精确地收敛到目标区域，克服了基于最小化区域拟合扩展能量的图像分割算法对于像素灰度相近的图像分割效果不理想，易产生边界泄露的问题.

为了更好的分析实验结果，本文从算法分割时间和结果图像与参考图像的相似度Dice两方面进行评价，见表1、表2.算法分割时间以s为单位.

表1 分割时间比较
Tab.1 Comparision of the segmentation time s

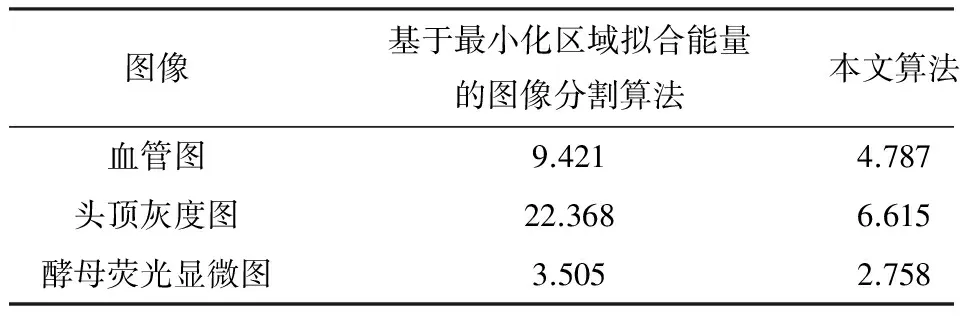
图像基于最小化区域拟合能量的图像分割算法本文算法血管图9．4214．787头顶灰度图22．3686．615酵母荧光显微图3．5052．758

表2 Dice相似度比较
Tab.2 Dice similarity comparison

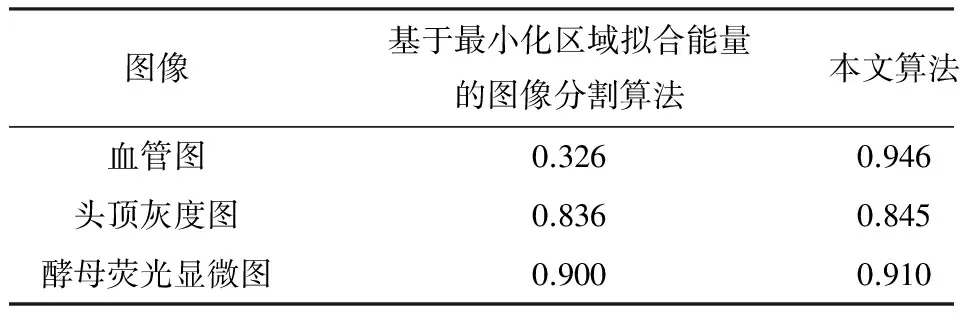
图像基于最小化区域拟合能量的图像分割算法本文算法血管图0．3260．946头顶灰度图0．8360．845酵母荧光显微图0．9000．910

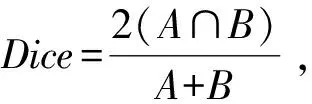
5 结束语

本文针对现有基于最小化扩展拟合能量的图像分割方法，对于图像像素灰度值相近时，分割效果不明显，在弱边缘处易产生边界泄露的现象，提出了基于Nystrom方法的水平集医学图像分割算法.通过理论分析和相关实验，证明该方法能够快速精确地收敛到目标区域，在相同的迭代次数中，本文方法能更快分割图像，并能保证较高的相似度.

[1]钱芸,张英杰.水平集的图像分割方法综述[J]. 中国图象图形学报,2008(1):7-13.

[2]CASELLES V, KIMMEL R, SAPIRO G. Geodesic Active Contours[C]// International Conference on Computer Vision. IEEE Computer Society, 1997:694.

[3]吴杰,朱家明,陈静. 基于模糊聚类水平集的医学图像分割方法[J]. 计算机科学, 2015(S2):155-159.

[4]刘雅婧,宋余庆,廖定安,等. 基于核模糊聚类的变分水平集医学图像分割方法[J]. 计算机应用研究,2013, 30(11):3 510-3 513.

[5]郭元丁. 基于图论的心脏CT图像分割的研究[D]. 杭州：浙江大学,2016.

[6]CARBALLIDO-GAMIO J, BELONGIE S J, MAJUMDAR S. Normalized cuts for spinal MRI segmentation[C]// CARS 2002 Computer Assisted Radiology and Surgery. Springer Berlin Heidelberg, 2002:1 054-1 054.

[7]刘锁兰,王江涛,王建国,等. 一种新的基于图论聚类的分割算法[J]. 计算机科学,2008,35(9):245-247.

[8]闫成新,桑农,张天序. 基于图论的图像分割研究进展[J]. 计算机工程与应用, 2006, 42(5):11-14.

[9]张洪刚,陈光,郭军. 图像处理与识别[M]. 北京：人民邮电出版社,2006.

[10]印世乐,曾志勇. 一种改进的Nystrom谱聚类图像分割算法[J]. 计算机与现代化,2014(4):20-23.

[11]FOWLKES C, BELONGIE S, FAN C, et al. Spectral grouping using the Nystrom method[J]. Pattern Analysis & Machine Intelligence IEEE Transactions on, 2004, 26(2):214-225.

[12]陈应良,王士同,钱蓉. 基于Nystrom方法的图像谱分割算法的聚类改进[J]. 计算机工程与设计,2008,29(13):3 399-3 401.

[13]LI C, KAO C Y, GORE J C, et al. Minimization of region-scalable fitting energy for image segmentation[J]. IEEE Transactionson Image Processing, 2008, 17(10):1 940-1 949.