形态参数下地表采动裂缝三维建模及可视化方法
戴华阳,王 祥,李 军,郭俊廷,阎跃观
(1. 中国矿业大学(北京)地球科学与测绘工程学院,北京 100083; 2. 中国矿业大学(北京)煤炭资源与安全开采国家重点实验室,北京 100083)
煤炭开采在给人们带来巨大经济效益的同时,也给环境带来若干负面影响,其中突出的问题是开采引起的大量地表采动裂缝[1]。地表采动裂缝作为一种表生的地质灾害现象,在世界许多国家普遍存在,并已成为一种主要的区域性地质灾害现象,它对各类工程建筑、交通设施、城市生命线工程及土地资源造成了灾难性的直接破坏,并有可能引发严重的生态环境问题[2]。深入研究采动引起的地表裂缝并减缓和防治地裂缝灾害是资源安全开采和环境保护的重要内容。当前较为常用的地裂缝记录和发布的方式是采用二维平面图和剖面图,但该方法会导致地表采动裂缝的大量空间信息丢失,同时加大理解和判别裂缝空间信息的难度[3]。因此,亟须研究一种合理、实用的地表采动裂缝三维建模及可视化方法,以实现对多类复杂采动裂缝结构、形态、空间关系等的直观认知。
随着近年来地理信息技术的不断发展,三维建模及可视化技术已经越来越受到青睐,地物地貌的三维模型不仅具有虚拟现实的真实感,而且能提供真实、准确的三维地理坐标,便于进行空间分析和空间运算。目前三维建模的研究主要针对两大类对象:人工构筑物和自然地貌。人工构筑物包括建筑、水塔、桥梁、管线等由人建造或构建的物体,由于此类地物形状相对规则,学术界和工业界已经开发多种软件,可以通过基本建模要素的组合实现。张晖等应用CityEngine利用建筑物的基底投影数据及内部房间分布矢量化数据生成建筑外立面三维模型[4];张帆等应用Creator实现大范围的虚拟城市三维建模[5];尹晖等利用Google SketchUp实现了对输电杆塔、绝缘子及金具的建模[6]。与人工构筑物不同,自然地貌或地质体等的三维建模方法较多,主要分为3类:基于面表示的数据模型、基于体表示的数据模型和混合数据模型。不少学者在这方面开展了研究工作,如程朋根等研究了以似三棱柱体为体元的三维数据模型表达地质体[7];颜辉武采用Kriging插值方法建立水文地质层的三维模型,并利用体绘制技术进行可视化表达[8]。虽然地理三维建模取得了很大进展,但上述方法和软件主要面向建筑物、管道、地质体等地物地貌,若将其直接用于因矿物开采导致的地表裂缝的三维建模,会存在以下问题:①裂缝相对自然地表属于微观地貌特征,若要详尽表达裂缝的几何形态需采集大量的裂缝地貌特征点,野外测绘工作量非常大;②依据开采沉陷规律,地表采动裂缝的形态具有典型的规律,而由高程测量点直接构建TIN模型反映的裂缝形态和分布往往不能准确展现其真实规律;③直接三维建模可视化结果通常难以获得逼真的效果。为此,本文以空间插值和分形理论为基础,提出由裂缝的几何形态预计参数对地表TIN模型进行重构,以生成裂缝三维模型的方法,并利用ArcEngine平台实现对裂缝的三维可视化。
1 方 法
1.1 地表采动裂缝三维建模总体流程
本文利用裂缝的形态预计参数信息构建裂缝三维模型,该方法以采动前地表TIN模型为基础,根据裂缝分布及形态参数(宽度、深度、倾角、落差等)的预计结果,利用空间插值和分形算法重构TIN模型,实现裂缝的三维可视化。具体方法流程如图1所示。
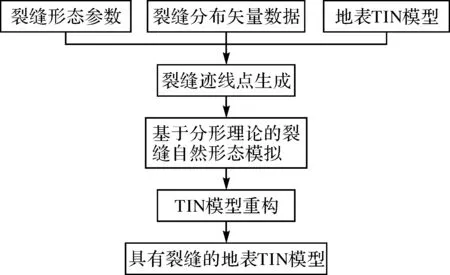
图1 裂缝三维建模流程
1.2 模型输入数据
地表裂缝三维建模涉及两种输入数据:采动前地表的地形数据和裂缝的分布与形态参数。本文采用TIN模型表达采动前地形数据,TIN模型将无重复的散乱数据点集按某种规则(如Delaunay规则)进行三角剖分,使这些散乱点形成连续但不重叠的不规则三角面片网,并以此来描述三维物体的表面[9]。TIN表面模型能以最少的控制点描述地表的空间形态,适当添加控制点可在不同程度上改善细节信息,使其更接近真实的自然状态[10],而减少部分控制点能降低局部工作量而不影响目标的空间形态表达。特别对于含有大量特征(如地性线、断裂线、构造线)的地形,TIN模型能很好地展示这些特征,更精确、高效、合理地表达地表形态[11]。
地表采动裂缝的剖面通常呈“V”字形[12],平面呈带状分布,但由于采动过程差异,地表形成的裂缝会呈现不同的几何形态,常见的裂缝形态包括:直线型裂缝、锯齿型裂缝、复杂曲线裂缝、分叉型裂缝、台阶状裂缝等。对于不同形态的裂缝,其形态参数表达方式也会有所差异,见表1。

表1 裂缝类型及形态参数
建模时,首先导入采动前地表TIN模型和描绘裂缝空间分布的坐标串(以矢量线要素表达),并输入裂缝几何形态参数,具体定义如下:
裂缝宽度:采动裂缝在地表上呈现的宽度,一般在几厘米到几十厘米之间,较宽裂缝可达1 m以上。
裂缝深度:采动裂缝从地表到地下最低点的延伸距离。
裂缝倾角:采动裂缝坡面与水平面的夹角。
1.3 裂缝迹线点生成
本文使用一系列有序离散点描述地表采动裂缝在平面的几何形态,并将这些离散点定义为裂缝的迹线点,包括中线迹线点和边界迹线点。在建模过程中,通过对输入的裂缝矢量线要素的节点进行加密生成中线迹线点,然后以中线迹线点为基础,依据裂缝的几何形态参数推求边界迹线点。由于裂缝是在三维空间中建模,因此需同时计算迹线点的平面坐标与高程,计算方法如下:
1.3.1 迹线点的平面坐标计算
边界迹线点的平面位置按缓冲区生成方法计算,涉及的几何关系如图2所示。

图2 迹线点平面坐标计算

α=arctanxc-xb,yc-yb
(1)
β=arctanxb-xa,yb-ya
(2)
κ=β-α-π/2
(3)
γ=α+κ
(4)
d=t/sinκ
(5)
(6)
式中,t为距离参数,可为正负不同的值。t为正时,b′位于中心折线右侧;t为负时,b′位于中心折线左侧。
1.3.2 迹线点的高程计算
迹线点高程根据地形数据和迹线点的平面位置计算。首先对迹线点进行定位,即确定迹线点位于哪个TIN三角形内(或边线上),然后根据此三角形顶点的高程值利用趋势面分析法计算迹线点高程。
根据三角形顶点坐标和矢量拓扑关系判定迹线点位置的方程为
Li=ai+bix+ciyi=1,2,3
(7)
式中,ai、bi、ci是由三角形顶点pi的坐标xi,yi确定的3个常数,分别可由下面公式求得
(8)
迹线点的定位过程如图3所示。设三角形p1p2p3为搜索的起点,计算点p的面积坐标得L<0,取L1的对应边p2p3的邻接三角形p3p2p4作为下一个判断的三角形。依次进行判断,直至三角形p7p6p8。此时若L1、L2、L3都大于0,则点p在三角形p7p6p8内;若Lii=1,2,3=0,则点p在Li所对应的边上。

图3 迹线点在三角网中的定位过程
若点p位于某三角形内部或其中一条边上,利用趋势面分析法计算迹线点高程值
zx,y=b0+b1x+b2y
(9)
根据式(9)建立法方程
(10)
改写成矩阵形式为
(11)
通过矩阵求逆得
(12)
将b0、b1、b2代入式(7)中,求出迹线点p的高程。若是边界迹线点,则迹线点高程即为求得的高程值;若是中线迹线点,需要在所求高程值基础上减去裂缝深度。
在建模过程中需要注意,过多的迹线点会增加建模的时间成本。因此,建模时应在最大限度地保留裂缝几何形态特征的前提下,尽量减少迹线点的数量,提高建模效率。
1.4 基于分形理论的裂缝自然形态模拟
图4为根据所生成的迹线点呈现出的地表裂缝形态,可以看出这样的几何形态过于规则化,不能逼真反映地表采动裂缝在自然界中的真实形态。

图4 由原始迹线点构成的裂缝几何形态
为模拟地表采动裂缝的真实形态,本文基于分形理论[13-16]使用改进后的中点细分内插方法[17-18],从分数维度视角利用较少的基元和迹线参数推演裂缝边界。内插方法如图5所示。

图5 中点细分内插方法
基元AB为相邻边界迹线点A和迹线点B连接而成的线段,在基元线段AB中点C处沿AB中垂线方向随机地移动一段距离L,得到位移后的新点C1(或C2),将迹线点A、B及新点C1(或C2)顺序相连,得到分形元AC1B。新点的偏移方向由一随机方向参数J迹线。当J>0时,新点在AB右侧生成;当J≤0时,新点在AB左侧生成。将生成的分形元作为新的基元利用相同的方法进行迭代,不断推求出更小的分形元,直到满足给定的迭代次数。新点的坐标方程为
X=XA+XB/2+ΔX
(13)
Y=YA+YB/2+ΔY
(14)
式中,XA、YA分别为迹线点A在X轴和Y轴的坐标分量;XB、YB分别为迹线点B在X轴和Y轴的坐标分量。ΔX、ΔY为与AB长度有关的随机坐标偏移量,可根据迹线点的走向和点C的偏向求算。在保证不会造成地裂缝中断的前提下,X、Y加上随机坐标偏移量后可以使新迹线点C1(或C2)更具不定因素,能模拟裂缝的不规则特征[19-20]。图6展示了加入分形特征后裂缝的自然几何形态。

图6 具有分形特征的裂缝自然几何形态
1.5 TIN模型重构
经过上述步骤生成了具有分形特征的裂缝迹线点,对裂缝进行三维建模,即将这些迹线点融入采动前地表的TIN模型中。为确保在重构后TIN模型中表达出裂缝形态,并避免非裂缝区域发生变形,本研究将裂缝边界设置为隔断线,可以约束TIN的三角网重构仅在非裂缝区域进行,且使裂缝边界上的节点也参与重构。在裂缝区域内,移除TIN模型的原始节点,最终得到可以反映裂缝分布及三维空间形态的TIN模型。
需要注意的是,一旦三角网被修改,必须进行LOP优化。使用Delaunay空外接圆准则检查新生成三角形,如不满足,则调换与相邻三角形所组成的凸四边形的对角线。若对角线发生交换,则继续向相邻三角形扩展此过程,直至满足空外接圆准则或到达三角网边界。
2 原型系统开发与应用实例
2.1 开发环境
基于上述方法,本文以Visual Studio 2010作为开发工具,选择C#为开发语言,利用ArcEngine三维分析类库及相关算法,开发了对多类型复杂地表采动裂缝进行建模与可视化的原型系统。该系统能根据采动前地表TIN模型和裂缝形态参数快速生成三维裂缝模型,还支持从不同角度、方位和距离展示裂缝,并可以通过裂缝所在地质体的任意旋转、移动、漫游、视景变换等操作对地裂缝进行详察。
2.2 应用实例
本文以东峡矿区为试验区,对该区域内因采煤导致的地表裂缝进行建模。东峡煤矿位于中国甘肃省华亭县境内,地理坐标为东经106°40′14″,北纬35°12′04″,西距华亭县城1.8 km。矿区井田内地形复杂,沟壑纵横,冲沟发育,表层几乎全为黄土层所覆盖,主要形成大小不等的梁卯相间的黄土低山丘陵地貌景观。最高海拔为1 701.3 m,最低海拔为1 525.1 m,总体地势东南高,西北低。
近10年来,随着煤炭工业的迅速发展,东峡矿区内先后建设了一批地方煤矿、乡镇煤矿及国有大中型矿井,煤炭工业成为当地的支柱产业之一。但随着开采量的不断增加,采动过程中地表塌陷愈发严重,并出现了各种不同形态的采动裂缝。本文选取了该区域内若干具有典型特点的裂缝,从多个视角展示裂缝三维建模效果。图7展示了裂缝在Google Earth高分辨率影像中的效果和利用本文方法建模的可视化效果。
裂缝群中心位置位于北纬35°12′49.34″、东经106°39′54.00″,裂缝长度从20 m到200 m不等,裂缝类型以曲线型为主。区域1的裂缝为俯视角度,可以看出建模结果准确反映了裂缝的真实位置分布。区域2和区域3为侧视角度,体现出本文方法很好地展示了山体不同高度处的裂缝状态。区域4为裂缝的近距离展示,可以看出带有分形特征的模型逼真地展现了裂缝的不规则自然形态。
为更好地展示生成裂缝后的TIN模型,着重展示研究区中的单条裂缝的效果,如图8所示,左侧为裂缝的渲染图,右侧为对应裂缝的TIN模型,包括节点的分布和连接状态。
2.3 复杂裂缝模拟
为更好地展示本文方法及原型系统在模拟更复杂裂缝形态的效果,通过人工设置裂缝形态参数,模拟出台阶型裂缝、复杂曲线裂缝、弧线型裂缝和交叉型裂缝,分别如图9—图12所示。由图可看出,本文方法能模拟出任意复杂形态的裂缝并能清晰地反映细节信息,无论是对裂缝可视化还是定量空间分析都具有非常好的效果。
3 结 语
地表采动裂缝是伴随着地下煤炭等资源开采的一种表生地质灾害现象,对裂缝的三维建模与可视化研究将促进裂缝的形状、成因研究,并为开采沉陷监测和生态环境恢复提供科学支持,具有重要的实际应用价值。本文结合三维地形建模、分形、空间插值等理论,提出了基于几何形态参数的地表裂缝三维建模方法,并利用ArcEngine平台编程实现了裂缝的三维建模与可视化功能。

图7 东峡矿区地表裂缝建模效果对比

图8 裂缝的TIN模型

图9 台阶型裂缝

图10 复杂曲线裂缝

图11 弧线型裂缝
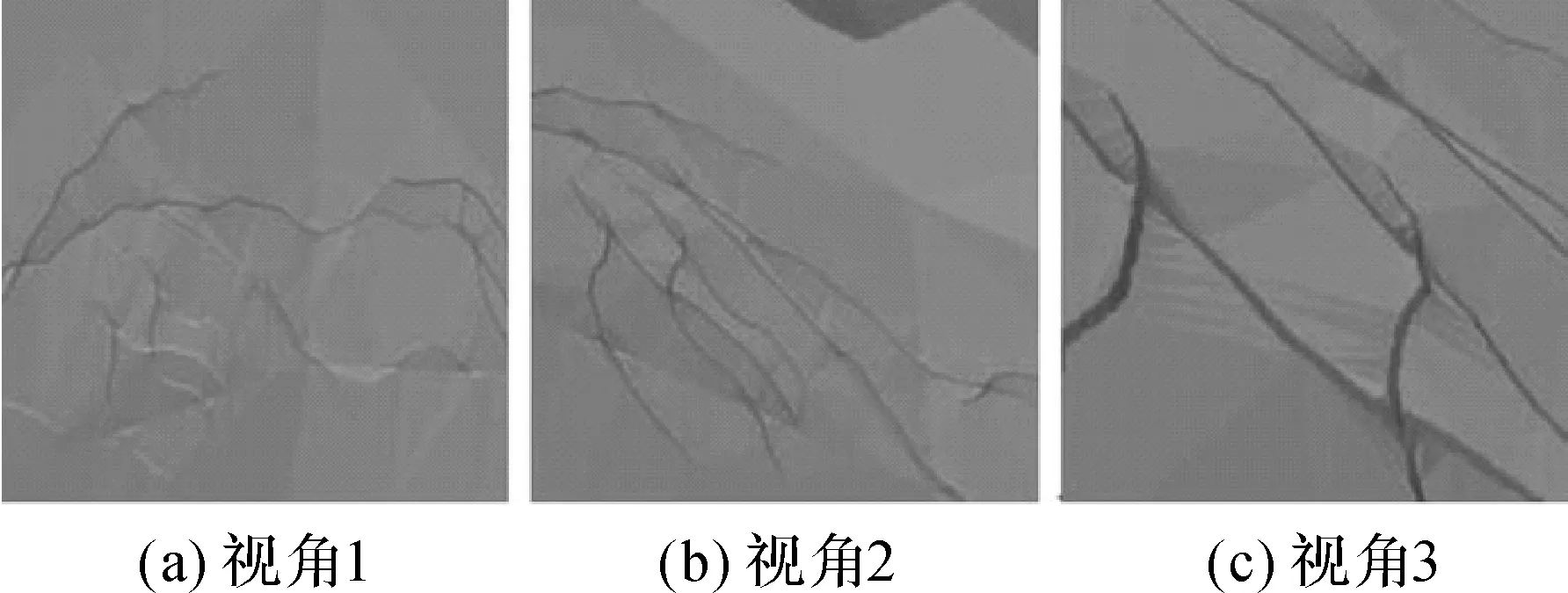
图12 交叉型裂缝
本文选择了东峡矿区为试验区,利用提出的方法对典型区域的地表裂缝进行三维模拟,能真实逼真呈现裂缝的形态、延伸与细节信息。通过与实测数据对比,验证了该方法的有效性和准确性。但本文提出的建模方法、思路,仅仅是对地表采动裂缝在三维环境下分析与模拟的开始,仍然有许多问题需要继续探索,包括数据的多元化、高效存储方式、三维空间分析及应用等方面。
[1] 谢和平,王金华,申宝宏,等.煤炭开采新理念——科学开采与科学产能[J].煤炭学报,2012,37(7):1069-1079.
[2] 胡青峰,崔希民,袁德宝,等.厚煤层开采地表裂缝形成机理与危害性分析[J].采矿与安全工程学报,2012,29(6):864-869.
[3] 张立强,谭玉敏,康志忠,等.一种地质体三维建模与可视化的方法研究[J].中国科学(D辑:地球科学),2009(11):1625-1632.
[4] 张晖,刘超,李妍,等.基于CityEngine的建筑物三维建模技术研究[J].测绘通报,2014(11):108-112.
[5] 张帆,史琼芳,达汉桥.Creator应用于虚拟城市三维建模的关键技术与实践[J].测绘工程,2005,14(4):55-57.
[6] 尹晖,孙梦婷,干喆渊,等.基于SketchUp的输电杆塔三维建模研究[J].测绘通报,2015(4):34-37.
[7] 程朋根,龚健雅,史文中,等.基于似三棱柱体的地质体三维建模与应用研究[J].武汉大学学报(信息科学版),2004,29(7):602-607.
[8] 颜辉武,祝国瑞,徐智勇,等.基于Kriging水文地质层的三维建模与体视化[J].武汉大学学报(信息科学版),2004,29(7):611-614.
[9] 刘永和,张万昌.不规则三角网的几种数据结构及其存储机制研究[J].测绘科学,2010,35(3):115-117,65.
[10] 罗胜,姜挺,江刚武,等.基于原始LiDAR点云TIN模型的建筑物自动提取[J].测绘通报,2012(S1):334-337.
[11] 熊祖强,贺怀建,夏艳华.基于TIN的三维地层建模及可视化技术研究[J].岩土力学,2007,28(9):1954-1958.
[12] 刘一冬,朱琳,于军,等.一种地裂缝地质体三维模型建模方法[J].地理与地理信息科学,2016,32(2):51-54,66.
[13] 李宏艳,王维华,齐庆新,等.基于分形理论的采动裂隙时空演化规律研究[J].煤炭学报,2014,39(6):1023-1030.
[14] 吕秀琴,张毅.分形模拟在DEM内插中的应用[J].测绘科学,2012,37(2):107-109.
[15] ZHU Xiaohua.Fractal Character of China Bedrock Coastline[J].Chinese Journal of Oceanology and Limnology,2004,22(2):130-135.
[16] LIU Chengyu,CHAO Jinlong,GU Wei,et al.On the Surface Roughness Characteristics of the Land Fast Sea-ice in the Bohai Sea[J].Acta Oceanologica Sinica,2014,33(7):97-106.
[17] 梁俊,王琪,刘坤良,等.基于随机中点位移法的三维地形模拟[J].计算机仿真,2005,22(1):213-215.
[18] 梁俊,蒋金龙,赵雪莲,等.随机中点位移法在三维地形插值显示的适用性分析[J].测绘科学,2007,32(3):44-46,193.
[19] 陆娟,王建,朱晓华,等.海岸线分形模拟方法及其应用——以江苏省为例[J].黄渤海海洋,2002,20(2):47-52.
[20] 陆娟,王建,石丽.基于GIS和分形理论的海岸线模拟方法研究[J].中国图象图形学报,2003,8(6):692-696.

