非参数计量经济学中的伪回归诊断

(天津财经大学理工学院,天津300222)

1 引 言

当数据存在趋势时,回归分析可能将无关变量拟合出显著的关联关系.这样的分析会得出错误的结论、做出无效的预测,即发生所谓的虚假回归,给实证研究和预测工作带来风险[1].这就要求学者对模型是否存在伪回归的问题进行诊断,以识别和降低这种风险.在研究当中,参数模型的伪回归诊断已经得到了广泛的重视[2],而非参数模型的伪回归诊断却常常会被人忽视.主要原因在于,非参数模型没有在形式上做主观预设,它们常常被当作最接近真实、决不会犯错的模型.但事实并非如此.在趋势的影响下,参数模型尚且容易错把无关变量拟合出关联关系,作为拟合能力更强的非参数模型,就可能面临更大的伪回归风险.但考虑到非参数模型并没有描述关联关系的表达式,即便模型存在风险,又该诊断什么,如何诊断呢？本文研究了非参数模型的伪回归诊断问题,试图为相关检验方法给出严格的理论论证和较全面的应用参考.

关于伪回归诊断的问题,有些重要的文献做出了有价值的研究.Granger等[3]基于模拟实验,率先研究了单位根过程带给参数模型的伪回归问题,并提出基于DW统计量的回归诊断方法.方法的基本思想是用残差的全局特征来诊断参数模型的表达式是否可靠.在此基础上,Phillips[4,5]研究了单位根过程回归残差的渐进分布特征,推导和完善了方法的理论基础.但该方法并不适合诊断非参数模型.非参数回归是一种关注局部的逐点估计,残差关联机制与参数模型不同,局部之间缺乏相关性.Phillips[6]分析了这个问题,并创造性地提出了局部诊断的思想,研究了数据随机趋势带给局部残差特征的影响.Kasparis等[7]沿用了局部视角的检验设计思想,研究了在多元动态时间序列的分析当中,选错解释变量滞后期时非参数回归的残差异常性质.这些诊断方法的共同思路是,设计统计量考察数据趋势属性带给非参数回归残差的影响,用非参数回归残差的局部特征来诊断原始数据的趋势属性.伪回归诊断的初衷是辨别有风险的回归,但现有的研究并没有把非参数模型中“残差局部特征”和“估计失真风险”的关联关系说清楚,可见局部DW诊断方法的理论基础有待进一步论证.诊断在不同窗宽、不同样本容量的回归当中可能遇到的问题,也有待进一步研究.

本文回顾了随机趋势给非参数模型带来的伪回归风险,并针对现有文献的不足,在Phillips局部诊断思想的基础上,研究了非参数回归中残差局部性质和模型估计风险的关联关系.用数学语言描述回归风险,并通过数学变换,创造性地将回归的诊断问题转化成了级数收敛的检验问题,解释了数据局部特征与局部回归风险之间的联系.还通过模拟实验,考察了不同类型非参估计的伪回归诊断,给出了诊断的一般步骤且验证了诊断的功效.发现,局部残差性质异常是非参数模型估计失真的充分条件,而局部DW检验可以很好地识别这种情况,进而诊断非参数模型的伪回归.文章完善了使用局部特征诊断回归风险的理论基础,具有较强的理论意义；归纳了检验方法在模拟实验中表现出的若干性质,为非参数模型的实际应用提供参考.

2 问题的初探

误设模型的拟合优度通常很低,因此研究常用拟合优度指标来评价模型的可靠性.但当数据存在趋势时,拟合优度指标可能会出现虚高,容易让人把误设的模型当作正确的模型.这就是虚假回归或伪回归.这种“虚假”是由趋势造成的.

在实际经济当中,时间序列的数据生成过程普遍受到多方面因素的影响.其中可能存在一部分影响几乎不随时间推移而有所衰减,这部分影响不断累积,形成了数据的趋势.时间序列的趋势可以分成如下几类,即线性趋势、非线性趋势、变结构现象和随机性趋势[8].趋势有时会给数据分析带来干扰,进而导致模型的误设.

趋势是识别和描述数据生成过程的重要工具.可以运用发现趋势、拟合趋势(通常用虚拟变量、傅立叶展开或非参数形式拟合)和去势等技术,逐步将包含确定性趋势的数据转换成无趋势数据[9].确定性趋势在很大程度上是可预测、可处理的.但如果序列存在随机趋势,情况则变得复杂.随机性趋势表现为数据的长记忆性(常见的有单位根过程和分数单整过程),这种性质打断了时间序列不同位置间数据属性的递推机制,给数据分析工作带来了严重的误导.对于确定存在关联关系的变量,可用误差修正模型建模,探索变量间的影响机制[10].在不确定关联关系时,使用回归方法研究变量关系就可能将无关变量拟合出某种关联关系,研究就是要识别这种回归.

为了直观地展示非参数回归中伪回归的问题,下面用模拟实验举例,使用非参数模型对单位根过程做回归分析.设三个随机序列ut,vt,ξt服从标准正态分布,用它们定义三个非平稳过程xt,yt,zt.首先生成单位根过程x序列；然后借助x序列生成y序列,此处不失一般性地设定二者存在正相关的线性函数关系；最后生成了一个与前两个序列无关的单位根过程z序列.

数据生成过程的数学表达式如下

其中k取正整数,用来控制y序列的波动幅度,令k=1,序列设为100期.

对生成的数据多次重复下面的回归,即式(4)～式(6).

当变量间相关系数较高时,回归容易产生较高的拟合优度.在考察回归拟合优度之前,不妨先查看自变量和因变量间的皮尔逊相关系数,实验重复1 000次,结果见图1.

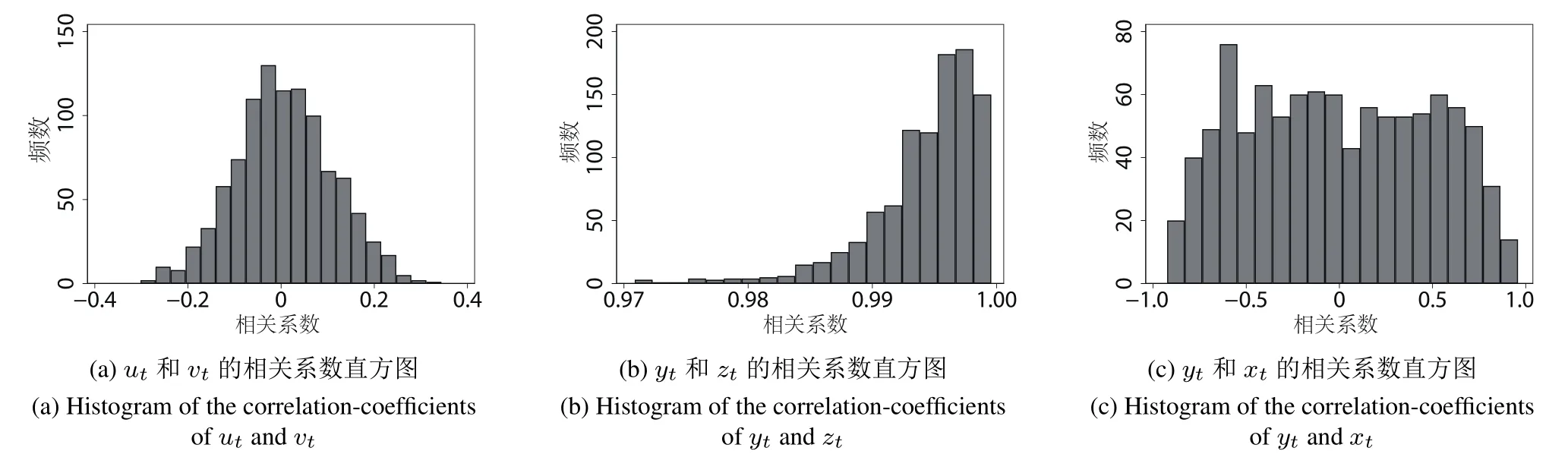
图1 相关系数直方图Fig.1 Histogram of the correlation-coefficients

根据式(1)～式(3)可以看出,y序列与x序列存在函数关系,而y与z和v与u均不存在关联关系.由图1可以看出,当数据不存在随机趋势,无关序列不会呈现出显著的相关特征,v与u的相关系数集中在(-0.2,0.2)；当数据存在随机趋势时,无关序列相关系数尽管期望为0,但有时表现出显著的正相关,有时表现出显著的负相关,实验产生的相关系数几乎是均匀分布在(-1,1)的区间里；如果数据本身存在关联关系,y与x表现出显著的相关关系,与实验的设定相符,相关系数集中在(0.97,1.00)的区间里.

比较三个回归的拟合优度.回归1中的变量不存在趋势,拟合优度集中在0附近.用非参数回归分析非平稳数据(即回归2和回归3)是下面研究的重点.采用不同窗宽实施模拟实验研究这两组回归的拟合优度,研究结果见图2,图(a),图(b)和图(c)采用的窗宽依次为h=n-1/2.5,h=n-1/3和h=n-1/4.

不妨将回归2称为虚假回归,回归3称为真实回归.图2显示,虚假回归的拟合优度几乎均匀分布在(0,1)的区间里,而真实回归的拟合优度集中在1附近.在随机趋势的影响下,虽然z与y之间不存在关联关系,但有时会得到不错的拟合优度.拟合优度指标是失效的.窗宽的不同没有造成显著的差异.

研究还做了另一组实验.令k=10,即放大被解释变量的波动幅度,比较真实回归与虚假回归的拟合优度,结果见表1.

根据实验设定可知,用z来预测y既没有经济意义,又没有实用价值.但当因变量有较大波动幅度时,有超过5%的概率,伪回归的模型看上去更有效.如果单纯依据拟合优度选择模型,有5%以上的概率误选伪回归的模型做分析和预测.

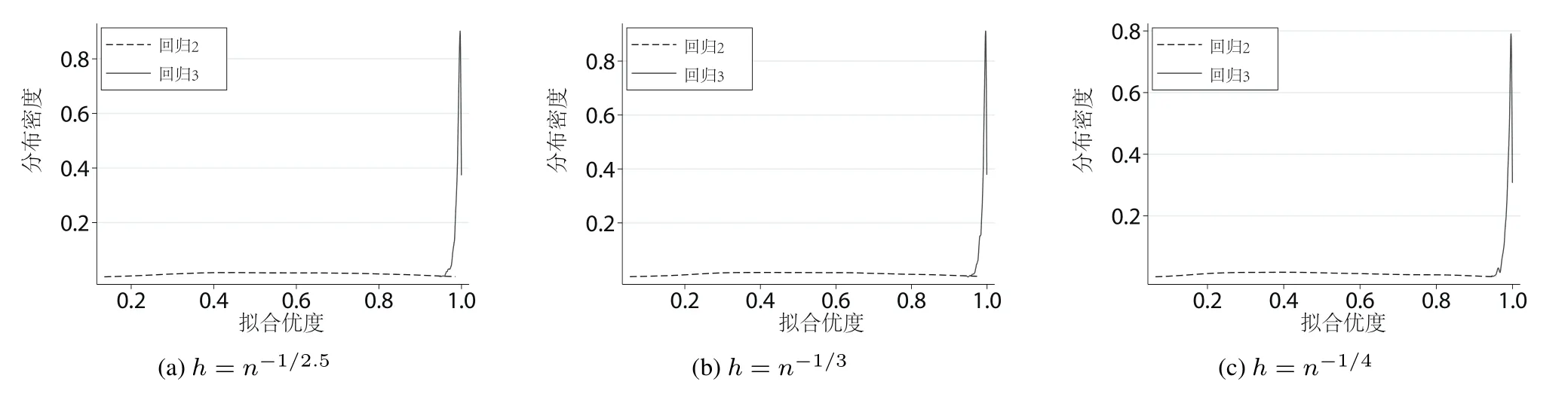
图2 回归2和回归3的拟合优度经验分布图Fig.2 Empirical distribution of goodness of fit for regression 2 and regression 3

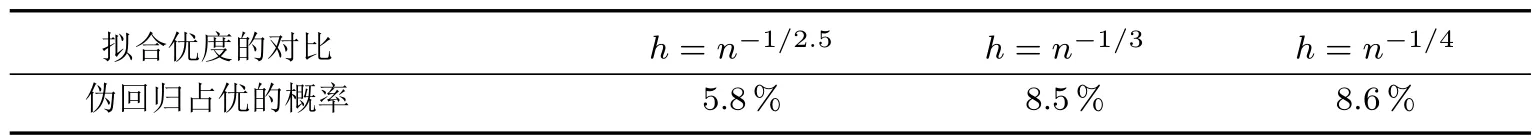
表1 凭拟合优度选解释变量时犯错的概率(k=10)Table 1 The probability of choosing wrong when explanatory variables are selected by goodness of fit(k=10)

可以得到一个初步的结论,对非平稳数据做非参数回归时,拟合优度指标无效.模型需要新的诊断工具来识别虚假的回归.

3 基于残差特征的模型诊断方法

当数据生成过程存在随机趋势时,拟合优度指标不再可靠,DW统计量变得重要.无论是参数模型还是非参数模型,都对残差序列做了“相互独立”的假设.如果估计出的残差违背了独立性的假设,对模型的估计可能存在失真.反过来看,若模型设定有误,所估计出的残差通常存在序列相关.利用DW指标对残差做检验,可以帮助识别这类模型.

存在伪回归问题的参数模型,具有三个特征,分别是异常的关联关系、较高的拟合优度和极低的DW统计量.对参数模型的伪回归诊断,主要是借助DW统计量对残差做序列相关检验.若DW统计量存在异常,可以推断模型存在虚假回归.

非参数残差的形成机制有所不同.非参数回归是一种逐点估计,局部与局部之间缺乏关联.但对点估计和局部估计而言,仍可以用残差的函数来描述估计面临的风险.不同位置的残差应当具有不同的影响权重.为了评价估计所面临的风险以实现对非参数模型的诊断,需要基于DW统计量的思想,设计新的统计量.下面基于非参数核回归模型,研究残差特征与估计风险的关系,给出伪回归检验的设计思路和理论依据.

3.1 非参数核回归的模型设定

非参数回归的一般形式为[11]

其中x为解释变量,y为被解释变量,t为误差项的估计值,是对被解释变量的核回归估计,其形式为

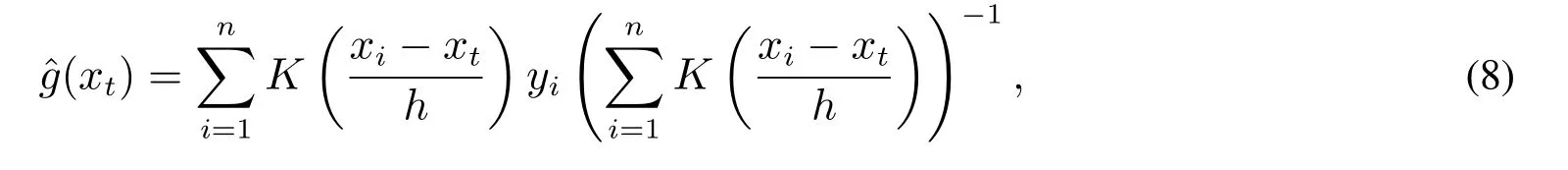
其中K(·)是核函数,h为窗宽.

在非参数模型当中,窗宽的选择对模型的估计有显著的影响.当窗宽取无穷大时,非参数模型退化成线性参数模型；当窗宽无穷小时,非参数模型研究的是极小区间内的关系,甚至可能会浓缩到一个点.对伪回归的诊断,就有逐点视角、局部视角和全局视角等三个角度.全局视角的分析与参数模型一致,下面主要讨论“逐点视角”和“局部视角”.

3.2 非参数点估计的风险及伪回归残差特征

非参核回归所做的点估计,本质上是用多个观测值的加权平均来估计被解释变量,可将该估算方法的表达式改写成

其中wt,i表示估计yi时yt所占的权重,其表达式为

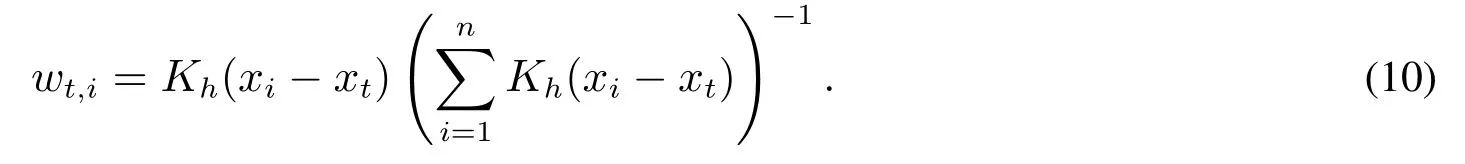
在x与y间函数关系连续的假设下,如果观测点的x取值相邻,其y的取值也应该相邻；若xi与xj的差在约定的范围内,对任何i̸j,都可以用yj作为估计yi的参考；若xi与xj的观测值足够临近,yj与yi也该接近,所以yj将被赋予较高的权重.当数据存在异常值时,加权平均的方法不再适用.举一个极端的例子,设yi是一个显著的离群值,以至于它与其它y观测值的差别很大,而其它y观测值之间的差别小到可以忽略,就不应该用y的加权平均值当作yi的估计值.以yj来估计yi是存在风险的,不同位置带给估计的风险具有不同的权重.

非参数模型的点估计风险可以用级数来描述,其表达形式为

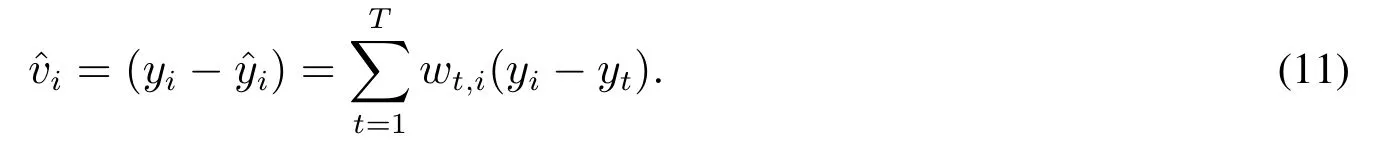
在这个级数中,如果相邻数项相关系数为1,点估计值不会随着样本容量的增加而收敛,估计风险将失控.在wt,i(yi-yt)序列存在高度关联的特征时,模型的估计是不可靠的.前人的研究主要关注随机趋势给残差特征带来的影响.本文特别关注残差数据特征和回归可靠性之间的关系,并将回归风险的诊断问题转化成级数收敛的检验问题.

3.3 局部的非参估计风险及对应的残差特征

对点估计风险的检验,需要检验wt,i(yi-yt)序列的相关特征,这要求yi为已知量.然而在实际预测工作中,待预测的观测值通常是未知量.诊断对某个待预测点的非参估计,需要引入“局部视角”,也就是以该点为观察点,考察对估计该点产生影响的整个局部,诊断非参数回归在这个局部的表现.在这个局部里,各位置的i都需要考虑进来.

定义一个待预测点(xobs,E[y|xobs]),因变量的非参估计值为

根据定义,待预测点的y为E[y|xobs],可以将估计风险定义成估计值的偏差,并可表达为

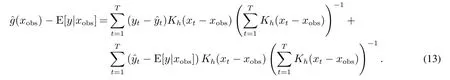
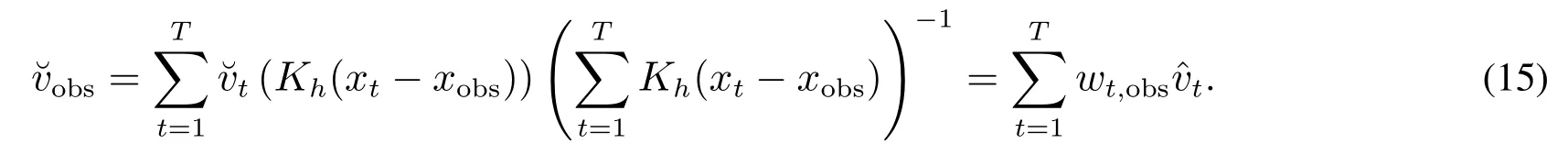
判断一个局部的回归质量,要考察回归在局部范围内每一处的估计风险.从观测点的角度出发,不同位置的风险应该被赋予不同的权重.用加权的思想设计局部DW检验,可以识别这种风险.从另一个角度来看,检验wt,obst的序列相关特征,可以看成检验t序列是否满足独立性假设的一种非线性方法.

3.4 残差序列相关特征的识别

经过上面的研究,已经把回归风险的诊断问题转化成了残差性质的诊断问题.在研究非参数回归残差诊断之前,首先回顾参数模型的情况.

DW统计量是检验参数模型残差性质的重要工具,其表达式为

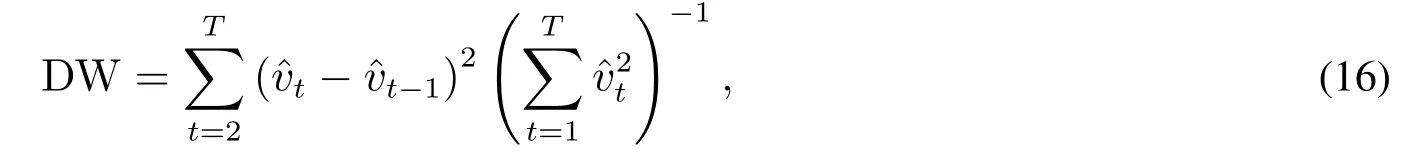
其中T为样本容量.

使用参数模型研究问题,最终会给出确定的模型形式及内部参数的估计值,以表述在全部定义域内解释变量如何影响被解释变量.模型每一处的残差都有平等的地位,在构造统计量时拥有相同的权重.对非参数回归模型的诊断,则有所不同.非参数模型中没有一个代表全局的表达式可供诊断,不同局部间的关联性随间隔变大而变弱.诊断特定局部的回归时,其它位置的残差不再具有平等的地位.Phillips[6]基于相似的思想,率先定义了局部拟合优度和局部DW,其表达式分别为

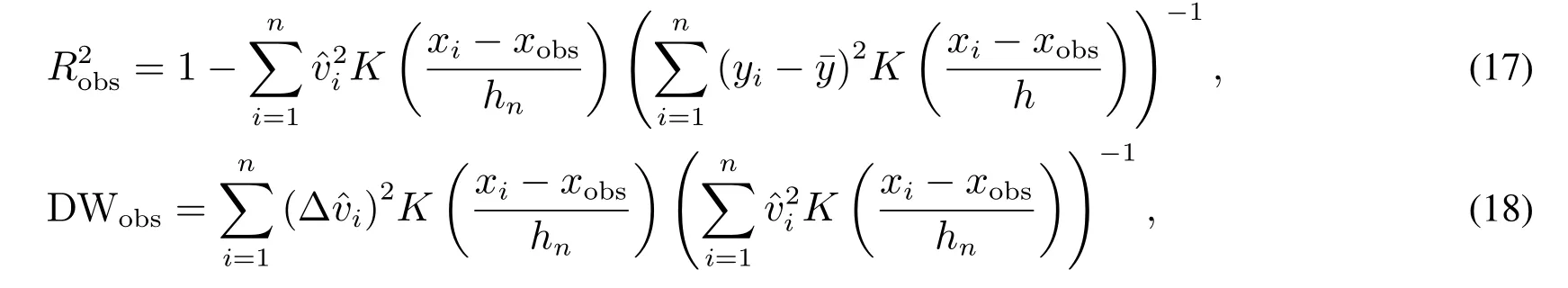
对一组无关非平稳序列做非参数回归时,局部DW统计量在h→0且Th→∞的假设下有稳定的渐进分布(参见文献[6]中的定理3),可以很好地描述变量趋势带给模型的残差特征.模型如果具有这种残差特征,其估计的过程就会存在风险,因此局部DW检验可以用来诊断模型的虚假回归.

当数据存在随机趋势,拟合优度指标不再可靠时,局部DW统计量直接用残差拟合值构造函数,相当程度上减弱了观测值非平稳带给检验统计量的干扰.其背后的原理在于,加权后的残差可以更恰当地描述非参数模型所面临的回归风险.局部DW统计量所发现的残差相关性,已经不再是简单线性相关关系,而是非参数意义上的相关关系.

综上所述,可以依据残差存在的这种非线性序列相关性来推断非参数模型估计存在的风险；局部DW统计量可以识别这种序列相关,进而帮助识别模型的误设；统计量在渐进意义上是可靠的.实际的数据分析工作中,讨论统计量在渐进意义上是否有效固然重要,其渐进速度同样对检验的实际应用产生重大影响.下面通过模拟实验,研究实际应用当中,局部DW统计量能否有效地诊断出非参数模型中的伪回归问题.

4 模拟实验

通过模拟实验评估局部DW检验在非参数模型中的表现.实验的目的在于,一方面评估局部DW检验在非平稳数据非参数回归中识别伪回归的功效,为理论提供支持；另一方面估算恰当的统计量拒绝域,为实际研究提供参考.考虑到非参数回归有样本容量T和窗宽h两个重要的参数,实验对不同样本容量和不同窗宽分别做了考察,试图发现局部DW统计量如何随模型参数变化而变化.

生成随机序列xt、yt和zt,序列生成方式与前文中的x、y和z相对应.yt与xt存在稳定的关联关系,而与zt无关.序列均存在随机趋势,波动幅度参数k=1.用前文中的回归2和回归3对yt做回归分析,用局部DW检验对回归做诊断,在实验中观察检验的表现.在实验之前,需要对核函数的形式做预设.在非参数回归当中,通常要根据数据关联关系来选择核函数,实验选用了常见的正态核函数.在检验当中,需要借助核函数来排除局部间的干扰,因此在计算局部DW统计量时,原则上不可以使用正态核,实验选择了较简单的均匀核.如何更恰当地选择核函数,有待进一步的研究.

原假设为H0:模型的解释变量与被解释变量存在关联关系.备择假设为H1:模型错误地选择了无关的解释变量.

回归3使用x做自变量,原假设H0成立.对这类回归做检验,应该以极小的概率拒绝H0(犯弃真错误的概率较小),同时以较大的概率拒绝H1(犯取伪错误的概率也较小).回归2使用z做自变量时,备择假设H1成立.对这类回归做检验,应该以较大的概率拒绝H0,以较小的概率拒绝H1.运用模拟数据,分别计算两组回归中的局部DW指标,结果见图3,

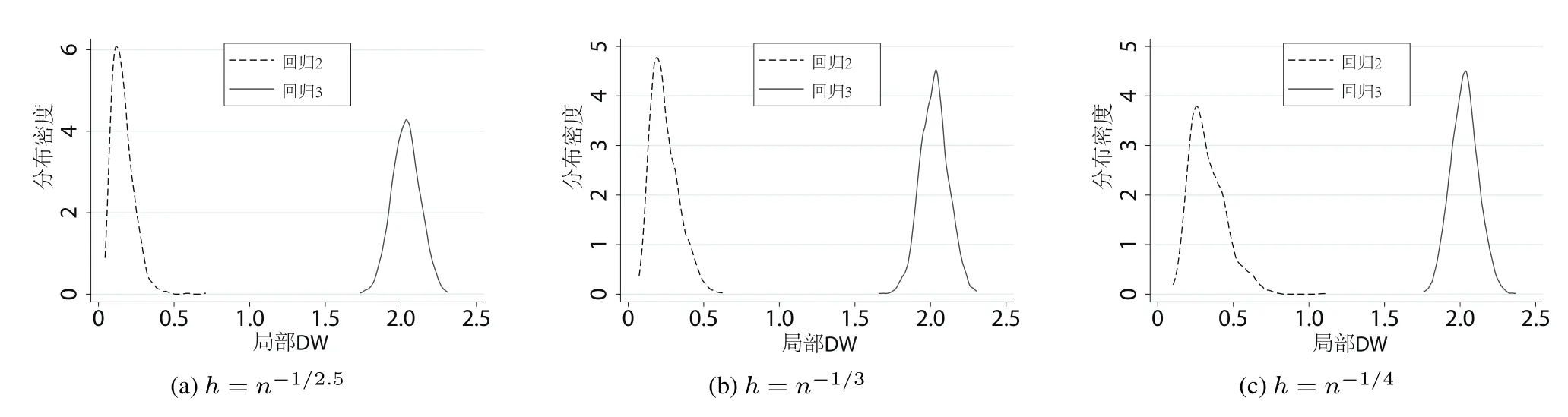
图3 回归2和回归3在中位点附近的局部DW统计量经验分布图Fig.3 Empirical distribution of local-DW-statistics near the median site of regression 2 and regression 3

图3中从左到右的三条曲线分别对应三组不同的实验,图(a),图(b)和图(c)采用的窗宽依次为h=n-1/2.5,h=n-1/3和h=n-1/4,每组实验重复1 000次.观察图3可知,回归2的局部DW统计量取值集中在0附近,而回归3的局部DW统计量取值集中在2附近.数据的随机趋势并没有给局部DW统计量的表现带来干扰.

继续借助实验研究局部DW统计量的检验临界值.采用n-1/2.5、n-1/3和n-1/4三个窗宽,选择1/4分位点、中位点和3/4分位点为回归检验的观测点,划定三个“待观测局部”,选择T=100,500,1 000,三个样本容量.首先考察中位点附近,局部DW检验的表现,实验结果见表2.

表2 中位点附近做局部DW检验时回归落入拒绝域的概率表Table 2 Probability table of falling into the rejection domain when local DW test is performed near the midpoint

在中位点诊断非参数模型,局部DW检验的功效较好.尤其是在局部数据足够多时(即窗宽大、样本多时),局部DW统计量可以显著地区分真实回归和虚假回归.下面观察1/4分位点和3/4分位点的情况,实验结果见表3.

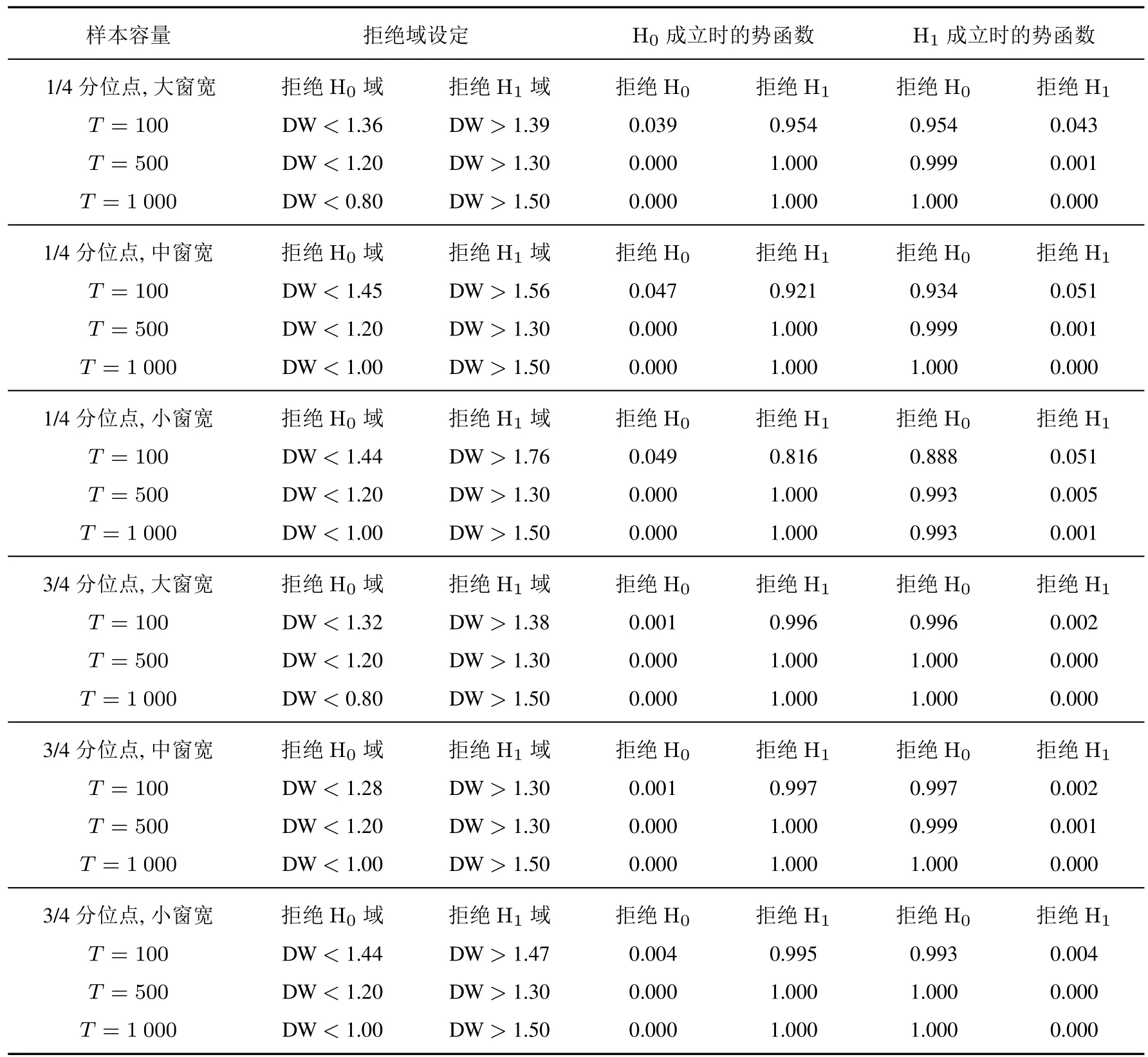
表3 分位点附近做局部DW检验时回归落入拒绝域的概率表Table 3 Probability table of falling into the rejection domain when local DW test is performed near the locus

诊断1/4和3/4分位点的非参数估计,局部DW检验的功效有所下降.尤其是在小样本、小窗宽的情况下,统计量分布不稳定.将弃真概率设置到0.01附近时,取伪概率普遍接近或超过0.1；当弃真概率设置到0.05附近,取伪概率的表现才有所改观.当样本容量超过500后,局部DW统计量分布趋于稳定,检验功效有所提高.

以上研究表明,局部DW检验可以较好地识别非平稳数据非参数回归中的伪回归.实验发现,局部DW检验的功效呈现出一条基本规律,即有效样本越多,检验功效越好.当样本容量较小时(如T＜100),统计量波动尺度较大,检验的功效也较差；在大样本下,检验功效普遍较好.窗宽越小(所容纳的观测值也就越少),检验的功效越差；当窗宽变大,检验功效将得到显著提升.当样本数据来自总体的边缘,检验功效较差；而对中位点附近的非参估计做诊断,检验功效较好

5 结束语

本文对非参数模型中的伪回归诊断问题进行了研究.与参数模型相似,非参数模型同样可能发生伪回归.通过研究非参数核回归的估计风险与残差特征发现,模型的估计风险可以表述成级数部分和的形式,而残差序列中特定的相关特征会造成级数的发散即模型估计风险的失控；用加权后残差构造的局部DW统计量,可以检验这种序列相关.这些论证为使用局部DW检验方法来预警回归风险和诊断虚假回归提供了坚实的理论依据.模拟实验发现,局部DW检验具有良好的功效.在原假设成立和备择假设成立两种情况下,局部DW统计量都可以较快地趋近于对应的稳定分布.应用局部DW检验时,可根据实际的样本容量和窗宽设定来参考本文中相应的统计量临界值.