正负反馈交替论模型及应用

林 屹严洪森

(1.东南大学自动化学院,江苏南京210096；2.东南大学复杂工程系统测量与控制教育部重点实验室,江苏南京210096；3.南京信息工程大学信息与控制学院,江苏南京210044)

1 引 言

对于系统状态变化规律的研究是非线性系统理论的一个重要组成部分.实际物质系统中,一些系统的状态变化往往存在由量变到质变,从一个稳定阶段过渡到另一个稳定阶段的现象,从而不断呈现出“平稳→剧变→再平稳→再剧变”的过程.1972年Thom提出突变理论,从分叉理论和奇异性理论出发,研究了非线性系统从一个稳定状态向另一个稳定状态的跃迁,归纳出折迭、尖点等七类突变类型的几何模型[1].目前,基于突变理论的应用研究也已经在很多学科领域取得了广泛成果[2-8].此外,虽然可查文献较少,但仍有一些文献从量变到质变的角度讨论了系统状态的这一变化规律.文献[9]从复杂系统的观点对其进行了定性讨论及阐述.文献[10]则结合系统状态的这一变化规律,根据对立模糊集和相对差异函数定义,提出了基于模糊理论的系统量变与质变判据.上述这些研究,从不同角度探讨了系统状态由量变到质变而呈现出的“平稳→剧变→再平稳→再剧变”这一变化规律.然而,在对于系统状态变化规律的研究[9-12]中,尚未从动态数学模型的角度展开研究.此外,在现有的基于数据的建模及预测方法[13-18]中,也未曾从稳定性分离的角度考虑建模问题.

鉴于此,严洪森[19]提出了正负反馈交替论的思想,即事物的变化往往具有从基于负反馈的量变到基于正反馈的质变的过程,量变到一定程度引起质变,产生新质,然后,在新质的基础上又开始新的量变,于是,质变量变交替出现,与此相应,正负反馈也交替出现.

本文在正负反馈交替论思想的基础上,提出了正负反馈交替论的动态数学模型.用叠加多个死区函数反映系统状态不同剧变期由于能量爆发造成的正反馈作用,将系统状态稳定性分离,不从系统的内在机理出发,而是通过系统内在机理的外部表征数据,建立系统的动力学模型,从动态数学模型的角度探讨系统状态由量变到质变所呈现出“平稳→剧变→再平稳→再剧变”的这一变化规律.本文以状态变化具有典型上述演变规律的非线性时间序列为例,进行建模仿真及预测研究,结果表明了该正负反馈交替论模型在非线性时间序列建模中的有效性.以一个新的角度对物质系统中一些存在状态由量变到质变所呈现出的“平稳→剧变→再平稳→再剧变”这一变化规律进行了探讨.

2 正负反馈交替论模型

正负反馈交替论是将正、负反馈思想与系统的一般变化规律相结合,其具体思想表述如下:

物质系统的某一状态往往可以由某一个(或一些)参数加以表征.当该参数变化在小范围内波动时,处于能量的积累过程,系统状态表现出平稳变化；当能量积累到一定程度而爆发,此时状态参数变化量急剧增大,系统状态产生剧变；随着剧变的发生,系统状态表现出具有明显差异的动态特性,同时由于剧变后能量的消散,状态参数的变化量减小,再次呈现小范围的波动,进入新的平稳期,能量重新积累等待下一次的爆发.系统状态变化量在小范围内波动时,可等效为负反馈的作用结果,系统稳定；剧变发生时,状态变化量不断增大,此时可等效为正反馈的作用结果,系统表现为不稳定状态.随着这种能量的不断积累、爆发与消散,等效正负反馈的交替出现,系统不断呈现出“平稳→剧变→再平稳→再剧变”的一般变化规律.

能量爆发会造成状态的变化量急剧增加,这种不断增加的变化量就像是系统增加了一个阶跃信号后的正反馈,而这种正反馈造成系统不稳定,从而导致剧变的发生,这种等效正反馈作用可以用死区函数及其叠加来反映.

定义1死区函数定义为dez(Δx,αBP,αBN),

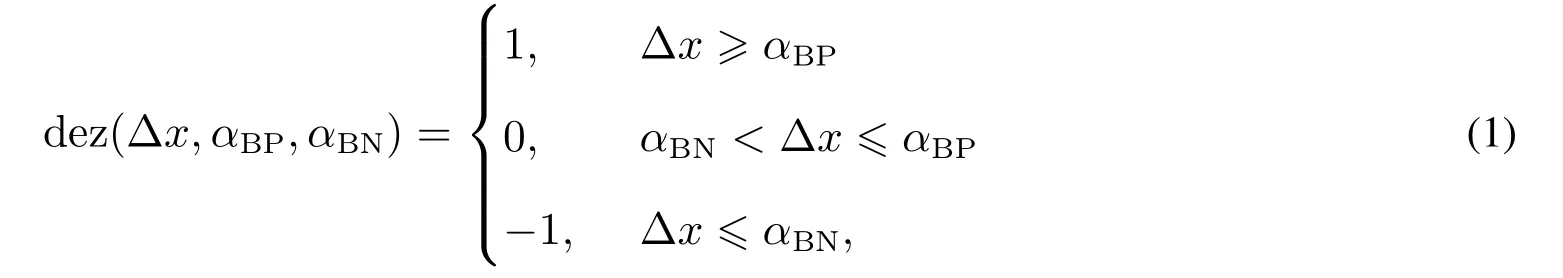
其中Δx为状态变量的变化量,αBP为能量爆发时的增量的正向初值,即正反馈的状态变化量正向起点,αBN为能量爆发时的增量的负向初值,即正反馈的状态变化量负向起点.

当系统状态变化量达到正向阈值αBP(或负向阈值αBN)时,正反馈起作用,图1为该死区函数示意图.

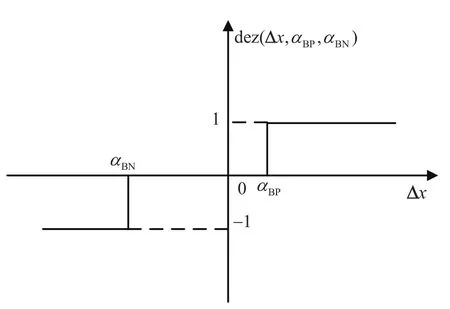
图1 死区函数dez(Δx,αBP,αBN)Fig.1 Dead-zone function dez(Δx,αBP,αBN)

能量的爆发只能持续一段时间,当系统能量爆发后系统状态的变化量的增量达到更高的正向数值αEP(或负向阈值αEN)后,系统能量释放结束,正反馈随之消失,此时αEP称为增量的正向终值,αEN称为增量的负向终值.

系统能量爆发过程中施加于系统上的等效正反馈作用可以通过上述两个死区函数的相减来获得.令该相减后获得的死区函数为死区叠加函数sdez(Δx,αBP,αEP,αBN,αEN),具体定义如式(2),图2为死区叠加函数示意图.

定义2死区叠加函数定义为sdez(Δx,αBP,αEP,αBN,αEN),

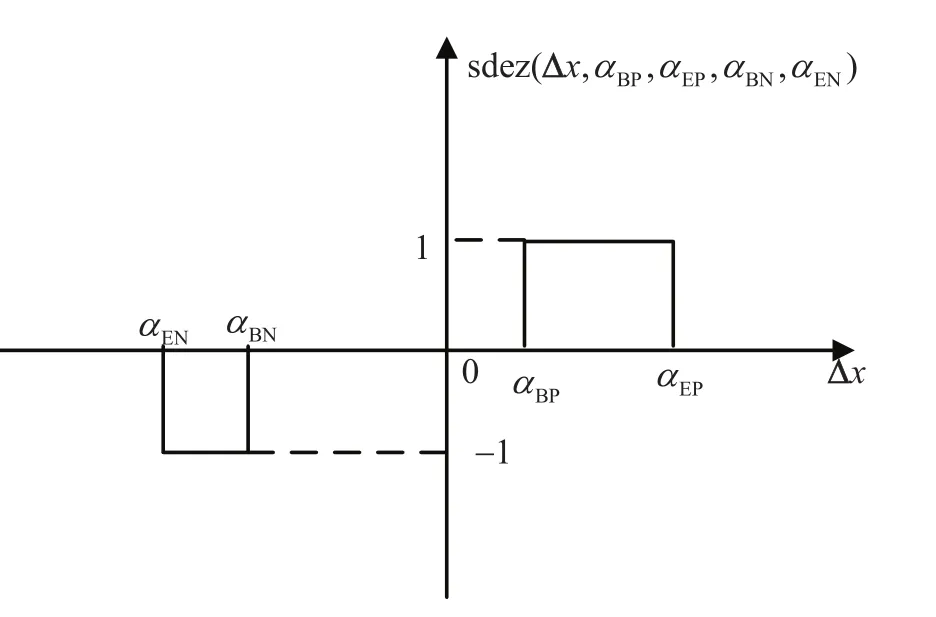
图 2 死区叠加函数 sdez(Δx,αBP,αEP,αBN,αEN)Fig.2 Dead-zone superimposed function sdez(Δx,αBP,αEP,αBN,αEN)

关于变量及死区叠加函数有如下结论.

定理1对于x1,x2,...,xn,zl1,zl2,...,zlµ,l=1,2,...,n的可展成泰勒级数的任意非线性函数h,有

其中zlj=sdez(Δxl,αlBPj,αlEPj,αlBNj,αlENj),l=1,2,...,n;j=1,2,...,µ.

定理1的具体证明过程见本文附录.

定理 2对于自变量为x,sdez(Δx,αBP1,αEP1,αBN1,αEN1),sdez(Δx,αBP2,αEP2,αBN2,αEN2),...,sdez(Δx,αBPµ,αEPµ,αBNµ,αENµ)的可展成泰勒级数的任意非线性函数向量h,有

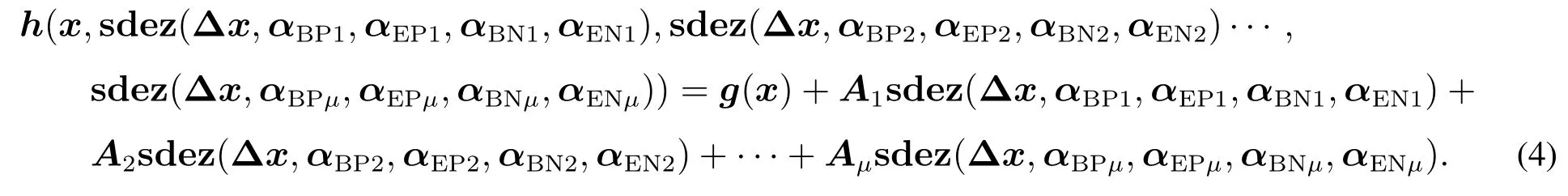
证明根据定理1,将式(4)展开成标量形式,如方程(5)所示.

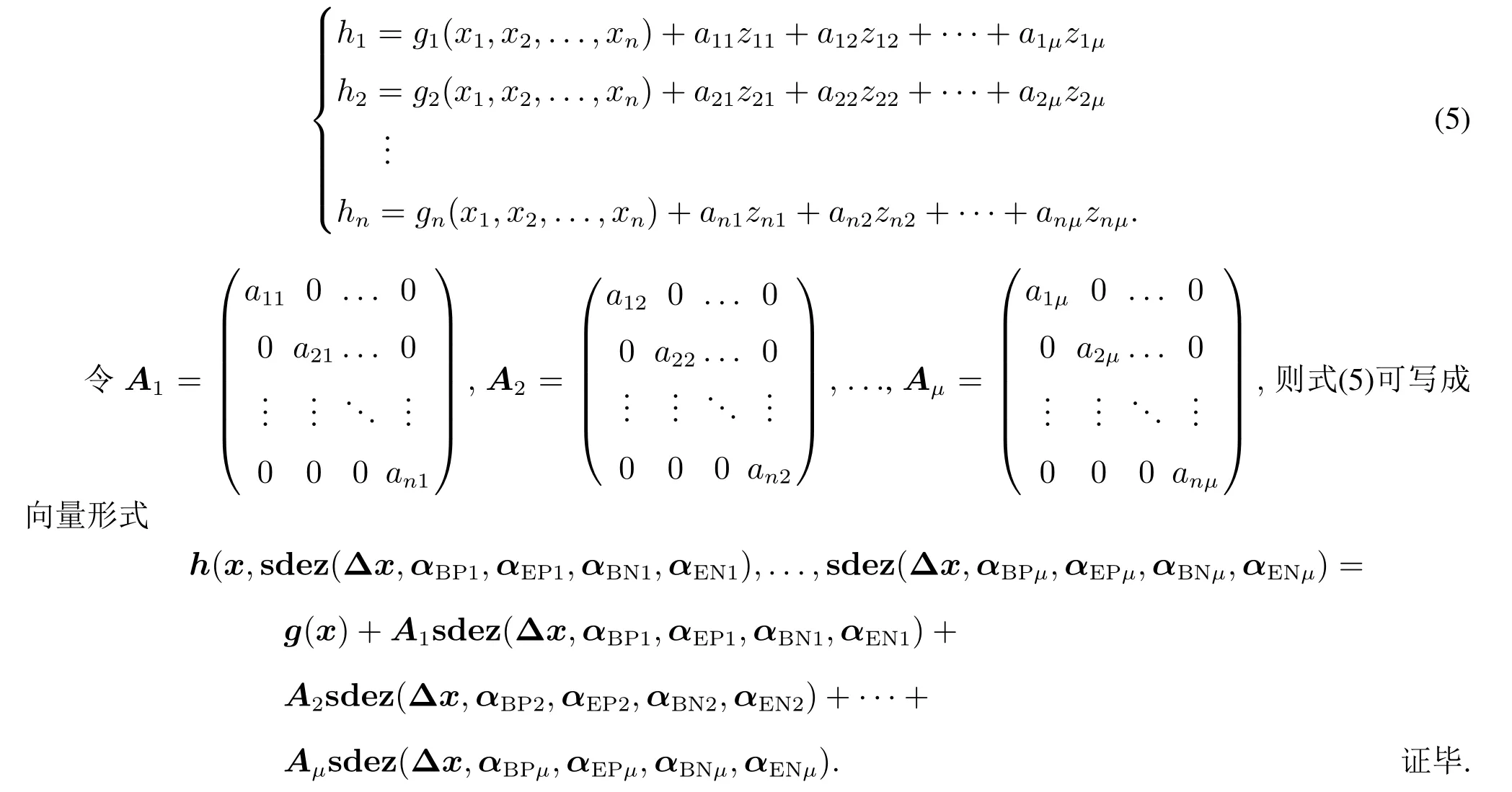
系统动力学方程的一般形式为

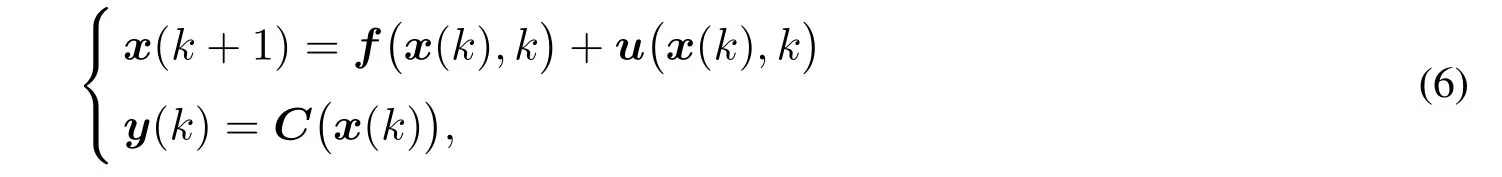
其中x(k)为系统的状态向量,y(k)为系统的输出向量,C为输出矩阵,f(x(k),k)为反映系统自身属性函数,u(x(k),k)为反映状态控制属性函数.

由定理2可知,结合正负反馈交替论思想,式(6)中状态控制属性函数u(x(k),k)可等效为两个部分,一个部分为平稳区系统状态呈现变化量小范围波动时的等效负反馈g(x(k),k),另一个部分为变化量不断增加的导致特性发生改变的等效正反馈,在“平稳→剧变→再平稳→再剧变”的过程中,不同的剧变分别具有各自的等效正反馈函数

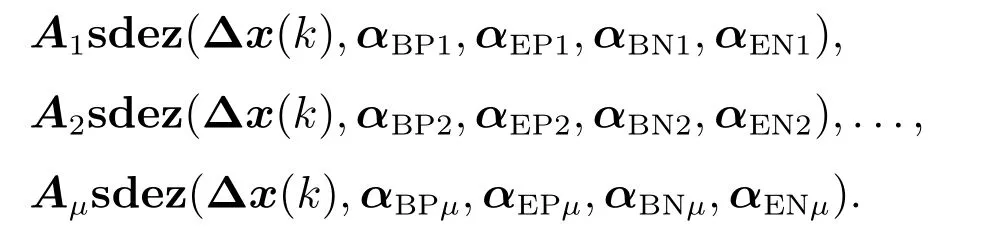
因此,根据定理2可将反映状态控制属性的函数向量u(x(k),k)表示为

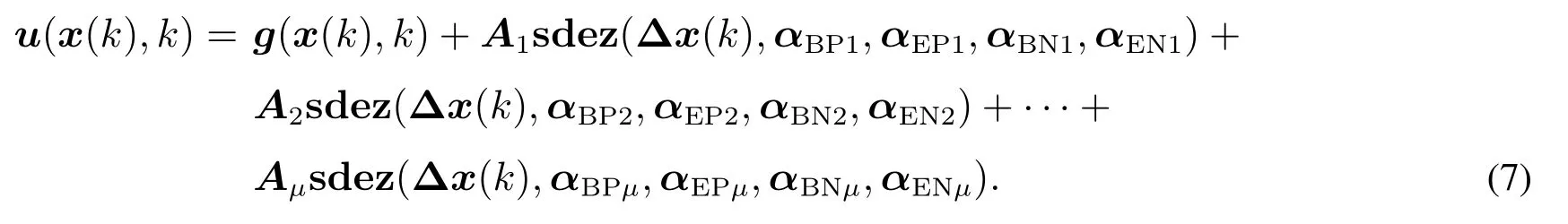
将式(7)代入式(6),便可得到系统闭环动态模型的一般形式.其系统状态的标量形式为

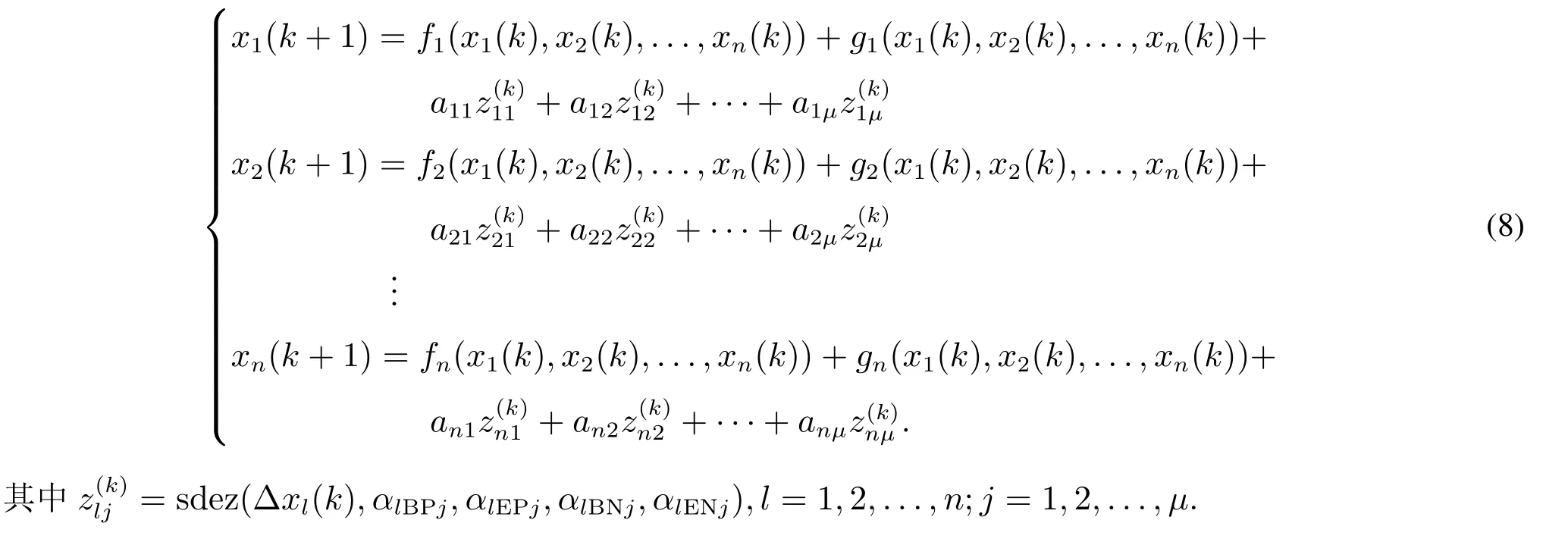
3 正负反馈交替论模型的建立

由于式(8)中fl(x1(k),x2(k),...,xn(k)),以及gl(x1(k),x2(k),...,xn(k)),l=1,2,...,n可以用多维泰勒网展开式逼近[20],均为xi(k),i=1,2,...,n的非线性函数,可将两者合并,至此便得到了正负反馈交替论的动态数学模型,如式(9)所示.

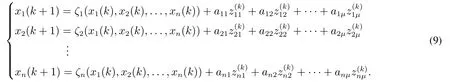
该模型针对系统状态由量变到质变而呈现出的“平稳→剧变→再平稳→再剧变”这一变化规律,从等效正负反馈的角度,将稳定性分离,其平稳区函数ζl(x1(k),x2(k),...,xn(k)),l=1,2,...,n可以通过多维泰勒网方法获得.而数据剧烈变化段的各剧变区正反馈参数,包括死区函数系数alσ、各死区叠加函数的正反馈的状态变化量正向起点αlBPσ(或负向起点αlBNσ),以及正反馈的状态变化量正向终点αlEPσ(或负向终点αlENσ),l=1,2,...,n;σ=1,2,...,µ需要根据对剧变区的数据剧烈变化的分析获取.

3.1 平稳区模型参数求解

多维泰勒网结构如图3[20].模型式(10)中各平稳区函数ζl(x1(k),x2(k),...,xn(k)),l=1,2,...,n的参数可以通过多维泰勒网的参数求解获得.网络输入为xM(k)=(xM1(k),xM2(k),...,xMn(k))T；中间层为各幂次乘积项单元和相应连接权值,λl={λl,1,λl,2,...,λl,w},l=1,2,...,n为连接线上的权值集合；网络输出为xM(k+1)=(xM1(k+1),xM2(k+1),...,xMn(k+1))T.

多维泰勒网络模型可用数学表达式表示为[20]

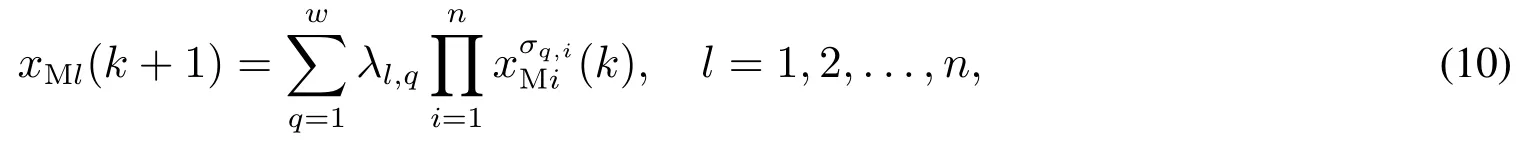
其中n为输入层和输出层节点数,w为隐层节点总数,λl=(λl,1,λl,2,...,λl,w)T,l=1,2,...,n为连接中间层节点与网络输出层第l个节点的输出权值向量,σq,i为各输出节点的第q个乘积项中变量xMi(k)的幂次.

由多维泰勒网的结构和式(10)可知,对于xM1(k),xM2(k),...,xMn(k)的可展成泰勒级数的任意非线性函数多元函数ζl(xM1(k),xM2(k),...,xMn(k)),l=1,2,...,n,即xMl(k+1),可用多维泰勒网方法描述为

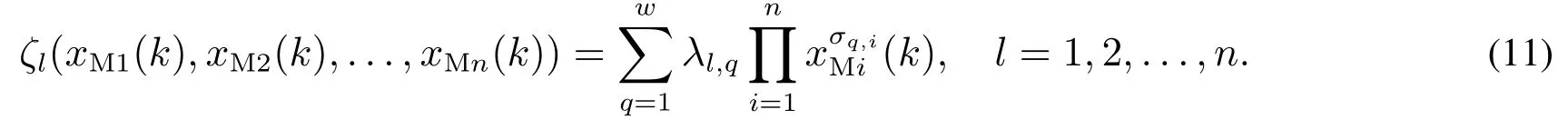
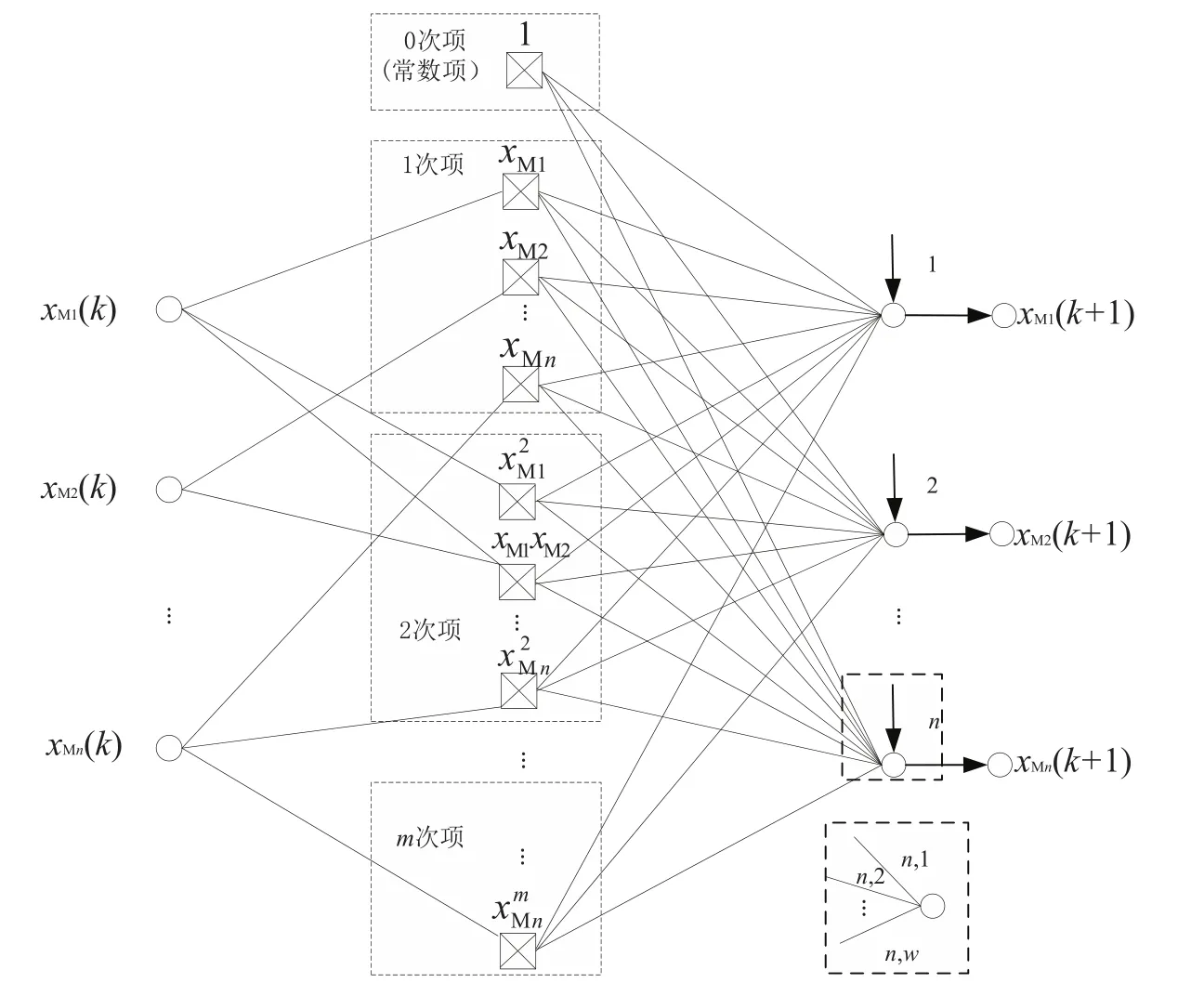
图3 多维泰勒网模型Fig.3 The model of multi-dimensional Taylor network

求解正负反馈交替论模型的平稳区参数就是通过网络学习获得平稳区多维泰勒网表达式中各个乘积项的权值.由于多维泰勒网的输入量就是正负反馈交替论模型的输入量,即

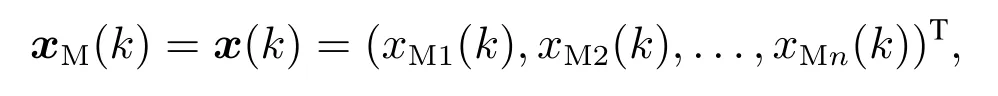
故如式(11)所示的多维泰勒网的输出即相应为

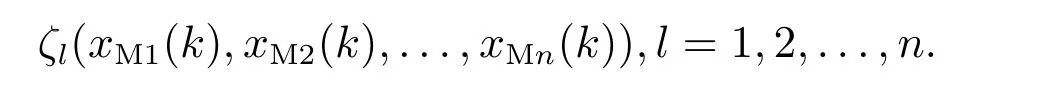
对于非线性时间序列,系统的动力学方程式(6)中取C=(1,0,...,0),即y(k+1)=x1(k+1).将数据重构形成样本集其中样本集输入为

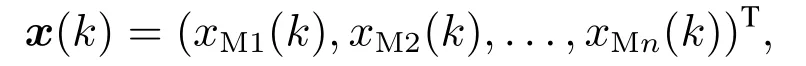
其对应输出为y(k+1).

对于非线性时间序列而言,多维泰勒网输出为

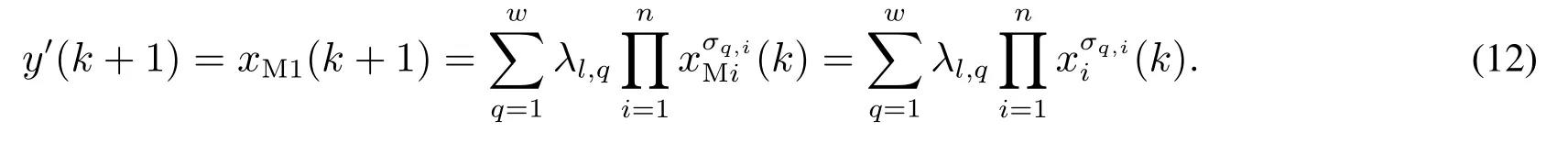
该输出可以采用最小二乘法求解得到各乘积项的权值λ1,q[20],从而可以确定平稳区的模型参数.

3.2 剧变区模型参数求解

采用多维泰勒网方法进行正负反馈交替论模型中平稳区参数的辨识之后,由于数据在剧变期发生剧烈大幅度变化,所以需要根据样本数据进行数据剧烈变化段的正反馈参数辩识,以反映在多维泰勒网的基础上叠加的由于剧变造成的正反馈影响.

系统在不断呈现“平稳→剧变→再平稳→再剧变”的运行过程中,由于能量积累的程度不同而导致在不同剧变期能量爆发的幅度,即状态变量的变化量幅度的不同.从而可根据变化量幅度大小的不同划分出若干个剧变期,即 sdez(Δx1,α1BPσ,α1EPσ,α1BNσ,α1ENσ),σ=1,2,...,µ所对应的第σ个正向(或负向)的等效正反馈的状态变化量起点α1BPσ(或α1BNσ),以及等效正反馈的状态变化量终点α1EPσ(或α1ENσ).具体步骤如下:

步骤1计算各变化量的幅度大小,即Δx1(k)←x1(k)-x1(k-1)；

步骤2比较变化量幅度的大小,即比较Δx1(k)和Δx1(k-1)的幅值的大小,并将该较大的变化量幅度保存为maxΔx1(k)；

步骤3根据maxΔx1(k)值进行稳定区域判断.若maxΔx1(k)较小,且该maxΔx1(k)为数据转折点,即达到波动幅值后,变化幅度不会继续增加而是呈现衰减情况,则处于平稳区.剧变区数据变化与平稳期截然不同.若maxΔx1(k)较大,且当出现较大的maxΔx1(k)值之后,波动幅度若持续增长,即maxΔx1(k)＜maxΔx1(k+1)＜···＜maxΔx1(k+p),则出现正反馈.当变化量幅值增长到某一更大幅值后,出现maxΔx1(k+p)＞maxΔx1(k+p+1)即出现转折,则表明正反馈作用消散,此次能量爆发结束；

步骤 4根据稳定区域判断过程及结果,确定正反馈区a1σsdez(Δx1,α1BPσ,α1EPσ,α1BNσ,α1ENσ)所对应的状态变化量起点α1BPσ或α1BNσ,以及状态变化量终点α1EPσ(或α1ENσ)；

步骤5在确定各正反馈区边界参数之后,对处于各等效正反馈状态变化量起止点之间的序列数据,分别计算各剧变期区域内x1(k+1)与xM1(k+1)的差值,并求取其在各剧变区的算术平均值,即得到各剧变区的平均误差,以获得对应于各等效正反馈区域的参数a1σ,σ=1,2,...,µ.

4 算例仿真

4.1 算例1

在结构工程领域中,诸如高层建筑、大型桥梁等结构,在其长达几十年的服役期中,长期经受着环境的侵蚀、材料的老化以及荷载的变化,这些因素将不可避免地造成建筑结构的损伤累积和抗力衰减,从而导致其抵抗自然灾害的能力下降,甚至出现垮塌,造成巨大的经济损失.

本文模型采用叠加死区函数反映系统状态由于能量爆发造成的正反馈作用,将状态稳定性分离,通过对楼宇、桥梁的监测数据进行采样和分析,可以基于监测数据建立此类系统的动力学方程.这种智能建模方法将对楼宇、桥梁的垮塌灾害加以监控,它的研究将为解决类似具有量变质变现象的复杂工程系统的建模问题提供了一条新颖的途径.

由于目前尚无楼宇或桥梁垮塌过程的实测数据,为便于研究,借助专业有限元分析软件MSC.Marc模拟某九层楼宇在罕遇地震作用下的响应及破坏过程数据,结合破坏过程中量变到质变这一过程,进行基于正负反馈交替论的非线性系统建模.

仿真实验中针对非线性时间序列{x(k)},模型输入向量为x(k)=(x1(k),x2(k),x3(k),x4(k))T,其中各元素采用差分结构

首先进行网络学习,获得平稳区函数

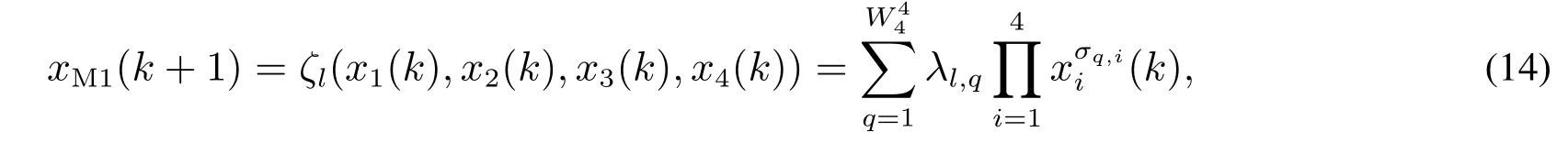
从而得到输出y′(k+1)=xM1(k+1).

然后,按照前述的变化量幅值比较法确定等效正反馈区的起止边界参数,以及正反馈区内求取平均误差的方法,获得函数a11sdez(Δx1(k),α1BP1,α1EP1,α1BN1,α1EN1)的各参数.

如前所述Δx1(k)=x1(k)-x1(k-1)=x2(k),所以该正反馈函数a11sdez(Δx1(k),α1BP1,α1EP1,α1BN1,α1EN1),即为a11sdez(x2(k),α1BP1,α1EP1,α1BN1,α1EN1),从而建立其正负反馈交替论模型,通过式(15)的显性形式对该九层楼宇的动力学特性加以描述,即

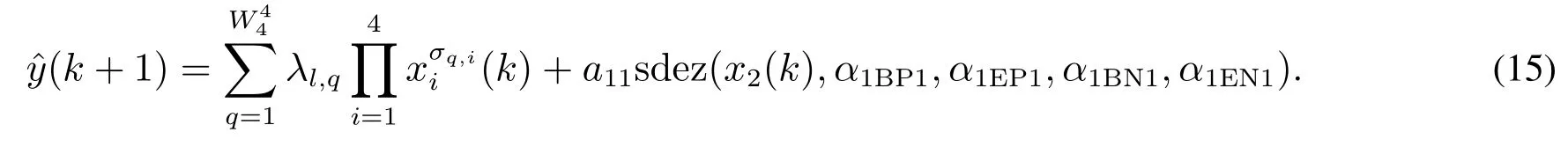
对于建立的模型,需通过测试数据对其模型性能进行评价.在进行性能测试时,采用同地区的另一地震波对该九层楼宇进行振动实验,将实际水平位移响应与式(15)描述的正负反馈交替论模型的每一步预测结果进行对比,对比结果如图4所示.

图4反映了该九层楼宇的最高层(第九层)在超高强度地震波作用下,破坏过程中水平位移数据的正负反馈交替论模型计算结果与实际值的对比情况.该时间序列清晰反映了实验对象在高强度振动下,水平位移由量的积累到产生剧变,最后楼宇垮塌的这一演变过程.

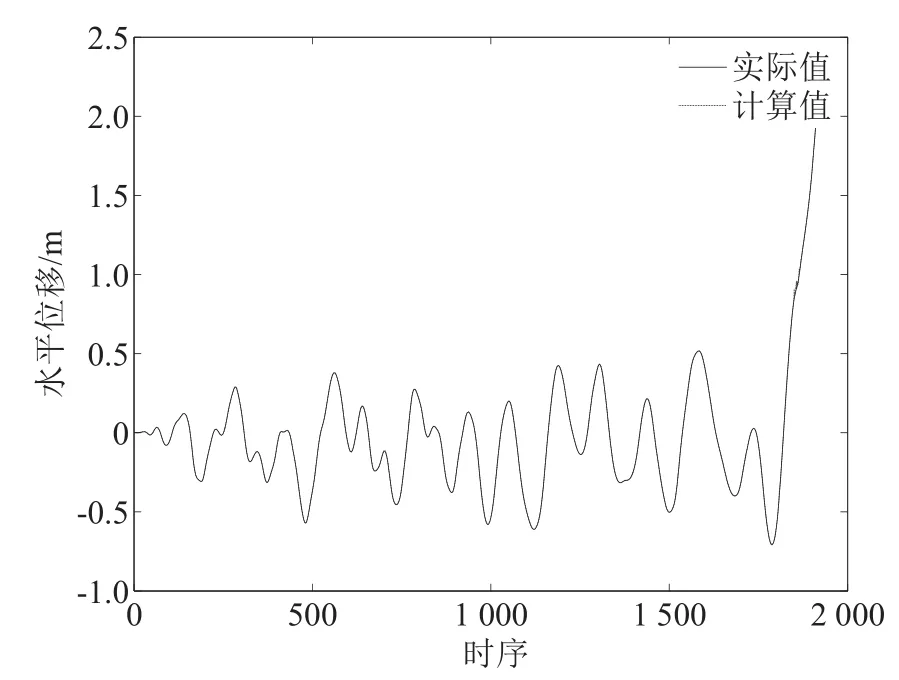
图4 计算结果与实际值对比图Fig.4 Comparison of the calculated results and the actual value

分别对图4中平稳区和剧变区进行局部放大,如图5和图6所示.

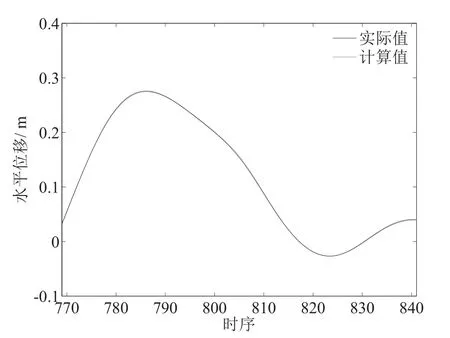
图5 平稳区局部放大Fig.5 Local amplification of stable area

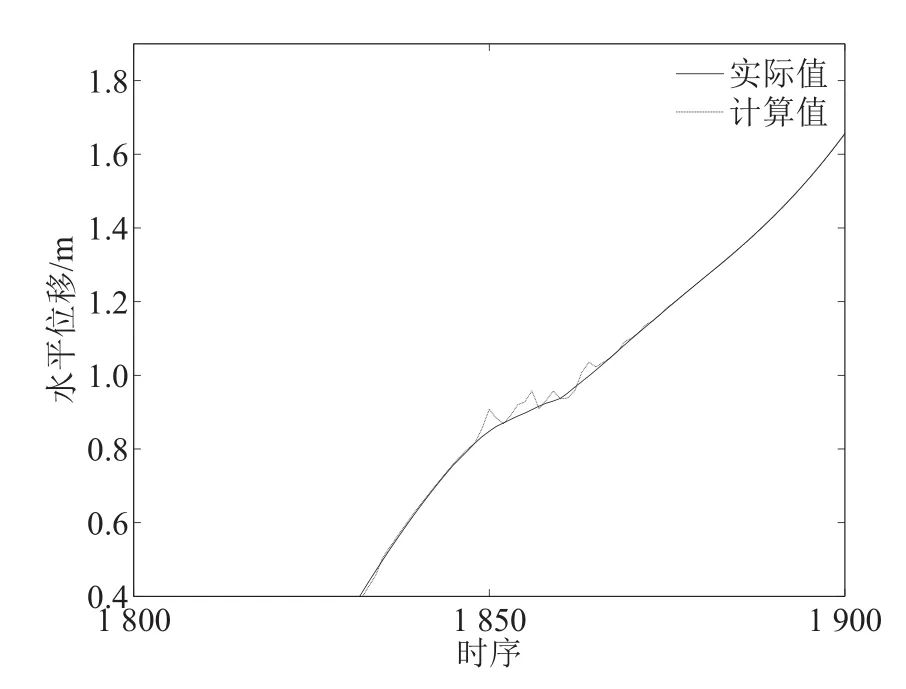
图6 剧变区局部放大Fig.6 Local amplification of revulsion area

从图4以及局部放大的图5和图6可以看出,结合破坏过程中量变到质变这一过程进行的正负反馈交替论模型可以较好地反映该九层楼宇在罕遇地震作用下的响应及破坏过程,是解决具有量变质变现象的复杂工程系统建模问题的一种新途径.

图5反映出平稳区该模型具有很高的预测精度,但在图5所示的剧变区对比图中可以看出,虽然就整个剧变区而言该模型依然具有较好的预测效果,但在局部位置出现了比较明显的误差.分析其主要原因,出现较大误差的区域即为垮塌即将发生时状态产生急剧变化的剧变期,该区的数据变化反映的恰恰是由量变到质变的转变过程,虽然正负反馈交替论模型已经引入了正负反馈对稳定性进行分离,整个剧变区内模型与实际数据可以有较好的吻合,但在分离点处仍存在一定误差.此外,还有一方面原因在于,虽然已将垮塌发生之前,以及垮塌过程中的数据值纳入剧变区函数的训练集,但在频谱存在差异的地震波的振动下,特别是垮塌本身的剧变类型,即便是针对同一建模对象进行模型描述,也会出现个别数据预测精度较差的情况.

为了更充分地反映模型性能,本文将正负反馈交替论模型(本文模型)与未引入状态控制的多维泰勒网模型(MTN模型)、BP神经网络模型(BP模型)以及遗传算法优化的BP神经网络模型(GA-BP模型)进行模型预测效果结果对比,比较结果如表1所示.模型性能评价标准采用预测的均方根误差(RMSE)和相对误差(PERR),其分别定义为

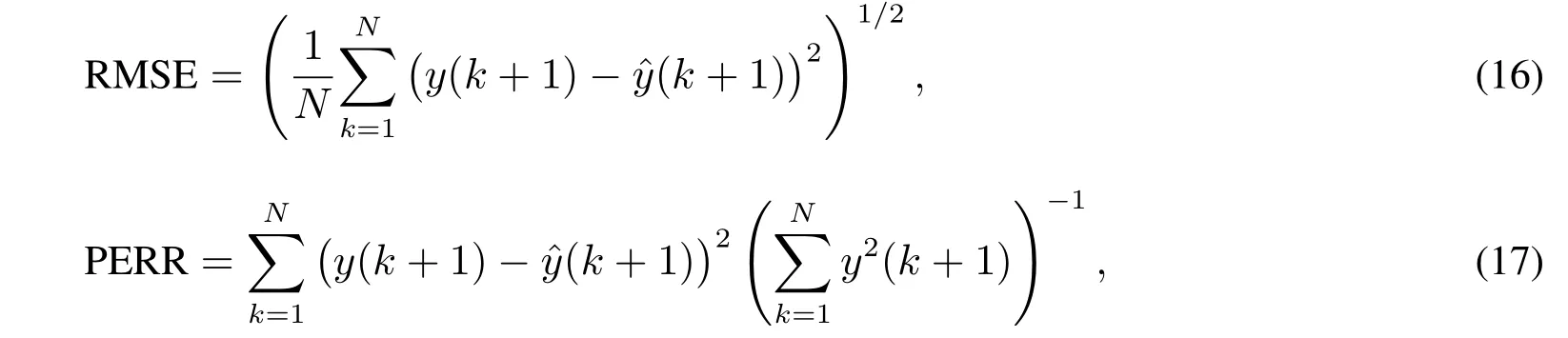
其中N为测试样本容量,y(k+1)为实际值,(k+1)为预测值.

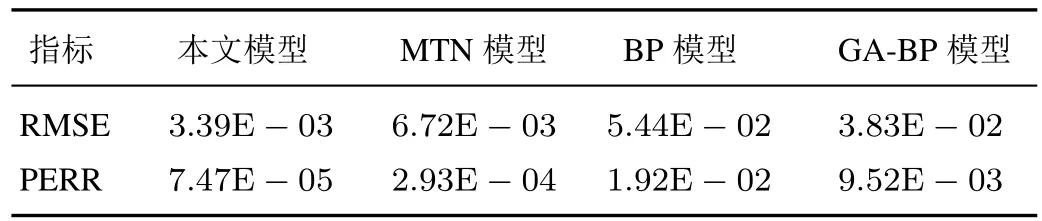
表1 测试数据误差比较Table 1 Comparison of test data errors

从表1可以看出,本文所提正负反馈交替论模型的两项误差指标均优于单纯的多维泰勒网方法、BP神经网络模型以及遗传算法优化后的BP模型.主要原因在于本文模型能够针对具有“平稳→剧变→再平稳→再剧变”变化规律的这类系统,将状态稳定性分离,只在剧变区采用相应等效正反馈补偿,进一步减小了在一般基于数据的建模过程中动态特性改变对平稳区数据的影响.故本文模型精度好于单纯的多维泰勒网模型.又由于本文模型以MTN模型为核心子模型,在充分发挥了其预测精度高的优势的同时,将状态稳定性分离,故其RMSE和PERR这两项指标相较于BP模型和GA-BP模型具有显著优势.

4.2 算例2

水位是关系到水库大坝安全、灌溉调度、蓄水以及泄洪的重要参数.由于水位变化也具有典型的“平稳→剧变→再平稳→再剧变”变化规律,本文根据某水利枢纽每日上午8:00上游水位监测值,采用正负反馈交替论模型进行水位预测研究.利用MATLAB7.0编写正负反馈交替论模型程序,水位预测结果与实际水位值对比如表2所示.

为了更好地反映预测性能,本文将正负反馈交替论模型与多维泰勒网模型(MTN)、BP神经网络模型(BP)、RBF神经网络模型(RBF)水位预测结果进行对比,预测结果的误差统计如表3所示.

由表3可以看出,对于大坝上游水位这种总体变化呈现“平稳→剧变→再平稳→再剧变”这一变化规律的非线性系统,相较于BP模型、RBF模型这样的神经网络模型以及MTN模型,本文所提出的正负反馈交替论模型在预测精度方面具有更好的优势.

从上述仿真实验可以看出,本文方法所建立的模型具有更高精度,能更准确地反映系统状态的变化规律,特别是针对剧烈变化的情况具有更好的优势.此外,本文所提模型通过引入等效正负反馈对系统的稳定区及不稳定区进行划分,能以动态数学模型的形式显性表示历史观测数据对未来数据的影响,从动力学模型的角度探讨了系统变化规律的定量表达.这也是时间序列建模方法的一个新的研究与尝试.

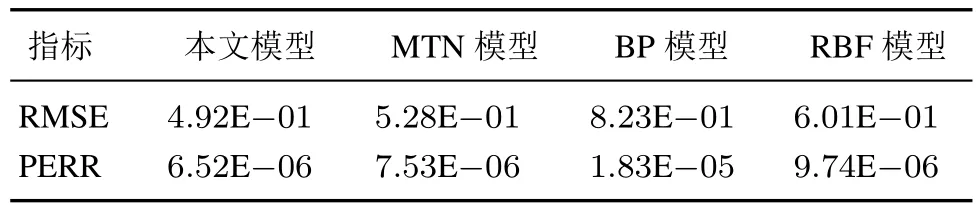
表3 误差统计Table 3 Error statistics

5 结束语

本文将正负反馈的思想与系统状态呈现“平稳→剧变→再平稳→再剧变”的过程相结合,提出了一种新型的描述此类系统演变规律的正负反馈交替论模型.该模型根据时间序列中数据的变化情况,引入正负反馈概念,将稳定性分离,在采用多维泰勒网方法进行模型参数辨识的基础上,对呈现不同动态特性的区域分别进行稳定区和剧变区的参数辨识,建立系统模型.该模型能够在系统机理不明的情况下,建立系统的动力学方程,以动态数学模型的形式表述具有“平稳→剧变→再平稳→再剧变”状态演化规律的这一类系统.由于模型将稳定性分离,对数据的变化添加了正负反馈的作用,进一步提高了建模精度,且算法实现方便.最后采用楼宇在罕遇地震作用下的响应及破坏过程数据,以及大型水利枢纽的水位监测数据作为非线性时间序列,进行基于正负反馈交替论的非线性系统建模及预测实验仿真,结果表明本文所提方法的有效性.