BDS的RAIM算法设计与实现

谢金石，辛 洁，2，郭 睿，2，王冬霞，2

(1.北京卫星导航中心，北京 100094；2.大地测量与地球动力学国家重点实验室，武汉 430077)

0 引言

完好性监测能够对系统存在的、影响定位精度的故障进行有效检测和排除[1]，是检验卫星导航定位服务品质的有效有段。当前3大完好性监测方法[2]为：1)外部增强方法，例如广域增强系统(wide area augmentation system，WAAS)、局域增强系统(local area augmentation system，LAAS)等在向用户播发误差改正数的同时也给出改正数的完好性信息[3]；2)接收机自主完好性监测(receiver autonomous integrity monitoring，RAIM)方法，利用导航卫星的冗余信息，实现多个导航解的一致性检验，以达到完好性监测的目的[4-6]；3)系统基本完好性监测和卫星自主完好性监测[7-8]。

目前，国内对全球定位系统(global positioning system，GPS)下的RAIM算法进行了广泛深入的研究[9-11]，得到一系列有价值的研究成果；而我国拥有自主知识产权的北斗卫星导航系统(BeiDou navigation satellite system，BDS)采用的是混合星座，因此基于BDS条件下的RAIM算法具有一定的特殊性。

本文通过介绍RAIM算法中故障检测和故障识别的基本原理，分析区域导航条件下RAIM算法的可用性，以及截止高度角、可视卫星数、精度因子值(dilution of precision，DOP)等因素对RAIM可用性的影响，得出中国区域内RAIM算法的中断时间，为相关研究提供参考。

1 RAIM算法分析

RAIM算法是一种以粗差的探测和分离理论为基础的算法，致力于判断卫星是否存在故障，并查找星座中的故障星。当观测星数大于4颗时，可以进行故障检测(fault detection，FD)；当观测星数大于5颗时，可以进行故障识别(fault identification，FI)。

1.1 基于残差平方和的故障检测算法

首先建立卫星导航的伪距观测模型为

y=Ax+ε。

(1)

式中：y为观测伪距与近似计算伪距差值，y∈Rn×1，R为矩阵符号，n为可视星数目；A为由各卫星到用户接收机的方向余弦向量构成的线性化矩阵，A∈Rn×4；x为用户接收机的真实位置、钟差，x∈R4×1；ε为各卫星的伪距测量误差，ε∈Rn×1。

通常需要对模型中所有观测量进行等权处理。向量x的最小二乘解

(2)

伪距残差向量为

v=Qvε。

(3)

式中：v为各卫星的伪距残差向量；Qv=I-A(ATA)AT为伪距残差向量。

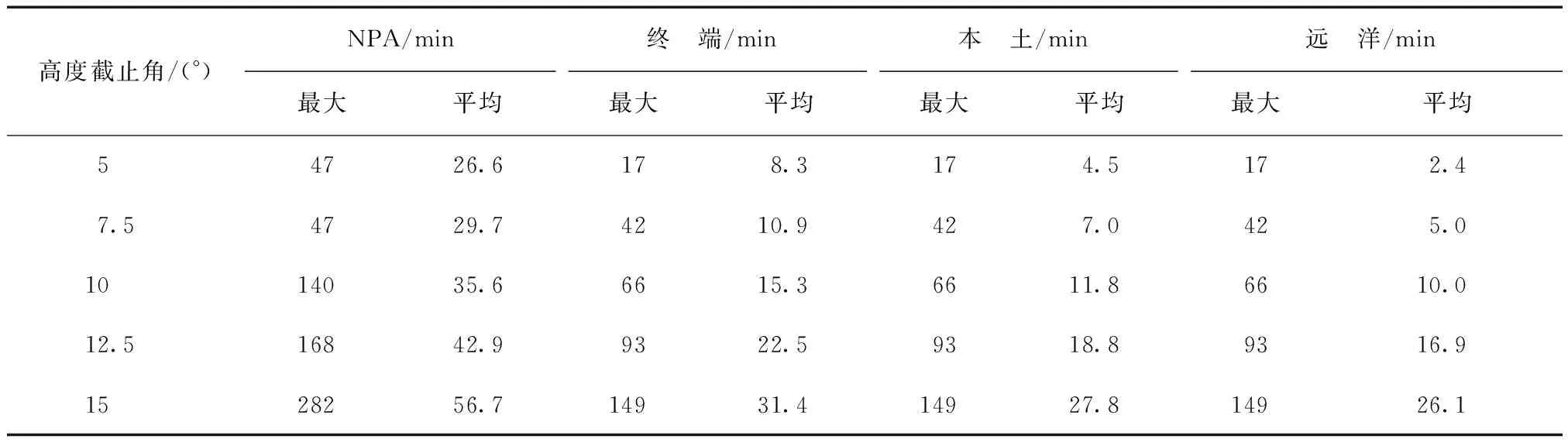
验后单位权中误差

(4)

式中SSE=vTv为残差平方和。

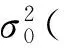
若系统处于正常检测状态且无伪距故障，却出现检测告警，则为误警。误警概率

(5)

由此可以看出，可视星相同条件下，误警概率越低，检测的门限值将会越大，从而降低故障检测精度；误警概率相同条件下，可视星个数越多，检测门限值越小，则故障检测精度越高，更有利于故障检测。

1.2 故障检测的完好性保证算法

卫星几何分布会影响RAIM检测结果。当卫星几何条件不佳时，可能会出现导致漏检的现象；故在进行故障检测之前，需先判定卫星几何条件是否满足最大漏检率需求，给出完好性算法保证。

(6)

卫星几何是否可用通常采用水平/垂直定位误差保护限值HPL和VPL来确定，既能保证系统的完好性，又反映了系统卫星几何的可用性，具体计算公式为：

(7)

(8)

式中：δHDOPmax为最大平面精度因子变化；δVDOPmax为最大垂直精度因子变化。

通过HPL和水平告警限值HAL、VPL和垂直告警限值VAL间的比较，可以得出RAIM算法的完好性保证，进而得到RAIM算法的可用性。

1.3 基于残差元素的故障识别算法

对于最小二乘残差矢量构造的统计量，可根据其服从的某种分布给定显著水平，进而通过统计量的检验来判断某残差是否存在粗差。根据残差和观测误差的关系式，则设第i颗卫星检验统计量

(9)

式中：Vi为第i颗卫星的伪距残差向量；QVii为伪距残差向量主对角线上的元素。

依据统计分析理论，对统计量di进行如下假设：无故障概率H0：E(ε)=0，则di遵从标准正态分布，记为di～N(0，1)；有故障概率H1：E(ε)≠0，则di遵从参数为σi和1的正态分布，记为di～N(δi，1)，其中δi为统计量偏移参数。

若第i颗卫星的伪距偏差为bi，则

(10)

通过以上检验统计量可知，n颗可视星共得到n个检验统计量。若总体误警概率为PFA，则每个检验统计量的误警概率为PFA/n，则有

(11)

对于每个检验统计量di，分别需与检测限值Td进行比较，即di>Td时，则表明第i颗卫星可能存在故障。

由此可以看出：在可视星个数相同的条件下，误警概率越低，检测门限值越大，故障灵敏度越差，从而降低了故障识别精度；在误警概率相同的条件下，可视星个数越多，检测门限值也越大，更不利于故障的识别。这与FD的关系情况恰好相反。

1.4 故障识别的完好性保证算法

在故障识别之前，同样要判定卫星几何条件是否满足故障识别的需要，以判断算法的可用性，给出完好性算法保证。

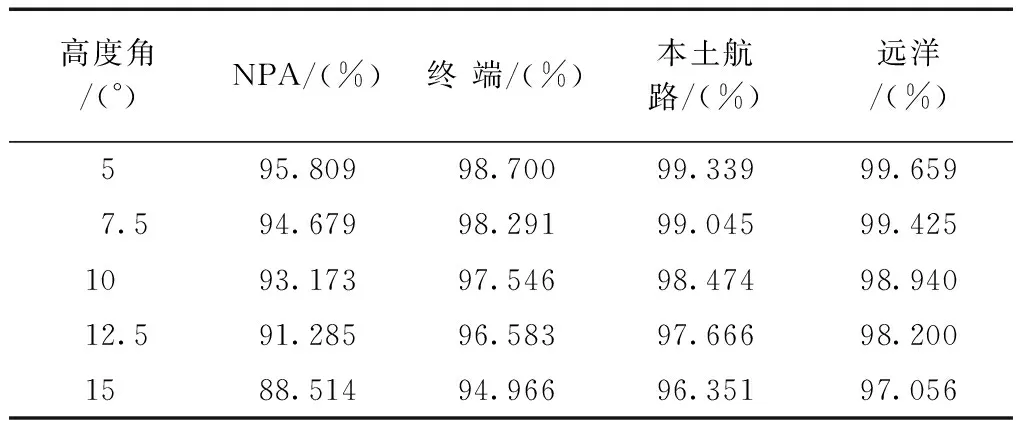
若存在卫星故障，检测限值Td应小于检测统计量di。若di

(12)

式中δ为统计量偏移参数。与故障检测的完好性保证算法类似，故障识别完好性也需通过计算水平和垂直定位误差保护值的大小进行判断，其计算公式为：

HPL=δHDOPmax×σ0×σ；

(13)

VPL=δVDOPmax×σ0×σ。

(14)

然后分别与水平定位误差限值HAL、垂直定位误差VPL进行比较，得到RAIM故障识别算法的可用性。

由此可以看出：在漏警率和可视星个数相同的条件下，误警率越低，非中心化参数越大，对应的HPL值也越大，必然导致RAIM故障识别的可用性降低；在误警率和可视星个数相同的条件下，漏警率越低，非中心化参数越大，对应的HPL值也越大，也会引起RAIM故障识别的可用性降低；在RAIM故障识别的可用性一定的情况下，漏警率和误警率是自相矛盾的，难以同时满足低漏警率和低误警率。

2 实验与结果分析

为了分析区域导航系统下RAIM算法的可用性，仿真中对中国及周边区域(75°E～135°E，10°N～55°N)进行了格网化，得到108个格网点，具体格网化结果如图1所示。

在仿真计算中，首先采用STK软件模拟生成24 h卫星星历数据，同时生成中国区域和部分亚太地区内格网点在地固系中的坐标，以1 min的采样间隔，共得到1 440个观测时刻。等效测距误差取5 m，非精密进近(non precise approach，NPA)、终端、本土和远洋4个飞行阶段的水平定位告警限值分别取556、1 852、3 704和7 408 m。当区域导航系统作为唯一导航时，在4个飞行阶段中，误警率取1×10-7/采样个数，漏警率取0.001。

2.1 截止高度角对可用性的影响

卫星截止高度角E不但影响可视卫星个数，还影响观测的卫星几何条件。将卫星截止高度角依次设为5°、7.5°、10°、12.5°和15°，分析NPA、终端、本土和远洋4个飞行阶段故障检测和故障识别的可用性结果(如表1、表2所示)。

表1 FD可用性统计结果

表2 FI可用性统计结果

根据表中得到的结果可知：

1)对于4个航行阶段，高度截止角越大，可视星个数越少，卫星几何结构越差，对基于RAIM算法的故障检测和故障识别可用性愈低；

2)故障识别的可用性要低于故障检测，该关系不受截止高度角和飞行阶段等因素的影响；

3)在NPA航行阶段，RAIM算法可用性对卫星截止高度角更加灵敏，其他3个阶段中RAIM算法对卫星截止高度角的灵敏度相当。

2.2 可见卫星数对可用性的影响

通过对NPA、终端、本土和远洋4个阶段超限结果的统计，分析可见卫星数与可用性之间的关系。表3和表4分别给出5°和10°高度角下可视卫星个数与RAIM故障检测和识别算法可用性之间的关系。

表3 E=5°可视卫星个数与可用性

表4 E=10°可视卫星个数与可用性

从表的结果可以得到如下结论：

1)在10°截止高度角左右，区域导航系统在中国区域内的可视卫星个数以7～8颗为主；

2)随着可视星个数的增加，卫星观测几何条件得到改善，进而提高RAIM算法的可用性；

3)可视星个数相同条件下，故障识别的可用性要低于故障检测的可用性；

4)当可视星个数大于8时，故障检测和排除算法的可用性达到100 %。

2.3 DOP值对可用性的影响

当前卫星几何条件可通过DOP值来反映，因此DOP值对可用性也存在间接影响。如图2、图3所示，为分析DOP值因素对RAIM算法可用性的影响，可在所有历元点计算所有格网点的可用性情况及相应历元点的几何精度因子(geometric dilution of precision，GDOP)和水平精度因子(horizontal dilution of precision，HDOP)值，以分析卫星观测条件对可用性的影响。

从图中可知：

1)整体来看，相同截止高度角条件下，GDOP

值对FD和FI可用性的影响大致相同，当GDOP∈(0,3)时，FDI可用性较高；但GDOP与可用性之间的规律性并不明显，即并不是GDOP值越大，可用性越差，这是因为FDI可用性的最直接影响因素是δHDOPmax，不过当GDOP值大于7时，FD和FI的可用性逐渐接近；当GDOP值相同时，FD的可用性要大于FI的可用性。

2)整体来看，相同截止高度角条件下，HDOP值对FD和FI可用性的影响大致相同，当HDOP∈(0,3)时，FDI可用性较高；但HDOP与可用性之间的规律性并不明显，即并不是HDOP值越大，可用性越差，这是因为FI可用性的最直接影响因素是δHDOPmax，不过当HDOP值大于6时，FI算法的可用性接近于0；当HDOP值相同时，FD的可用性要大于FI的可用性。

2.4 RAIM算法的中断时间

依据前面仿真计算中的可用结果，对中国区域内108个格网点的RAIM算法中断时间进行统计分析，分别计算得到最大中断时间和平均中断时间。

在中国区域内，RAIM算法的可用性存在差异，故障检测和故障识别算法的中断时间也不同。下面给出不同飞行阶段、不同高度截止角条件下故障检测和故障识别算法的最大中断时间和平均中断时间。

表5～表6、图4～图5是在中国区域内，NPA飞行阶段中不同截止高度角条件下的区域内格网点FD和FI最大中断时间统计情况。

表5 故障检测中断时间统计结果

表6 故障识别中断时间统计结果

从表1～表6、图1～图5可知：

1)从整体而言：高度截止角越大，RAIM算法中断时间越长；RAIM算法最大中断时间按照NPA、终端、本土和远洋顺序依次减小；相同高度角和飞行阶段条件下，故障识别最大中断时间要大于故障检测最大中断时间。

2)在低高度截止角条件下，中国区域内RAIM算法最大中断时间变化不大；但随着高度截止角越大，观测条件不佳，边缘部分最大中断时间要高于中部和低纬地区。

3)在中国区域内的低纬地区，区域导航系统能够很好满足RAIM算法的可靠性要求，保障接收机自主完好性监测的要求。

3 结束语

基于RAIM故障检测和故障识别及其完好性保证算法的原理，本文通过仿真分析不同截止高度角、可见卫星数和DOP值下RAIM的可用性，得出分析结果如下：

1)故障识别可用性要低于故障检测；

2)高度截止角越大，可视卫星个数越少，RAIM可用性都会越低，5°高度角时NPA阶段FD可用性为95.809 %，FI可用性为95.608 %；

3)随着可视星个数的增加，RAIM可用性越高，若可视星数大于8，则FD和FI可用性达到100 %；

4)相同高度角条件下，GDOP值和HDOP值对FD和FI可用性的影响趋势相同，但规律性并不明显；

5)RAIM中断时间与高度角、飞行阶段有关系，相同高度角和飞行阶段条件下，FI最大中断时间要大于FD；

6)在低高度截止角条件下，中国区域内RAIM算法最大中断时间变化不大，但随着高度截止角越大，观测条件不佳，边缘部分最大中断时间要高于中部和低纬地区，在低纬地区，区域导航系统能够很好地满足RAIM的可靠性要求。

[1] 吕小平.发展我国的GNSS完好性监测系统(一)[J].空中交通管理，2004，20(3)：6-10.

[2] 张倩倩.新型RAIM算法的研究及其应用[D].郑州：信息工程大学，2015.

[3] 陈金平.GPS完好性增强研究[D].郑州：信息工程大学，2001.

[4] 郭睿，唐波，陈刘成.GPS系统下RAIM算法可用性及结果分析[J].海洋测绘，2007，27(6)：40-45.

[5] 郭睿，韩春好，冯平平，等.接收机自主完好性监测的算法分析[J].测绘工程，2008，17(2)：34-38.

[6] 郭睿，郑勇，杜兰.GPS和Galileo系统下RAIM算法可用性分析[J].测绘科学技术学报，2006，23(6)：448-450.

[7] 王淑芳，孙妍.卫星自主完好性监测技术[J].测绘科学技术学报，2005，22(4)：266-268.

[8] 范媚君.卫星导航系统完好性模型与算法研究[D].郑州：信息工程大学，2013.

[9] 李征航，黄劲松.GPS测量与数据处理[M].武汉：武汉大学出版社，2005.

[10] 邵炳军.GPS-Galileo组合导航卫星系统研究[D].南京：南京航空航天大学，2009.

[11] 郭睿，张健铤，冯平平，等.伪卫星增强下的RAIM算法可用性及性能分析[J].天文学进展，2009，27(1)：89-97.