重点突围 纵向推进 横向拓展

高玉红

[摘 要]小学数学中的概念看似简单，但要明确内涵、界定外延，让学生透视概念本质却不容易。如人教版教材五年级下册“分数的意义”，要使学生充分透彻地理解分数的意义，就必须进行拓展。

[关键词]突围；分数；内涵；外延；意义；单位“1”

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2018）02-0040-01

对于代表数量的“1”，学生有着丰富的认知。如，学生知道1件物品可以用数字“1”来概括其数量意义。这种认知观念根深蒂固，因此，要将具体的“1”扩延到抽象的单位“1”，有一定难度。教师应如何突破这一难点呢？

一、全力突围——积极建构单位“1”

总览教材，分数知识的排布具有梯度性。在五年级“分数的意义”中，重点是探讨“均分单位‘1，取其中若干份时如何用分数表示”。显然，学生能否正确理解单位“1”的含义是教学的关键。基于此，笔者将个体“1”到集群“1”的扩延作为重头戏。

【片段1】

师：生活中，1用来表示什么呢？

生1：一个足球或一只狗。

生2：一副乒乓球拍、一打羽毛球也可以用1来表示。

师：你能解释一下吗？

生2：一副乒乓球拍有2个拍，一打羽毛球有12个，它们都是是一个整体，都可以用“1”表示。

师：这里的“1”和以前的“1”有什么不一样？

生3：以前的“1”表示单个物体，这里的“1”是一个集群，包含很多个体。

师：一个物体或多个物体，都可以看成“1”，我们把多个物体组成的整体称为单位“1”。

学生通过自己举例、质疑、探讨、领悟，自然地引出单位“1”的新概念，并通过丰富而恰当的举例来构建单位“1”的稳固表象。但教师并未满足于此，而是趁热打铁，借助实践操作，增进学生对单位“1”的认识。

【片段2】

师：你能绘图表示1/4吗？

生1：如图，画4个一样的方块，其中黑色的那块就表示1/4。

生2：应该把4个方块圈起来，表示一个整体，再切分。

师：不圈起来能够表示单位“1”吗？

随后，教师画圈（如下图），这时学生深刻意识到：要表示整体的1/4，必须先将整体体现出来，然后才能作为单位“1”均分。

二、纵向推进——深刻理解分数意义

除了构建单位“1”的意义，还应借助不同情境，通过多层教学从求同与求异两个方面向纵深推进。

【片段3】

生1：把4张桌子视为一个整体，均分成4份，其中一份就是1/4。

生2：把8把椅子视为一个整体，均分成4份，其中一份就是1/4。

师：为什么都能用1/4来表示？

生3：它们有一个共性，就是单位“1”都被均分成4份，所占份数都是其中的1份。

求同比较能迅速突出分数的本質属性，加深学生对分数的认识。

【片段4】

师：这里有8个方块，请表示出你喜欢的分数。

生1：我把它等分成2份，其中的1份是1/2。

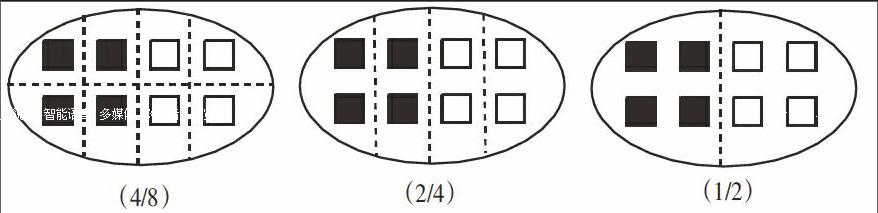
师：观察下面三幅图，你有什么发现？

生2：涂色的方块数量数相等，却用不同的分数表示。

学生在创造分数的过程中进行求异比较，思考为什么对于同一个整的同一部分，却能用不同的分数表示，进一步认识单位“1”，也进一步明白：分数代表部分与总体的比例关系。

三、横向延展——分数意义外延的扩充

学生掌握了分数的本质含义后，要让学生将分数归并到等数域的大背景中去，使学生知晓分数也能表示出数目大小。

【片段5】

师：观察下图，你能找出1/4和3/4在哪里吗？

生：把0和1之间的线段视为单位“1”，将其分成4等份，第一个节点就是1/4，第三个节点就是3/4。

如果到此就鸣金收兵，学生会误认为分数都是比1小的数，对分数形成错误的认知。因此，教师还应该追问：“数轴上1和2之间的其他点是否也能用分数表示呢？”这样学生经过探究就会知道分数可以大于1。同时，学生也能明白分数也可以表示具体的数量，从而完善学生对数的认识。

（责编 吴美玲）endprint