某高层复合桩基础数值分析

汪亚建

(厦门新区建筑设计院有限公司 福建厦门 361012)

0 引言

厦门新景·七星公馆项目采用两阶段变刚度复合桩基础新技术。本文通过七星公馆项目，详细介绍两阶段变刚度复合桩基在解决端承型桩实现桩土共同作用[1]以及特殊地质条件下建造高层建筑等方面的应用，并采用ABAQUS进行数值模拟，验证了两阶段变刚度复合桩基设计的合理性。

1 两阶段变刚度复合桩基础工作机理

两阶段变刚度复合桩基础，通过在端承桩顶部安装变形调节装置，将端承型桩复合桩基的工作状态分为两个阶段，在不同阶段，桩基础的刚度大小不同，亦即复合桩基础的刚度大小不同。

第一阶段为“小刚度”阶段，端承型桩顶部设置变形调节装置，在上部荷载作用下，变形调节装置产生竖向变形，使端承桩的刚度弱化，端承桩和地基土可以协调变形共同工作，形成广义的复合桩基受力机制[2]。为了充分利用地基土的承载力，可以通过理论分析，将端承桩的刚度调节到某一较小的刚度水平，此时上部荷载主要由地基土承担，该阶段为地基土主要承载阶段。第一阶段复合桩基础的沉降机理类似于天然地基基础，沉降量较大。

第二阶段为“大刚度”阶段，该阶段地基土承担的荷载已经接近或达到设计允许值，或者复合桩基的变形量已不允许地基土继续承载。这时，将变形调节装置的空腔采用高强材料填充密实(简称“注浆”)，待空腔内填充材料的强度达到设计要求后，即端承桩的竖向刚度达到设计要求的大刚度水平。后续增加的荷载主要由端承桩来承担，地基土承担的荷载基本维持在第一阶段的水平或者略有增加，该阶段为端承桩主要承载阶段。第二阶段复合桩基础的沉降机理，类似于常规端承型桩基础，沉降量很小。

从最终受力状态出发，两阶段变刚度复合桩基础实现了地基土和端承型桩共同作用的工作机理，形成广义的复合桩基础的概念，为端承型桩在复合桩基础领域的应用提供了新的思路，如图1所示。

图1 两阶段变刚度桩基础示意

2 工程概况

“新景·七星公馆”项目位于厦门市七星路西侧，体育路北侧，总建筑面积为148 439m2，该工程设两层地下室(地下一层为敞开店面，地下二层全埋)，地上由1#～5#楼高层住宅及部分商业组成。其中2#楼地上37层，建筑高度115.0m，采用剪力墙结构，其标准层平面图、剖面图及效果图如图2所示。

图2 标准层平面图、剖面图及效果图

根据地勘报告，该场地土层自地面以下依次为杂填土、粉质粘土、残积土、全风化花岗岩、散体状强风化、碎块状强风化花岗岩、中风化花岗岩。

该场地土层有以下几个特点：

(1)各土层厚薄不均，土层面标高起伏较大，场地自北向南基岩埋深逐步加深。场地北半部分，基岩埋藏较浅，基坑开挖后，底板底面凝灰岩残积土到中风化花岗岩(凝灰岩)各类土层均有揭示。场地南半部分(1#、2#楼)，残积土层、全风化、强风化层较厚，基岩埋藏较深。基坑开挖后，底板底面均为残积土层。

(2)根据钻探揭示：部分钻孔在残积土层和强风化岩层中存在微风化花岗岩孤石，遇孤石的钻孔占总孔数的20%。

3 模型建立与结果分析

利用有限元软件ABAQUS对七星公馆项目2#楼高层住宅楼建立三维有限元数值模型。本节分别从建筑物的沉降、基底土应力、桩顶反力、桩土荷载分担比以及桩侧负摩阻力等方面对两阶段变刚度复合桩基的工作机理进行分析。

3.1 模型建立

3.1.1模型的简化

为了便于对2#楼主楼结构进行有限元软件建模，适当的简化主体结构[3]，具体如下：

采用壳单元(shell)对剪力墙、楼层板进行模拟，采用梁单元(beam)对梁进行模拟。

采用实体单元(solid)对筏板进行模拟，厚度2500mm，由于变形调节装置布置于主楼下基础顶，筏板平面尺寸根据主楼下桩基础外轮廓线外扩约2.5m确定。

剪力墙、楼板、梁等构件，本构件关系为理想线弹性。

采用实体单元(solid)模拟基桩，直径1.1m，桩长30.850m，本构关系为理想线弹性。

采用两套共节点的实体单元(solid)来模拟模型中变形调节装置。一种材料属性是弹簧单元，另外一种材料属性是混凝土单元。采用“追踪单元”方法来实现混凝土属性单元的连续性零应力零应变状态激活。

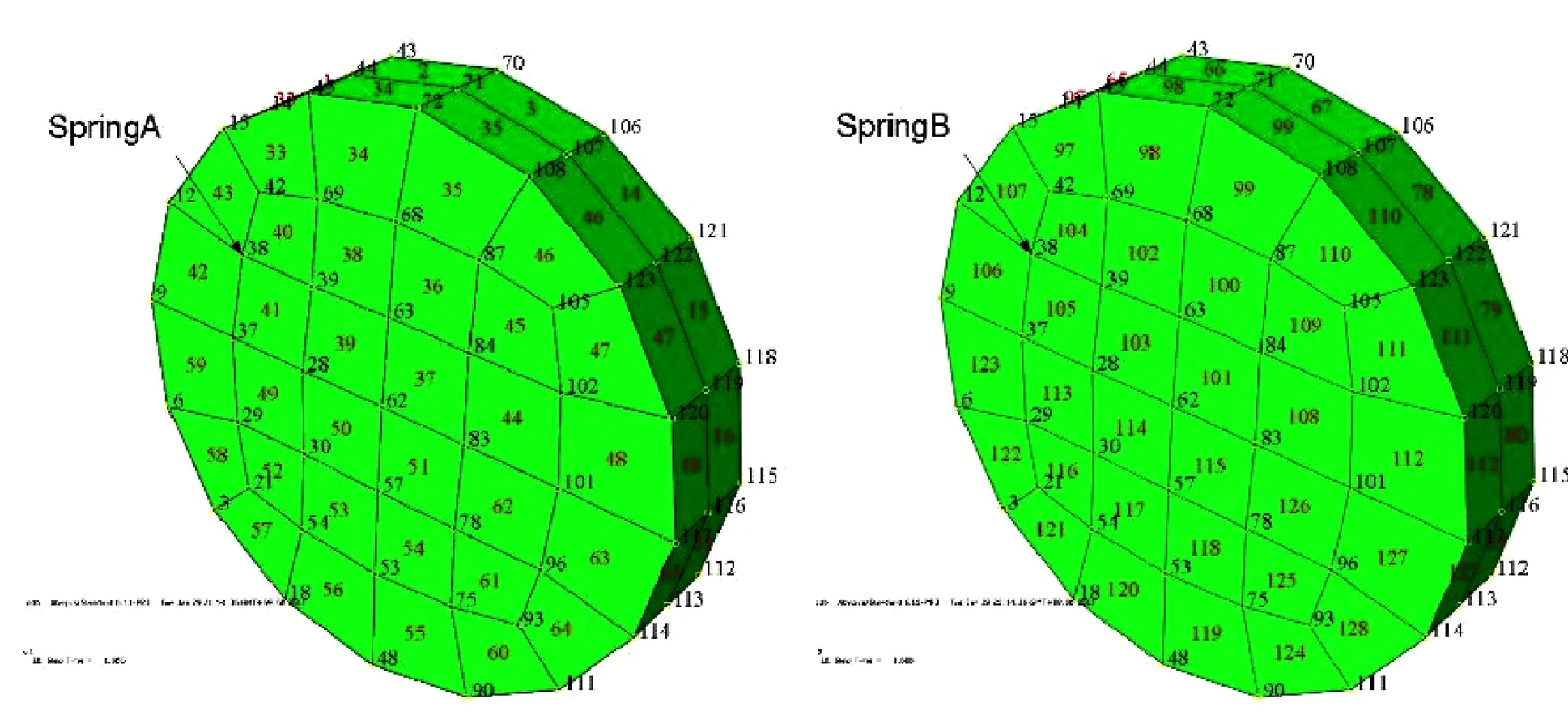
图3 变形调节装置单元

具体做法：如图3所示，创建两个实体SpringA和SpringB，两个实体有完全相同的网格，将SpringA和SpringB合并成一个新的实体SpringAB。生成实体SpringAB时将所有重合节点合并，保留所有重合的单元。这样SpringAB就具有一组节点，但有两组单元。一组节点保证了钝化或者激活单元时，初始位置的连续性；而两组单元可以使变形调节装置具备弹簧的属性和混凝土属性，在不同阶段，根据需要进行激活和钝化处理，从而实现了变形调节装置在ABAQUS中的模拟[4]。

图4 数值计算整体模型示意图

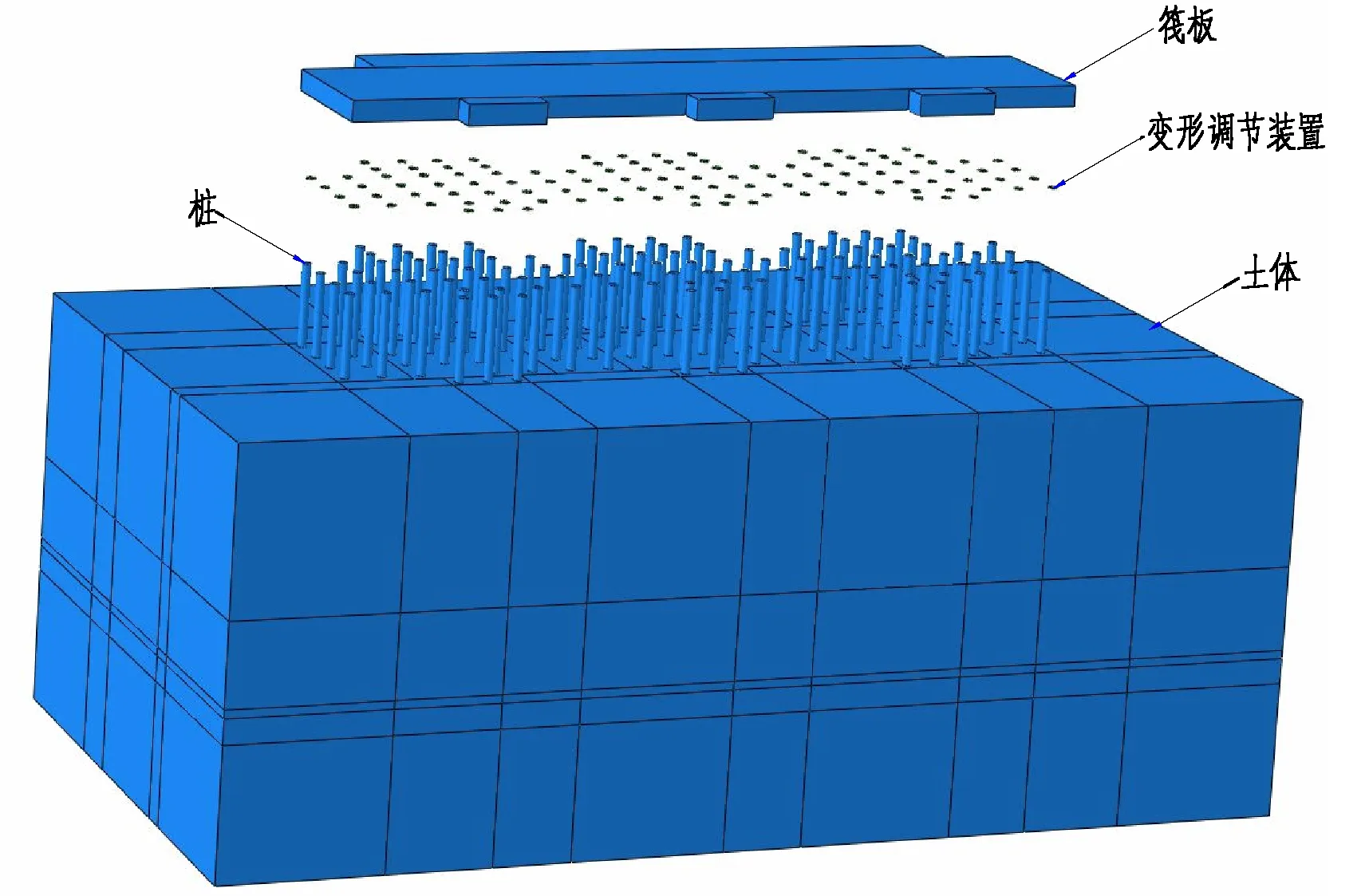
图5 基础模型示意图

考虑到数值模拟的边界影响，土体计算影响区域取建筑基础底板外边线往外扩约20m，土体厚度取桩底向下19m，土体尺寸为131.2m×67.45m×50m，如图4～图5所示。根据该工程地质勘查报告，模型中基础底板以下分别为⑥残积土(20m)、⑦全风化花岗岩(10m)、⑧强风化花岗岩(20m)。其中，⑥残积土用莫尔-库伦模型模拟理想弹塑性本构关系，⑦全风化花岗岩，⑧强风化花岗岩用线弹性型模拟理想弹性本构关系[5]。桩端进入持力层⑧强风化花岗岩1m。

3.1.2有关参数选取

依据七星公馆现有的地质勘察报告和上部结构的设计文件，对建筑数值模型中的各部件赋予相应的材料参数[6]，整个模型主要包括上部结构的楼板、梁、剪力墙，地基土层以及桩基础，具体材料参数[7]如表1所示。

表1 数值模型各部件的材料参数

3.1.3加载方式

为了模拟模型加载前土体的初始状态，模型首先进行地应力平衡。所谓地应力平衡，是给土体施加重力前先为土体定义一个初始应力场，将这个应力分布人为的定义给土体，使其与将施加的土体重力能够平衡，而将土体因自重产生的变形缩小到可以接受的程度(小于10-5mm)，以此来模拟模型加载前土体的初始状态。

建立数值计算模型后，进行地基基础的应力和沉降分析前需要加载。为保证与工程实际一致，通过给上部建筑结构加重力实现加载。分12个分析步进行，每个分析步采用线性加载。

为模拟施工过程，加载过程分12个分析步进行加载。具体加载过程如表2所示。

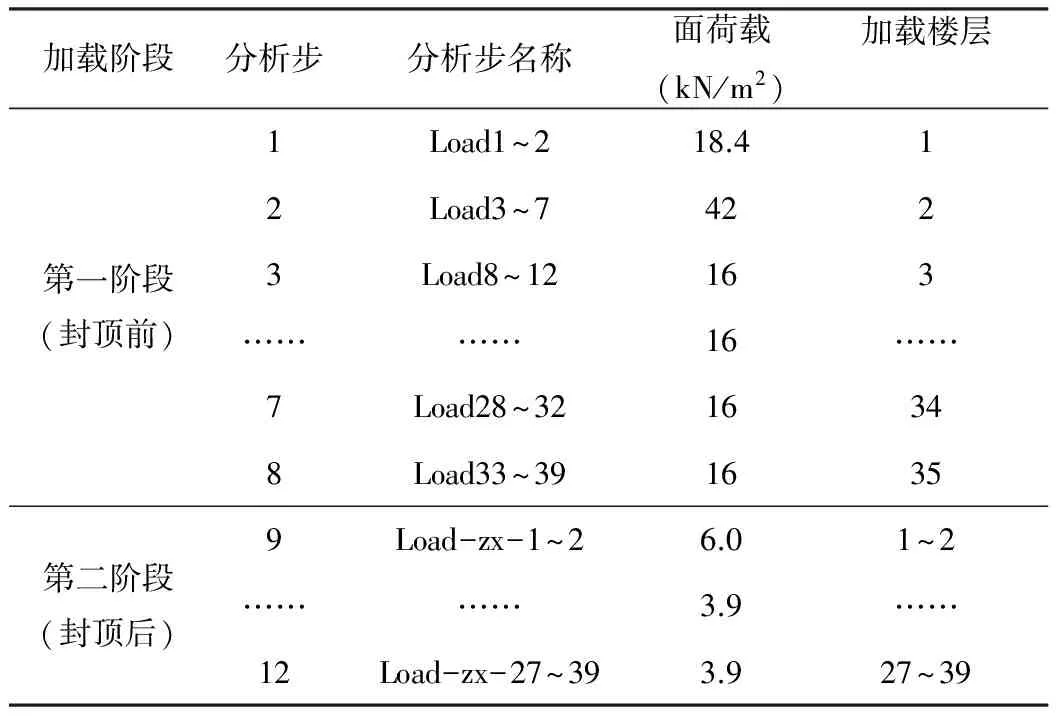
表2 上部结构加载

3.2 结果分析

3.2.1建筑物沉降

图6为地基土沉降剖面云图。桩顶设置调节装置后，主体结构整体沉降分布呈中间大、周围小的“碟形”沉降。由图7可知，第一阶段基础沉降随荷载线性增长，加载主要由土体承担上部荷载，沉降达到75.8mm。此时，建筑物荷载约为设计总荷载的80%左右。建筑封顶至加载结束，建筑物的最终沉降约为84.8mm左右。基础沉降呈现较明显的两阶段特征。

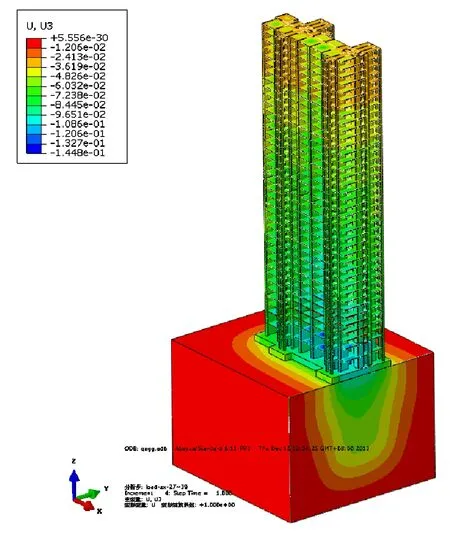
图6 沉降剖面示意图

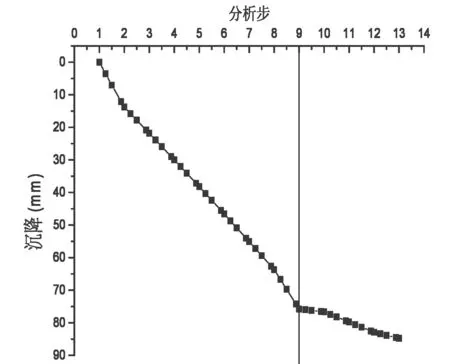
图7 基础沉降

3.2.2基底土应力

为对比实测数据，分析筏板底部地基土应力分布情况，根据土压力盒布置路径提取筏板底部地基土的竖向土应力(S33)，如图8所示。

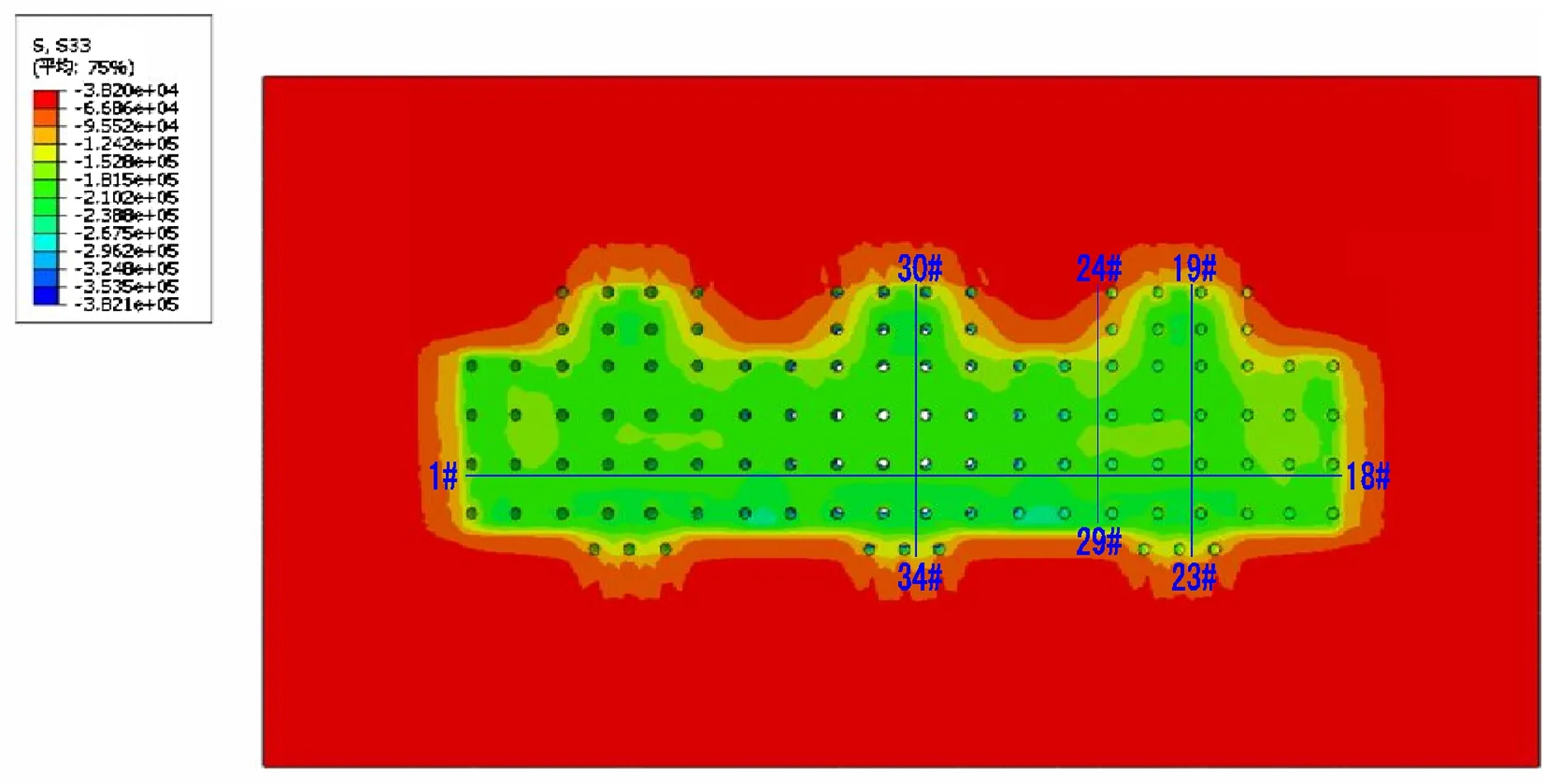
图8 基底土应力分布示意图

图9～图12为土应力沿路径1～4分布情况。加载初期，土应力分布比较均匀，筏板底土反力呈线性增大，并于“注浆”后开始逐渐稳定，最终趋于收敛。

路径1沿筏板基础纵向全长布置。从图8可以看出，最大土应力出现在电梯井附近。同时，我们也注意到，路径1总长达91.5m，均匀分布3个核心筒，由于设计中在核心筒下布置刚度较大变形调节装置，因此土应力分布较为均匀。

路径2～4沿筏板基础横向布置。其中路径2和4位于核心筒下，基底土压应力表现出刚性基础的“马鞍形”分布。基底土应力于“注浆”后开始逐渐稳定，最终趋于收敛。路径3位于两个核心筒之间，由于结构刚度及质量均较集中于平面的下部，在偏心荷载作用下，基底土反力呈现处向一侧倾斜。对比路径2～4，除了筏板端部土应力较小外，筏板内部土应力最大差值分别为44.5kPa、35.3kPa、43.5kPa，其中，路径2和4为上部核心筒区域，结构刚度较大，由于架越作用的影响，土应力差值较大。

图9 路径1(1#～18#)土应力

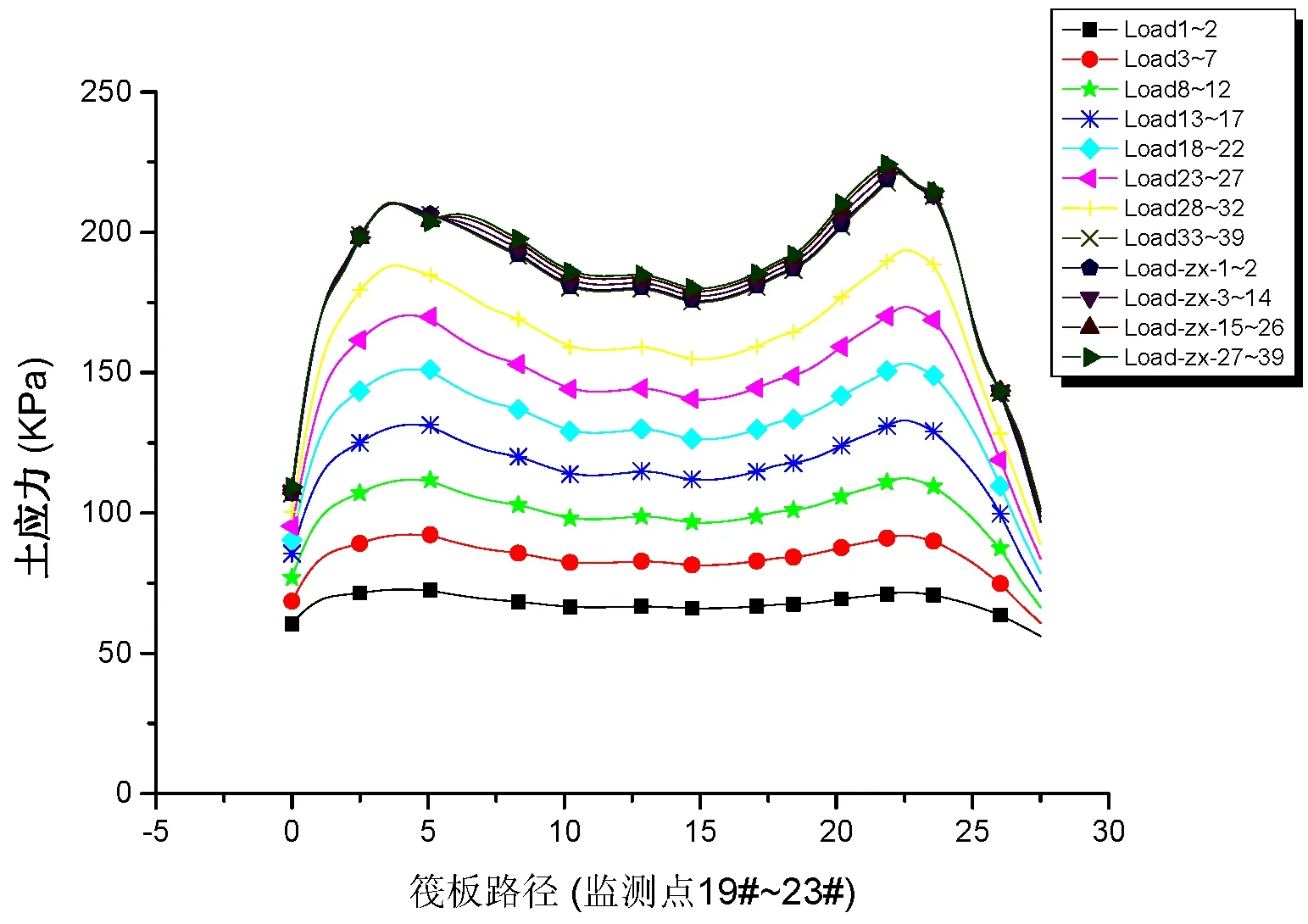
图10 路径2(19#～23#)土应力

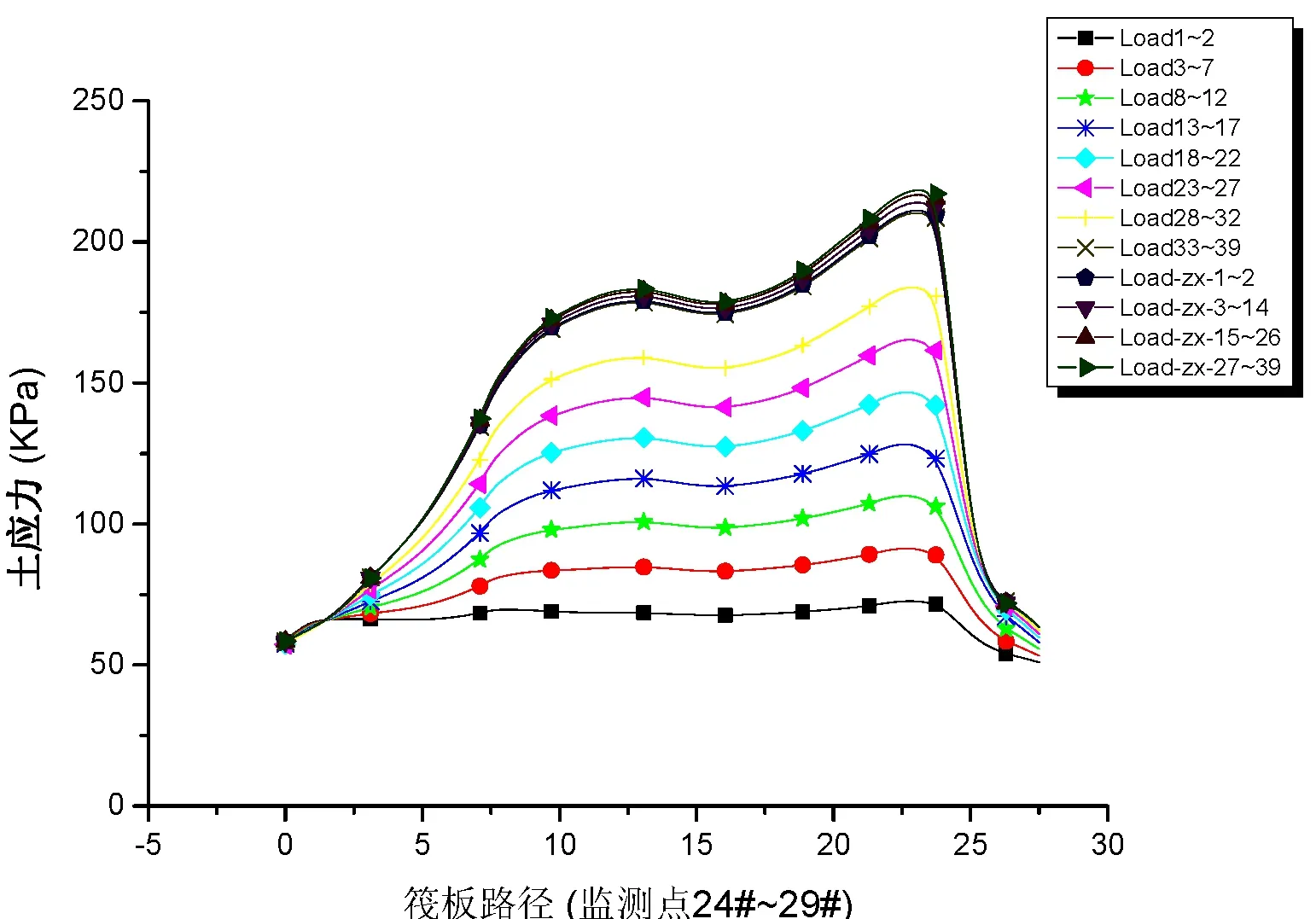
图11 路径3(24#～29#)土应力

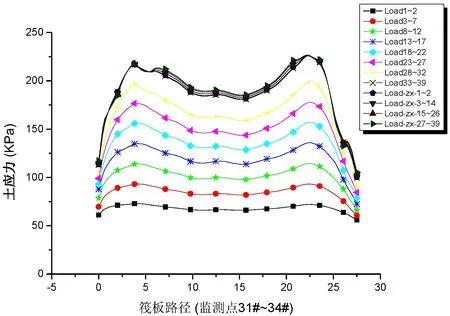
图12 路径4(31#～34#)土应力

3.2.3桩顶反力

为对比实测桩顶反力，沿路径1提取各桩顶反力，得到图12，其中路径1沿着建筑物纵向，2#、3#、5#、6#、8#、9#桩位于主楼核心筒区域，桩顶变形调节装置刚度为180 000kN/m，其余刚度为120 000kN/m。路径2、3均是沿着建筑物横向的核心筒区域。

从图13中可以看出，在加载初期，各桩顶反力分布均匀，这是由于此时荷载较小，筏板抗弯刚度较大，能够均匀传递上部荷载。随着加载进行，调节装置刚度大的核心筒区域荷载较大，桩顶反力增长较快，最大值为7056kN。模型桩顶反力与设计的单桩承载力基本吻合。

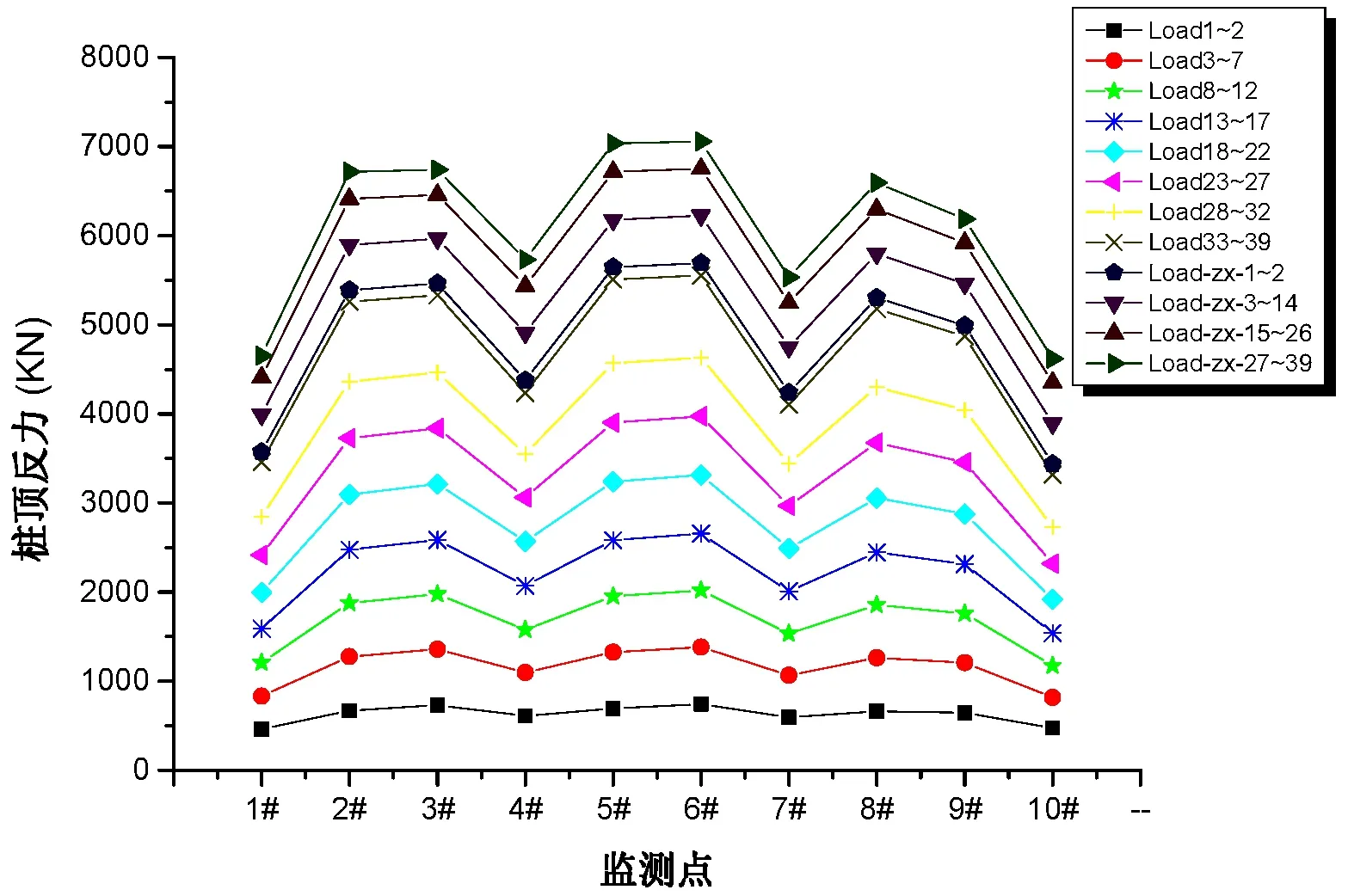
图13 路径1(1#～10#)桩顶反力

3.2.4桩土荷载分担比

图14为桩土荷载分担比。在加载开始到第一步结束，桩荷载分担比从0迅速增长至51.5%，地基土分担比锐减为48.5%。随后，桩土荷载分担比保持相对平稳，随着荷载的增加，桩所承担的荷载比例缓慢增长，土体荷载分担比缓慢减小，直到进入第二阶段，桩承担的荷载比例增速有所提高，最终桩分担比达到63.6%，土体减小至36.4%。图13可以看出桩土荷载分担比存在两阶段特性。

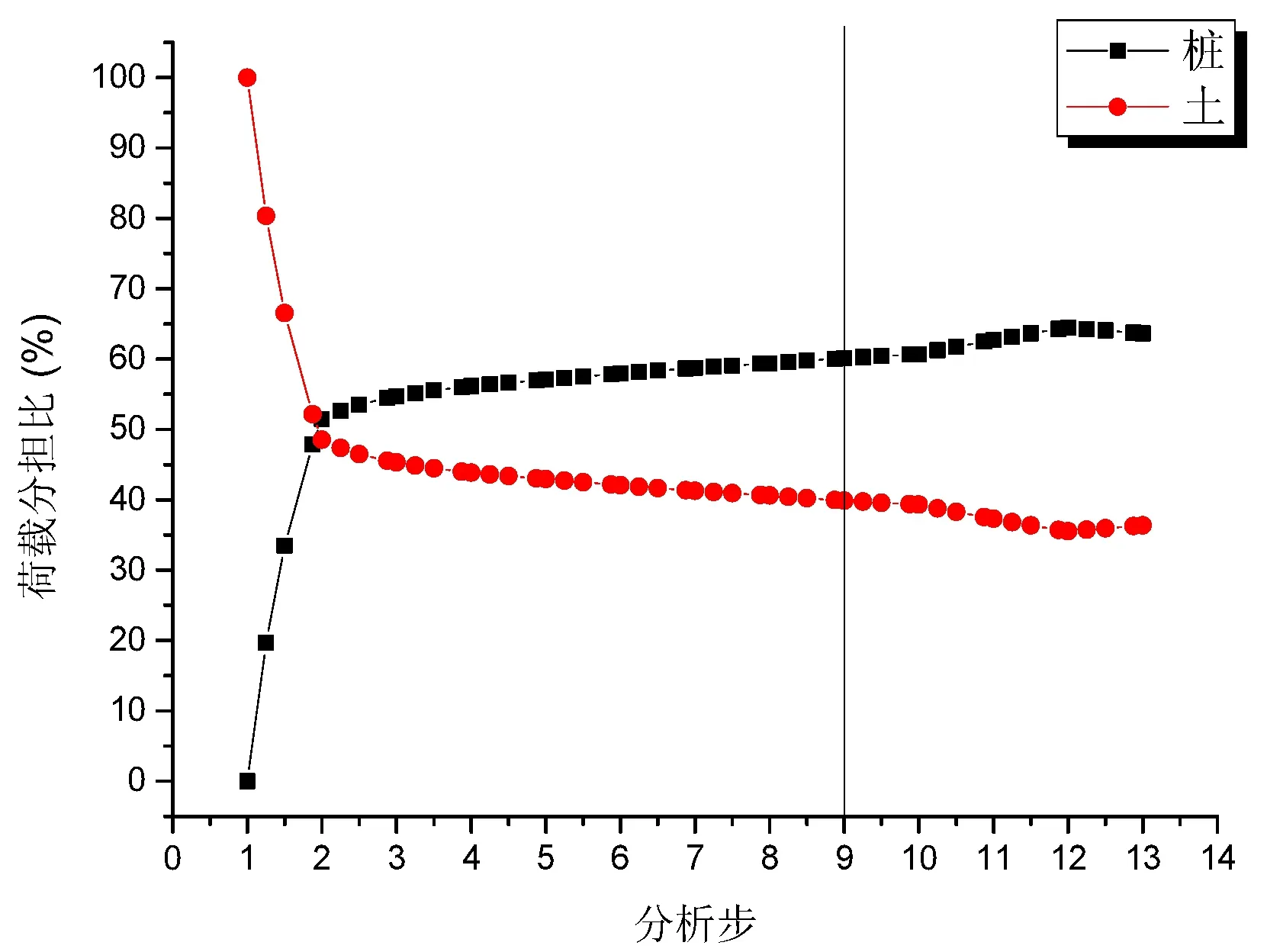
图14 桩土荷载分担比

3.2.5桩侧摩阻应力

两阶段变刚度复合桩基产生负摩阻力的原因与常规桩基不同，其作用机理是土体先被压缩分担上部荷载，相对桩有向下的位移，对桩身上部产生向下的负摩阻力，中性点位于约0.8倍桩长位置，随着荷载的增加不断沿桩身上移。在加载过程中，复合桩基大部分处于负摩阻力状态。

图15为桩侧摩阻应力沿桩身呈阶梯状变化，沿着桩身从上向下，桩侧的负摩阻力先缓慢增大至-26kPa，随后在0.4倍桩身长度附近减为零，即中性点的位置；再沿桩身往下，负摩阻应力又迅速增大为97.2kPa，在桩底处减小为0。

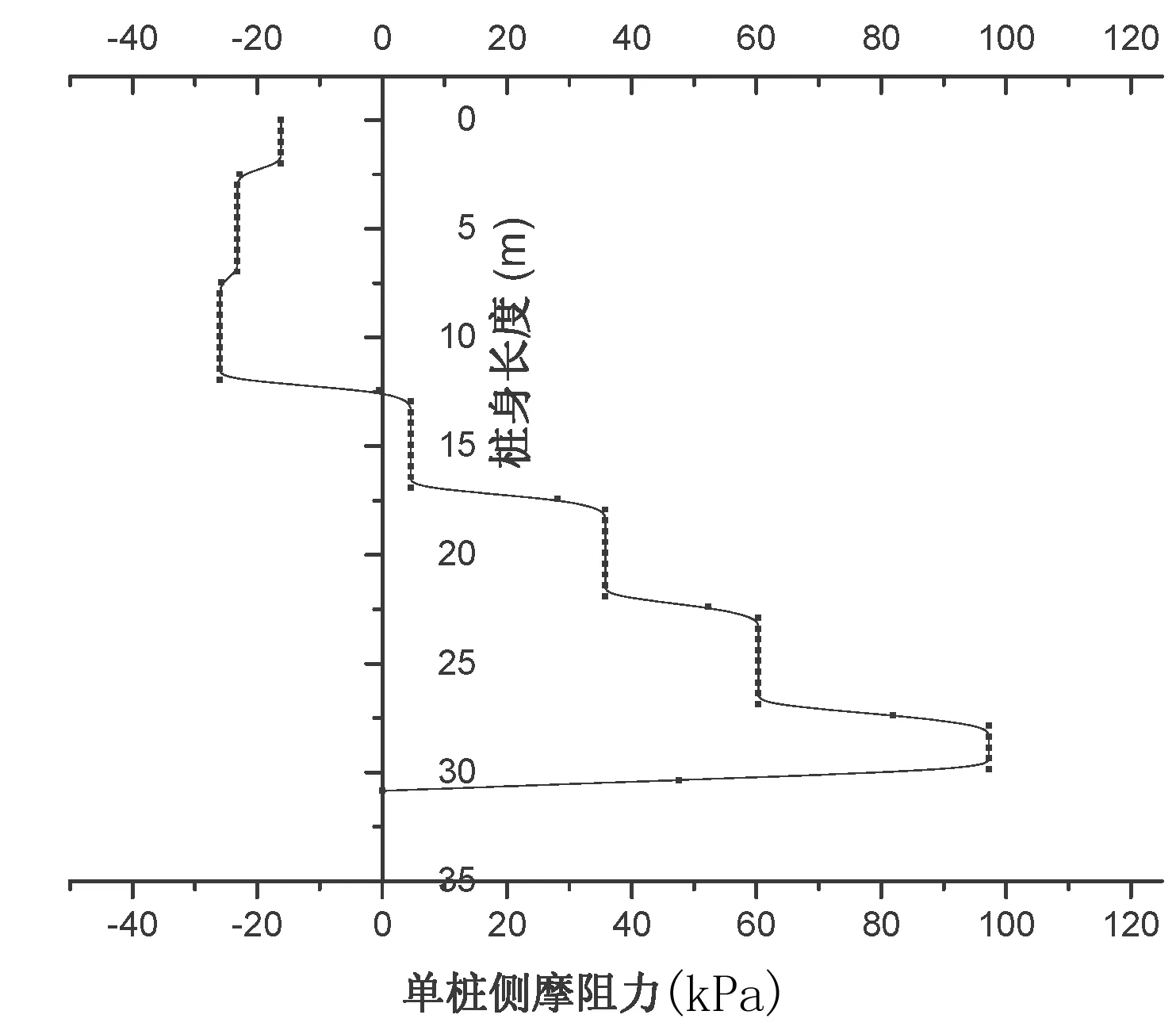
图15 桩侧摩阻力

复合桩基的两阶段变刚度特性决定了其将产生负摩阻力，在加载过程中，桩身0.4倍桩长以上部分均侧摩阻力均为负值，在设计时不能忽略此段负摩阻力对基桩的不利影响。

值得探讨的是，本节关于桩侧负摩阻力的研究是基于桩长为30m的情况，桩身0.4倍桩长以上部分范围受负摩阻应力的作用，其影响应引起重视。地基土的受荷变形，主要体现在表层一定深度内，对于不同地质条件下的不同桩长，尤其是桩长比较短的情况，其桩侧负摩阻应力的影响范围相对更大，因此不同桩长的桩侧摩阻力影响有待进一步研究。

4 结论

本文以实际应用工程七星公馆2#楼为例，对两阶段变刚度复合桩基础进行设计，通过数值模拟结果分析，验证两阶段变刚度设计的合理性。

(1)七星公馆2#楼复合桩基础变形呈“碟形”，其特性与常规筏板基础相似。基础的沉降呈现两阶段特征，第一阶段沉降量较大，第二阶段沉降量相对较小。

(2)两阶段变刚度复合桩基础基底反力分布，沿建筑物纵向土应力分布较为均匀，沿横向呈现“马鞍形”分布。

(3)桩顶反力第一阶段开始逐步发挥作用，第二阶段平缓增长，上部荷载主要由桩基承担。

(4)复合桩基础桩土荷载分担比也具有两阶段特性：第一阶段桩荷载分担比缓慢增长；到第二阶段，桩分担比增速有所提高。

(5)复合桩基两阶段变刚度特性决定了其产生负摩阻力，在加载过程中，桩身上半部分处于负摩阻力状态，中性点位于距桩顶约0.4倍桩长，因此计算时不能忽略负摩阻力对基桩的影响。

[1] 宰金珉，周峰，梅国雄，等.端承桩复合桩基及其设计方法[J].工业建筑，2008，38(1)：60-64.

[2] JGJ94-2008 建筑桩基技术规范[S].北京：中国建筑工业出版社，2008.

[3] 林树枝，郭天祥，汪亚建，等.基于ABAQUS程序的两阶段变刚度端承桩复合桩基有限元分析[J].福建建设科技，2013(4)：5-8.

[4] 石亦平，周玉蓉.ABAQUS有限元分析实例详解[M]．北京：机械工业出版社，2007．

[5] 费康，张建伟.ABAQUS在岩土工程中的应用[M].北京：中国水利水电出版社,2010.

[6] 郭天祥.基于数值分析的两阶段变刚度复合桩基础工作机理研究[J].福建建筑，2015(8)：59-64.

[7] 陈勇华.土体压缩模量、变形模量和弹性模量的讨论[J].科学技术，2010(66):135-136.