基于BP神经网络模型在珊溪水库水华预测中的应用

王 珅，万哲慧，冯孙林，黄 晶，刘秀峰，赵小敏

(1.浙江省温州市环境监测中心站，浙江 温州 325000；2.山东省枣庄市环境监测中心站，山东 枣庄 277100)

1 前 言

“十二五”以来，温州市各级人民政府及其环境保护部门日益重视饮用水地的环境保护。温州市民饮用水主要来源的珊溪水库作为国家重点控制的地表水饮用水源地二级保护区，确保饮用水安全尤为重要。然而珊溪水库富营养化导致的水华现象时有发生，常规监测项目的水环境质量评价不具有预见性，导致水库水质变化趋势未能进行科学研判。因此，新形势下，对环保主管部门“眼睛”环境监测的工作提出了更高要求，不仅能分析现状，还应该具有趋势预测与研判的能力[1-2]。

BP(Back-Propagation Network)神经网络作为人工神经网络ANN(Artifical Neural Network)范畴的黑箱模型通过输入层、隐含层、输出层的非线性函数多次拟合与高维映射展示了较强的自我学习与适应能力。近年来，国内外基于BP神经网络建立的水环境数学模型在水环境质量评价与水质预测中的应用报道较多[3-4]。

2 水质检测与数据采集

2.1 水样采集

珊溪水库位于(东经119°50′～120°20′，北纬47°39′～47°48′)，22个采样点位如图1所示。温州市环境保护局珊溪水利枢纽分局依据《水质 湖泊和水库采样技术指导 (GBT 14581-1993) 》《水质 采样方案设计技术术规定 (HJ 495-2009) 》承担珊溪水库库区和交接断面水质公开方案的布点与采样作业。

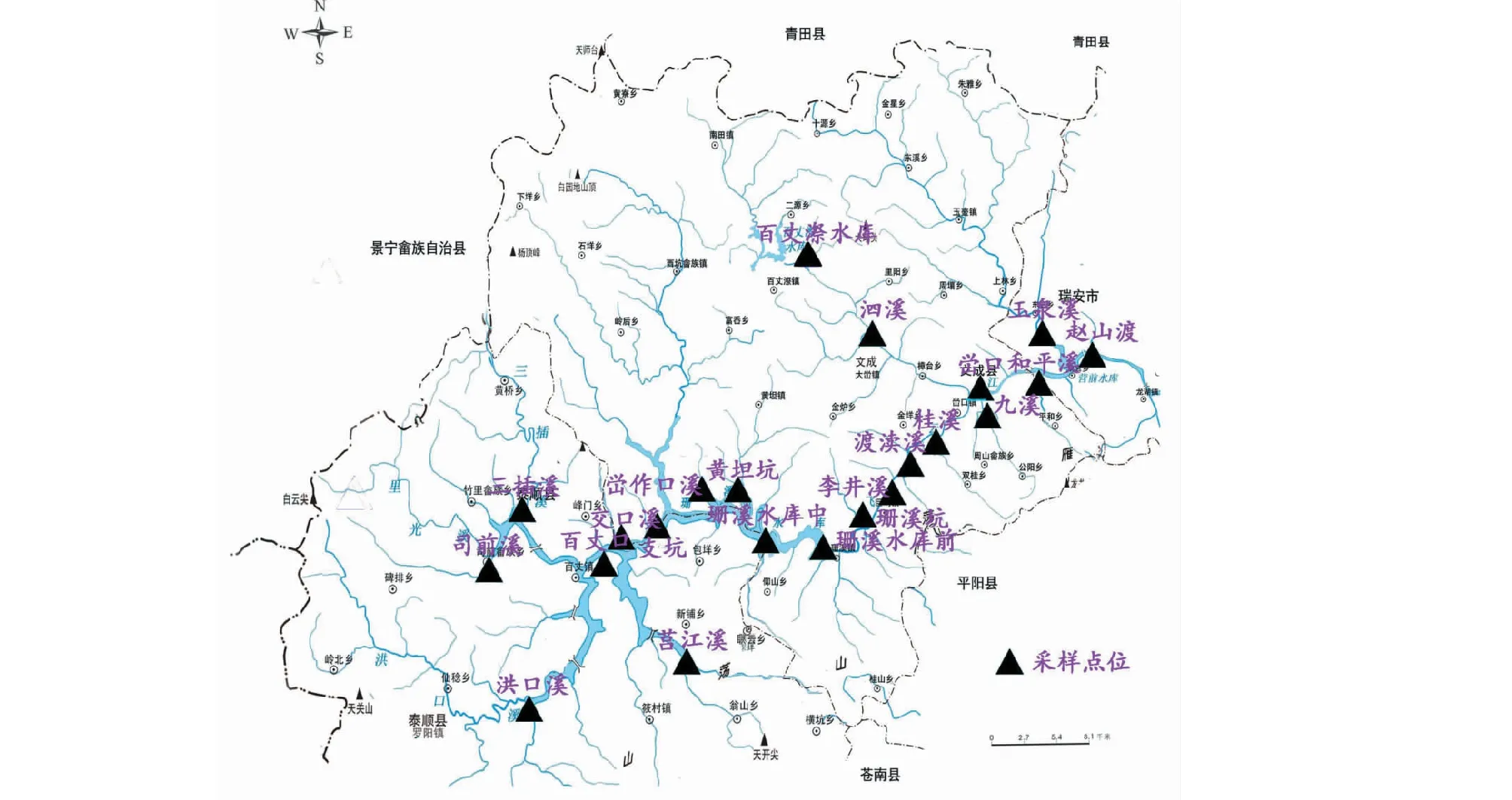
图1 珊溪水库水质采样布点示意图Fig.1 Distribution of sampling sites of Shanxi reservoir

2.2 实验方法与设备

表1 实验分析方法与设备Tab.1 analysis method and equipment

3 Matlab的BP神经网络预测模型设计

3.1 BP神经网络算法

BP神经网络算法利用数据样本进行不断重复地调整学习，直到满足设定的误差范围内，以此建立数据模型。其训练过程分为正向传播与反向传播两个阶段：样本的数据矩阵经输入层、隐含层运算处理至输出层；未能获得期望值的数据矩阵又逐层逆运算并调整实际输出值与期望输出值的差值，以此调节权值。正向、反向传播相结合最终获得期望的输出值[5]。

(1)

(2)

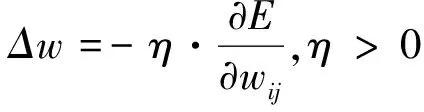
(3)

式(1)为反向传播过程中，将目标函数Ek确定为误差的平方和。n为输出层节点个数，dik表示第k个样本的第i个期望输出值，yik表示第k个样本的第i个实际输出值。样本总数为S的总误差E由式(2)定义。式(3)步长定义为η；迭代次数为t。

运用Levenberg-Marquardt优化算法[6](LM算法)，该算法采用近似二阶导数信息，适用于中小规模网络，收敛速度与收敛精度较其他算法强。

输入层、输出层设定为相关水质参数。式(1)中输出层第i个神经元在t时刻的实际测定浓度值为dik(t)，期望输出值为yik(t)，n为输出层神经元个数。t时刻BP网络误差函数Ek(t) 小于预先给定的误差值时，网络训练停止进行并获得神经网络预测模型。

3.2 MATLAB R2015b可视化建模

MATLAB应用包中提供的神经网络设计及仿真GUI为BP神经网络建模与数据分析工作带来了极大便利。用户通过友好的人机可视化交互界面可以简便地操作MATLAB各项功能，实现数据建模与模拟仿真。在主界面命令窗口输入nntool打开神经网络数据管理对话框。在“Input Data”导入pH值、高锰酸盐指数、总氮、总磷数据矩阵；“Target Data”导入对应叶绿素a数据。点击“new…”创建珊溪水库水华预测模型，设置参数见图2。其中隐含层神经元数目选择20个，选择tansig为传递函数。训练结果见图3。

图2 MATLAB GUI BP神经网络模型创建及模型参数设置Fig.2 MATLAB GUI BP neural network model establishment and model parameters setting

图3 BP神经网络模型样本训练Fig.3 Sample training of BP neural network

4 结果讨论与建议

4.1 讨论

珊溪水库流域水质发生物理、化学、生物共同作用，多因素决定珊溪水库水质状况变化。珊溪水库复杂水体处于动态平衡状态，外来污染因子产生的污染相对稳定；因此可以采用预测方法实现相关水质指标预测。

水质数据的完整性与连贯性对预测模型精度至关重要，水质数据包含的变化规律越多，预测模型越准确[7]。2010年珊溪水库应急监测获得115组实验数据。MATLAB将115组数据作为输入样本集分为训练集、验证集、测试集。BP仿真神经网络进行训练、验证、测试、汇总，结果如图4所示，训练集输出数据与目标数据相关性R值0.993，表明网络训练集模型输出数据与目标数据相关性较好，验证集、测试集相关系数分别0.891、0.966，表明BP仿真神经模型稳定性较好。在图4中，叶绿素a预测值与实测值两组数据相关系数为0.978。从图5、图6预测值误差曲线曲线分析，可以看出：误差平均值-0.19%，标准方差18.54%，模型精度基本符合要求。

图4 BP神经网络训练结果回归分析Fig.4 Regression analysis of BP neural network training results

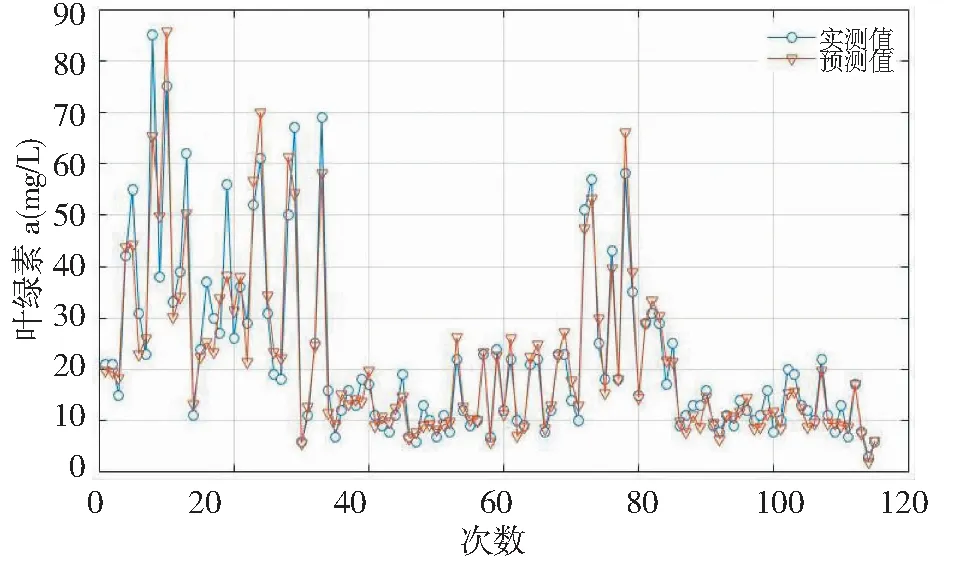
图5 叶绿素a预测值与实测值比较Fig.5 Comparsion of predictive values and measured values of Chl.a

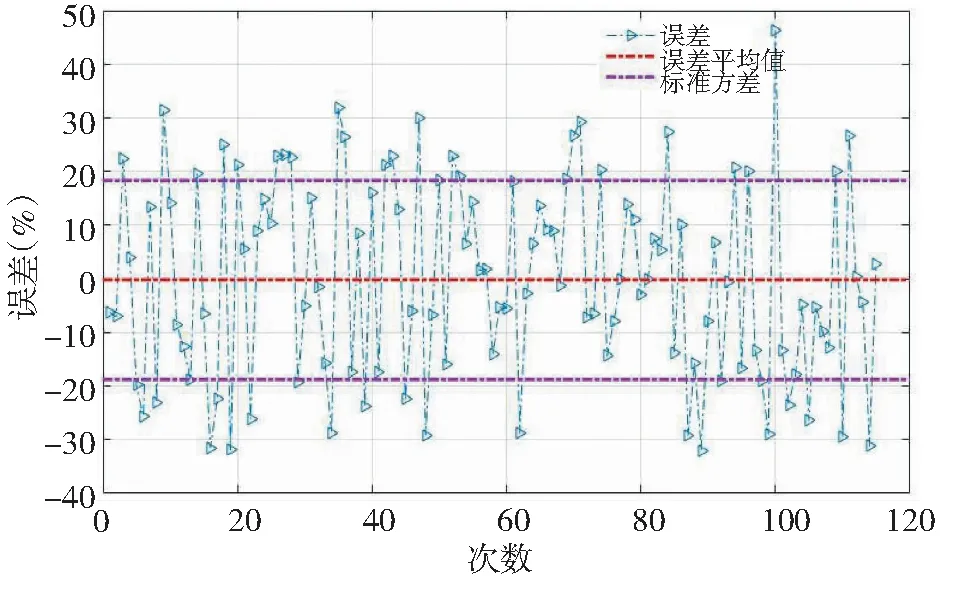
图6 叶绿素a预测误差Fig.6 Prediction error of Chl.a

4.2 建议

4.2.1 本次获取的水质数据矩阵数量有限，应继续增加样本空间，提高预测模型的准确度。珊溪水库水质变化是珊溪水库水域系统整体变化的体现，受系统内外因素的协同作用，若受外因作用越大，基于珊溪水库水质监测数据的预测效果会减弱。因此，大数据建模时应考虑外部因子输入。

4.2.2 在水质建模的基础上嵌入GIS模块，应用GIS对水质预测数据的处理与分析，实现计算结果的可视化，结合专家经验可对各时间段珊溪水库水质进行科学预测。

5 结 论

利用MATLAB R2015b建立了珊溪水库水华BP神经网络预测模型，模型输出数据与实测叶绿素a数据相关性R值0.978相关性较好，模型稳定性较好。叶绿素a预测结果与实际测定基本相符，平均误差较小。同时，对模型精度的提高与BP神经网络与GIS结合发展方向提出了建议。

[1] 王 涛,刘足根,史晓燕.Matlab在建设项目地表水环境影响预测评价中的应用研究[J].环境科学与管理,2016,41(3):163-165.

[2] 杨 岳,关成立,陈兴汉.基于Matlab的BP神经网络模型在漠阳江水质评价中的应用研究[J].环境科学与管理,2014,39(11):161-165.

[3] 张 文,王 莉.基于T-S 模糊神经网络的颍河水质时空变化特征分析[J].环境科学与技术,2015,38(12):254-261.

[4] Wu Wenyan,Dandy G C,Maier H R.Protocol for developing ANN models and its applicationto the assessment of the quality of ANN model development process in drinking water quality modeling[J].Environmental Modelling and Software.2014.54:108-127.

[5] 孙莉宁,张之源,罗定贵.基于Matlab实现的ANN方法在巢湖水质评价中的应用[J].安徽大学学报(自然科学版),2005,29(2):90-94.

[6] 徐华山,徐宗学,唐芳芳,等.漳卫南运河流域水质时空变化特征及其污染源识别[J].环境科学,2012,38(2):359-369.

[7] Zhang Q,Li Z W,Zeng G M,et al.Assessment of surface water quality using multivariate statistical techniquesin Red Soil Hilly Region:a case study of Xiangjiang watershed China[J].Environmental Monitoring and Assessment,2009,152(1/2/3/4):123-131.