表面效应对动态光散射纳米粒径测量的影响

叶智彬，许继森，邱 健，彭 力，骆开庆，韩 鹏

（华南师范大学物理与电信工程学院；广东省光电检测仪器工程技术研究中心，广东广州510006）

动态光散射（dynamic light scattering，简称DLS），也称准弹性光散射或光子相关光谱技术[1]。该技术是基于溶液中纳米颗粒的布朗运动引起的散射光强随机涨落，通过对散射光强信号相关分析和反演，获得颗粒在溶液中的颗粒粒径大小及分布。

在通常的测量中，一般采用10 mm×10 mm×15 mm的四面通光比色皿盛载样品，对于某些造价昂贵、难以大量获得的样品，通常会考虑使用1 mm×10 mm×15 mm乃至更小宽度的四面通光的微升级比色皿进行盛载，而此时样品池可看作两端近壁面的微流通道。然而，已有文献指出[2-3]，在这种两端近壁面的微流通道内，壁面的表面作用对颗粒布朗运动的影响不可忽略，表现为微流通道内颗粒溶液的实际黏滞系数与自由空间下溶液黏滞系数有着较大的差异，且这种差异会随着通道宽度的减小而进一步扩大。根据动态光散射理论，黏滞系数的改变势必会对测量结果产生影响，却未见有相关研究。其实，对已有相关文献的类似实验结果进行统计，发现在宽度受限的微升级样品池环境下，其所测得的颗粒粒径与正常的测量值有较大的偏差，但文献一般均将产生该偏差的原因归结实验结果的偶然误差[4]。

为了验证通道宽度对DLS测量结果的影响并探究其规律，本文中设计了一维宽度可调的样品池结构，通过机械装置控制微通道宽度范围为0.6～2 mm，模拟微量样品池的测量环境；并以高速线阵CCD为探测器，取代传统光电倍增管（PMT）探测，结合线阵CCD多点并行探测的优势，搭建动态光散射实验测量系统，同时测量微通道与外部自由空间的颗粒溶液。以不同粒径的二氧化硅标准颗粒溶液作为样品，对微通道内外测量结果进行分析和对比，提出了针对黏滞系数变化的粒度测量结果补偿方案。该研究对于采用微量样品池的动态光散射测量有重要意义。

1 实验

1.1 动态光散射法原理

当激光光束照射溶液介质时，由于溶液介质的非均匀性或者其它介质的存在，使除了入射光方向以外其他方向也能观察到光强的现象称为光散射。根据动态光散射理论，当一束激光入射到纳米颗粒悬浮溶液中时，散射光的涨落快慢反映了颗粒的布朗运动速度的大小[5]。实际中通过对散射光的自相关曲线进行反演运算得到颗粒布朗运动的扩散系数，从而得到颗粒的粒径大小及分布信息。假设光路中探测器接收到的散射光强为I（t），那么颗粒的散射光强自相关函数G（2）（τ）[8]为

式中：I（t）和I（t+τ）分别是t及t+τ时刻测得的颗粒散射光信号；τ是延迟时间。

对于单分散颗粒而言，自相关函数为一个指数衰减函数，可表示为

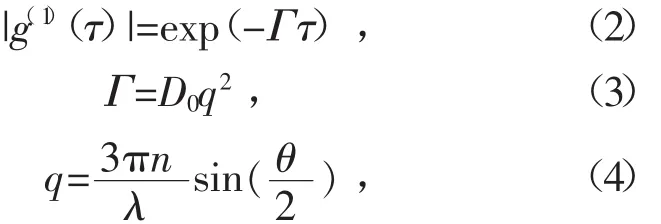
式中：Γ为衰减线宽，表示散射光光强自相关曲线衰减快慢；q为散射矢量；λ为入射光源的中心波长；n为溶液折射率；θ为入射光与散射光之间的夹角；D0为理想稀溶液中球形颗粒布朗运动的自由扩散系数，而由Einstein-Stokes关系式可知

式中：kB为玻尔兹曼常数；T为绝对温度；η0为溶液的粘滞系数；d为粒子的直径。从式（5）可知，在单分散颗粒系的条件下，通过测量散射光场的自相关函数便可以求得粒子的扩散特性、大小及其分布等信息。

1.2 固-液界面壁对测量结果的影响

在溶液中作布朗运动的颗粒在固液界面壁会受到表面效应的影响[3]，表面效应指粒子在固液界面附近的扩散受到固体壁面的影响，从而导致了扩散速度减小的现象。当粒子的半径为R，悬浮在黏滞系数为η0的介质中，以v的速度自由移动，则斯托克斯公式可以表示为

由式（6）结合Einstein流场方程即可得到式（5），然而，当液体受到容器壁限制时，在器壁与溶液的分界面处颗粒受到黏滞阻力增大，导致在固液界面附近的黏滞系数η0增大，此时需要考虑对黏滞系数作出修正，则斯托克斯公式表示为：

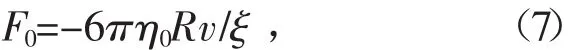
式中ξ表示与界面性质相关的修正因子值。将修正因子ξ代入（5）式后可得

修正因子ξ与壁面宽度有关，在无穷大的自由空间内，ξ值为1，随着壁面间距离的减小，ξ也不断减小，ξ为小于1的值[2]。由式（8）可知，ξ的引入会导致管壁间溶液实际的黏滞系数变大，从而使管壁附近的扩散系数变小，并且随着壁面宽度不断收窄，颗粒与管壁间的距离会不断减少，从而管壁与溶液分界面处颗粒受到的黏滞阻力不断增大，此时对应的修正因子值ξ也会不断减小。但在一般的动态光散射法测量中，在温度一定的条件下，黏滞系数视作一定值，此时修正因子值ξ恒等于1。当颗粒溶液处于宽度较小的微通道当中时，溶液非常靠近两侧的管壁，此时测量所得的偏小的扩散系数将直接导致计算所得的粒径测量值变大。

另外，在文献[6]中也发现，对于管径较小的毛细管，由于管内壁面表面效应的影响，表现为其黏滞系数的测量值均大于理论值，且黏滞系数测量值会伴随着毛细管内径的减小而增大。该实验结果验证了样品池壁面间的宽度确实会对颗粒的有效黏滞系数产生影响，进而影响颗粒的布朗运动。

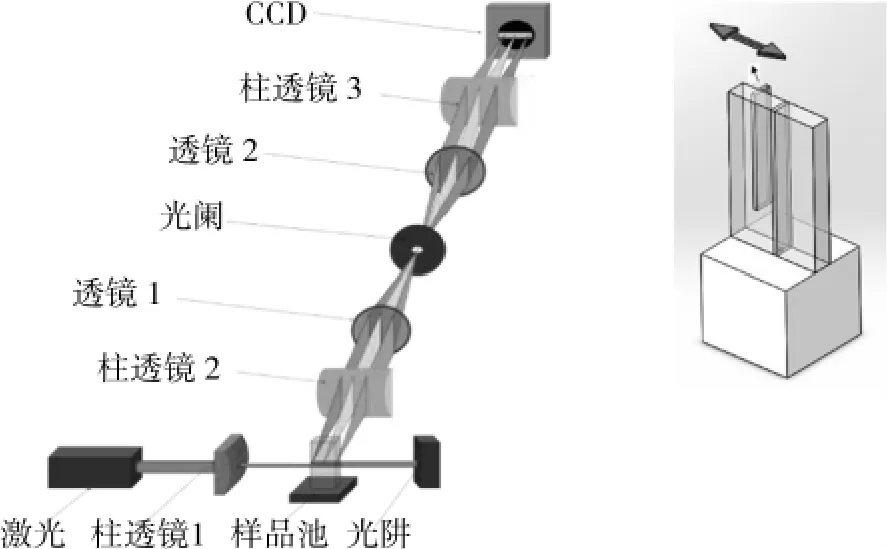
图1 系统原理图Fig.1 System schematic diagram

1.3 装置

为了探究微通道中布朗运动的状态，需要同时对通道内与通道外自由空间布朗运动进行测量，然而传统的以光电倍增管为探测器的单点探测系统无法实现上述功能。为此，本文中采用以高速线阵CCD为探测器的图像法动态光散射系统[16]，其系统结构图如图1所示，主要包括入射系统、样品装置系统、成像系统3大部分组成。

如图所示，激光器发出的激光经过柱透镜会聚后入射到装有纳米颗粒的样品池中，颗粒受到激光照射产生散射光，由于颗粒的布朗运动，散射光信号会呈现出起伏涨落，此时我们通过CCD在90°的方向上对散射光强信号进行高速连续捕捉，并以图像形式保存。

在散射光接收光路的设计上，为了避免不同角度散射光对于测量结果的影响，本系统在成像系统光路上采用了4F透镜接收系统，如图1所示。通过该接收系统，保证了CCD上每个像素点位置所接收的散射光均来自于样品池上对应位置的90°散射光，排除了非信号光的干扰，实现对不同位置间的粒径分布进行测量，从而实现对窄通道内外的测量结果进行对比。

在样品池系统设计部分，为了能同时测量窄通道内外样品溶液且实现宽度可调，我们设计了如图1所示的样品池结构及微移装置，样品池为中间分隔石英四通光样品池，尺寸为5 mm×10 mm×15 mm，为了减少接收光路上透镜像差所带来的测量结果干扰，我们选择在样品池中间位置固定一块厚度为1 mm的光学玻璃作为固定端。而在其中间附近区域设置另外一块厚度为1 mm的光学玻璃板作为活动端，该活动玻璃板连接有微移装置，微移装置可调范围为0～2 mm，最小精度达10 μm。在实验中，通过调节微移装置，便可以实现活动端玻璃板移动距离的准确操控，实现对微流通道宽度的准确调节。

1.4 数据处理

图2为CCD 1 s（帧频f=10 kHz）拍摄记录下的400 nm标准颗粒散射光强图像，图中在水平方向上分布着1 024个像素点，竖直方向上为每隔0.1 μs拍摄后共1 s内拍摄的10 000张照片，构成一幅散射光强合成图，从图上可以很明显地看出颗粒的散射光强，受颗粒布朗运动的作用光强呈现随机的变化，这些随机变化的光强即是光散射信号。线阵CCD拍摄的每幅合成图上的1 024个像素点（1 024×n）均记录了某时刻此像素点的散射光信号，则每1次测得的动态光散射信号图像n帧，每帧图像的采样时间间隔为τ=1/n，对每个像素点上的照片进行公式（1）—（5）的数据处理，便可以得到相应位置的纳米颗粒粒度。

图2线阵CCD散射光强图Fig.2 Linear CCD scattering intensity

图3所示粒径为356 nm颗粒在0.6 mm受限宽度内的扩散系数分布，需要说明的是，图上的过渡部分（约300～400及580～680像素点位置）光强平均值低于整体光强平均值80%以上，可知该部分样品池界面处的玻璃壁。由于该部分区域为固态壁面，此处散射光强非常弱，无法计算扩散系数，因此在此处扩散系数设定为0。

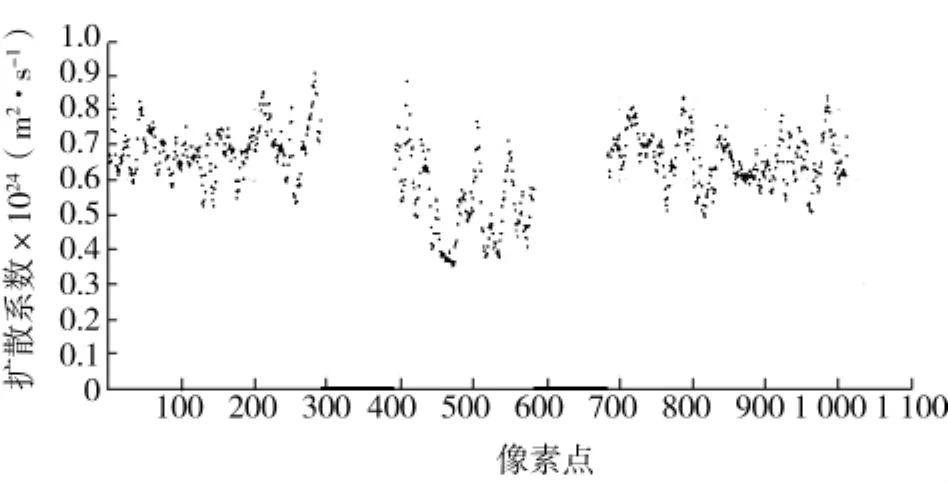
图3 356 nm颗粒在0.6 mm空间宽度的扩散系数分布Fig.3 Diffusion coefficient distribution of 356 nm particle in 0.6 mm width space

2 结果与讨论

2.1 系统可靠性验证

为了验证CCD系统测得的实验数据的可靠性，选择3种不同粒径的标准SiO2颗粒的溶液在正常的测量条件下进行实验测量，并与传统动态光散射仪器（BT-90动态光散射粒度分析仪，辽宁丹东百特仪器有限公司生产）实验结果进行对比。每组样品测量10次，测量结果取平均值，如表格1所示。

由表可知，对比CCD系统与BT-90的测量结果，测量结果相对误差均在4%以内，证明CCD系统能获得正确的测量结果。

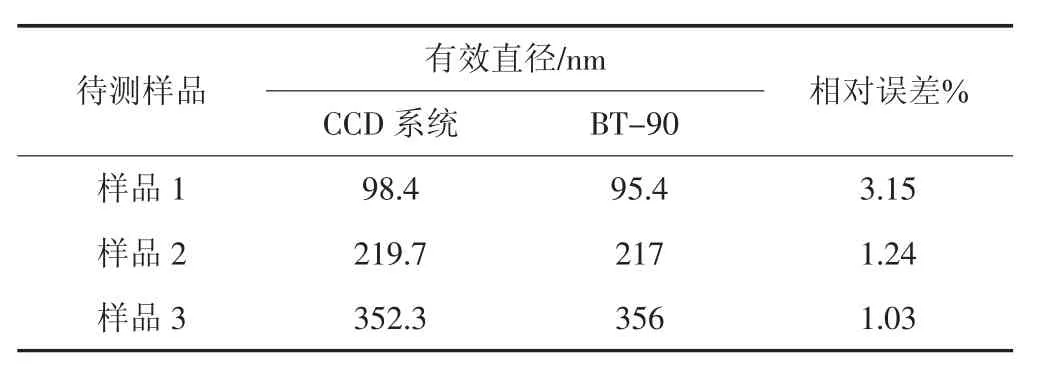
表1 CCD系统与标准BT-90粒度测试仪的实验结果对比Tab.1 Experimental results of contrast between CCD system and BT-90 instrument

2.2 颗粒在近壁面环境下的扩散系数分布

为了验证在宽度受限的微通道内扩散系数的分布情况，调节通道宽度为0.6 mm，对3种粒径不同的标准纳米颗粒样品进行测量，并对整个样品池进行扫描计算，各粒径扫描结果如图4所示。

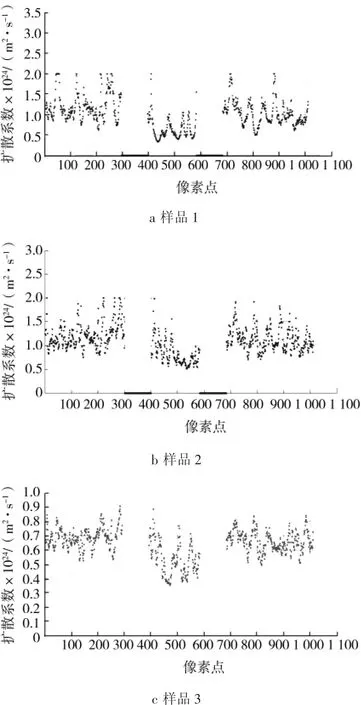
图4 不同粒径样品在0.6 mm空间宽度的扩散系数分布Fig.4 Diffusion coefficient distribution of different size particle in 0.6 mm width space

图4a、b、c分别为样品1、2、3在0.6 mm受限宽度内扩散系数的测量结果示意图。图像两侧对应为自由空间下（对应为0～300及700～1 000像素点）溶液的扩散系数分布，在通道外的空间下，溶液的平均扩散系数接近标准值；而在分布图中间部分（400～570像素点）则对应为微流通道区域的扩散系数分布，对微通道区域内外所测得的扩散系数进行统计平均，统计结果如表2所示。由表可知，对于不同粒径大小的颗粒溶液，在微通道区域内，其平均扩散系数都较两侧自由空间溶液的平均扩散系数小，从而验证了在微通道内溶液的黏滞系数会受到通道宽度的影响。

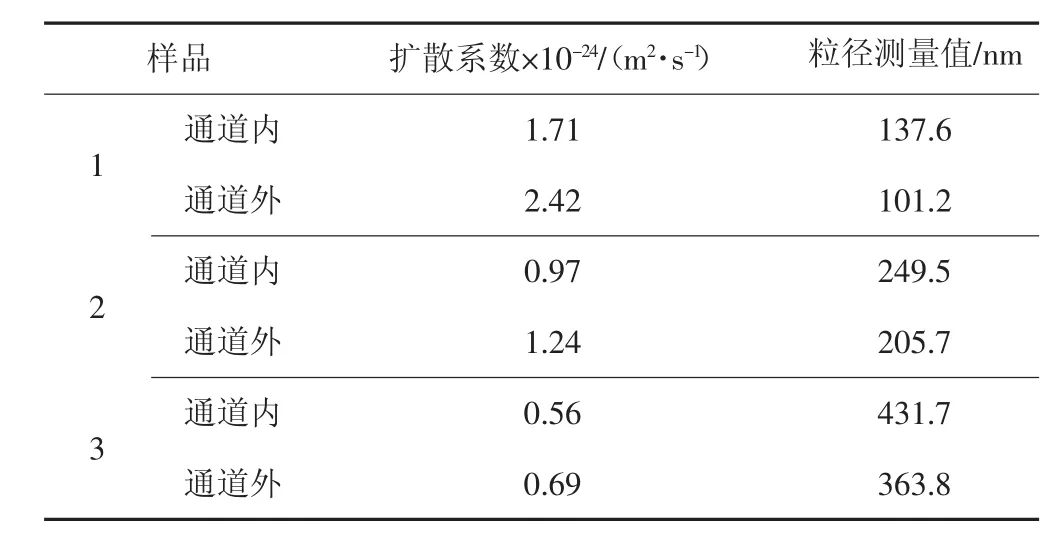
表2 不同样品颗粒在0.6 mm空间宽度的测量结果统计Tab.2 Measurement results of different particle in 0.6 mm width space

2.3 颗粒在空间宽度下的扩散系数变化

为了探究测量环境宽度与扩散系数间变化的规律，调节壁间宽度从0.6 mm开始调节，每增加50 μm为1组，测量3种样品在壁间区域内的平均扩散系数，测量10次取平均值，壁间宽度与3种粒径标准样品测得的扩散系数的变化趋势如图5所示

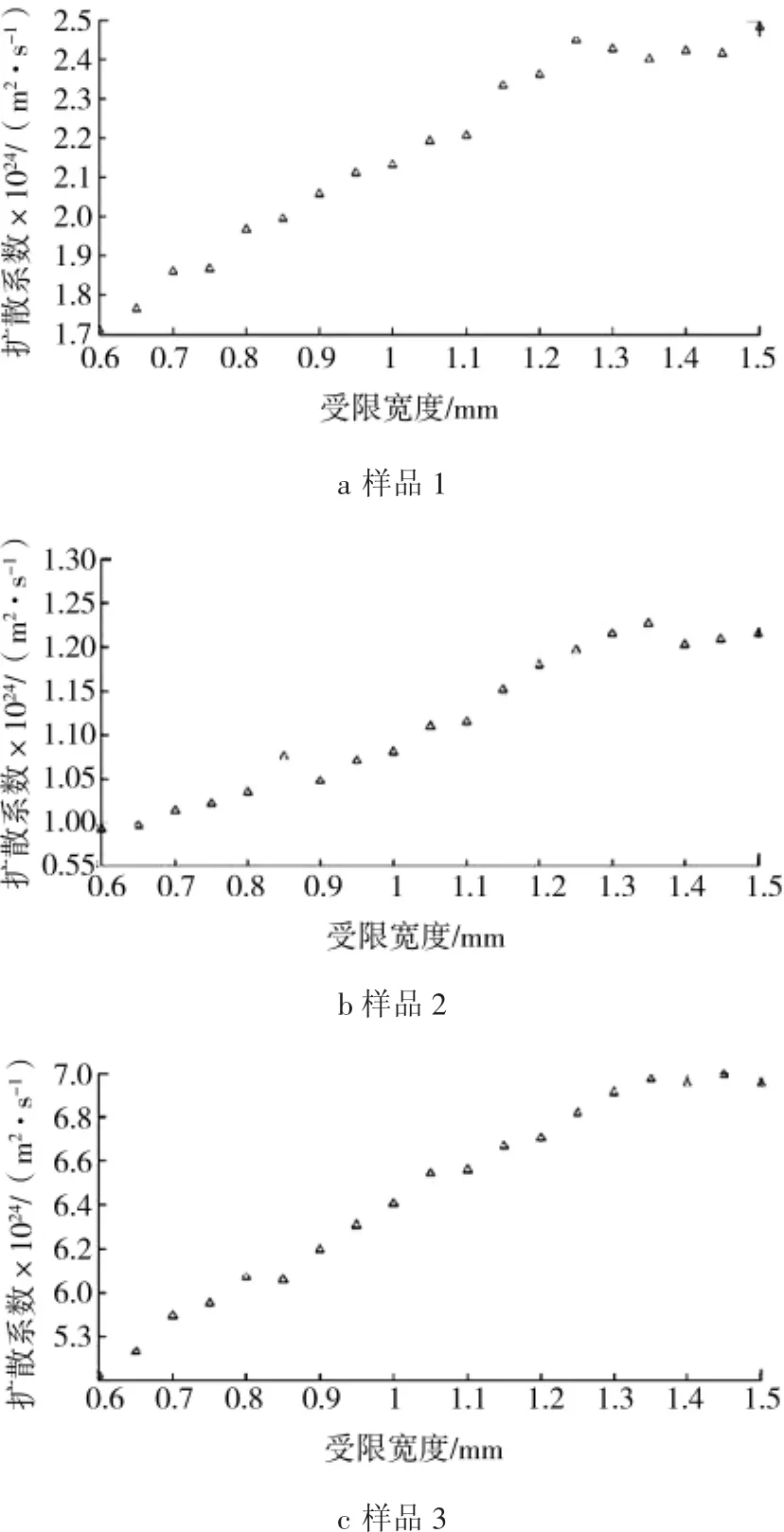
图5 不同粒径样品随空间宽度变化的平均扩散系数变化Fig.5 Average diffusion coefficient change with width of sam ples with different particle size

由图5a、b、c可知，当壁间宽度小于1 mm时，平均扩散系数均小于正常值，偏差均在5%以上，且宽度与扩散系数成近似线性关系。而当壁间宽度增大到1 mm附近后，扩散系数在某一值附近波动，其结果逐渐趋近于自由状态下的正常值。

2.4 对实验结果的修正讨论

根据上述的理论分析与实验结果，纳米颗粒在窄通道溶液内作布朗运动时，其扩散系数会小于自由空间中的自由扩散系数，进而导致窄通道内的粒径测量值大于实际值，因此，采用微量样品池的动态光散射测量，需要通过改变黏滞系数对测量结果进行修正。

已有文献提出了多种窄通道内液体黏滞系数的修正方案[2]，本文中推荐采用Pfahler等[7]提出的方法：对于窄通道内的微流体溶液，可以在Stokes公式中引入当量黏度η代替η0进行修正，使实际测量结果与理论结果一致。其具体修正方法如下：首先获取若干关键点（不同通道宽度）的实验扩散系数D1、D2、D3、……，依据Einstein-Stokes关系式求出对应环境下溶液的黏滞系数 η1、η2、η3、……，然后拟合出当量黏度系数的插值曲线及其函数关系，应用该曲线及关系就可以确定其他宽度下窄通道内液体的当量黏度系数，并根据修正后结果对扩散系数进行重新运算。

应用当量黏度对不同样品黏滞系数的测量结果进行修正，见图6—7。

应用该方法对不同粒径样品的实验结果进行修正，由图可以看到，修正后粒径结果与标准测量值误差均不超过3%，证明该修正方法可行有效。

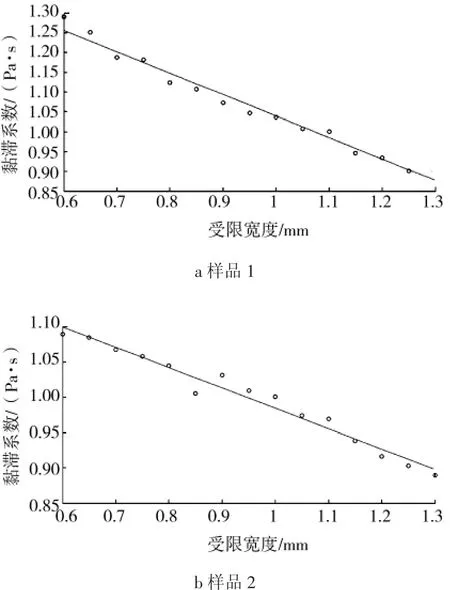
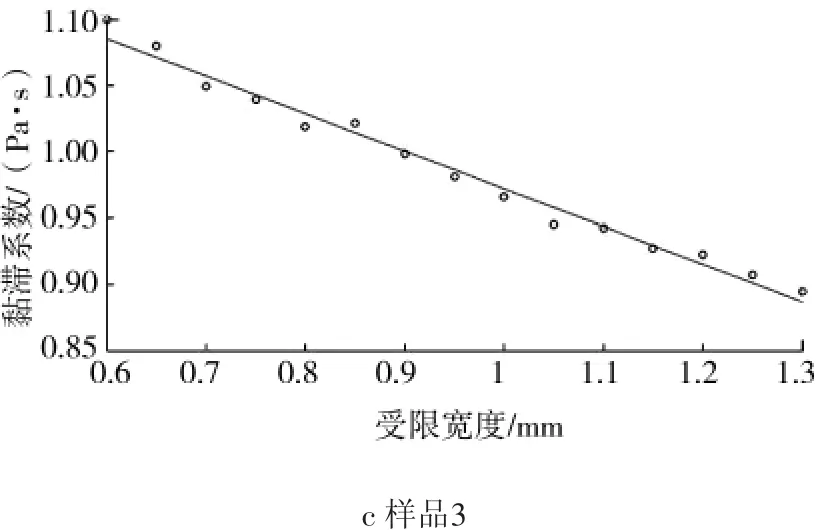
图6 样品颗粒当量黏度拟合直线Fig.6 Viscosity fitting line and correct results sample 1

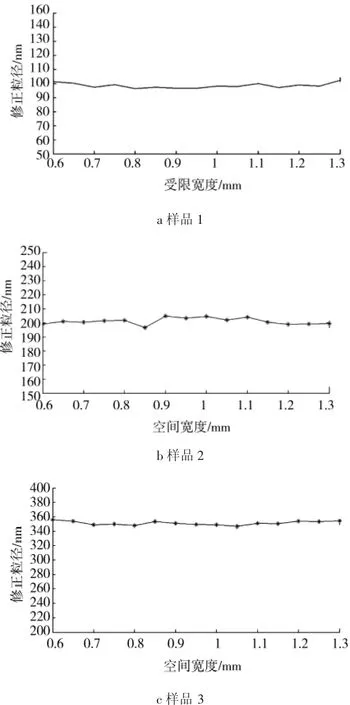
图7 样品颗粒粒径修正结果Fig.7 Size correction results of sample particle

3 结论

本文中详细研究了微量样品池对动态光散射法测量纳米颗粒粒径的影响。通过设计宽度可调的样品池结构，采用基于高速线阵CCD的动态光散射测量系统，系统研究了样品池宽度从0.6～1.5 mm变化时，颗粒溶液扩散系数的改变。发现当宽度小于1.3 mm时，扩散系数随样品池宽度的减小线性增加，因此采用较窄壁间距的微量样品池，基于动态光散射技术对纳米颗粒粒度测量时，需对测量结果进行修正。

微量样品池内颗粒扩散系数减小的原因在于微量样品池壁间距较小，壁内表面的表面效应使溶液的有效黏滞系数增大，从而导致颗粒的扩散系数减小。值得指出的是，该现象是微小通道中布朗运动的普遍现象，在基于布朗运动的各种技术中都应考虑。

（

）：

[1]INTERNATIONAL ORGANIZATION FOR STANDARDIZATION（ISO）.Particle size analysis:photon correlation spectroscopy:ISO 13321[S].Geneve:1996.

[2]HOWARD B.The slow motion of a sphere through a viscous fluid towards a plane surface[J].Chemical Engineering Science，1961（16）:242-251.

[3]HOSODA M，SAKAI K，TAKAGI K.Measurement of anisotropic Brownian motion near an interface by evanescent light-scattering spectroscopy[J].Physical Review：E，1998，58（5）:6275-6280.

[4]LIU L L，CAI X S.Particle-size measurements in a micro-channel with image dynamic light scattering method[J].Procedia Engineering，2015（102）:905-910.

[5]BERNE B J，PECORA R.Dynamic light scattering with applications to chemistry，biology physics[M].New York:Dover Publications，2000:59-63.

[6]徐昊成，周风琴.毛细管内径大小对测量水的黏滞系数的影响[J].实验技术与管理，2013，30（5）:34-36.

[7]PFAHLER J，HARLEY J，BAU H，et al.Liquid transport in micron and submicron channels[J].Proceedings of Spie，1989，1167（89）:159-169.

[8]CHU B.Laser light scattering[M].New York:Dover Publications，2007:1-2.

[9]王乃宁.颗粒粒径的光学测量技术及应用[M].北京：原子能出版社，2000年.

[10]赵择卿.光散射技术[M].北京：纺织工业出版社，1989年.

[11]王志永，蔡小舒，徐呈泽，等.动态光散射图像法测量纳米颗粒粒度研究[J].光学学报，2014，34（1）:274-279.

[12]刘丽丽，蔡小舒，张杰，等.一种纳米颗粒粒度测量的快速图像动态光散射法研究[J].光学学报，2015，35（5）:361-367.

[13]WU X，LUO K，HAN P.Measurement of nano-particle diffusion in the simulated dynamic light scattering by contrast of dynamic images[C]//International Conference on Optical Instruments and Technology.International Society for Optics and Photonics，2015.

[14]XU J S，WU X B，QIU J，et al.Design of multiplexing photon correlator based on FPGA[J].Proceedings of SPIE-The International Sociaty for Opitical Engineering.2015：9623.

[15]夏辉，陈智全，李富石，等.拖曳效应对低相干动态光散射测量粒径的影响[J].光学学报，2010，30（8）:2257-2261.

[16]许继森.基于线阵CCD的动态光散射测量技术研究[D].广州：华南师范大学，2015.