复杂动态网络指数采样同步控制
陈刚,王信,肖伸平,罗昌胜
复杂动态网络指数采样同步控制
陈刚1, 2,王信1, 2,肖伸平1, 2,罗昌胜1, 2
(1. 湖南工业大学 电气与信息工程学院,湖南 株洲,412007; 2. 电传动控制与智能装备湖南省重点实验室,湖南 株洲,412007)
利用Lyapunov−Krasovskii泛函方法以及线性矩阵不等式方法,研究具有时变时滞复杂动态网络的指数采样同步控制问题。首先,建立包含更多时滞信息以及采样间隔信息的Lyapunov−Krasovskii泛函,运用更优积分不等式方法处理泛函导数中的积分二次型项,获得一种新的保证误差系统指数同步的稳定性判据。其次,基于此判据设计保证系统同步稳定的采样控制器。仿真结果表明:所得判据具有更小保守性,且采样控制器可行。
Lyapunov-Krasovskii泛函;复杂动态网络;指数采样同步控制
复杂动态网络(complex dynamic networks,CDNs)其实质是一种内节点的集合。其中各个节点对应确定的动态网络,而边缘连接线则代表网络之间的联系。近10年来,复杂动态网络受到人们极大关注,并且已经广泛地运用于实际系统如互联网、万维网、生态链、社交网络、电力系统网络、神经网络等中[1−3]。在众多网络动态行为中,同步性是一种典型的集体行为。而在人们的日常生活中,同步现象随处可见,如数字信号或模拟信号在网络中的传输。目前,已经提出许多同步问题如牵制同步、随机同步、脉冲同步、自适应同步、分布式同步等等。复杂动态网络的同步性不仅可以解释大量的自然现象,而且存在潜在利用价值。人们对复杂动态网络同步性进行了大量研究[4−14]。由于网络中信息传递速度的限制,时滞现象不可避免,而时滞的存在往往会使得系统变得不稳定、震荡,因此,对时滞现象的研究具有重要意义。ZENG等[15−16]对时滞现象进行了研究。对于含有时滞的复杂动态网络,研究其稳定状态下的最大允许时滞具有重要意义。在研究复杂动态网络同步控制问题中,已经提出多种控制方法,如状态观测器控制[17]、自适应控制[18]、脉冲控制[19]、牵制控制[20]、采样控制[21]等。另外,在实际应用中,控制策略要求数字反馈以及数字控制具有及时性、小型化、精确性以及低成本等特性,因此,复杂动态网络的同步控制具有很大的研究空间。采样控制作为一种实用、简洁的控制方法,其核心问题是采样区间的选取。可以通过Lyapunov−Krasovskii泛函方法,获得保证系统同步的稳定性判据,在此条件下,便可以得到最大采样间隔。同时,可以设计出保证系统同步的采样控制器[7−8, 11−12]。指数稳定性作为一种稳定规则,能够更加全面地解释系统稳定的特性。在众多稳定性研究方法中,Lyapunov−Krasovskii泛函方法与其他方法相比更加方便、直观。其核心问题包括2个方面:1) 构造更加优越的Lyapunov−Krasovskii泛函;2) 对其导数的界定。而在研究过程中,并没有找到一种固定的、无保守性的方法,在大多数情况下,都是依据个人经验,因此,仍需对Lyapunov−Krasovskii泛函方法进行研究。为此,本文作者在文献[8]的基础上,对于含有时变时滞的复杂动态网络构建含有更多时滞信息以及采样间隔信息的增广Lyapunov−Krasovskii泛函。值得注意的是,文献[12]中构造的含有采样点信息的泛函是不连续的,而在泛函中加上(t+1−),就能很好地避免这一问题。随后,对泛函求导,并利用积分不等式方法对导数中的积分二次型项进行界定,得到保证误差系统指数同步的充分性条件。为使获得的判据条件具有更小的保守性,采用ZENG等[22]推导的新自由矩阵积分不等式方法。基于此判据,设计出保证系统指数同步的采样控制器。最后,通过数值算例以及状态轨迹图证明所推导的判据具有更小的保守性,而且所得控制器是可行的。
1 问题描述
采用如下标号:矩阵上标“T”和“−1”分别表示转置矩阵以及逆矩阵;R和R×分别代表维向量和×维矩阵;矩阵>0代表矩阵是正定的;diag{1,…,b}表示块对角矩阵;和分别表示1个合适维度的零矩阵以及合适维度的单位矩阵;符号○表示张量积;sym{}代表矩阵T+;标记“*”表示块对阵矩阵中的对称项。
考虑下面的时变时滞复杂动态网络,此系统含有个耦合节点,每个节点都是1个维动态系统:
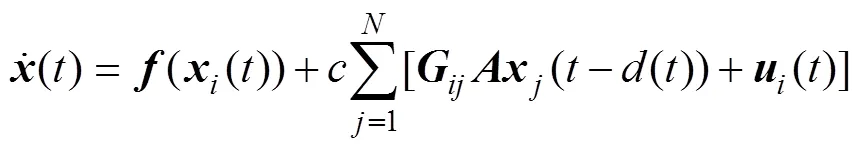
其中:= 1,2,…,;()以及()分别表示节点状态向量和控制输入;为恒定耦合强度;=(a)×∈R×,为连接节点之间的恒定内部耦合矩阵;=()×N,为网络拓扑结构的外部耦合组态矩阵。定义如下:若存在节点到节点(≠)的连接,则>0;否则,= 0。矩阵中的对角元素满足:

()表示离散时滞,并且满足以下条件:
其中:和都是正常数。
假设1为连续的向量函数且满足以下区间有界条件:


其中:和为合适维度的定值矩阵。

假设误差系统(4)的状态向量在时间点0<0<1<…<t<…是可测的,并且在采样间隔t≤<t+1中,(t)是存在的。于是,针对于误差系统(4),将采样状态反馈控制器设计成为以下形式:

其中:为采样反馈控制增益矩阵。假设在利用零阶保持函数生成的控制信号下,采样量是同步的,并且2个采样点之间满足:

其中:为正标量,代表最大采样间隔。这里并不要求采样间隔是周期性的,而只需满足控制器以式(5)的形式可行,且其最大采样间隔不大于。
随后,将(5)代入系统(4),可以得到下列误差系统:


其中:=1,2,…,。于是,式(7)可以写成


其中:=diag{1,2,…,};()=[1(),2(),…,()]T;(())=[(1()),(2()),…,(())]T。
在给出主要结论之前,下面先介绍几个引理。


其中:
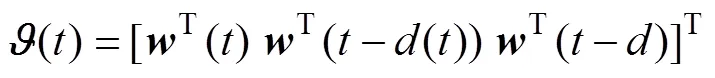
引理2[12]:对于所有对称正定矩阵以及可积函数{() |∈ [,]},有

引理3[22]:对于任意正定对称矩阵,2个标量和满足>>0,任意向量∈R,以及任意矩阵1,2∈R×,则
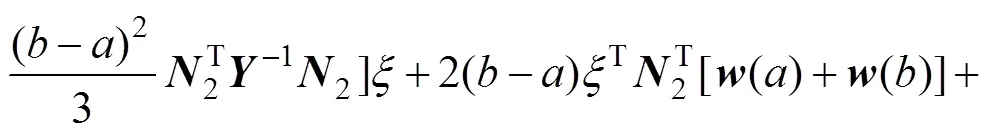
引理4[24]:对于任意合适维度矩阵1和2,1个对称矩阵3<0以及函数()∈[0,],满足

引理5[25]:存在合适维度的矩阵1,2和3,其中,1为对称矩阵,2为对称正定矩阵,则有
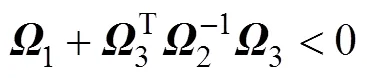
定义1 若误差系统(8)是指数稳定的,则复杂动态网络系统(1)是指数同步的。换言之,存在2个常数>0,>0,有

2 主要结果
利用Lyapunov-Krasovskii泛函方法以及线性矩阵不等式的形式推导并给出保证误差系统(8)指数渐进稳定的充分条件,并给出式(5)的采样控制器。为了使表达更加简洁,有下面的定义:
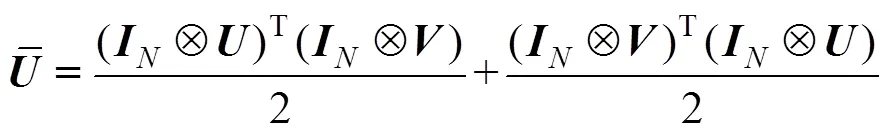





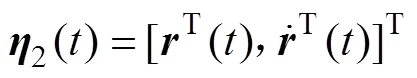
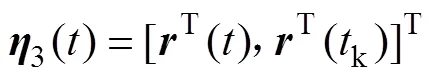
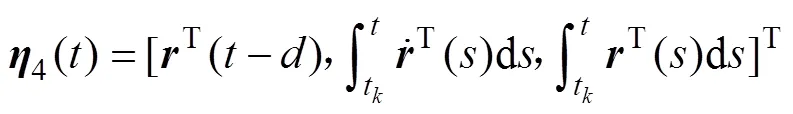

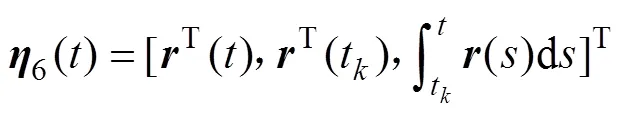


定理1:在条件(C1)下,给定正常数,,以及常数,若存在正定对称矩阵∈R2n×2n,∈ R2n×2n(=1, 2),∈R×(=1,2,3,4),1∈R2n×2n,2∈R3n×3n,对称阵∈R2n×2n,∈R×(= 1,3),5∈R×,正定对角阵∈R×(= 1,2),以及任意矩阵∈R×,2∈R×,∈R×(= 1,2),∈ R×(= 1,2,…,),∈R×(= 1,2,…,),∈R×(= 1,2,…,),∈R×(=1,2,3,4)。=diag{1,2,…,},=diag{1,2,…,},=diag{1,2,…,},且有


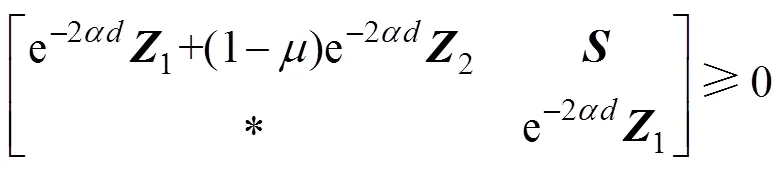
其中:
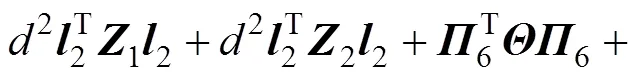

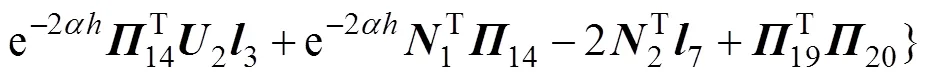
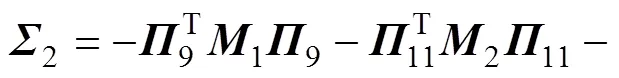
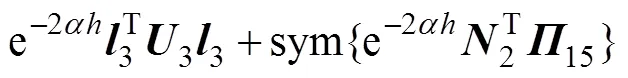


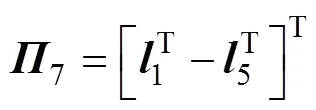

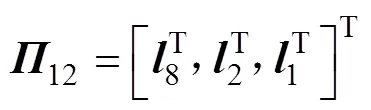

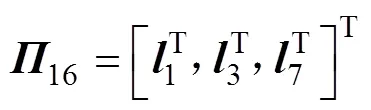
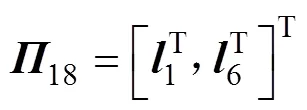
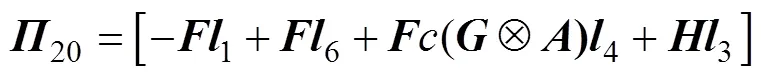
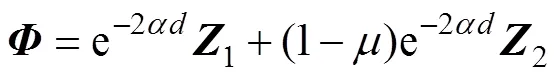


则误差系统(8)是指数稳定的,其衰减率为。另外,系统(8)中的可行控制增益矩阵求得为=−1。
证明:构建下面的增广泛函:

其中:

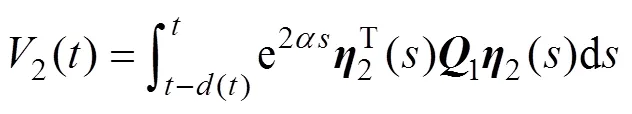

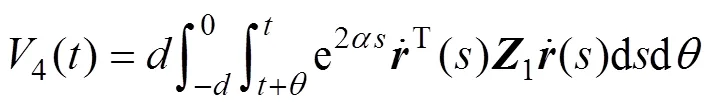
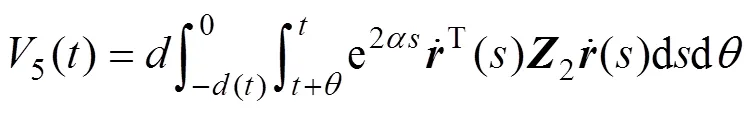
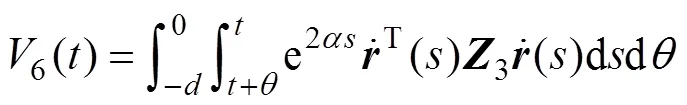





通过对()的各项求导,可以得到一系列矩阵以及积分式。而要求得线性矩阵不等式条件,其关键在于对导数中积分进行处理。下面将分别介绍对不同积分项的处理方法。
对4()和5()求导,将会产生下面2个积分二次型:


同样,对6()和7()求导,出现下面2种积分二次型:
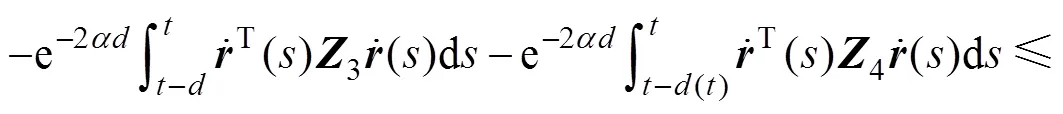

对8()求导,出现下面的二次型。依据基本不等式原理,当存在任意对称阵∈R2n×2n时,有下面不等式成立:


对7()利用同样的方法处理。进一步对10()导数中含有采样信息的积分项进行估计,当存在任意矩阵1和2时,有
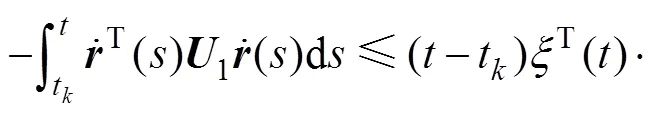

根据条件(6),式(17)可以写成


另一方面,存在常数>0,假设1中的条件(3)写成如下形式:
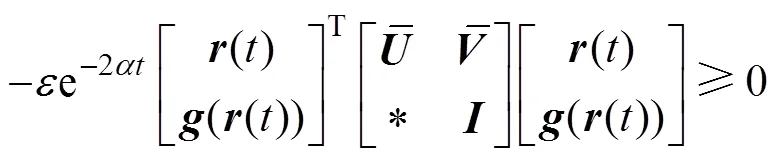
基于系统(8)的等式描述,可以引入2个合适维度的矩阵和,有下面的零项等式成立:

将(19)和(20)代入泛涵()的导数中,并将(14),(15),(16)和(18)应用于()的导数估计,于是,当t≤<t+1时,()的导数可以写成
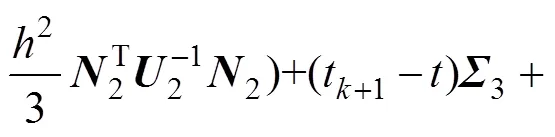

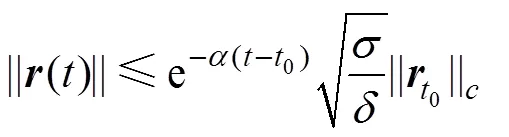
因此,误差系统(8)是指数稳定的,其衰减率为。根据定义1,系统(1)是指数同步的,其指数同步率为。证明结束。
注释1:相比于文献[8]中方法,本文构建1个新的增广Lyapunov−Krasovskii泛函,并且引入8和9,增加了更多的采样信息,使得所得判据具有更小的保守性。
注释2:若=0(即无线趋近于0),条件(10),(11)以及(12)可行,则系统(8)拥有足够小衰减率的指数同步,且据系统(8)中的可行控制增益矩阵求得=−1。

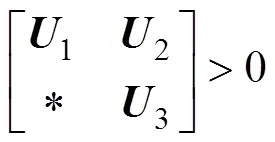


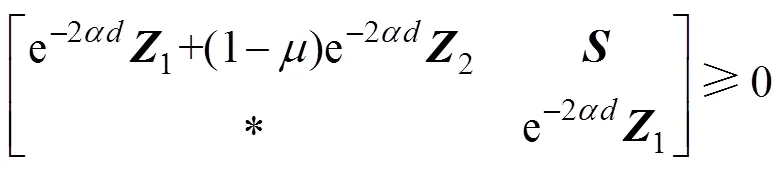

其中:
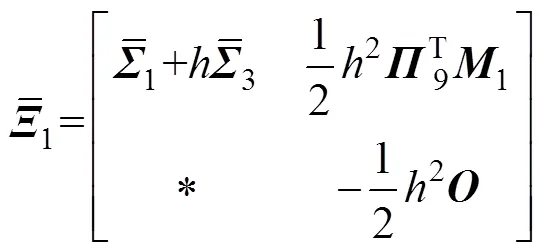
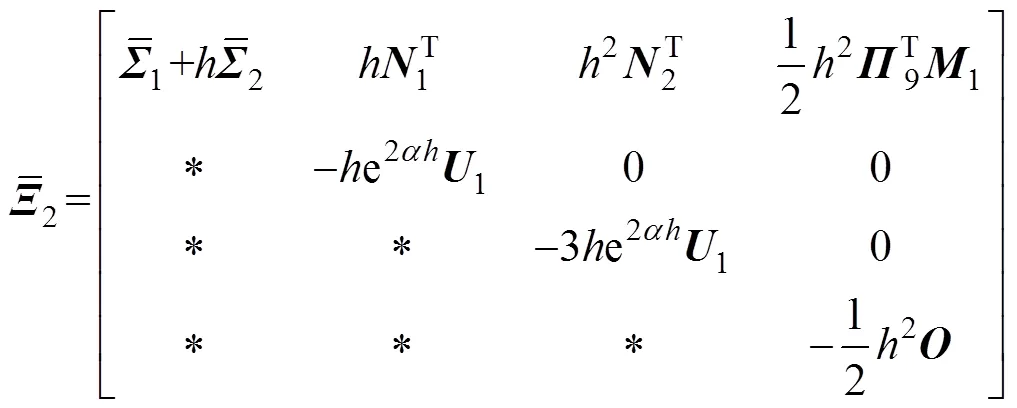

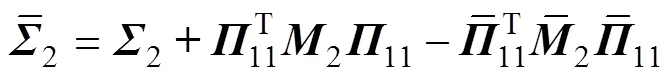
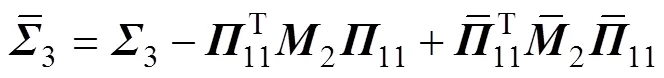
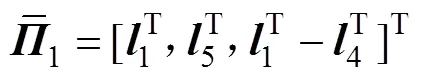
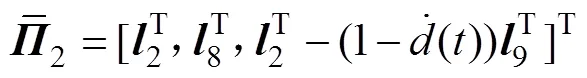


则误差系统(8)是指数稳定的,其衰减率为。且据系统(8)中的可行控制增益矩阵得=−1。
证明:构建增广泛函

其中:(),1()和9()含义见定理1,且

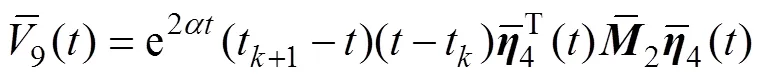
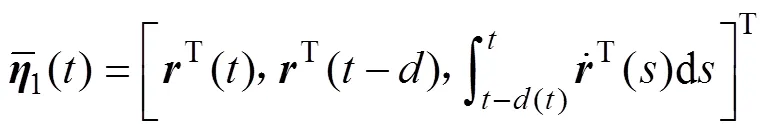

根据以上构建的泛函,并利用Lyapunov- Krasovskii泛函方法(与定理1同理),可以推导出定理2的结论。
注释4:若=0(也就是无限趋近于0),定理2可行,则系统(8)拥有足够小衰减率的指数同步,且据系统(8)中的可行控制增益矩阵求得=−1。
注释5:对比(C1)与(C2)这2种条件下的复杂动态网络指数同步条件,显然条件(C2)含有更多的时滞信息。其后的数值算理结果表明条件(C2)条件下所得的指数同步条件具有更小的保守性。
3 仿真实例
例1:对于误差系统(8),其内耦合矩阵与外耦合矩阵分别为
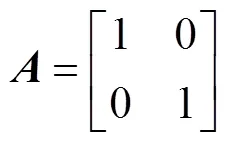
假设=0.25,=0.5,则非线性函数为
很显然,此函数满足条件(3),且

利用定理1与定理2中的充分判据,在 matlab工具箱中计算,可以得到在不同允许下的最大采样间隔,其计算结果见表1。从表1可以看出:与文献[6−10]中结果相比,本文所得最大采样间隔都明显增大;在文献[11]中,当=0.75时,其采样间隔大于本文结果。当=0.5时,本文所得采样间隔提高非常显著。同时,定理2与定理1相比,所得也提高,这说明耦合强度以及时滞导数条件对最大允许采样间隔的获得都有一定影响,同时说明本文所得判据具有一定优越性。

表1 定理1中不同c下的最大允许h
下面用仿真图来阐明所用方法的有效性。利用定理1,当=0.75,=0.944 9,=0.5,()=0.125+ 0.125 sin(4)时,利用Matlab中的SeDuMi工具箱可以计算得到采样控制器为:

在以上状态反馈控制器的基础上,当初始状态时,在该控制器下,无控制输入误差系统(8)的状态轨迹见图1,误差系统(8)的控制输入轨迹和状态轨迹分别见图2和图3。从图1~3可以看到:当无控制输入时,系统是发散的;而当系统增加本文推导的数字输入控制器时,状态轨迹则将趋近于平衡点。这证明了本文方法推导的数字控制器是可行的。
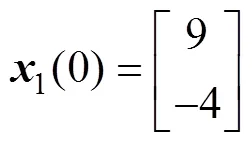
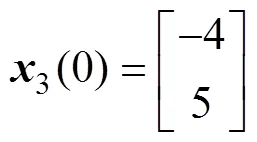
在定理2所得判据下,当=0.5,=1.121 2,=0,()=0.15+0.01cos(5)时,采样控制器为:
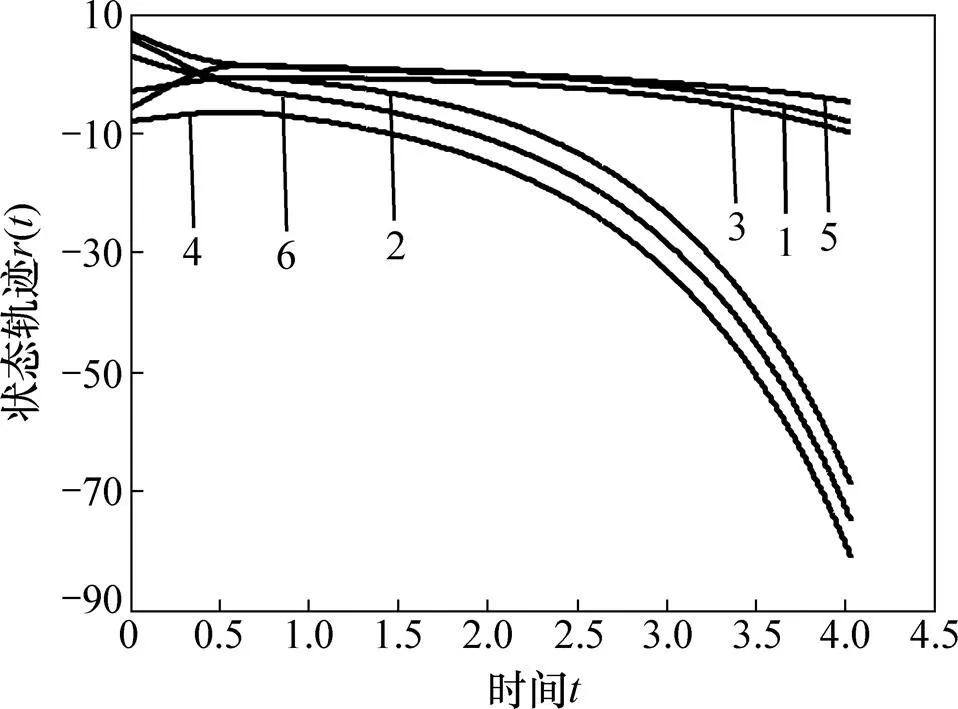
1—r11;2—r12;3—r21;4—r22;5—r31;6—r32。

1—r11;2—r12;3—r21;4—r22;5—r31;6—r32。

1—r11;2—r12;3—r21;4—r22;5—r31;6—r32。

初始状态为:
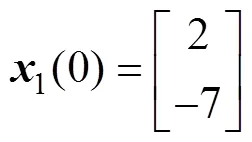
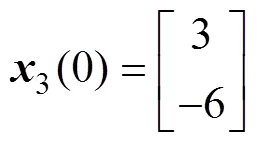
在该控制器以及初始状态下,无控制器下的状态轨迹见图4,控制输入轨迹见图5,误差系统(8)的状态轨迹见图6。同样,与之前的结论相同,对于发散系统,当增加了前面所推导的数字采样控制器时,系统轨迹以及输入轨迹都将趋于平衡点。这说明该控制器是可行的。
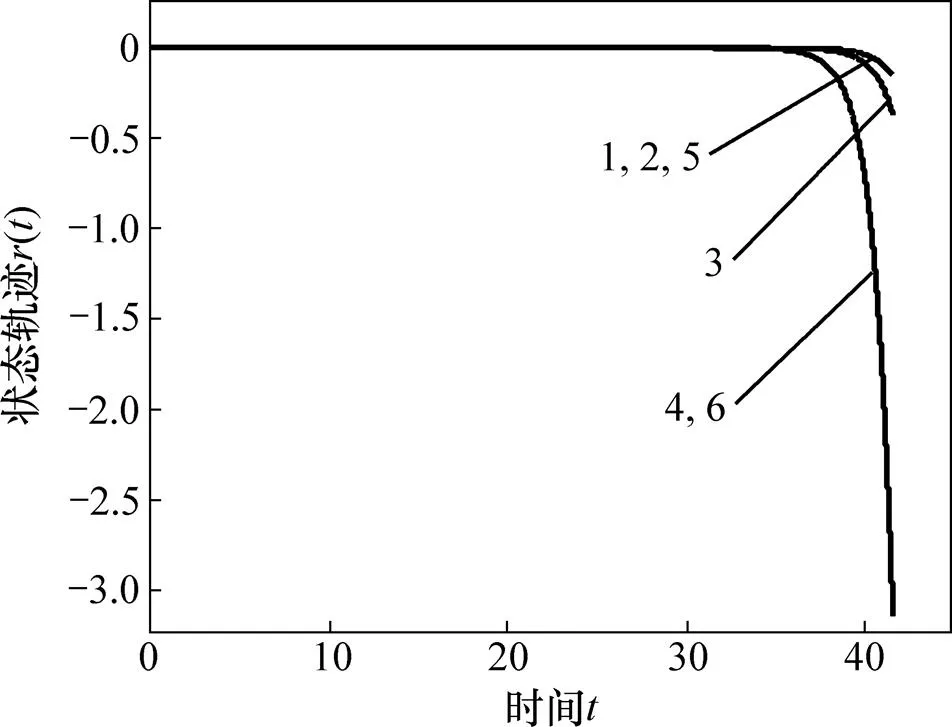
1—r11;2—r12;3—r21;4—r22;5—r31;6—r32。

1—r11;2—r12;3—r21;4—r22;5—r31;6—r32。
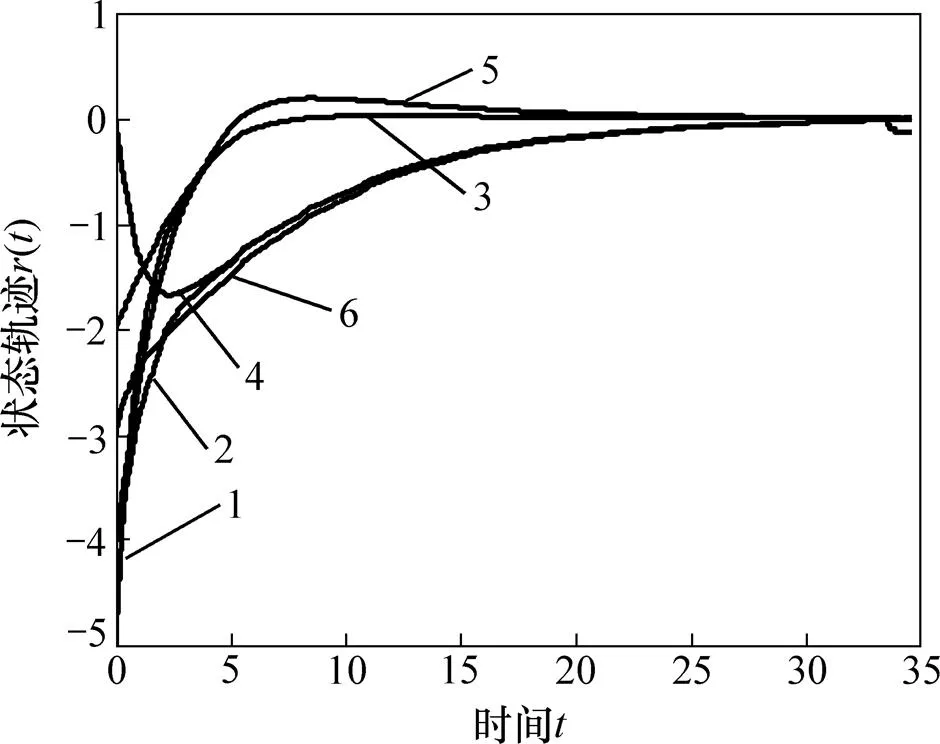
1—r11;2—r12;3—r21;4—r22;5—r31;6—r32。
4 结论
1) 对含有离散时滞的复杂动态网络进行研究,讨论其在采样控制下的指数同步问题,不仅得到保证网络指数同步的充分性条件,而且给出了采样控制器设计方法。
2) 基于减少稳定性条件保守性的目的,在泛函中增加采样信息,以及利用更优积分不等式估计泛函导数中的积分二次型数值对比,在所得定理条件下,可以获得更大采样间隔,表示本文的方法是有效的,并且系统轨迹图显示所得采样控制器能够实现系统的稳定性,证明了控制器设计方法可行。
[1] 张敏, 罗安. 一类非线性系统鲁棒控制及应用[J]. 中南大学学报(自然科学版), 2003, 34(2): 188−191.ZHANG Min, LUO An. Robust control for a class of nonlinear systems and its application[J]. Journal of Central South University (Science and Technology), 2003, 34(2): 188−191.
[2] YU Jianjiang, ZHANG Kanjian, FEI Shumin. Improved results on passivity analysis of discrete-time stochastic neural networks with time-varying delay[J]. Journal of Central South University(Science and Technology), 2009, 40(Z1): 63−67.
[3] BOCCALETTI S, LATORA V, MORENO Y, et al. Complex networks: structure and dynamics[J]. Physics Reports, 2006, 424(4/5): 175−308.
[4] LI Kun, GUAN Shuguang, GONG Xiaofeng, et al. Synchronization stability of general complex dynamical networks with time-varying delays[J]. Physics Letters A, 2008, 372(48): 7133−7139.
[5] LI Hongjie, YUE Dong. Synchronization stability of general complex dynamical networks with time-varying delays:a piecewise analysis method[J]. Journal of Computational & Applied Mathematics, 2009, 232(2): 149−158.
[6] LI Nan, ZHANG Yulian, HU Jianwen, et al. Synchronization for general complex dynamical networks with sampled-data[J]. Neurocomputing, 2011, 74(5): 805−811.
[7] WU Zhengguang, PARK J H, SU Hongye, et al. Exponential synchronization for complex dynamical networks with sampled-data[J]. Journal of the Franklin Institute, 2012, 349(9): 2735−2749.
[8] WU Zhengguang, SHI Peng, SU Hongye, et al. Sampled-data exponential synchronization of complex dynamical networks with time-varying coupling delay[J]. IEEE Transactions on Neural Networks & Learning Systems, 2013, 24(8): 1177−1187.
[9] WANG Junyi, ZHANG Huanguang, WANG Zhanshan. Sampled-data synchronization for complex networks based on discontinuous LKF and mixed convex combination[J]. Journal of the Franklin Institute, 2015, 352(11): 4741−4757.
[10] SU Lei, SHEN Hao. Mixed H∞/passive synchronization for complex dynamical networks with sampled-data control[J]. Applied Mathematics & Computation, 2015, 259: 931−942.
[11] LIU Yajuan, GUO Baozhu, PARK J H, et al. Nonfragile exponential synchronization of delayed complex dynamical networks with memory sampled-data control[J]. IEEE Transactions on Neural Networks & Learning Systems, 2016, 29(1): 118−128.
[12] LIU Yajuan, LEE S M. Improved results on sampled-data synchronization of complex dynamical networks with time-varying coupling delay[J]. Nonlinear Dynamics, 2015, 81(1/2): 931−938.
[13] WANG Jianan. New synchronization stability criteria for general complex dynamical networks with interval time-varying delays[J]. Neural Computing & Applications, 2017, 28(4): 805−815.
[14] WANG Jianan, ZENG Chan, WEN Xinyu. Synchronization stability and control for neutral complex dynamical network with interval time-varying coupling delay[J]. Circuits Systems & Signal Processing, 2017, 36(2): 559−576.
[15] ZENG Hongbing, HE Yong, WU Min, et al. Free-matrix-based integral inequality for stability analysis of systems with time-varying delay[J]. IEEE Transactions on Automatic Control, 2015, 60(10): 2768−2772.
[16] ZENG Hongbing, HE Yong, WU Min, et al. New results on stability analysis for systems with discrete distributed delay[J]. Automatica, 2015, 60(C): 189−192.
[17] JIANG Guoping, TANG W K, CHEN Guanrong. A state-observer-based approach for synchronization in complex dynamical networks[J]. IEEE Transactions on Circuits & Systems, 2006, 53(12): 2739−2745.
[18] LI Xiaojian, YANG Guanghong. Adaptive fault-tolerant synchronization control of a class of complex dynamical networks with general input distribution matrices and actuator faults[J]. IEEE Transactions on Neural Networks & Learning Systems, 2017, 28(3): 559−569.
[19] YANG Xinsong, CAO Jinde, LU Jianquan. Stochastic synchronization of complex networks with nonidentical nodes via hybrid adaptive and impulsive control[J]. IEEE Transactions on Circuits & Systems, 2012, 59(2): 371−384.
[20] WANG Jinliang, WU Huaining, HUANG Tingwen, et al. Pinning control for synchronization of coupled reaction-diffusion neural networks with directed topologies[J]. IEEE Transactions on Systems Man & Cybernetics Systems, 2015, 46(8): 1109−1120.
[21] WU Zengguang, SHI Peng, SU Hongye, et al. Exponential synchronization of neural networks with discrete and distributed delays under time-varying sampling[J]. IEEE Transactions on Neural Networks & Learning Systems, 2012, 23(9): 1368−1376.
[22] ZENG Hongbing, TEO K L, HE Yong, et al. Sampled-data synchronization control for chaotic neural networks subject to actuator saturation[J]. Neurocomputing, 2017, 260: 25−31.
[23] PARK P G, KO J W, JEONG C. Reciprocally convex approach to stability of systems with time-varying delays[J]. Automatica, 2011, 47(1): 235−238.
[24] ZHANG Yijun, YUE Dong, TIAN Engang. New stability criteria of neural networks with interval time-varying delay: a piecewise delay method[J]. Applied Mathematics and Computation, 2009, 208(1): 249−259.
[25] RAKKIYAPPAN R, LATHA V P, ZHU Quanxin, et al. Exponential synchronization of Markovian jumping chaotic neural networks with sampled-data and saturating actuators[J]. Nonlinear Analysis Hybrid Systems, 2017, 24: 28−44.
Sampled-data exponential synchronization for complex dynamical networks
CHEN Gang1, 2, WANG Xin1, 2, XIAO Shenping1, 2, LUO Changsheng1, 2
(1. School of Electrical and Information Engineering, Hunan University of Technology, Zhuzhou 412007, China; 2. Key Laboratory for Electric Drive Control and Intelligent of Hunan Province, Zhuzhou 412007, China)
By using Lyapunov−Krasovskii functional method and linear matrix inequality method, the problem of sample-data exponential synchronization for complex dynamic networks with time-varying delays was studied. Firstly, the Lyapunov−Krasovskii functional with more information and the sampling interval delay information was constructed. Then, the preferable integral inequality methods were used to estimate the integral quadratic terms among derivative of Lapunov−Krasovskii functional and a new criterion was formulated to ensure the exponential synchronization of the error system. Secondly, a sampling controller was designed based on this criterion to ensure the synchronization of the system. The simulation results show that the derived synchronization criterion is less conservative and it is feasible.
Lyapunov−Krasovskii functional; complex dynamic networks; sampled-data exponential synchronization
10.11817/j.issn.1672−7207.2018.12.013
TP273
A
1672−7207(2018)12−2993−09
2018−01−10;
2018−03−15
湖南省自然科学基金资助项目(2018JJ4075);国家自然科学基金资助项目(6167225, 61304064)(Project(2018JJ4075) supported by the Natural Science Foundation of Hunan Province; Projects(6167225, 61304064) supported by the National Natural Science Foundation of China)
陈刚,博士,副教授,从事时滞系统、鲁棒控制研究;E-mail:drchengang@163.com
(编辑 陈灿华)

