灰色关联度优化钛合金盘铣开槽工艺参数

李志山, 史耀耀, 辛红敏, 赵涛, 杨程

(西北工业大学 现代设计与集成制造技术教育部重点实验室, 陕西 西安 710072)

整体叶盘是航空发动机的关键零部件，因工作条件多为高温、高压、高转速等恶劣工况，一般采用钛合金、高温合金等难加工材料来制造，所以给整体叶盘的制造加工带来众多困难。目前，整体叶盘通道加工工艺技术以数控铣削为主，铣削工艺主要有2种，分别为侧铣和插铣。侧铣开槽加工是采用球头铣刀或圆柱铣刀进行侧铣行切，利用高精度数控机床的五轴联动功能，刀具侧切削刃可直接加工至叶片直纹型面尺寸。插铣开槽加工又称Z轴铣削法，在加工过程中利用刀具底部的切削刃沿轴线方向做进给运动，实现钻、铣组合切削[1]。但整体叶盘通道深而窄，开敞性差，且叶片曲率变化大，必须使用细长刀具，所以在刀具侧铣加工过程中径向受力较大，振动明显，严重时甚至出现断刀现象，进而加剧刀具磨损，降低加工效率。为了解决以上问题，本文提出了一种新的整体叶盘通道开槽加工工艺，即盘铣。研究表明，盘铣能有效提高整体叶盘的开槽效率，是插铣的3倍左右，侧铣的7倍左右[2-3]。

对于一般的加工而言，工件和夹具是设定好的，刀具和机床的结构优化起来成本又太高，所以为了得到更优的切削效果，优化工艺参数是比较可行的方法。参数优化的方法按原理不同可以分为2类[4]：数学规划法和试验方法。数学规划法又分为动态规划、线性规划和非线性规划。试验方法包括因素设计法、响应曲面法、田口法、灰色关联法、支持向量机法、神经网络法等。国内外的学者分别采用不同方法对工艺参数优化进行了深入地研究，也积累了大量的成果。

刘建峰[5]以遗传算法为基础，采用模拟退火遗传算法进行微细铣削表面粗糙度值和铣削力的单目标和多目标优化，通过对2种算法的优化结果进行对比，得出结论：模拟退火遗传算法优化工艺参数更加可靠。马超[6]以铣削加工为基础，选取表面加工质量和机床稳定性为优化目标，采用遗传算法和粒子群算法的智能优化算法对工艺参数进行优化，并以数控铣床为例验证了优化结果的正确性。陈建岭[7]以生产效率最大化和刀具寿命消耗最小为目标，采用多目标多约束的NSGA-Ⅱ改进算法，实现了高速铣削钛合金的工艺参数优化。Cao等[8]以整体叶片为加工对象，采用神经网络和遗传算法相结合的方法对切削参数进行优化，优化结果表明：此种方法不仅能有效降低优选工艺参数的时间成本，而且优化后的工艺参数能有效提高整体叶片的加工质量。黄天然等[9]采用支持向量机法对盘铣钛合金表面残余应力的铣削参数进行了优化，首先设计正交实验，基于实验数据建立支持向量机模型，结果证明支持向量机法建立的回归模型比传统的回归方法更有优势，适用于小样本多因素多水平实验建模。孙玉文[10]设计正交实验，建立表面粗糙度模型，利用响应曲面法对等值线和响应曲面图进行分析，最终确定最优铣削参数。

Kumar等[11-12]采用灰色关联分析法对电火花线切割加工钛合金时的性能参数(峰值电流、脉冲上升时间和脉冲下降时间)进行了多目标优化，结果表明通过平衡材料去除率、电极损耗比和表面粗糙度多目标之间的关系得到的加工参数可以更好地保证加工性能。Manikandan等[13]选取材料去除率和阴极外表面与加工部件切削面的间距为优化目标，工艺参数有进给速率、电解质流动速率和电解质浓度，分别采用田口法、信噪比法、方差分析法和灰色关联分析法对电化学钻铣钛合金TC4时的工艺参数进行优化。Vaxevanidis等[14]以车削钛合金TC4时的主切削力和表面粗糙度为优化目标，选取主轴转速、进给速率和切削深度设计27组正交数据表进行实验，并以方差分析法分析实验数据，最后以人工神经网络法模拟这些数据进行参数优化，结果证明由实验方法和神经网络法相结合的方法得到的工艺参数不仅可以有效地节省成本和时间，还改善了车削加工后的零件表面质量。Nandakumar等[15]为了平衡材料去除率和表面粗糙度之间的关系，采用响应曲面法对电火花线切割钛合金TC4时工艺参数进行了优化，结果表明响应曲面法对于建立统计模型和进行图表分析是一个强有力的工具，在优化参数方面具有较明显的优势。Gunay等[16]以田口法设计L9组正交实验，选取铣削力Fc和表面粗糙度为优化目标，通过计算实验数据的信噪比数值来选用最优的工艺参数和刀尖圆弧半径。

在优化工艺参数时，多目标优化可以做到多目标之间的平衡，比单目标优化更具有价值。灰关联分析可以同时兼顾多个目标，对目标侧重点不同，可得到不同的工艺参数优化结果[17-18]，因而得到了广泛的应用。将盘铣应用于整体叶盘的开槽加工是一种新工艺，它的突出优势在于能有效提高开槽加工效率。但由于盘铣开槽过程中铣削力大、铣削温度高，造成刀具磨损严重，降低刀具使用寿命，而且已加工表面会形成较深的塑性变形层。本文以材料去除率、刀具寿命和残余应力层厚度为优化目标，基于灰色关联分析将多目标优化转化为单目标优化，建立工艺参数与灰色关联度的预测模型，进而得到工艺参数的优化方案。

1 材料与试验

材料

本次试验中选用的钛合金材料TC4(Ti-6Al-4V)经过热处理及高温锻造，其测试硬度为33～35 HV，样品尺寸：120 mm×60 mm×60 mm，其化学成分及力学性能见表1和表2，微观组织结构见图1。

表1 TC4钛合金化学成分

表2 TC4钛合金力学性能

图1 TC4钛合金微观结构图

刀具

在本次试验中选用的是由株洲钻石切削刀具股份有限公司生产制造的整体错齿三面刃盘铣刀。刀片材料为硬质合金YG6，它的组成成份为94%的WC和4%的Co，盘铣刀的几何参数如表3所示。

表3 盘铣刀几何参数

试验条件

选用XH716立式加工中心做为铣削试验平台。为了延长刀具的使用寿命，采用顺铣铣削方式，乳化液作为冷却液。本文所有的研究内容是为了将盘铣工艺应用于整体叶盘开槽加工所进行的探索性研究，由于将盘铣应用于整体叶盘的开槽加工是一种新工艺和新思路，并没有相关的工艺参数可以参考,只能根据前期的研究成果及现有加工设备的工况进行参数选定。具体的工艺参数的确定方法如下：盘铣开槽切削效率高、盘铣刀直径大，且在高效强力复合铣装备中，所设计盘铣主轴头的最高主轴转速为100 r/min，所以本次试验中将主轴转速最大值设为100 r/min；切削厚度则根据整体叶盘通道特征确定，最后根据机床可承受的振动范围选择进给速度。设计正交试验,试验参数如表4所示。

表4 盘铣工艺参数

测量方法

1)刀具寿命

采用后刀面最大磨损量VBmax作为刀具磨损评价指标，每次铣削长度60 mm后将刀具放在表面质量测量仪下观察后刀面磨损值，当超过3个以上的刀齿的磨损量达到0.3 mm时停止试验，认为盘铣刀失去切削功能。由于盘铣刀造价高，本次试验中刀具数量有限，所以在测量刀具寿命时没有考虑刃磨次数。

2)材料去除率按(1)式计算

(1)

式中,Q为材料去除率；Vf为进给速度；ap为切削深度；ae为切削厚度。因试验中盘铣刀厚度为20 mm，此处ae取20 mm。

3)变质层厚度

此处选用残余应力层厚度做为变质层的评价参数。表面下残余应力测试采用电化学腐蚀法，具体方法为采用电解抛光机对铣削表面进行电解剥层，剥层时间约为15 s，用千分尺控制每次剥层的厚度，约为10～20 μm，将每次剥层后的TC4铣削表面在LXRD MG残余应力测试分析系统下进行残余应力测试，重复以上步骤，直到测得的残余应力值为0为止。

试验结果见表5，因素A,B,C分别表示主轴转速nr/min、切削深度ap/mm、进给速度vf(mm·min-1)，Q为材料去除率，T为刀具寿命，Hs为残余应力层厚度，1,2,3分别代表不同因素的不同工艺水平。

表5 三因素三水平参数及实验结果

2 试验结果分析

2.1 灰色关联分析

2.1.1 试验数据处理

为了使不同单位的试验数据具有可比性，需对收集到的原始数据进行变换和处理，消除其量纲。在盘铣开槽加工过程中，刀具寿命和材料去除率越大越好，属于效益型；而残余应力层厚度则越小越好，属于成本型，分别采用效益型和成本型多指标序列变换公式(2)和(3)对表5中的数据进行变换，变换结果见表6。

效益型:

(2)

成本型:

(3)

式中，yi(k)为变换后数列;xi(k)为原始数列;i为试验次数;k为优化目标,此处为材料去除率、刀具寿命、残余应力层厚度。

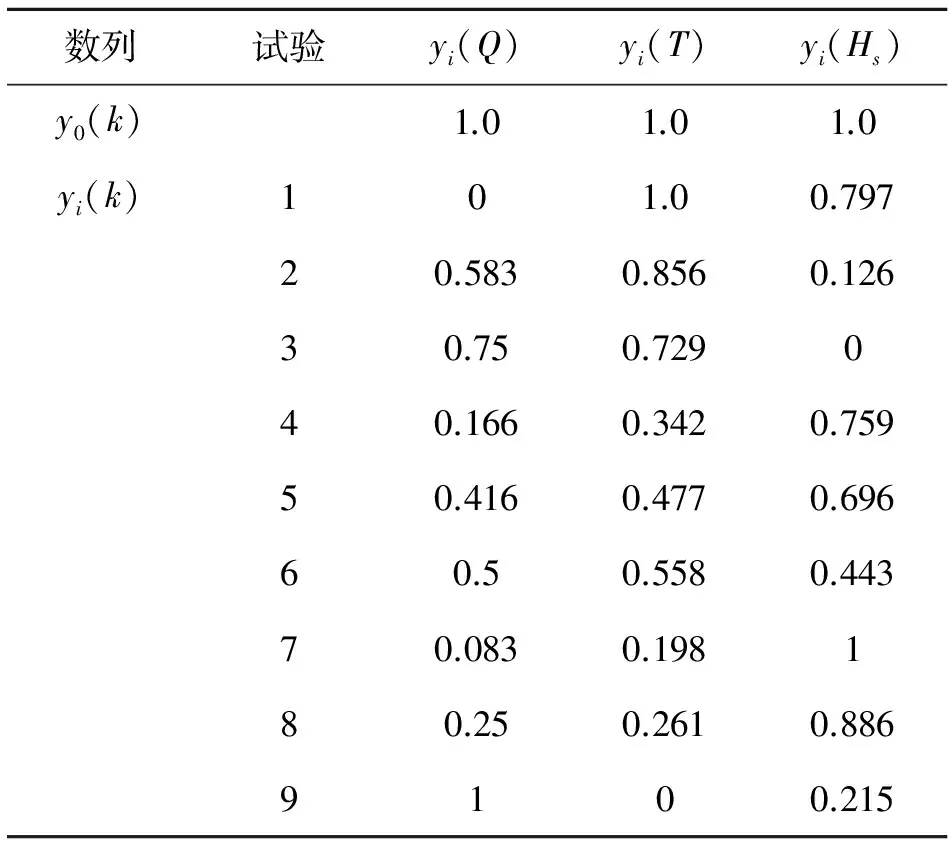
表6 试验数据变换结果

2.1.2 计算灰色关联系数

关联性实质上是曲线间几何形状的差别,因此,可以将曲线差值的大小,作为关联程度的衡量尺度,灰色关联系数计算公式如(4)式[19]。

(4)

由(4)式计算灰色关联系数见表8。

2.1.3 响应权重计算

主成分分析(principal component analysis, PCA)是将数据从高维空间变换到低维空间的降维技术。通过主成分分析可以定量知道各个因子对响应的影响程度或者贡献率,本文利用其计算材料去除率、刀具寿命和残余应力层厚度对灰色关联度的贡献率(即影响权重),步骤如下:

Step1 建立多种质量特征的原始序列,xi(j),i=1,2,…,m;j=1,2,…,n。

(5)

式中，m为试验次数;n为目标响应数;x为每个目标响应的灰色关联系数,本文中m=9,n=3。

Step2 计算相关系数数组:

相关系数数组计算方法如(6)式所示:

(6)

式中，cov(xi(j),xi(l))为xi(j)和xi(l)的协方差,j,l=1,2,…,n;σxi(j)为xi(j)的标准差;σxi(l)为xi(l)的标准差。

Step3 计算特征值和特征向量:

通过求解特征方程(见公式(8)),得到特征值λk,k=1,2,,,n,并将其按照从大到小顺序排列,即λ1≥λ2≥…≥λn≥0。

|λkIm-R|=0

(7)

式中，Im为单位矩阵。

Step4 计算主成分贡献率和累计贡献率:

主成分贡献率αk和累计贡献率Nk分别如公式(8)和公式(9)所示:

(8)

(9)

一般当Nk≥85%时,则λ1,λ2, …分别称之为第一主成分、第二主成分,以此类推。

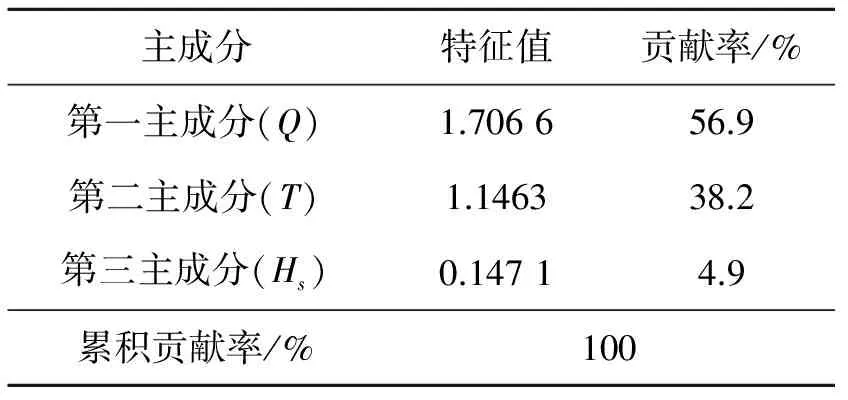
表7 主成分分析结果

利用表8中的灰色关联系数,通过(6)式计算系数矩阵R,然后分别利用公式(7)、公式(8)和公式(9)计算特征值、贡献率和累计贡献率,结果见表7。由表7可知,第一主成分为材料去除率Q,第二主成分为刀具寿命T,第三主成分为残余应力层厚度Hs,其贡献率分别为56.9%,38.2%,4.9%。

对于盘铣开槽加工来说,材料去除率Q贡献率最大,进而说明提高效率是盘铣开槽加工的最终目的。

2.1.4 计算灰色关联度

灰色关联度是灰色关联系数的加权和,其计算公式如(10)式所示:

(10)

由表7可知(10)式中的β1=0.569,β2=0.382,β3=0.049,灰色关联度的计算结果见表8。

表8 灰色关联系数与灰色关联度

灰色关联度越大,相应的响应目标越好,由表8可知试验号9所对应的响应目标最好。与之相对应,当参数水平所对应的平均灰色关联度最大时,所对应的目标响应最好[20]。由公式(11),计算各工艺因素在各水平下的平均灰色关联度;根据公式(12)计算各工艺因素各水平平均灰色关联度的最大差值δmax,计算结果见表9。

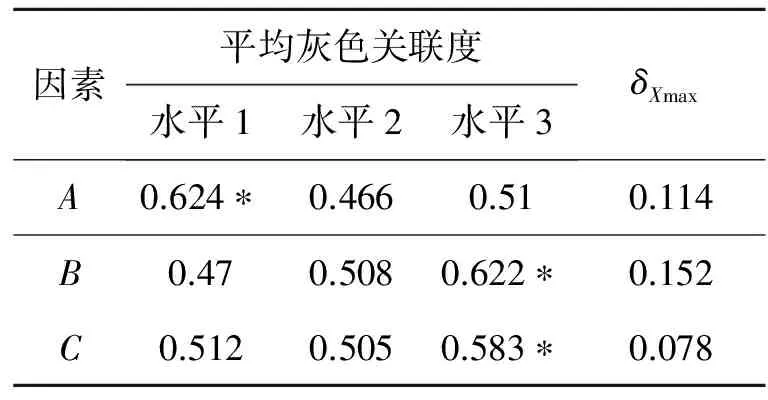
表9 各因素各水平的平均灰色关联度

(11)

(12)

表9中带“*”的平均灰色关联度最大,即为各因素的最佳水平,主轴转速的最佳水平为40 r/min,切削深度的最佳水平为9 mm, 进给速度的最佳水平为100 mm/min。

由灰色系统相关理论知,δXmax代表各工艺参数对考察指标的影响程度。由表9可知,因素B即切削深度对目标响应的影响最大,主轴转速次之,进给速度的影响最小。

2.2 工艺参数优化

2.2.1 建立优化模型

为进行盘铣开槽加工工艺参数优化,需构建灰色关联度和工艺参数间的关系。通常采用响应曲面法中的二阶数学回归模型来表示目标响应和输入因子之间的关系。灰色关联度(G)与盘铣开槽加工工艺参数间的二阶回归方程如(13)式所示:

(13)

利用Minitab软件对试验数据进行回归分析,建立灰色关联度的预测模型如(14)式所示。灰色关联度的预测值和计算值对比如图2所示。由图2可知,灰色关联度的预测值与计算值非常接近,平均偏差为1.39%,表明预测值和计算值之间无显著差异。模型的方差分析结果如表10所示,其中R-Sq表示回归模型与数据的吻合度,R-Sq(adj)=96.16%表明模型与试验数据吻合度很好;R-Sq和R-Sq(adj)非常接近,表明模型非常可靠。图3为预测模型的残差图,图3中所有残差都在0值附近随机分布,无异常点出现,说明预测模型对观测值的拟合度良好。因此,基于正交试验和灰色关联分析的回归模型可作为灰色关联度的预测模型。

(14)

图2 灰色关联度预测值与计算值对比图

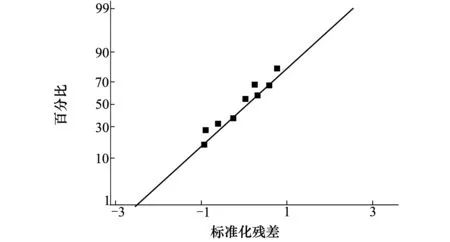
图3 灰色关联度预测模型的残差图

参数自由度平方和均方FF0．01(3，5)F0．05(3，5)显著性回归平方和70．1082520．01546529．5912．065．41是残差平方和10．0615270．020509总和8SD=0．0228619R⁃Sq=99．52%R⁃Sq(adj)=96．16%

2.2.2 影响规律分析

利用主效应分析来研究盘铣开槽加工工艺参数对材料去除率、刀具寿命、残余应力层厚度和灰色关联度的影响规律,如图4所示。图4表示工艺参数n,ap和vf单独变化时响应的变化趋势,其中X轴表示每个工艺参数的3个水平,Y轴表示每个响应的数值大小。

由图4a)可知,对于材料去除率,切削深度斜率最大,表明切削深度对材料去除率的影响最大,而主轴转速和进给速度的影响相对较小。其中,材料去除率随着主轴转速的增加呈现先减小后增大的趋势,随着切削深度和进给速度的增大而增大。因此要想使材料去除率达到最大,应取n=100 r/min,ap=9 mm,vf=100 mm/min,称之为max-Q参数组合。

由图4b)可知,对于刀具寿命来说,主轴转速的斜率最大,表明主轴转速对刀具寿命影响最为显著,切削深度和进给速度的影响则不明显,其中切削深度的影响由于较小,在此处可忽略不计。刀具寿命随着主轴转速和进给速度的增加而减小,因此要使刀具寿命达到最大,应取工艺参数n=40 r/min,ap=3 mm,vf=60 mm/min,称之为max-T参数组合。

由图4c)可知,切削深度对残余应力层厚度的斜率最大,表明其对残余应力层厚度影响较大,主轴转速次之,进给速度最不显著。残余应力层厚度随着主轴转速的增加而增加,随着切削深度和进给速度的增大而减小,所以要想获得较浅的残余应力层,应取工艺参数n=100 r/min,ap=3 mm,vf=60 mm/min,称之为min-Hs参数组合。

由图4d)可知,对于灰色关联度,主轴转速和切削深度的影响较大,进给速度的影响相对较小,其中灰色关联度随着主轴转速和进给速度的增大呈现先减小后增大的趋势,随着切削深度的增大而增大。

图4 主效应分析结果

从上述分析发现,Q,T和Hs的灰色关联系数均为参数依赖性响应,灰色关联度(GRG)亦为参数依赖性响应,且工艺参数对灰色关联度的影响是工艺参数对各响应的灰色关联系数影响的加权和。因此可以通过灰色关联度的变化来体现工艺参数对各响应目标的影响规律,对灰色关联度的优化可实现对材料去除率、刀具寿命和残余应力层厚度的整体优化。

2.2.3 优化结果

利用Minitab软件中的响应优化器对所建立的灰色关联度预测模型进行分析,得到灰色关联度的最优解为G=0.742 4,所对应的工艺参数组合为:n=100 r/min,ap=9 mm,vf=86 mm/min,如图5a)所示。同理,利用等权方法,即公式(10)中取β1=0.333,β2=0.333,β3=0.333,获得的灰色关联度最优解为G*=0.715,所对应的工艺参数组合为:n=40 r/min,ap=3 mm,vf=76 mm/min,称之为等权优化参数组合,如图5b)所示。

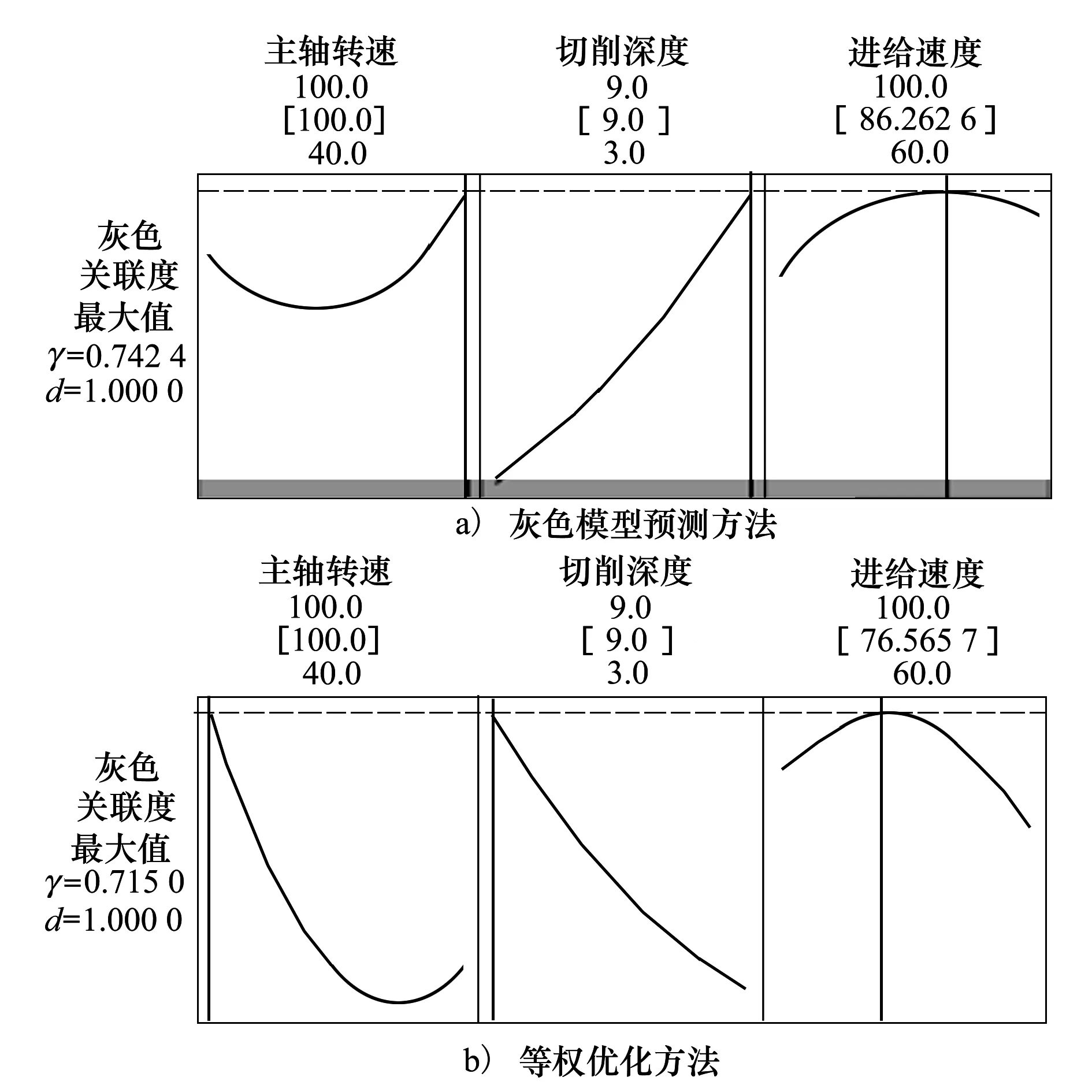
图5 工艺参数优化结果

2.2.4 试验验证

采用文中所提出的灰色模型预测方法得到的工艺参数组合,进行盘铣开槽加工试验;同时将等权优化方法得到的工艺参数组合做为对比试验组。图6为盘铣开槽加工试验加工现场图,表11为试验验证结果。试验结果表明,灰色模型优化方法所对应的工艺参数在材料去除率方面具有绝对的优势,约是等权优化方法所对应工艺参数的3倍左右;如果从刀具寿命和残余应力层厚度方面分析的话,等权优化方法所对应的工艺参数可得到较长的刀具寿命和较浅的残余应力层,相对于灰色模型分析法所对应的工艺参数,刀具寿命提高1倍左右,残余应力层厚度由于相差不大,这里暂不做对比分析。虽然2种方法分析出来的结果各有优势,但结合盘铣开槽加工的应用环境可知,材料去除率是首要考虑的问题,所以在选取工艺参数方面应优先保证材料去除率,其次才是刀具寿命。由此说明,等权优化方法应用在盘铣开槽加工过程中具有一定的局限性,而根据试验数据来计算每个响应对多目标优化响应影响权重的方法更为可靠有效。

图6 盘铣开槽试验加工现场

参数组合n/(r·min-1)ap/mmvf/(mm·min-1)Q/(mm3·min-1)T/minHs/μm灰色模型方法10098615．4810．8252等权优化方法403764．5619．5230

3 结 论

针对盘铣开槽过程的材料去除率、刀具寿命、残余应力层厚度,提出一种多目标优化方法。采用主成分分析法计算各响应对灰色关联度的影响权重,利用响应曲面法建立多目标预测优化模型,通过主效应法分析各参数分别对材料去除率、刀具寿命、残余应力层厚度和灰色关联度的影响规律,确定工艺参数优化方案,并获得了最优的工艺参数组合。通过研究发现:主轴转速和切削深度对灰色关联度的影响较大,进给速度的影响相对较小;灰色关联度随着主轴转速和进给速度的增大呈现先减小后增大的趋势,随着切削深度的增大而增大;材料去除率、刀具寿命、残余应力层厚度难以同时达到最优,通过灰色关联度的优化可以实现对二者的整体优化。试验结果表明:基于等权的灰色关联分析在盘铣开槽工艺参数优化方面具有一定的局限性,而本文所提出的加权灰色关联分析法具有显著的优越性。

[1] Jeong H K, Yusuf A. Time Domain Model of Plunge Milling Operation[J]. International Journal of Machine Tools and Manufacture, 2007, 47(9): 1351-1361

[2] Zhao P B, Shi Y Y. Adaptive Sliding Mode Control of the a-Axis Used for Blisk Manufacturing[J]. Chinese Journal of Aeronautics, 2014, 27(3): 708-715

[3] Zhao P B, Shi Y Y. Robust Control of the a-Axis with Friction Variation and Parameters Uncertainty in Five-Axis Cnc Machine Tools[J]. Proceeding of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2014, 228(14): 2545-2556

[4] Rao R V, Kalyankar V D. Optimization of Modern Machining Processes Using Advanced Optimization Techniques: a Review[J]. International Journal of Advanced Manufacturing Technology, 2014, 73(5/6/7/8): 1159-1188

[5] 刘建峰. 基于模拟退火遗传算法的微细铣削加工参数优化[D]. 哈尔滨: 哈尔滨工业大学, 2010

Liu Jianfeng. Parameters Optimization of Micro-End-Milling Based on Simulated Annealing Genetic Algorithm[D]. Harbin, Harbin Institute of Technology, 2010 (in Chinese)

[6] 马超. 基于加工动力学模型的工艺参数优化研究[D]. 武汉: 华中科技大学, 2012

Ma Chao. Optimization Study on the Processing Parameters Based on the Cutting Dynamic Model[D]. Wuhan, Huazhong University of Science and Technology, 2012 (in Chinese)

[7] 陈建岭. 钛合金高速铣削加工机理及铣削参数优化研究[D]. 济南: 山东大学, 2009

Chen Jianling. Research on Milling Machining Mechanism and Milling Parameters Optimization of Titanium Alloy with High Speed[D]. Jinan, Shandong University, 2009 (in Chinese)

[8] Cao Y, Dong X J, Du J. Optimal Selection of Cutting Parameters in Blade in NC Machining Based on BP Neural Network and Genetic Algorithm[J]. Applied Mechanics and Materials, 2014, 496/497/498/499/500: 1539-1542

[9] 黄天然,史耀耀,辛红敏. 基于盘铣加工钛合金表面残余应力的工艺参数优化[J]. 计算机集成制造系统,2015,21(9):2403-2409

Huang Tianran, Shi Yaoyao, Xin Hongmin. Parameters Optimization on Surface Residual Stress for Titanium Alloy Based on Disk Milling Process[J]. Computer Integrated Manufacturing System, 2015, 21(9): 2403-2409 (in Chinese)

[10] 孙玉文. 自动抛光技术及其工艺参数优化研究[D]. 大连: 大连理工大学, 2015

Sun Yuwen. Automatic Polishing Technique and Parameter Optimization[D]. Dalian, Dalian University of Technology, 2015 (in Chinese)

[11] Kumar S V, Kumar M P. Optimization of Cryogenic Cooled EDM Process Parameters Using Relational Analysis[J]. Journal of Mechanical Science and Technology, 2014, 28(9): 3777-3784

[12] Palanisamy A, Rekha R, Sivasankaran S, et al. Multi-Objective Optimization of EDM Parameters Using Grey Relational Analysis for Titanium Alloy(Ti-6Al-4V)[J]. Applied Mechanics and Materials,2014, 592/593/594: 540-544

[13] Manikandan N, Kumanan S, Sathiyanarayanan C. Multi Response Optimization of Eletrochemical Drilling of Titanium Alloy(Ti-6Al-4V) Using Taguchi Based Grey Relational Analysis[J]. Indian Journal of Engineering and Materials Sciences, 2015,22(2): 153-160

[14] Vaxevanidis N M, Fountas N A, Kechagias J D, et al. Optimization of Main Cutting Force and Surface Roughness in Turning of Ti-6Al-4V Titanium Alloy Using Design of Experiment and Artificial Neural Networks[C]∥International Conference on Engineering and Applied Sciences Optimization, 2014,1:2889-2906

[15] Nandakumar C, Mohan B. Multi-Response Optimization of CNC WEDM Process Parameters for Machining Titanium Alloy Ti-6Al-4V Using Response Surface Method0Logy(RSM)[J]. Applied Mechanics and Materials, 2014,541/542: 354-358

[16] Gunay M. Optimization with Taguchi Method of Cutting Parameters and Tool Noise Radius in Machining of AISI 316I Steel[J]. Journal of the Faculty of Engineering and Architecture of Gazi University, 2013, 28(3): 437-444

[17] Lai X Y, Yan C Y, Zhan C Y, et al. Machining Parameters Optimization on Micro Hole Vibration Drilling Using Grey System Theory[C]∥2015 IEEE International Conference on Mechatronics and Automation, 2015: 2307-2312

[18] Xu J, Wang C X. Study on Application of Grey System Theory in Fatigue Span Design of Machine Tool Axles[J]. Advanced Materials Research, 2011, 201/202/203: 1156-1160

[19] 肖新平, 宋中民, 李峰.灰技术基础及其应用[M]. 北京: 科学出版社,2005

Xiao Xinping, Song Zhongmin, Li Feng. Grey Technology Fundamental and Application[M]. Beijing, Science Press, 2005 (in Chinese)

[20] 孙玉刚. 灰色关联分析及其应用的研究[D]. 南京: 南京航空航天大学, 2007

Sun Yugang. Research on Grey Incidence Analysis and its Application[D]. Nanjing, Nanjing University of Aeronautics and Astronautics, 2007 (in Chinese)