混沌多步控制在地月轨道转移中的应用

郑越, 泮斌峰, 唐硕, 王洋

(1.西北工业大学 航天学院, 陕西 西安 710072; 2.陕西省空天飞行器设计重点实验室, 陕西 西安 710072)

低能耗是地月轨道转移中需要考虑的重要问题。航天器在地月三体系统的混沌区域可以不耗费任何能量到达月球附近,但同时也导致地月轨道转移耗时过长。因此,在利用混沌运动低能量特性的同时,如何有效减少轨道转移时间是实现大规模、低成本探月活动的迫切需求,对我国探月工程的发展具有非常重要的意义。

目前采用混沌控制理论设计轨道的研究尚处于起步阶段。Bollt等[1]通过搜索得到轨道在庞加莱截面图上投影距离小于预定约束值的2个点,将2点之间的轨迹从轨道中截断,并根据截断点的稳定方向和不稳定方向,拼接出转移轨道。Salazar等[2]增大了约束值,缩短了转移时间,代价是转移过程中需要非常大的能量。Macau[3]搜索分别从地球和月球附近出发的轨道,通过找出一组在庞加莱截面图上投影距离非常接近的投影点,利用Bollt拼接稳定方向与不稳定方向的方法完成地月轨道转移。Schroer等[4]将不稳定周期轨道与向前-向后法相结合,实现地月轨道转移。

为了减小地月转移过程中所需要的能量,现有的混沌控制方法[1-4]都利用了轨道在庞加莱截面图上的投影点的稳定方向与不稳定方向的交点,通过迭代减小实现轨道拼接所需要的能量。不足之处是这些方法都要求在庞加莱截面图中存在轨道投影位置非常接近的点,然而采用同一轨道截断[1-2]方法或不同轨道拼接[3-4]都不易满足上述要求。对于同一轨道截断的方法,需要轨道本身存在位置接近的投影点;而对于不同轨道拼接的方法,则需要在随机搜索的基础上找到投影点位置接近的点。此外,这种依靠投影点的稳定方向与不稳定方向交点的方法在两投影点距离不足够小的情况下成功率很低[5]。尽管利用周期轨道作为中间轨道[4]可以提高算法的成功率,但是需要完全依赖于周期轨道来实现地月轨道转移。

针对现有混沌控制方法存在的依赖随机搜索、周期轨道实现地月轨道转移、成功率低等缺点,本文提出一种混沌多步控制方法来实现低能地月轨道转移。该方法在总结地月快速转移规律的基础上,采用多步控制方法以尽可能减少航天器在混沌区域滑行时间,同时利用自适应粒子群优化算法计算出每次对轨道进行控制时所需要的扰动。仿真结果表明,本文提出的方法在节省转移时间的前提下,能够有效地实现低能地月轨道转移。

1 圆形限制性三体系统

1.1 动力学模型

航天器在地月系统中的飞行轨迹通常在圆型限制性三体问题(circular restricted three-body problem,CRTBP)动力学模型中模拟,CRTBP描述了质量可以忽略的航天器在地球和月球2个主天体的引力作用下的运动,其中主天体绕其公共质心做匀速圆周运动[6-8]。归一化地球质量m1和月球质量m2之和为单位质量,则:

(1)

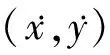
(2)

式中,Ω为旋转坐标系下的等效势能:

(3)

设矢量r1,r2为航天器到2个主天体的距离,有:

(4)

CRTBP系统中,存在雅可比积分如下:

(5)

在地月三体系统中,单位长度为地月之间的距离,L=3.844×105km,单位时间为T=104 h,单位速度为V=1 024 m/s。

1.2 常用坐标系的转换

地月三体系统中常用的坐标系有地月质心旋转坐标系、地月质心惯性坐标系和地心惯性坐标系。图1描述了常用坐标系之间的关系,图1a)为地月质心惯性坐标系(下标为I)与地月质心旋转坐标系(下标为R)之间的关系,θ为惯性坐标系与旋转坐标系的夹角;图1b)为地月质心惯性坐标系(下标为I)与地心惯性坐标系(下标为EI)之间的关系。

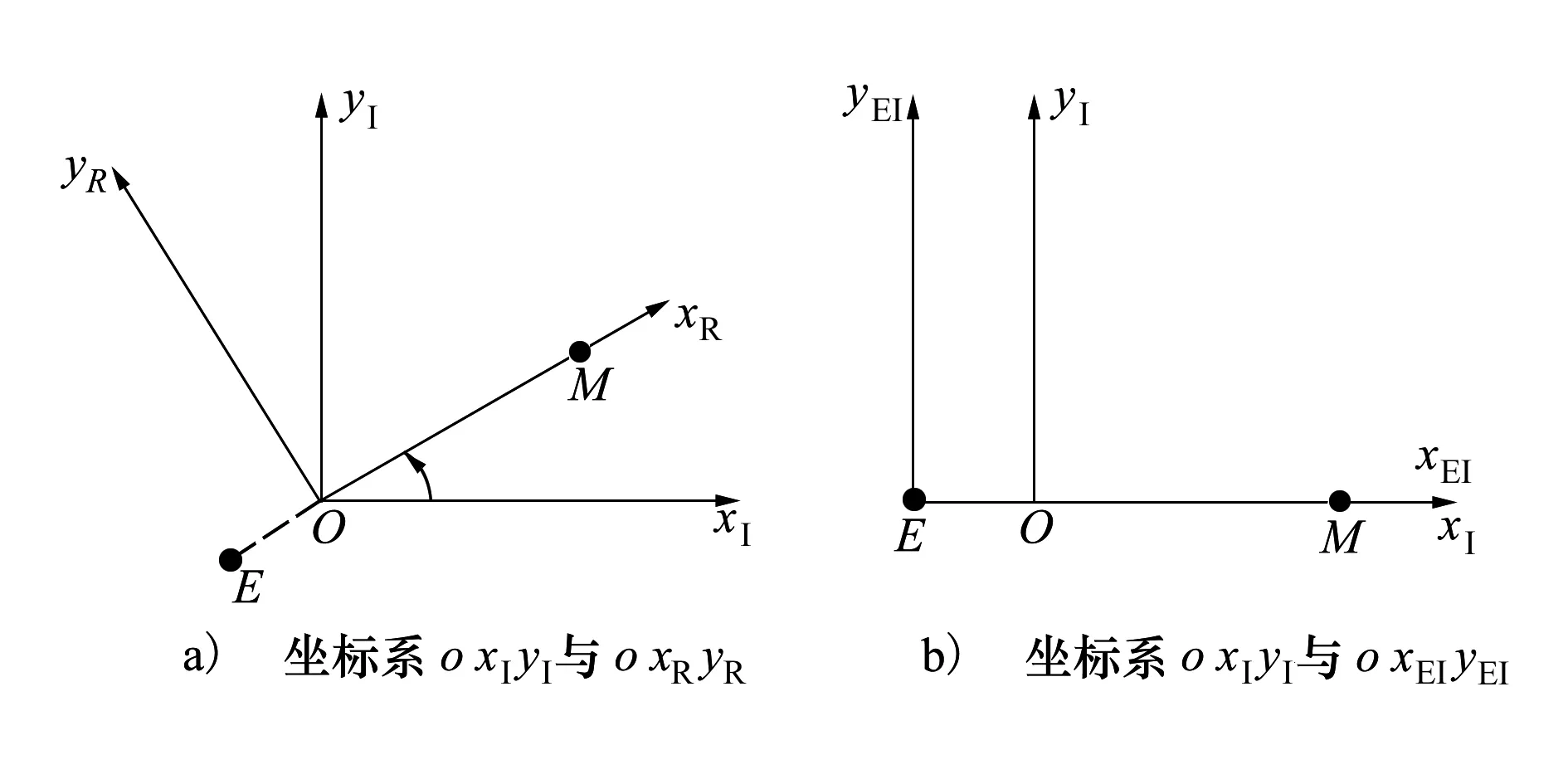
图1 坐标系的转换

从地月质心旋转坐标系到地月质心惯性坐标系的转换关系为[9]:

(6)

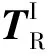
(7)

(8)

(9)

所以从地月质心旋转坐标系到地心惯性坐标系的转换关系为:

(10)

2 地月低能轨道转移方法

航天器在三体系统下常常呈现混沌运动状态,使航天器能够在不耗能的情况下仅仅通过弹道捕获至月球附近,但航天器在混沌区域的滑行时间也往往过长。由于混沌系统具有内在敏感性[10-12],表现为对系统施加小的扰动,会使系统偏离固有轨迹而运动。而混沌运动本身具有的内在随机性和长期趋势不可预见性增加了对其进行控制的难度,所以何时以及如何施加扰动,尽可能减少航天器在混沌区域的飞行时间是实现低能地月轨道转移需要解决的问题。

本文通过航天器轨迹在地月质心旋转坐标系和地心惯性坐标系的对比分析,找出通过月球的弹道捕获[13-14]减少航天器在混沌区域滑行时间的规律;根据这个规律将航天器每次与月球接近的点作为控制点,设计出一种通过多步控制来实现的地月低能轨道转移方法;最后利用自适应粒子群优化算法计算每一步控制所需要的扰动。

2.1 轨迹分析

航天器能够在不耗能的情况下仅仅通过弹道捕获到达月球附近。航天器在地月三体系统下不耗费任何能量的滑行过程可以认为是在地球和月球共同作用下的结果,地月轨道转移则是航天器每次靠近月球时通过月球的弹道捕获最终滑行至月球附近的过程,而如何有效利用月球的弹道捕获是实现低能地月轨道转移首先要考虑的问题。

地月低能转移是航天器从近地周期轨道出发飞行至近月周期轨道的过程。为了减少转移中所消耗的能量,一般选择雅可比能量略大于CL1=3.188 3的能量。图2为雅可比能量C=3.179 48下的庞加莱截面图[15],庞加莱截面图中存在由环状结构组成的KAM环区域和由杂乱点组成的混沌区域。平动点L1[16]将地月系统分为地球引力区和月球引力区,航天器在混沌区域能够不消耗任何能量从地球引力区通过平动点L1滑行至月球引力区进而到达月球附近,但同时导致航天器在地球引力区的混沌区域滑行时间过长。航天器在地月系统的地球引力区的滑行过程是一个在动力作用下远离地球,而在地球引力作用下速度逐渐变小而再向地球附近滑行的一个往复过程。分别定义初始点在地月连线上(离地球 距 离 递 增, 分 别 为 0.135 106 485 040 224,

0.161 974 247 434 113,0.184 885 116 403 981),初始速度垂直上穿横轴的一组轨道为轨道a、轨道b、轨道c。如图3所示,图3a)～图3c)分别为轨道a、轨道b、轨道c在地月质心旋转坐标系和地心惯性坐标系下的对比图。可以看出,随着轨道初始位置从地球附近向月球方向靠近,航天器一个往复过程的轨迹在地月质心旋转坐标系和地心惯性坐标系下的形状也随之改变。可以发现,航天器远离和靠近地球的一个往复过程在惯性坐标系下的运行轨迹近似于一个椭圆。图3d)为轨道a、轨道b、轨道c在地心惯性坐标系的轨迹对比,当航天器近地点离地球较近时,其椭圆轨迹具有较大的偏心率,当航天器轨迹近地点离地球较远时,其椭圆轨迹具有较小的偏心率,而随着椭圆轨迹偏心率增大到一定程度,航天器可以克服地球引力穿过L1瓶颈区域受月球引力作用而到达月球附近。

基于分析可知,航天器在地月系统滑行的过程中, 每次接近月球时受到月球的影响最大,可以改变其运行轨迹。当航天器所受到的影响使其飞行轨迹的近地距离减小时,会造成飞行时间的增加,而当航天器所受到的影响使其飞行轨迹的近地距离增大时,航天器可能在下一次脱离地球引力而滑行至月球附近。

图2 地月系统庞加莱截面图

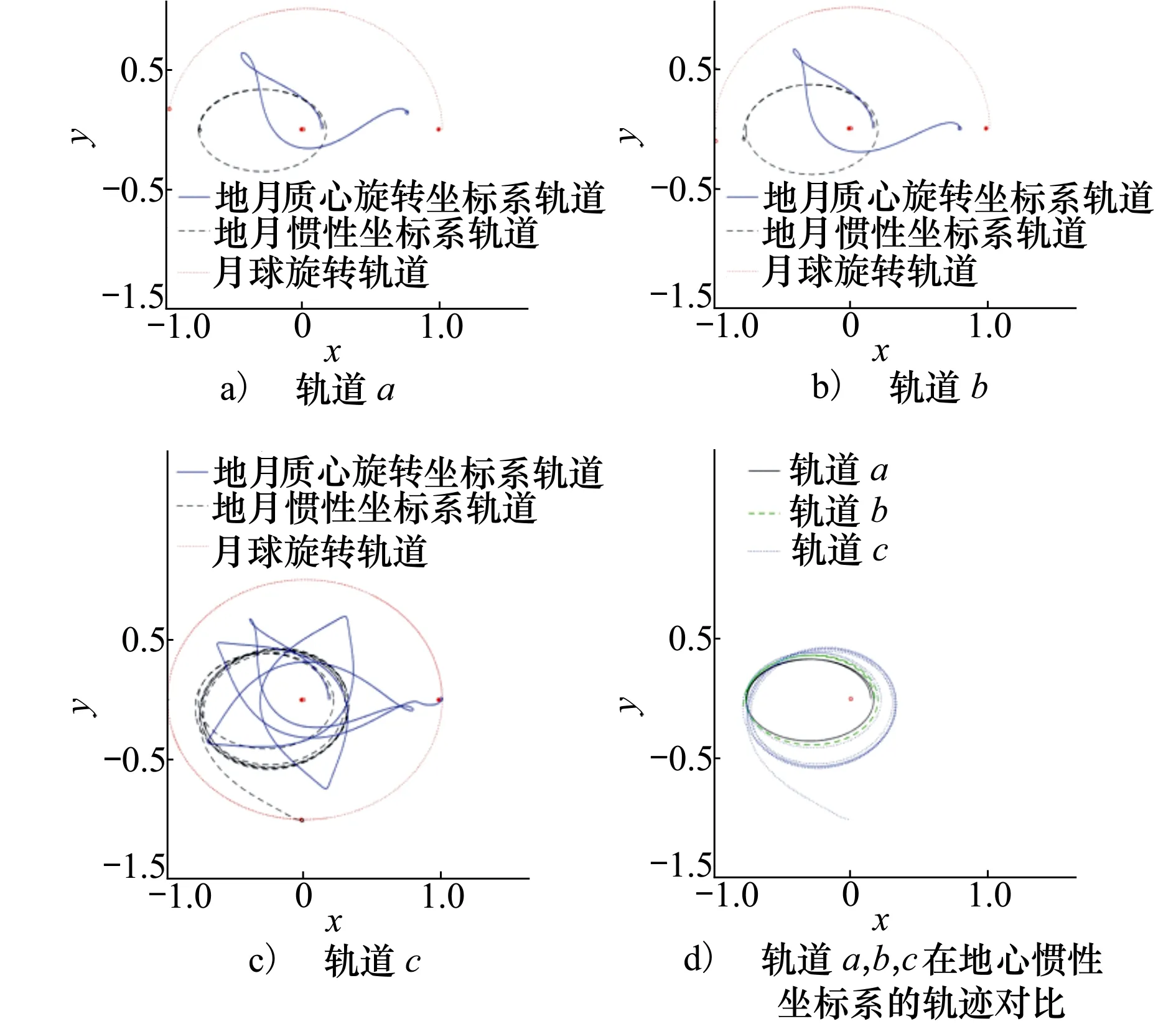
图3 航天器位于不同初始值的轨道

2.2 算法流程

在对地月系统下航天器轨迹的分析的基础上,本文设计了一种低能轨道转移方法,其算法流程如图4所示。

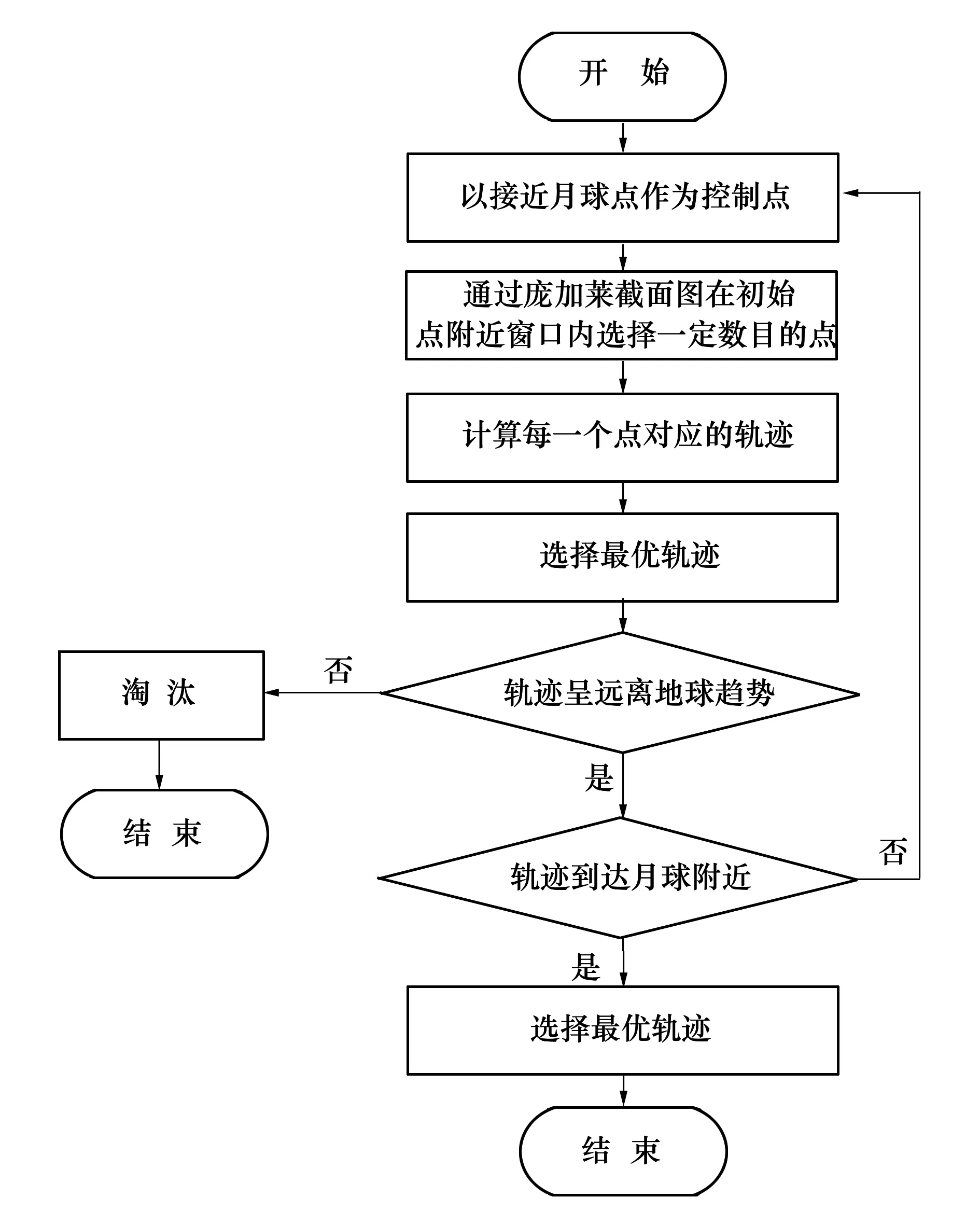
图4 地月轨道转移方法

该方法通过多步控制,对每次航天器接近月球时的控制点施加速度方向的小扰动。扰动的大小选择在预设最大扰动范围内,能够在施加控制后使轨迹最优的速度增量。判断最优轨迹的标准是当航天器下一次与月球接近时如果能到达月球附近,则选择在庞加莱截面图上最靠近月球附近的KAM环的轨迹作为最优轨迹;当航天器下一次与月球接近时如果不能到达月球附近,则选择近地点离地球最远的轨迹作为最优轨迹。本文方法通过对航天器在混沌区域的轨道实施多次控制找出每次的最优扰动量,直到轨迹可以运行至月球附近。而航天器轨迹近地距离的增大可以使其在混沌区域的滑行时间减少,所以为了尽量减少地月低能转移时间,本方法要求航天器到达月球附近前每次与月球接近时的近地点呈递增趋势。

2.3 扰动计算

通过每次航天器运行轨道与月球转动位置非常接近时,施加小的扰动可以使轨道运行状态发生很大改变已达到减少航天器在混沌区域的滑行时间而尽快飞行至月球附近的目的,而扰动的大小可以由自适应粒子群优化算法(adaptive particle swarm optimization,APSO)计算得到。

粒子群优化算法(particle swarm optimization,PSO)是一种通过观察鸟类觅食行为启发而得到的进化算法[17-18]。PSO算法保留了基于种群的全局搜索策略,只是采用简单的速度位移模式,通过对个体最优和全局最优的记忆使其可以动态追踪当前的搜索情况以调整其搜索策略,具有较强的全局收敛能力和鲁棒性。APSO算法通过对惯性权值的自适应调整,能够保证粒子具有很好的全局搜索能力和较快的收敛速度。

APSO算法的流程如图5所示。

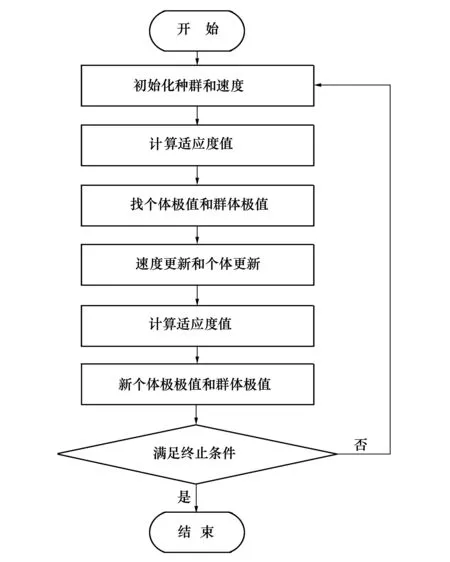
图5 自适应粒子群优化算法

设在一个S维的目标搜索空间中,有m个粒子组成一个群体,每个粒子表示为一个n维的向量,APSO算法的2个主要操作是速度和位移方程,在粒子寻优过程中,第i个粒子第s维向量的运动轨迹描述如下:

(11)

式中,c1和c2为学习因子,是非负常数,r1s和r2s服从[0,1]上的均匀分布的随机数,vis是粒子的速度,vis∈[vmin,vmax],vmin和vmax分别表示粒子速度的下限和上限。pis为局部最优位置,是第i个粒子迄今为止搜索到的最优位置,pgs为全局最优位置,ω是惯性权值,满足:

(12)

式中，f为粒子的适应度值,由每个粒子的位置决定,根据适应度值的大小衡量解的优劣。favg为平均适应度值,fmin为最优适应度值(最优适应度值的选择根据具体问题调整)。最后通过每个粒子的适应度值调整局部和全局最优位置直到满足终止条件。

APSO算法的终止条件根据具体问题取最大迭代次数或粒子群搜索到的最优位置满足的预定最小适应阈值。本文方法利用最大迭代次数,在轨道未到达月球附近时,选择导致轨道近地点离地球最远的扰动为最佳扰动,而当轨道可以到达月球附近时,选择能够使轨道到达离与月球附近拟周期轨道最近的扰动作为最优扰动。

3 数值验证

地月轨道转移就是对地球附近的周期轨道上的航天器施加冲量,使其飞行至月球附近,然后再对其施加冲量使其绕月飞行。在地月三体系统中,选择图2中距离地心59 669 km的围绕着地球旋转的周期轨道上的点P作为地月转移轨道的初始点,在雅可比能量C=7.172 18时航天器通过P点围绕着地球做周期运动(由于参数精度选择有差异,本文所得到的周期轨道雅可比能量与文献[1-4]中的C=7.173 8不一致),施加一个平行的推力使航天器进入混沌区域。此时系统雅可比能量为C=3.179 48,这要求速度的改变ΔVP=748 m/s(文献[1-4]中ΔVP=744.4 m/s)。如图3所示,点P包围在混沌区域内,当轨道转移到月球附近并距离月球附近的KAM环很近时,便可以通过一个很小的推力使轨道流形进入KAM环的边缘而绕月运动。

当系统雅可比能量C=3.179 48,航天器在不施加外力的情况下从庞加莱截面图上的P点滑行到月球附近需约27年的时间。在数年的滑行过程中,航天器并未长时间停留在月球附近,而是在月球附近飞行数圈后便很快远离。图6为航天器在系统雅可比能量C=3.179 48下从P点自由滑行的轨迹。

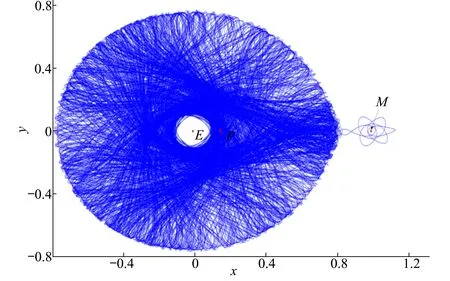
图6 P点出发到月球附近的轨道流形

根据图2的庞加莱截面图,本文计算了在不同扰动值下,从P点出发飞行至离月球附近KAM环极近、距离月心13 970 km的T点的地月转移轨迹。设置APSO算法中的学习因子c1=c2=2, 惯性权值ωmax=0.9,ωmin=0.6。设置控制轨迹能够到达距离T点的精度为0.01,则通过4 m/s的速度增量便可以使轨道流形进入KAM环的边缘而绕月运动。图7为本文方法所完成的地月轨道转移,图7a)～d)对控制点施加速度方向的扰动量的最大值分别设置为0.006 3,0.07,0.16,0.2。表1分别列出轨道转移所需的扰动次数、转移时间、以及轨道转移过程中所需要的总的速度增量。

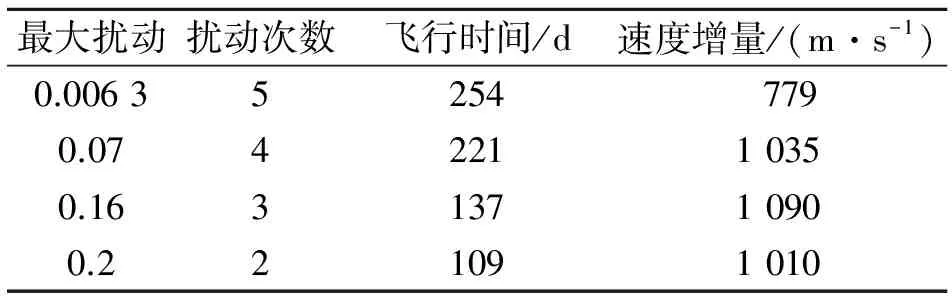
表1 地月轨道转移的需用扰动、速度增量和飞行时间

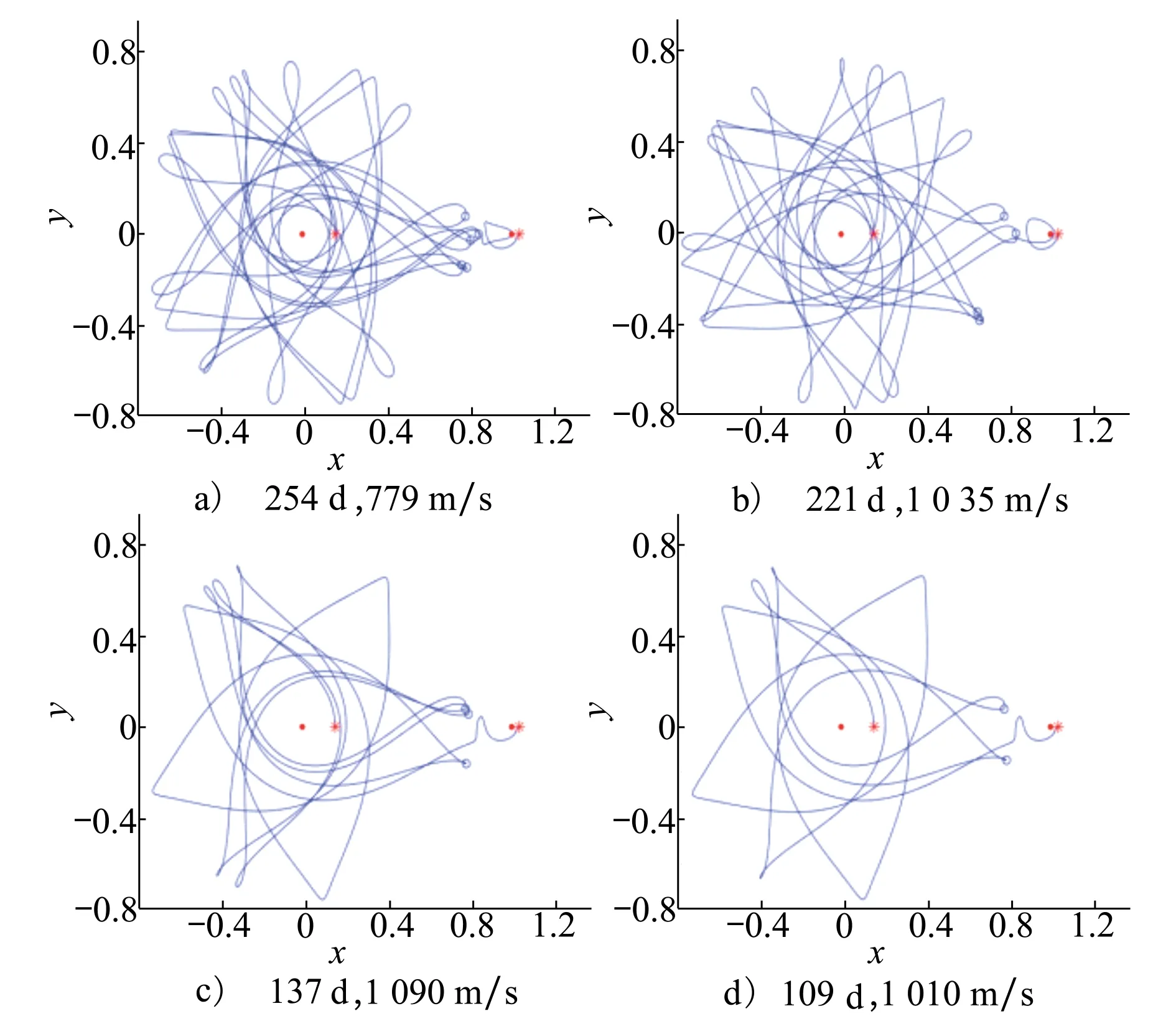
图7 地月转移轨道

由仿真结果可见,扰动窗口较大时,地月轨道转移所需要的扰动次数相对较少,转移时间较短;而扰动窗口较小时,地月轨道转移所需要的扰动次数相对较多,转移时间也较长。文献[1-4]中,所需要的转移时间最短为284 d,所需要的速度增量为ΔV=767.8 m/s(见文献[3]),本文所得到的转移轨道均比284 d短,其中,图7a)所需要的速度增量仅略大于文献[3]在转移过程中所需要的速度增量,在耗能较小的前提下显著缩短了地月轨道转移时间。

4 结 论

本文通过对航天器在地月三体模型下轨迹运行规律的分析,利用APSO算法计算航天器每次接近月球时的扰动,通过多步控制,在有效减少航天器在混沌区域游荡时间的基础上完成地月低能轨道转移。该方法避免了随机大量的搜索,也不需要依靠周期轨道等中间轨道,能够在保证用时短,耗能小的前提下得出地月转移轨道。本文方法是通过对每次航天器与月球接近时施加扰动,通过在预先设定的扰动范围内找出每次施加扰动后的局部最优轨迹,进而在尽可能节省时间的前提下完成地月低能轨道转移。下一步的工作是如何在综合用时短和耗能小的前提下确定全局最优转移轨道的标准,并通过相应的扰动值完成最优地月轨道转移。

[1] Bollt E M, Meiss J D. Targeting Chaotic Orbits to the Moon through Recurrence[J]. Physics Letters A, 1995, 204(5/6):373-378

[2] Salazar F J T, Macau E E N, Winter O C. Chaoic Dynamics in a Low-Energy Transfer Strategy to the Equilateral Equilibrium Points in the Earth-Moon System[J]. International Journal of Bifurcation & Chaos, 2015, 25(5):1550077

[3] Macau E E N. Using Chaos to Guide a Spacecraft to the Moon[J]. Acta Astronautica, 2000, 47(12): 871-878

[4] Schroer C G, Ott E. Targeting in Hamiltonian Systems That Have Mixed Regular/Chaotic Phase Spaces[J]. Chaos, 1997, 7(4):512-519

[5] Bollt E M, Meiss J D. Controlling Chaotic Transport through Recurrence[J]. Physica D Nonlinear Phenomena, 1995, 81(3):280-294

[6] Szebehely V, Jefferys W H. Theory of Orbits: the Restricted Problem of Three Bodies[J]. American Journal of Physics, 1968, 36(4):375-375

[7] Koon W S, Lo M W, Marsden J E, et al. Dynamical Systems, the Three-Body Problem and Space Mission Design[M]. New York, Springer-Verlag, 2007

[8] 刘林. 航天器轨道理论[M]. 国防工业出版社, 2000

Liu Li. Orbit Theory of Spacecraft[M]. Beijing, National Defence Industry Press, 2000: 452-462 (in Chinese)

[9] 张文博. 循环飞行方案的轨道设计与优化[D]. 北京理工大学, 2015. 26-28

Zhang Wenbo. Trajectory Design and Optimization for Cycler Architecture[D]. Beijing, Beijing Institute of Technology, 2015: 26-28

[10] 胡岗,萧井华,郑志刚. 混沌控制[M].上海:上海科技教育出版社, 2000: 24-27

Hu Gang, Xiao Jinhua, Zheng Zhigang. Chaos Control[M]. Shanghai, Shanghai Science and Technology Education Publishing House, 2000: 24-27 (in Chinese)

[11] Strogatz Steven H. Nonlinear Dynamics and Chaos: with Applications to Physics, Biology, Chemistry, and Engineering[M]. Perseus Books Publishing, 2000: 285-455

[12] Lai Y C, Tél T. Transient Chaos: Complex Dynamics on Finite-Time Scales[M]. USA, Springer, 2011: 187-237

[13] Hyeraci N, Topputo F. A Method to Design Ballistic Capture in the Elliptic Restricted Three-Body Problem[J]. Journal of Guidance Control & Dynamics, 2010, 33(6):1814-1823

[14] Belbruno E, Topputo F, Gidea M. Resonance Transitions Associated to Weak Capture in the Restricted Three-Body Problem[J]. Advances in Space Research, 2008, 42(8):1330-1351

[15] Jung C. Poincare Map for Scattering States[J]. Journal of Physics a General Physics, 1998, 19(8):1345-1353

[16] 孟云鹤,张跃东,陈琪锋. 平动点航天器动力学与控制[M]. 北京：科学出版社, 2014: 24-27

Meng Yunhe, Zhang Yuedong, Chen Qifen. Dynamics and Control of Spacecraft near Libration Points[M]. Beijing, Science Press, 2014: 24-27 (in Chinese)

[17] Kennedy J, Eberhart R. Particle Swarm Optimization[C]∥IEEE International Conference on Neural Networks, 1995

[18] 方群, 徐青. 基于改进粒子群算法的无人机三维航迹规划[J]. 西北工业大学学报, 2017, 35(1):66-73

Fang Qun, Xu Qin. 3D Route Planning for UAV Based on Improved PSO Algorithm[J]. Journal of Northwestern Polytechnical University, 2017, 35(1):66-73 (in Chinese)