基于蚁群算法的项目型制造企业定价方法研究

徐静

(大连理工大学管理与经济学部，辽宁 大连 116024)

0 引言

项目型制造企业为国民经济各部门的生产提供了根本保证[1]。随着市场竞争的加剧及客户定制化服务的普及，项目型制造企业面临着前所未有的挑战。客户需求波动增大、质量要求较高、对交货期和价格更为敏感，这些在很大程度上增加了项目型制造企业定价的难度。而项目管理方法即是在有限的时间和成本内，设计生产产品以满足客户需求[2]。在以客户个性化为主导的今天，如何有效地组织企业生产资源、制定合理的定价方法，满足客户的交货期和质量要求并保证企业的盈利水平，成为每个项目型制造企业面临的重要问题。

在需求不确定的定价方法研究方面：Granot[3]在乘法式、加和式需求假设下，对比分析了报童模型的定价和订购延迟问题。Mardaneh[4]在生产能力受限约束下假设需求依赖于价格，建立两阶段优化定价模型，采用半随机算法求解最优价格及产量。Chaharsooghi[5]在随机需求、产能受限条件下建立两阶段随机规划定价模型，分析了价格、提前期及交付期柔性对价格和提前期决策的影响。Palaka等[6]在M/M/1服务系统中假设需求是价格和提前期的线性函数且对提前期敏感，研究不同敏感客户的交货期设置、产能利用和定价决策。Deng等[7]针对离散时间框架下的生产和定价协同决策问题，分析了不同产能、库存和生产准备成本组合下的最优解。上述定价方法主要考虑需求和生产能力约束，忽略了对质量问题的研究。

在联合定价方面：Zhang等[8]在MTO环境中以期望利润最大为目标，重点分析了客户不同偏好信息对目标值的影响；戴道明等[9]研究了允许需求延迟情形下产品的动态定价和订货批量的联合决策问题。柏庆国等[10]通过分析最优解的相关性质，设计算法求解联合库存与定价策略问题，并以实例验证了相关参数变化对联合策略的影响。Li等[11]设计多阶段算法求解允许延迟交货的联合批量和定价模型，但只考虑了单一产品的问题。Heuvel[12]针对需求是价格的确定性函数且产能不限的经济批量模型，设计多项式时间算法协同优化定价和库存决策，但假设不同阶段价格相同，使得模型过于简单。

上述文献侧重于研究联合决策的定价方法，但未考虑生产能力；在研究联合定价决策时多考虑需求因素、批量及库存等问题，对客户所关心的质量问题鲜有研究。针对上述问题，本文以项目型制造企业为研究对象，考虑客户对产品交货期和质量的要求，以需求随机、生产能力受限为约束，产品总利润最大、平均质量最高为目标，建立多产品动态定价模型。并设计蚂蚁的寻优启发式规则，使双目标问题达到帕累托(Pareto)最优。

1 问题描述

本文考虑某项目型制造企业在单台机器上加工多种产品的情形。生产共需n(i=1,2,…,n)种原材料，产品序列为p=1,2,…,j,…,J， 以利润最大、平均质量最高为目标，考虑需求和生产能力约束的多产品动态定价问题可描述为：

(1)在任一周期t(t=1,2,…,T)， 企业在期初为第j种产品设置价格、承诺交货期区间[5]。

(2)企业根据新订单的产品价格、承诺交货期以及产品质量确定订货量，再根据订单需求设计和生产，产品j在各阶段的生产量不大于需求量。

(3)任一周期企业内部的生产能力是固定的，但可通过工人加班、业务外包等措施扩大生产能力。

(4)开始或切换产品生产前需要一定的准备时间，且准备时间与产品序列有关，故考虑生产准备成本。

(5)客户不接受提前交货且对延迟敏感。

(6)任一周期任一产品的需求与其他周期无关。

为更深入地研究此类问题，本文做出以下假设：

(1)所有产品初始库存为0。

(2)需求是价格、承诺交货期和产品质量的函数[13]。

(3)若订单在承诺交货期之前完成生产，则产生库存持有成本；若在承诺交货期之后、周期t期末交货，则产生拖期成本[5]。

(4)某周期生产时间截止时，若有未满足需求，则发生缺货成本[14]。

(5)在产品初始投入一定时，假设此项目型制造企业能够提供的产品质量m与承诺交货期线性相关[6]；另外，受生产能力的限制，企业提供的产品质量存在上限。

2 多产品动态定价模型

2.1 变量定义

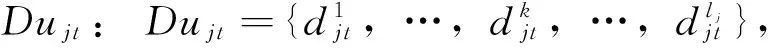
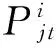
cjt： 产品j在t阶段的单位生产成本；

ajt： 产品j在t阶段的生产准备成本，与产品排序有关；

hjt，rjt： 产品j在t周期内的单位时间持有成本、单位拖期成本，rjt≥hjt[15]；

Ijt： 产品j在t周期的库存持有时间；

wj： 产品j的缺货惩罚因子；

Kt： 周期t内企业的生产能力；

vj： 生产单位j消耗的生产能力；

Uj： 产品j的总生产量；

Yjt： 二元变量，可取值为0，1；

mjt： 周期t内产品j的质量水平。

2.2 模型设计

为使项目型制造企业获得最优价格，考虑客户对交货期和质量的要求，以需求、生产能力为约束，以利润最大、产品平均质量最高为目标，构建数学模型如下。

2.2.1 目标函数

(1)企业总利润最大。式(1)中的各项依次表示收入、生产成本、生产准备成本、库存持有成本、拖期成本和缺货成本。最后一项表示所有周期内、所有产品的缺货量乘以对应的缺货惩罚因子之和，即为总缺货成本

(1)

(2)平均质量最高。以所有产品的质量之和除以总产品数计算。即

(2)

2.2.2 约束条件

(1)生产量约束。任一周期t内产品j的生产量不大于需求量。即

∀j∈J；i=1,2,…,nj

(2)生产能力约束。某一周期t内生产所有产品消耗的产能不大于同周期的生产能力Kt。 即

∀j,∀t

(3)持有成本和拖期成本约束。在任一周期内不同时出现持有成本和拖期成本。即

IjtVjkt=0 ∀j,∀t

(4)总生产量约束。产品j总生产量的计算公式。即

∀j

(5)质量影响因子约束。交货期对质量的影响因子具有一定的范围限制，δmax,δmin分别表示其上下限。即

δmin≤δ≤δmax

(6)生产准备约束。产品j一旦被生产，则产生生产准备成本。即

∀j,∀t

(7)变量非负约束。价格、产量、持有时间、延迟交货时间为非负值。即

此双目标问题是混合整数非线性组合优化问题，且含有随机变量，解的规模较大；另外，当项目型制造企业追逐利润最大时往往不能兼顾质量，质量最优时企业不一定获得最大利润，因此两目标之间存在悖反关系，本文采用基于非支配排序的混合蚁群算法来获取非劣解。

3 算法设计

蚁群算法在求解组合优化问题上表现出良好的性能[16]。根据项目型制造企业客户需求难以预测的特点，对需求函数的随机变量进行情景描述，并设计基于各目标的蚂蚁寻优启发式规则，使蚂蚁能够找到非劣解。

3.1 随机变量的情景设计

需求函数中的随机变量ξj用于描述客户需求的不确定性。采用情景树[14]的思想设计了随机变量的处理方法，具体步骤如下(以下情景设计只针对单个产品，多产品分别进行设计即可)：

步骤1：假设ξj服从期望为E、 方差为D的指数分布[15]，根据产品种数、周期及统计指标i(如期望、方差等)设置随机变量的情景个数。

步骤2：记录随机变量不同情景下的值xi及其生成概率pi， 按照式(3)计算目标值fi(x,p)为

(3)

∑pi=1pi≥0

(4)

式(3)是求统计值与标准值之间误差最小，式(4)保证所有情景的概率之和为1。目标值越趋近于0，表明不同情境下的数据对随机变量的趋近效果越好。

步骤3：重复n次步骤2，逐次记录按式(3)计算出的最优目标值及其对应的随机变量的情景值及其概率。

步骤4：计算步骤3中不同情景之间的欧氏距离，并乘以对应的条件概率(每个周期的pi相乘)，得到不同情景的权重距离weight_distance。

步骤5：记录所有的权重距离，其中最小的权重距离对应的情景scenario即为随机变量的最优取值。

3.2 蚁群参数设计

3.2.1 启发式信息计算

针对不同目标yi(i=1,2)分别设计启发式信息：

3.2.2 信息素更新规则

为获得Optimal最优解，分别针对各目标对信息素进行全局更新。计算公式如下

式中，φ是信息素挥发系数，φ∈(0,1)；PNC是第NC次迭代中允许更新信息素的蚂蚁集合；Δτa(NC)表示蚂蚁a在第NC次迭代中对应于目标yi的信息素增量；Qi表示针对目标值f(yi)设定的调整系数，即

Δτa=Qi/f(yi)

3.3 算法步骤

步骤1：初始化矩阵、参数设置，蚂蚁数为m，最大运行时间t0。

步骤2：建立非劣解集fzp， 设置t=0， 将蚂蚁均分至各子空间。

步骤3：按照3.1中的策略，对需求函数中的随机变量ξj进行模拟计算。

步骤4：将蚂蚁随机放在各变量节点之上并进行寻优。

步骤5：计算在第yi(i=1,2)个目标下，选择下一变量节点的转移概率Ps0s， 设置阈值q0，q0∈(0,1)， 若随机数q>q0， 则蚂蚁选择转移概率中最大的节点转移；若q≤q0，则蚂蚁按照轮盘赌的方式选择下一个节点。

步骤6：根据式(1)、式(2)计算目标值。

步骤7：根据本次迭代计算非劣解，更新fzp集合，并保留fzp集合中解的路径。

步骤8：为fzp集合中每条解的路径进行信息素的全局更新。

步骤9：NC=NC+1， 记录运行时间t， 若t=t0则转至步骤10，否则转至步骤3。

步骤10：输出fzp解集。

4 实例应用

4.1 算法结果分析

采用文献[15]中测试算例的生成规则，考虑产品数量、生产能力、交货期的影响。产品数量分为四类(J1类:20，J2类:50，J3类:100，J4类：150)；产品交货期(J1类：服从[5,20]离散均匀分布，J2类：服从[15,30]离散均匀分布，J3类：服从[30,45]离散均匀分布，J4类：服从[45,60]离散均匀分布)，生产能力分两类(C1: 低生产能力，C2： 高生产能力)。生产时间随机生成，产品价格从有界整数集P(j)={pj:10≤pj≤60}上选取，hjt=0.5，rjt=1，T=3。

设置最大运行时间t0=60s， 信息素权重α=0.01， 启发式信息权重β=0.2， 信息素挥发系数φ=0.2， 蚂蚁数m=20， 调整系数：Q1=1000,Q2=0.01，θ=1。 在PC机(Intel(R)Core(TM)i7-3770CPU@3.40GHz，8.00GB)上使用Matlab软件对8组算例各运行10次，各目标的极大值见表1。

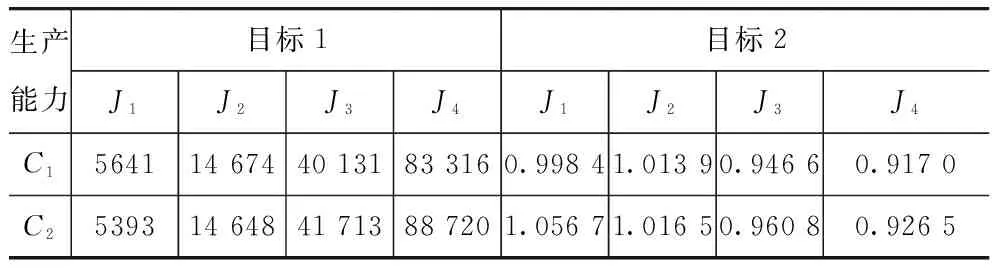
表1 各目标极值

如表1所示，根据统计结果可知，随着产品数量的增加，混合算法对利润目标的优化程度呈现“∧”型特征，对质量目标的优化程度呈现“∨”型特征，表明该算法在中等规模问题上优化效果更好；在高生产能力水平下，各算例下的质量目标都有所提升，大规模算例下利润目标有所增加而小规模算例下利润目标降低，说明扩大生产能力并不一定会给企业带来更高的利润，但会在一定程度上提高质量。为了进一步探究在不同交货期条件下价格和利润目标随生产能力的变化而变化的趋势，进行数值实验见图1(以J1算例为例)。

由图1可知，在不同交货期影响下，产能的增加导致产品价格的降低，从而吸引了更多的客户、消耗更多的产能，企业利润逐渐增加，这与文献[17]的结论相同。在一定范围内，产能增加使得企业能够按时交货，质量上升；而超出这个范围后，质量目标受交货期影响的程度大于产能，交货期越短，质量目标的满足率就越低。具体来看，当交货期为10和11时，价格随产能增加而下降的速率为先减后增，而利润上升的速度先增后减，这是由价格下降带来的收益与增加产能消耗的成本不平衡产生的结果，而质量由于受到交货期和产能的双重影响，变化趋势为先增后减；当交货期为8时，客户对交货期的要求较高，企业必须调动一切生产资源保证交货，因此价格下降的速度缓慢、质量变化幅度较大。而利润上升的趋势为先增后减再增，这是由价格和产能共同作用的结果。

4.2 模型分析

以某项目型制造企业大连分厂某年5～7月的订单及生产数据为样本进行仿真实验，验证定价方法的适用性和有效性。样本共包括91种产品，所需原材料情况、产品加工要求等数据见表2和表3。

目前企业采用以成本加成为基础的产品定价方法，通过成本历史数据对待加工产品的价格进行估算，其计算步骤如下：

(1)根据完全成本法计算产品i的制造成本C1i， 非制造成本C2i=C1i×ai/(1-ai)。

(2)单位利润Pi=(C1i+C2i)×bi/(1-bi)。

(3)产品i的单价即为Pi+C1i+C2i。 (ai,bi是一定的计提比率)

表2 大连分厂5～7月生产计划表

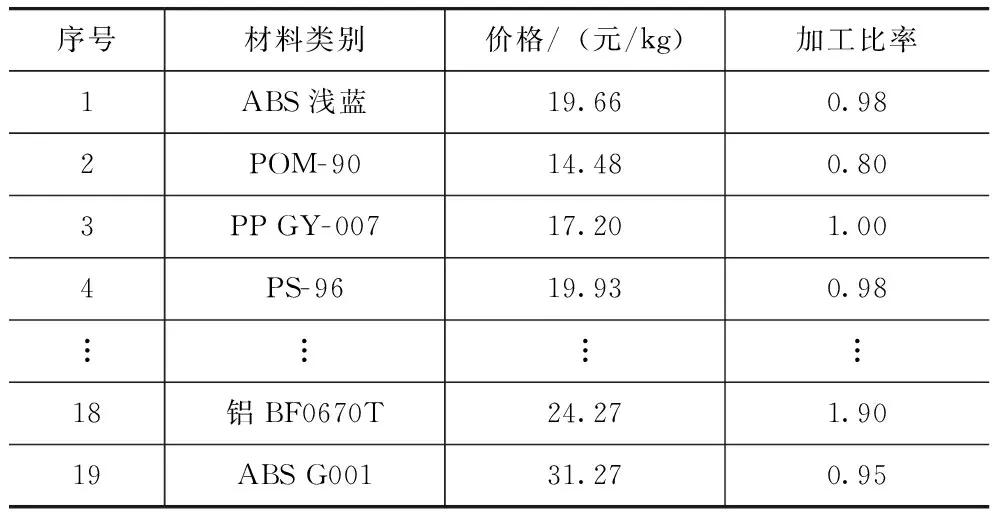
表3 生产材料

图1 产能对价格和利润的影响

采用以上两种定价方法优化价格，结果见表4(其中：①是本文方法，②是企业实际定价方法)。多数产品价格有效降低，整体价格重新优化。对应的，运用②方法时产品总利润为3 777 255元，平均质量85.1%；利用①方法利润总额达到4 984 359元，增加了31.96%，平均质量为98%，提高了15.16%；以第35种产品为例，价格降低了84个单位，利润目标提升了13.09%，质量提高了1.9个单位。表明本文定价方法可以有效优化产品价格，保证提高利润和产品质量。

表4 改进方法与企业定价方法结果对比

(续)

5 结语

随着市场竞争愈演愈烈，定价决策是否合理决定着项目型制造企业盈利能力的高低。结合客户的交货期和质量要求，按照一定的概率分布对随机需求进行模拟，在生产能力约束下以产品总利润最大、平均质量最高为目标，建立了多产品动态定价模型，提高了企业产品定价的准确性和合理性。基于蚁群算法设计蚂蚁的寻优启发式规则，通过数值实验证明此启发式规则能够保证双目标问题Pareto解的实现。最后通过实例验证了该定价方法能有效优化价格，提高产品利润和质量，为企业进行定价决策提供方法支持。

[1]刘希珍,魏祖龙.FAHP模型在项目型制造企业绩效评估中的应用研究[J].项目管理技术,2013,11(1):101-104.

[2]黄辉,梁工谦,肖茂.企业项目管理成熟度模型的构建与应用研究[J].管理工程学报,2005(S1):67-72.

[3]Granot D, Yin S. Price and order postponement in a decentralized newsvendor model with multiplicative and price-dependent demand[M].Linthicum：Informs, 2008.

[4]Mardaneh E, Caccetta L. Optimal pricing and production planning for multi-product multi-period systems with backorders[J]. Journal of Optimization Theory & Applications, 2013, 158(3):896-917.

[5]Chaharsooghi S K, Honarvar M, Modarres M, et al. Developing a two stage stochastic programming model of the price and lead-time decision problem in the multi-class make-to-order firm[J]. Computers & Industrial Engineering, 2011, 61(4):1086-1097.

[6]Palaka K, Erlebacher S, Kropp D H. Lead-time setting, capacity utilization, and pricing decisions under lead-time dependent demand[J]. IIE Transactions, 1998, 30(2):151-163.

[7]Deng S, Yano C A. Joint production and pricing decisions with setup costs and capacity constraints[J]. Management Science, 2006, 52(5):741-756.

[8]Zhang M, Feng J. Dynamic quotation of leadtime and price for a make-to-order system with multiple customer classes and perfect information on customer preferences[J]. European Journal of Operational Research, 2017, 258(1)：334-342.

[9]戴道明,杨善林.动态定价与允许需求延迟订货批量模型的联合决策[J].管理工程学报,2009,23(4):116-120.

[10]柏庆国,徐贤浩,潘伟.多分销渠道下易变质产品的联合库存与定价模型[J].管理工程学报,2017,31(3):84-92.

[11] Li H, Thorstenson A. A multi-phase algorithm for a joint lot-sizing and pricing problem with stochastic demands[J]. International Journal of Production Research, 2014, 52(8):2345-2362.

[12]Heuvel W V D. A polynomial time algorithm for a deterministic joint pricing and inventory model[J]. European Journal of Operational Research, 2006, 170(2):463-480.

[13]黄晶,杨文胜,李莉.随机需求下的交货期和质量关联定价决策[J].计算机集成制造系统,2016,22(7):1747-1758.

[14]Hu Z, Hu G. A two-stage stochastic programming model for lot-sizing and scheduling under uncertainty[J]. International Journal of Production Economics, 2016, 180:198-207.

[15]Tsay A A, Agrawal N. Channel conflict and coordination in the E-Commerce age[J]. Production & Operations Management, 2004, 13(1):93-110.

[16]García-Martínez C, Cordón O, Herrera F. A taxonomy and an empirical analysis of multiple objective ant colony optimization algorithms for the bi-criteria TSP [J]. European Journal of Operational Research, 2007, 180(1):116-148.

[17]邵建军,柯大钢,王军平.价格、时间敏感需求下的价格与交付期竞争策略[J].系统工程,2007(6):12-18. PMT