粒子群优化改进小波阈值函数的去噪研究

黄名钿+高伟

摘要：小波阈值去噪在信号处理领域应用非常广泛。针对传统软、硬阈值函数算法存在的缺陷，许多学者提出了介于软、硬阈值之间改进型阈值函数算法。但这些阈值函数在整个小波空间域内高阶不可导，存在临界阈值处不能平滑过渡的现象。因此提出一个带参数的阈值函数，可以实现临界阈值处的平滑过渡。同时，采用粒子群优化算法，针对信号含噪情况，自动优化阈值函数参数，实现去噪过程的自动寻优。采用基准信号仿真结果表明，提出的算法可以获得更小的均方误差和更高的信噪比，达到了去噪实用化的效果。

关键词：小波变换；粒子群优化；算法；阈值函数

O 引言

相关法、模极大值法和阈值法是小波去噪的三种常见方法，其中，阈值法最实用，已广泛应用于信号去噪中。阈值法有硬阈值和软阈值两种基本的去噪算法，但是这两种基本方法各有一定缺陷：一是硬阈值函数整体不连续，容易造成经小波去噪后的信号不平滑；二是软阈值函数整体上虽然连续，但是小波估计系数与含噪声信号的小波系数之间总是存在着恒定的偏差，这直接影响重构信号和原始信号的逼近程度。

针对软、硬阈值法存在的缺点，学者提Jq』了许多改进的阈值函数算法，这些算法介于软、硬阈值之间，通过改变阈值函数的参数可以有效避免传统阈值函数的缺陷，在整个小波空间域内，阈值函数虽然连续，但高阶不可导，在临界阈值九处曲线连续但不是平滑过渡。这种缺陷就可能导致在阈值去噪处理时会出现细节系数的过扼杀和信号振荡现象。

同时，对于改进的带参数的阈值函数算法，针对变化的实际信号，为了实现最佳的去噪效果，需要手动调节参数来处理新的含噪信号，限制了去噪算法对处理信号的适应性。针对这些问题，本文提出一个改进的阈值函数算法，可以解决阈值函数在临界阈值λ处不平滑过渡的问题，同时引用粒子群优化算法，实现阈值函数参数的自动寻优，让去噪算法自动适应处理信号的变化。

1 小波阈值去噪原理

小波阈值去噪的过程分为对含噪信号进行小波分解，高频系数的阈值量化处理和用小波逆变换实现信号重构三个步骤。其基本原理如图1所示：。

含噪信号经小波分解后，通常信号的系数要大于噪声的系数，选择一个合适的数九作为临界阈值，将小于该阈值的分解系数认为是由噪声引起的，予以舍弃；而大于该阈值的分解系数认为主要是由信号引起的，加以保留，这就是阈值去噪。在阈值去噪中，传统的硬阈值函数去噪之后存在着伪吉布斯（ Pseudo-Gibbs）现象，软阈值去噪则会造成恒定偏差问题，而其它的改进阈值函数算法存在着不平滑过渡等问题。为此，本文将对原有的阈值函数进行改进，以避免以上存在的问题。

2 新阈值函数的构造

针对硬阈值的不连续性、软阈值造成的恒定偏差、其他改进阈值函数的不平滑过渡现象，本文提出一种新的阈值函数：

新阈值函数：

其中k和cc为调节因子，且k和Cc为正数。

新阈值函数在小波域内和软阈值函数有着相同的连续性，克服了硬阈值函数在阈值处的不连续性，同时也避免了因不连续而导致的伪吉布斯（ Pseudo-Gibbs）现象；随着小波系数的增加，新阈值函数渐渐接近硬阈值函数曲线，这克服了软阈值函数中ω_j，k与ω_j，k之间总是存在着恒定的偏差的缺点；在/ω_j，k/>λ和/ω_j，k/<λ 范圍内，新阈值函数高阶可导，这种特性可以消除振荡现象，使重构信号显得平滑。

当k→∞时，新阈值函数就为阈值函数：

在此条件下，当α→O时，新阈值函数为软阈值函数，当a→∞时，新阈值函数为硬阈值函数；因此通过改变α值，新阈值函数可以在硬软阈值之间灵活变化。新阈值函数在硬软阈值之间，其参数k必须大于等于1，参数k决定了小波阈值的逼近程度，调节k使新阈值函数在阈值处理时能够保留一部分有用信号的高频部分，较好地抑制细节系数的过扼杀和信号振荡现象。

灵活调节k、α，新阈值函数曲线在硬、软阈值之间变化，如图2所示。对于不同的含噪信号，新阈值函数可以通过调节参数k、α，实现最佳的去噪效果。

3 粒子群优化算法

采用带参数阈值函数去噪过程中，针对具体含噪信号，可以灵活调节阈值函数的k和cc参数，满足不同信号处理的去噪要求。然而，在实际应用中，待处理信号的含噪情况是不可预测或不可知的。对于这种随机变化的含噪信号进行去噪，阈值函数的参数k、α应该也不可能是固定值。因此对于随机含噪信号的阈值处理，选择适用的优化算法来对阈值函数的参数k、α进行优化，以期能够适应信号的变化是去噪走向实用化的关键。

阈值函数有两个参数k、α，函数优化时参数较少，同时对于变化信号的处理则需较短时间内完成优化目标，因此，需要收敛速度相对高的优化算法。对比模拟退火算法、遗传算法、神经网络算法、蚁群算法等优化算法，选取收敛速度快、精度高及易实现且无需过多参数调整的粒子群优化算法。

3.1 PSO算法

粒子群优化算法实现简单有效，收敛速度快，算法中每个粒子代表一个待优化问题的可能解，并且分别由速度向量和位置向量来表征粒子当前的飞行速度和所在的位置。在每次迭代过程中，粒子通过个体极值和全局极值更新自身的速度和位置，即：

苴中为惯性权重，cl和c2的加速度系数，t是当前迭代次数，d是当前D维解空间，和订和r2是两个随机常数

3.2 适应度函数

利用重构信号的质量评价去噪算法的性能，采用PSO最小化原始信号和重构信号之间的均方误差。因此，对于改进的参数小波阈值去噪算法的适应度函数即为：

其中，f（i）是原始信号，f_m（i）是去噪后的信号，N是信号长度。

从式子（4）可以看出 ，适应度函数是由原始信号和去噪后的信号组成的，其中，去噪后的信号是由小波阈值系数进行重构的。根据式子（1），我们可以获得由阈值九和改变形状参数k、α 组成的新阈值函数。一旦阈值x和k、α 确定，阈值方案可以固定。根据阈值函数，可以获得阈值的小波系数，去噪后的重构信号可以确定。因此由x和k、α 组成的矢量可以看作该PSO算法的粒子位置。通过最大限度的减小适应度函数值获得相对应的适应度值。endprint

4 利用PSO算法进行小波阈值信号去噪

以下是基于粒子群优化算法的改进小波阈值函数的信号去噪步骤。

步骤1：根据相应参数设置，初始化PSO的搜索空间和位置。本文采用以下例子进行说明：小波变换中，例如在db系列（db3～db6）中选取小波，分解层数设为n（ 1～10）。根据信号和噪声的特性采用分层阈值法，不同分解层数应设置不同阈值。粒子位置由阈值和形状调整参数组成。算法选取小波基函数和分解层数，粒子位置是进行（n+2）维空间的初始化，即（λ₁，λ₂，λ₃…λ，α，k）。阈值（λ₁，λ₂，λ₃…λ，α，k）初始化为1～160，α和k初始化为0～100。一般群体大小应为搜索维数的两倍或两倍以上，因此由本文中的问题，考虑群体大小为20。

步骤2：根据式（4）计算每个粒子的适应度值F。第i个粒子的适应度值表示为Fid；

步骤3：使用（2）和（3）更新粒子的速度和位置；这两个方程的不同常数和变量应该初始化为如下：

（1）常数rl，r2独立地均匀分布在[0，1]的范围内。

（2）惯性权重ω，调整权重系数的大小，可以使粒子群跳出局部极小值，ω取值在0.1至0.9之间。

（3）X tid和Vtid分别是第i个粒子的第d维位置和速度；其中Xtid如步骤l中所述被随机初始化，并且Vtid在搜索空间中被随机初始化。

（4） Fib和Fgb分别是第i个粒子的个体最佳适应度值和全局最佳适应度值。如步骤2中所讨论的初始化值Fib，Fib的最佳值被当作全局最佳初始化值Fgb。

步骤4：限制更新的速度和位置。如果在（-Vmax，+Vmax）范围外发现新速度，则将其限制为边界值。同样的，对于位置的更新，使用相同的方法来处理新位置。

步骤5：计算新位置的适应度Fid。如果当前Fid优于先前的Fib，则Fib由当前Fid替代；否则，保留以前的Fib。如果当前Fib比先前的Fgb更好，则Fgb由当前Fib替代；否则，保留先前的Fgb。类似地，个体最佳位置Pid和全局最佳位置Pgd被相应地更新。

步骤6：重复上述步骤3-5，直到达到终止条件或最大迭代次数。

图3给出了基于PSO优化带参数小波阈值函数去噪方法的流程图。在该图中，对于待处理的噪声信号进行小波变换（ SWT）分解，得到小波分解系数SWA和SWD，SWA和SWD分别表示通过小波变换（SWT）获得的小波近似系数和细节系数。其次，对于细节系数（ SWD）进行粒子群优化。先设置粒子群算法的初始值，粒子个数、常数、惯性权重、最大速度等，在满足控制变量约束条件下，随机赋予种群中每个粒子的初始位置和初始速度。根据适应度函数计算并评价每个粒子的适应度值，设定粒子的初始局部最优值和全局最优值。通过比较粒子的当前的最优值和历史的最优值，更新粒子的局部最优值和全局最优值。根据式子（2）和式子（3）更新粒子的速度和位置，如果粒子的速度大于Vmax，则取Vmax。如果满足迭代终止条件。由对应于最佳的适应度值的结果参数，对对应的小波系数进行阈值化处理，利用阈值化后小波细节系数和小波近似系数进行小波重构，得到去噪后的信号。

5 数据仿真与结果

可以采用多个指标来评估阈值去噪方案相对于重构信号质量的性能。本文采用的指标是信噪比和均方误差两个。信噪比（ SNR）如（5）所示：

其中f（i）是原始信号，f'（i）是去噪后的信号，信噪比SNR提高越大，表示信号去噪效果越好。

5.1 仿真设置

以下对两种不同噪声振幅的基准信号进行仿真去噪，实验结果对比去噪的效果，来验证整体自动寻优的基于粒子群优化带参数小波阈值函数的去噪效果优于新阈值函数的去噪效果。这两种基准信号分别是从众所周知的Bumps和Doppler信号，含噪信号的信噪比设置为10分贝（ dB）。仿真平台采用基于Windows7系统的MATLAB R2013a软件。原始信号的总样本为2048，最大迭代次数设置为50。

5.2 仿真结果与分析

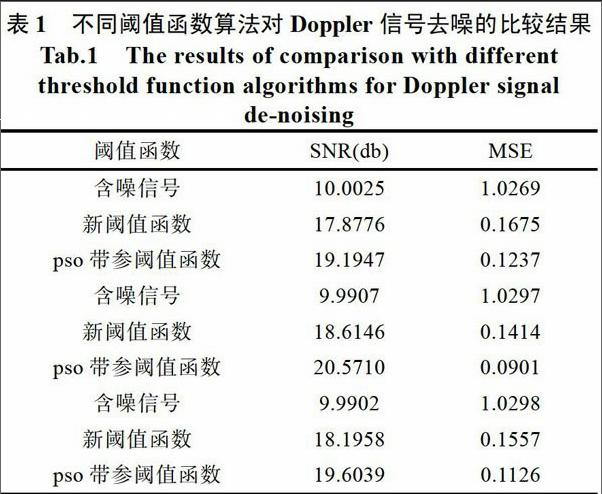
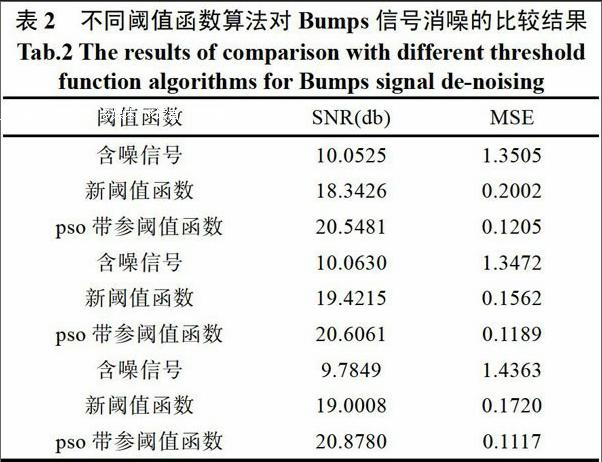
分别对Bumps和Doppler信号进行仿真，运行算法，生成含噪信号去噪前后的效果图，同时在workspace查看变量数据，显示含噪信号去噪前后的信噪比和均方誤差值，对比实验结果数据，并进行结果分析。实验仿真结果显其去噪后的效果图4和图5、数据表格表l和表2。

由图4和图5可以看出，基于pso优化的带参数小波阈值函数法对含噪信号去噪获得的曲线更接近于原始信号，重构的信号更好地反映原始信号的细节信息。因此，所提出的基于pso优化的带参数小波阈值函数法去噪效果更好。

根据均方误差（ MSE）和信噪比（SNR）作为评估信号去噪效果的标准，MSE值越小和SNR提高越大表明信号去噪效果越好。

从表l和表2中的数据可以看出，基于pso优化的带参数小波阈值函数法对含噪的Doppler和Bumps信号进行去噪后，其得到的MSE参数值比新阈值函数法得到的值小，并且，其得到的SNR参数值比新阈值函数法得到的值大，这些数据清楚地表明，所提出的基于pso优化的带参数小波阈值函数法去噪效果比新阈值函数法更好，基于pso优化的带参数小波阈值函数法是一种有效的滤波器。

6 结论

本文中，提出一种采用基于pso优化的带参数小波阈值函数的信号去噪方法。通过仿真实验，得出以下结论：带参数的新阈值函数能够克服小波阈值函数去噪方法存在的缺陷，调节参数使之兼具硬、软阈值函数优点，并在临界阈值内添加平滑过渡区，可在阈值处理时保留一部分有用的高频信号，较好地抑制细节系数的过扼杀和信号振荡现象。针对随机含噪的信号，采用基于pso优化的带参数小波阈值函数法，可以实现阈值函数参数的自动寻优，确定最佳的小波基函数和分解层数，获得最佳的去噪效果，达到去噪算法自动适应处理信号的变化之目的。endprint