关于树木生长时间因素影响剔除的研究
杨科家,艾秋月,陈志敏,王佃良,束德翠,杨国云
(1.山东省莒县林业局,山东 日照 276500;2.山东省航空护林站,山东 济南 250014;3.莒县小店镇林业站,山东 日照 276500)
影响树木生长的因子主要有光照、降水和气温三大因素,笔者经过近20年的悉心研究,以时间要素为尺度进行了它们对树木生长的影响的研究及其交互作用的研究,并建立了经验方程,但有的学者认为需要把时间要素的影响要予以剔除,至今没有见到各种因子(包括时间)剔除试验的报道,笔者所做的试验研究都是在假定其他因子表现基本稳定的前提下进行,毋须作什么因子影响剔除,笔者现就这一课题进行研究,以时间因素的剔除对降水量对树木影响研究为例进行。
1 资料来源
历年降水量资料由烟台市牟平区气象局提供,解析木材料来自2013年3月中旬笔者采自烟台市牟平区昆嵛山林场2株生长正常的赤松解析木,分别为65年生和45年生;风云林场2株生长正常的赤松解析木,分别为77年生和61年生。树高超过10 m的,胸径段用2.6 m区段,其他采用2 m区段,分别在树高5 cm(0盘)、1.3 m、3.6 m、5.6 m、7.6 m、9.6 m处截取圆盘,树高不到10 m的,采用1 m区段,5 cm(0盘)、1.3 m、0.5 m、1.5 m……9.5 m处截取圆盘,通过干燥(风干)、打磨,用高分辨率扫描仪进行彩色扫描,并将扫描好的图像放入CAD操作平台中进行量测,并用实测资料进行校正,分别量取南北径和东西径,并以5年龄阶进行交叉定年,数据精度为0.01 cm,量取各树盘各年度的树木直径,并根据有关测树学技术原理,推算树高和材积。
2 研究方法
经过笔者近20年来的研究,树木生长量、生物量、碳储量均与树龄及年降雨量表现出十分明显的相关关系,而且凡是线性相关关系显著的,其对数值表现更为显著的相关性。笔者充分吸收和利用巩延苹、张靖等人的研究成果[1-6],经过悉心研究,用经验方程y=exp(a+bx)用来判断因变量y随自变量x的变化程度(变化速度),其中y为树木的生长量、生物量、碳储量等指标,x为树龄及年降雨量等自然因素指标,a,b为待求系数(下同)。用经验方程y=exp(a-b/x)来寻求效益指标最大化,即用最少的投入(包括时间)以求获得最大的收益。笔者经过研究,通过以每一年为研究对象,对方程进行拟合试验,结果除个别指标表现出相关关系显著外,大部分指标相关关系不显著,但是通过累加效应(即用累计生长量与树木年龄、降雨量累加量等建立回归相关方程),则表现出十分显著的相关性,笔者认为有许多研究人员用5年滑动的办法,使回归相关系数大大提高,事实上就用5年的数据累加,只不过是取了5年的均值而已,事实是这种做法只是提高回归精度的一种办法,其科学含义就不准确了,笔者采用累加效应具有十分明确的科学含义。例如树木生长量和树木年龄。树木年龄即时间的累加量,树木生长量累加,即树木总生长量。而用5年滑动的办法处理数据,是用5年的均值代表中间年份的数据指标,我认为是有点牵强附会,用5年滑动的办法,对于首尾两端的数据就不好处理了,因为缺乏数据支撑,但是对于研究上百年上千年的数据变化还是可以的,可以将两端数据舍弃。笔者充分利用累加效应,不仅弥补了滑动处理理数据的不足,而且更能显示其科学含义,而且计算量相对小一点。
先用经验方程y=exp(a+bt)和y=exp(a-b/t)建立树木生长量与树木生长年龄的回归关系,求得待求系数,再用经验方程y=exp(a+bp)和y=exp(a-b/p)求得树木生长量与年降雨量的回归系数,再用树木年龄的回归方程计算结果对降雨量回归方程进行技术修正,所有过程均要进行检验和校验。
由于各因子对树木生长的影响是一种乘数效应,也就是一种指数效应,利用经验方程指数降阶的办法,对其进行因子剔除的研究,根据以上论述笔者将经验方程yc=exp(a+bx)指数函数(yc为方程拟合值,a,b为待求系数)命名为成长方程(又叫发展方程),将yz=exp(a-b/x)复合函数(yz为方程拟合值,a,b为待求系数)命名为阻力方程。假若y为树木生长原值(实测值、计算值),则用yjc=〔y^(nc+1)〕/yc^nc其中nc为大于1的实数,单位为倍,称为消除影响倍数值,简称倍数,通过电子表格试算求得(下同)方程在各个时间尺度上的试验结果,进行因素成长力剔除的研究.同样地利用yjz=〔y^(nz+1)〕/(yz^nz)(其中n为大于1的实数,单位为倍)方程在各个时间尺度上的试验结果,进行因素成长阻力剔除的研究。其中倍数nc和nz值的确定,以其试验精度刚刚达到95%以下,即认为该因素的影响被剔除,其中倍数越大,表明该因素对树木生长的影响越深刻、越强烈,否则就越肤浅、越弱化。再根据其影响程度加权,用方程ycz=〔y^(ncz+1)〕/[p*yc^ncz]/(q*yz^ncz)其中ycz为成长和阻力共同剔除的方程拟合值,p,q分别为成长和阻力影响的权重,用yjc和yjz方程拟合,当精度刚刚低于95%的倍数加权值。其中p=nc/(nc+nz),q=nz/(nc+nz),不难理解p+q=1,ncz是指用方程以ycz为变量,以其他影响因子为自变量,建立成长方程拟合,当试验精度刚刚低于95%的倍数取值。
3 研究过程
经过研究发现,对于经验方程y=exp(a+bx)的演算,当x的所有数据同时加上或减去同一数值,试验结果只是a值变化,b值和用来检验的t值、F值、R值及试验精度保持不变,因此通过这一方程,来实现以往没有实际记载数据的重建成为可能,而保持现试验的精度不变。
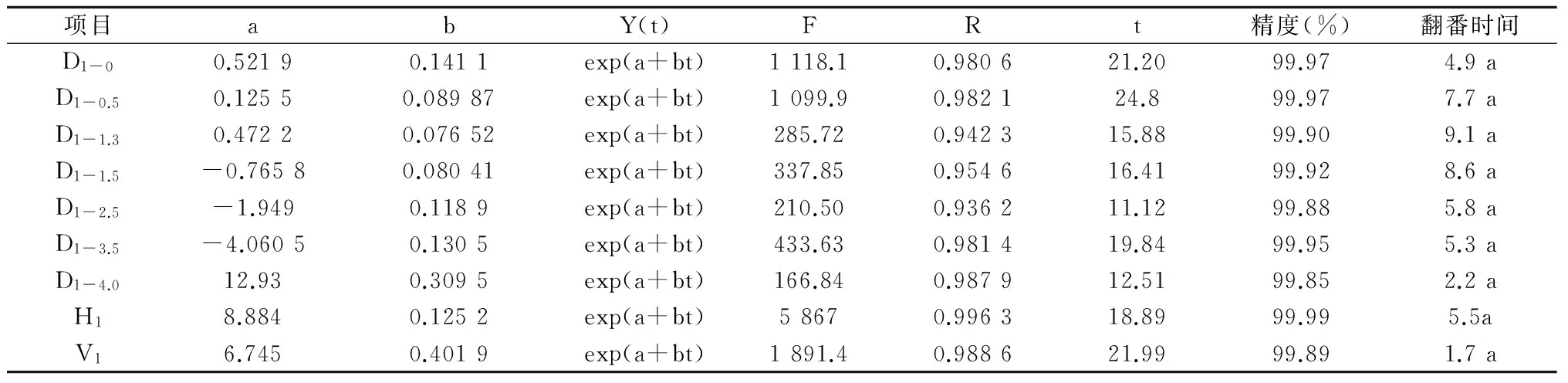
表1 45年生赤松生长量与时间经验方程拟合表(成长方程)
先用每年树木生长量因变量y(t),以时间t为自变量,分别以成长方程和阻力方程建立函数关系,通过回归分析,试验结果见表1、表2,其中长度单位为cm,材积单位cm3,用D1-0和D1-0.5分别代表0盘和0.5 m(树高处)的树直径值,以此类推,用H1代表树高,用v1代表树木材积(下同)。 从表1可以看出,树高越高树径生长越快,树高与树径增长速度基本相当,树木材积和树木D1-4.0递增速度基本一致,是其他树径和树高平均递增速度的30%左右。
按照2节介绍的研究方法,在进行成长方程时间作用剔除试验时发现,成长方程的待求系数保持不变,而试验精度有所降低;相反的阻力方程的待求系数有所变化,其试验精度有所提高或远远高于成长方程的试验精度。反之,在进行阻力方程时间作用剔除试验时发现,阻力方程的待求系数保持不变,而试验精度有所降低;相反的成长方程的待求系数有所变化,其试验精度有所提高或远远高于阻力方程的试验精度。
从表1可以看出,所有试验均以超过99.85%精度通过试验检验,树高项目到了99.99%的精度,除1.3 m和2.5 m径试验精度略低于原试验精度外,其余项目均高于原试验精度,说明试验设计的合理性。表1的翻番时间含义为该指标递增一倍的时间(下同)。

表2 45年生赤松生长过程经验方程拟合表(阻力方程)
从表2可以看出,除0.5 m、1.3 m、1.5 m、3.5 m径项目外,其余项目均高于原试验水平,低者也相差不大,所有项目均以99.82%以上的精度通过验证,许多项目的试验精度已接近100%,说明试验路径的选择是正确的。表中tm为在该时间点上该项目平均增长速度最快,即理论上的数量成熟龄,tz的含义为该项目的即时增长速度最快(下同)。

表3 45年生赤松生长量与降雨量经验方程拟合表(成长方程)
从3可以看出,各项目均以高于99.79%的精度通过试验验证。在样本数大于28的前提下,试验精度均高于原试验精度(不剔除时间因素影响,下同),这就表明该试验技术路径的设计是十分科学合理的,为了保证试验精度,增加试验样本数量是何等的重要。除材积项目外,试验精度均有所降低,是由于年际降水量的分布不均造成的,表明时间对树木的影响更为强烈。除树高项目外,变化速度(树木生长速度)均有所提高,说明降水乃是影响树木生长的十分活跃的因素。

表4 45年生赤松生长量与降雨量经验方程拟合表(阻力方程)
表4的试验结果表明,样本数为最大,达到42时,其试验精度比原试验有所降低外,其余均有所提高,试验表明随着树木高度的升高,其径值的方程b值有逐步增大的趋势,这就表明树木生长有多次生长高峰的可能,这有待在以后的研究中另立课题进行研究。所有项目均以高于99.61%的精度通过检验,说明试验具有较高的可靠性。
表1~表4的试验表明,利用此种方法可以降低时间因素的影响作用,时间影响作用的降低,反而会使降水量对树木生长表现出增强的效果。
4 试验方程的适用性检验
笔者用同样的方法对另外一株样木进行了试验,取得了较好的试验效果,以此株样木试验结果对以上的试验结果进行适合性检验。检验结果如表5所示。表中FZ-2与FZj-2分别代表发展方程树龄因素剔除前后与2号样木比较的F值,FH-2与Fhj-2分别代表阻力方程树龄因素校正前后与2号样木的F值,表中FpZ-2与FpZj-2分别代表发展方程树龄因素剔除前后与2号样木降水量影响比较的F值,FpH-2与Fphj-2分别代表代表阻力方程树龄因素校正前后降水量影响与2号样木的F值,D0代表地径项目,余者类推。

表5 经验方程适合性检验表
通过查表,时间的影响在不剔除任何因素影响的前提下,两样木之间大部项目方程拟合值均无显著性差别,只有个别项目有显著差别,但是不是差异极显著,说明时间经验方程的应用是十分科学合理的。时间的上升和阻力作用被部分剔除后,其时间的发展和阻力方程及其降水(包括时间因素的作用部分剔除前后)的发展和阻力方程的影响,表现出十分强烈的差异性,大部分差异极显著,只有极个别项目4.0 m径表现没有明显差异,这就表明降水相对时间因素来说是一较活跃的影响因素。
5 讨论
经验方程的应用,事实上就是把时间也看成一个变量,一种物质的存在形式。辩证唯物主义认为,时间和空间都是物质的存在形式。笔者在试验区组设计时,往往只把空间(地段)分成若干小方,然后施加不同当量的影响,从其随着时间的推移而表现出的差异,进行各种试验数据分析,找出其规律。然而,笔者借助树木生长年轮的特征,以时间为依托(依据)进行区组划分,这样由于对同一株树木进行试验分析,在客观上避免了因立地条件的差异而造成的噪声。传统意义上的因子影响试验,以空间区组设计,很难避免因立地因子的差别而造成的客观误差,单因子试验还能进行(与对照比照),多因子及交互作用试验效果更不会理想。笔者利用经验方程试验,事实上就是把时间尺度作为区组设计的依据,完全避免立地因子造成的偏差,时间对树木生长的影响,主要是由树种的本身生理特性所决定的,是否需要去除有待研究。研究表明各因子的交互作用,是一种叠加效应,是乘数效应(指数效应),而不是加法效应,笔者的传统思维应是加法效应,试验表明利用加法效应的思维和做法,试验精度降低,可操作性差,因此笔者必须打破旧的模式、框框,与时俱进地开展科研工作。以时间换空间、以空间换时间在军事和社会人生实践中得到了广泛应用,层出不穷,不胜枚举,因此笔者在科学试验上以时间换空间的做法徝得一试。
通过研究得出以下结论,通过此种方法能够剔除时间因素的部分影响,但是不能完全剔除,因为时间因素的作用虽然是由于树木本身特性决定的,但是时间的影响乃是光照、气温、水分等诸因素的共同作用的结果在时间尺度上的表达,利用经验方程剔除时间因素的作用的同时,也将其他因素的作用作了部分剔除,至于用何种办法才能完全剔除时间因素的影响,那就是更为复杂的研究课题,有待随着科学技水平的发展,科学手段的改进,逐步得以解决。研究表明降水比时间对树木生长的影响是更为活跃的因子。由于利用该种方法,使试验精度有所提高,并可使阻力方程和发展方程的研究精度相接近,这就证明了笔者定义的阻力和发展方程的合理性。笔者经过本研究及其他长期研究认为,树木生长存在二次或多次生长高峰的可能性,并不是以前传统意义认为的树木生长高峰只有一次。笔者认为,虽然说通过该种方法,可使试验精有所提高,但是不能完全剔除时间因素的影响,只能部分剔除,虽然以此种方法继续剔除下去,试验精度还有所提高,但是笔者认为实际意义并不很大,只要在保证实试验精度的前提下,可以不进行时间因素影响剔除处理,除非是对于极其珍贵,经济价值极高的树种才有实际意义,因为该研究需要大量的人力、物力、财力的投入,还需要较长的研究时间,研究和计算过程也较为复杂,在这里只是知道其中奥妙就可以了。
[1] 巩延苹.黑赤松生长与年降水量关系研究[J].防护林科技,2017(6):41-47
[2] 张靖,于凌飞,王一辰,等.赤松生长节律与降雨量关系研究[J].防护林科技,2017(11):38-42
[3] 廉丽姝,李为华,朱平盛.山东近40年气候变化特征[J].气象科技,2006,34(1):57-59
[4] 高卫东,袁玉江,张瑞波,等.树木年轮记录的天山北坡中部过去338a降水变化[J].中国沙漠,2011,31(6):1535-1540
[5] 刘国杰.注册咨询工程师(投资)执业资格考试教材复习指导[M].天津:天津大学出版社,2003
[6] 赵西平,郭明辉,朱熙岭.温度对树木生长与木材形成影响的研究进展[J].森林工程,2005,21(6):1-4,31

