盾构隧道衬砌荷载取值反演分析

王晓强，屈兴兵

（1.洛阳理工学院土木工程学院，河南洛阳4710232；2.中铁隧道勘测设计院有限公司，天津300133）

岩土工程中，所谓反分析法，是以现场量测到的某些物理信息量(如位移、应变、应力或荷载等)为基础，通过反演模型(系统的物理模型及其数学描述，如应力与应变关系式等)推算得到该系统的各项或某些初始参数(如初始地应力、本构模型参数等)的方法。其目的是建立接近现场实测结果的理论预测模型，能较正确地反映或预测岩土结构的某些力学行为。

在正分析中，已知作用在结构上的荷载，可以方便地计算出结构的内力，并可以绘制出结构的荷载—内力关系曲线，很直观地反映出结构的荷载响应。基于这一点，若是量测得到了结构的内力，可以通过荷载内力计算理论，得出相应的荷载值。

1 工程概况

我国东南沿海某核电站1号、2号取水隧洞平面轴线为2条平行直线，隧洞最大埋深约55.75m。隧洞主要采用盾构法施工。隧洞内径7.3m，外径8.7m，采用盾构管片和二次衬砌复合支护结构。其中盾构管片厚度0.4m，作为隧洞的主体结构，二次衬砌厚度0.3m。盾构隧洞采用一台泥水平衡式盾构掘进。

隧道全断面主要位于可塑—硬塑的粘土层中，属Ⅳ类围岩。

2 衬砌荷载反分析确定

2.1 荷载的种类

盾构隧道的衬砌结构不仅要保证运营阶段安全，而且要确保施工过程的安全。对于衬砌结构计算理论，特别是荷载—结构法，需要确定所有荷载种类，根据隧道的不同工作状况，进行荷载不利组合，计算截面内力。

根据施工期和运营期的受力状况不同，将衬砌的受力过程分成不同的工况分析。本文中衬砌结构设计受力主要依据施工期工况，即：外管片施工期管片自重、施工期荷载及全部水土压力由外管片环单独承担。

作用在该隧道结构主要的荷载为：垂直和侧向的土压力和水压力。因此，准确地计算出隧道结构的土压和水压是结构优化设计关键步骤。

2.2 土压力荷载计算

在盾构隧道管片设计中岩土压力的计算方法存在较多不同看法，比如水土分算和水土合算的选择、竖向土压力选择松弛土压力和全覆土重、水平土压力选择静止土压力和朗肯主动土压力等问题，这些问题都说明盾构管片土压力的研究还有待深入。

土压力的影响因素较多，它不仅与地层的物理力学性质、衬砌的刚度有关，而且与施工工艺、隧道的埋深、直径、形状等几何参数有关。除此之外，还与盾构施工方法密切相关。附在管片表面的土压力计容易受到盾构施工过程的损害，使得盾构管片土压力的实测值的可靠性不高。随着隧道埋深、盾构断面的加大以及大量复杂地层中施工项目的出现，现有的管片设计荷载确定方法能否保证管片的安全有不确定性，因此发展符合盾构工程实际的管片土压力计算方法是管片设计中的一个重要研究课题。

迄今为止，有关盾构管片土压力的研究多偏重于经验性的总结，按其所采用的原理的不同，目前确定衬砌土压力常见的方法有理论计算和现场量测等。

2.2.1 理论计算

一般将作用于衬砌上的土压力分为垂直地层压力、水平地层压力、管片底部的垂直地基反力以及由衬砌变形引起的地基抗力（弹性抗力），如图1所示。

（1）垂直土层压力全覆土重理论。根据静力平衡条件，认为垂直地层压力是上覆土柱的重量减去两侧地层对柱体产生的反向摩擦力，在较软弱的土层中，由于内摩察角很小，此摩擦力可假定为零，即：

Pv=γh

式中：Pv——垂直地层压力，kPa；

γ——上覆土层的平均容重，kN/m3；

h——上覆土层的厚度，m。

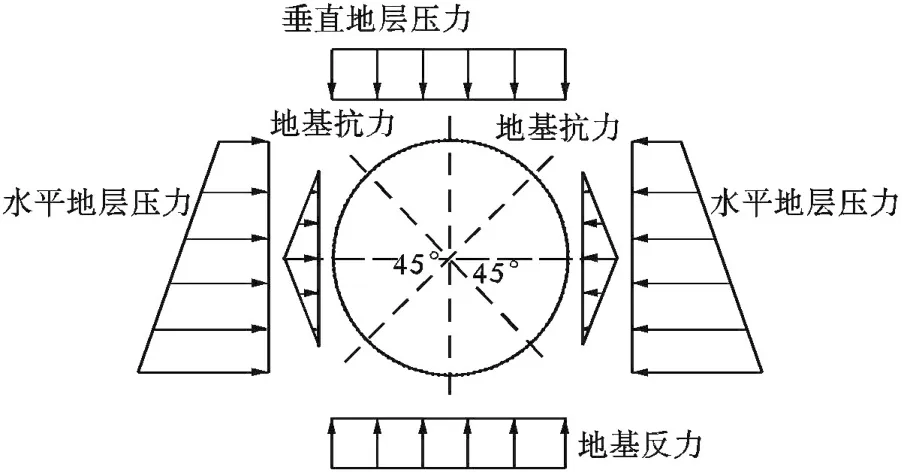
图1 衬砌管片受力示意图

资料表明，在软土地层中，竖向土压力在隧道拱顶部分随时间延长而增大，最后十分接近于上覆全部覆土重量。当隧道的埋深较大或土质较坚硬时，土层的反向摩擦力不可忽略，其计算结果是不合理的，实测资料表明在粘土地层中衬砌的竖向荷载比全覆土重理论计算值小得多。

（2）垂直土层压力太沙基松动土压力理论。太沙基理论以松散体压力理论为基础，从应力传递的概念出发，考虑了洞室尺寸、埋深、粘聚力和内摩擦角对士体稳定性的影响，由平衡关系式推算出垂直地层压力的计算公式。

太沙基理论考虑了隧道断面的几何尺寸、埋深、土体的强度指标等对土压力的影响，它假设隧道开挖后从隧道两侧延伸至地面出现2个剪切面，衬砌顶部的土压力为这2个剪切面所围的土体自重减去两侧面上的剪切力。同时它也考虑了土体抗剪强度随深度的变化。

2.2.2 现场量测

隧道衬砌管片设计理论最大的问题在于能否正确地反映盾构管片与周围土体的相互作用；衬砌外荷载的数值大小和分布情况与隧道埋设地层的水文地质情况、施工方法、衬砌本身的刚度等有密切的关系。对于这些复杂的影响因素，简单的采用某一计算理论很难真实反映工程实际，因此，本文通过现场量测的方法，利用土压力盒、孔隙水压力计等直接量测作用在隧道上的地层压力，用不同计算理论进行分析，对盾构管片周围水土压力的分布规律进行探讨。

现场量测能够反映各种因素对土压力的综合影响，因此现场量测数据的收集和分析是结构设计的重要依据。现场量测是较好的研究手段，但是由于其影响因素众多、实测本身的误差，以及土压计本身的精度问题，实测的结果仅有参考价值，仍然不能非常有效地反映实际的土压力分布情况。

2.3 盾构隧道土压力计算

根据隧道覆土厚度、地质条件等，采用全覆土重理论、太沙基公式(松动土压力)等进行计算。在施工过程中量测作用于隧道管片衬砌结构实际土压力，据此检验和修正采用的设计计算荷载取值。相应断面的土压力理论计算值与实测土压力的比较如表1所示，根据表中数据理论值和实测值有一定的差值。

从表1可以看出，基于3个断面的实测和计算数值，浅埋部分太沙基松动土压力理论计算值和全覆土土压力计算的土压力值均小于实测数据，浅埋隧道注浆时与稳定时实测土压力分别是松动土压力计算值的1.32～3.2和1.11～2.85倍、注浆时与稳定时实测值是全覆土土压力计算值的1.09～1.82和0.87～1.53倍；深埋部分注浆时与稳定时实测土压力是松动土压力计算值的0.66～2.16和0.48～1.77倍、深埋部分注浆时与稳定时的实测土压力是全覆土土压力计算值的0.57～1.33和0.90～1.21倍，盾尾注浆压力是施工过程管片外表面受到的最大外部荷载。根据表1数据结合土层性质，深埋段采用太沙基松动土压力理论计算更为合理。不同埋深段测试数据显示，浅埋段围岩相比深埋段的围岩压力要大一些。围岩压力沿断面分布表现出一定的随机性，但从整体统计的均值来看，围岩压力分布还是比较均匀的。

2.4 衬砌外荷载反分析计算值与实测值对比

根据实测值分析可知，对于泥水平衡盾构，在施工阶段由于管片背后注浆等因素的影响，使得主动土压力和静力平衡计算得出的隧道拱顶、拱腰以及拱底处的压力值与实测值之间的偏差较大，最大值差值达到30%以上。因此，根据上述理论来计算施工作用下软土隧道上的荷载，是会产生很大的误差，根据对实测值的分析，隧道拱顶与拱腰之间任意点径向作用荷载的变化规律为余弦变化，满足关系式：

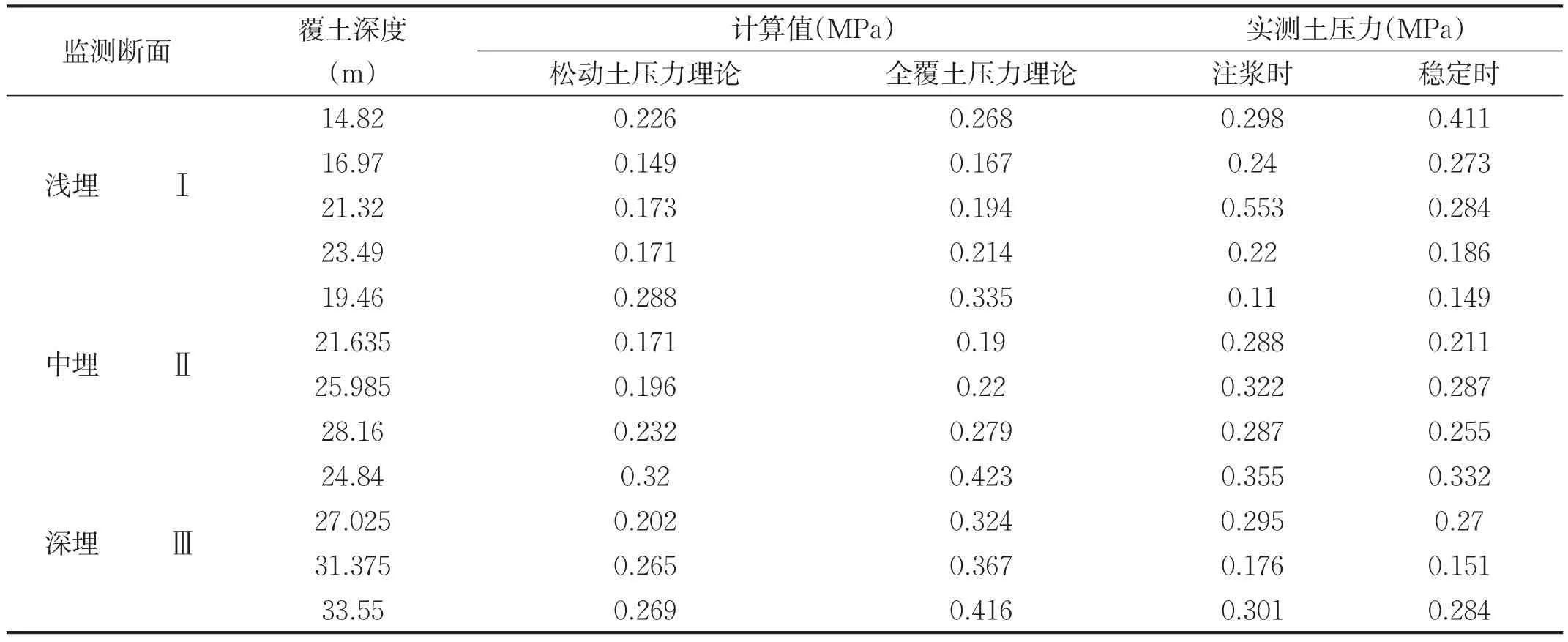
表1 实测值与理论值比较

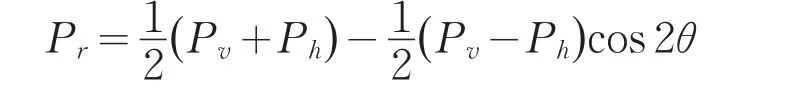
式中：θ——与拱腰处水平轴的夹角；

Pv——隧道顶（底）点径向作用荷载；

Ph——隧道水平点的径向作用荷载。

计算结果如表2所示。

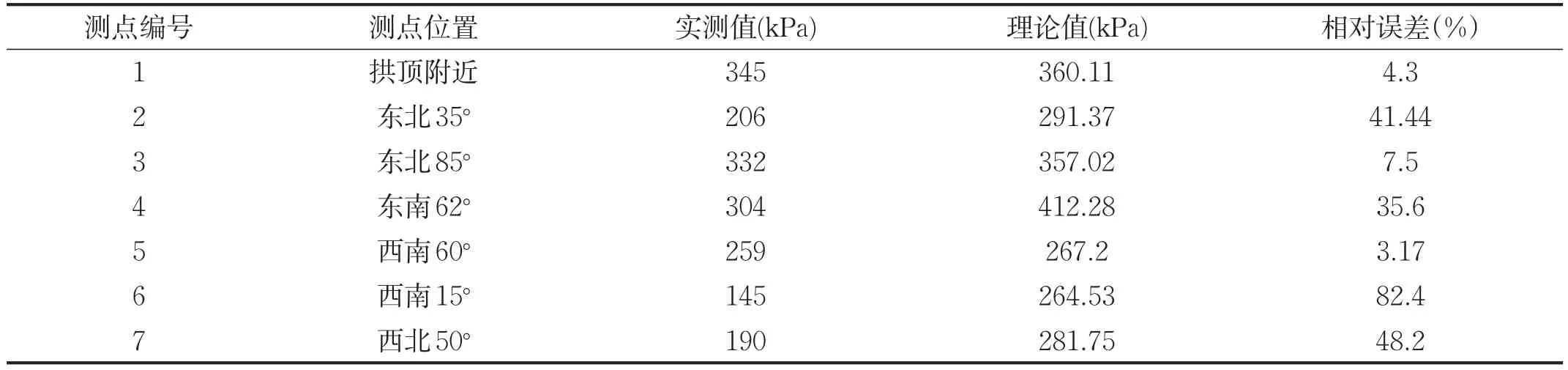
表2 施工阶段土压力实测值和反算值比较

由表2的数据可以看出，根据上述提出的假设，拱顶与拱腰处的反算值与量测值之间吻合的较好，但拱底的吻合却并不理想。拱底实测值明显小于拱底围岩压力值，而利用静力平衡原理计算隧道拱底值应明显大于拱顶值，说明衬砌结构土压力受注浆压力、施工条件和地质条件等多方因素的影响较大。

虽然上述假设对管片局部受力分析吻合的较好，能够反映施工阶段隧道上的荷载分布形状，但为更好地定量反映整个管片受力特征，需要采取其它手段进行进一步的模拟分析。

3 小结

（1）通过衬砌结构注浆时与稳定时实测土压分别与2种理论（全覆土重理论、太沙基公式）计算值比较可知，盾尾注浆压力是施工过程管片外表面受到的最大外部荷载，设计时需要重点考虑。浅埋部分（埋深小于2倍隧道跨度）采用全覆土土压力与实测土压力较为接近，依据土层特性，深埋部分采用太沙基理论计算较为合理。

（2）由于衬砌结构土压力受注浆压力、施工条件和地质条件等多方因素的影响较大，为了更好地显示整个管片受力特征，需要采取其它手段进行进一步的模拟分析。

本文认为应该寻找简单易行而又相对准确的反分析方法，能够方便地应用于工程现场计算参数的反分析，通过该分析方法，能够采用“初步设计—现场监测—反演分析—调整计算参数、计算方法—再设计”这一循环过程，提高工程设计的合理性和可靠性。

[1]吉林,赵启林,冯兆祥,等.岩土工程中反分析的研究进展[J].水利水运工程学报,2002(4):57-63.

[2]陈方方,李宁,张志强,等.岩土工程反分析方法研究现状与若干问题探讨[J].水利与建筑工程学报,2006(3):54-58.

[3]张世殊,裴向军,魏小佳,等.狮子坪电站二古溪1#隧道变形破坏特征及结构荷载反分析研究[J].岩石力学与工程学报,2014(11):2283-2290.

[4]宋玉香,贾晓云,朱永全.地铁隧道竖向土压力荷载的计算研究[J].岩土力学,2007，28(10)：2240-2244.

[5]杨志法,王思敬,等.岩土工程反分析原理及应用[M].北京:地震出版社,2002.

[6]刘艳清,卢汝绥.软岩隧道围岩压力的位移直接反演方法的研究[J].土木工程学报,2001,34(1):84-87.