川西大山区检波器组合高差研究——以龙门山为例

雷扬，吴闻静，李颖，周德帅，刘胜

（1.中石化石油工程地球物理有限公司南方分公司，四川成都610041；2.中石化石油工程地球物理有限公司南方分公司德阳中心，四川德阳618000）

川西龙门山地区受构造运动影响，呈现出典型的地表、地腹“双复杂”的地震地质特征，获得能够较好反映地下构造特征的地震资料难度较大。复杂的地表结构导致干扰波异常发育，种类繁多，能量差异相对较大，其中以面波、散射波等次生线性噪音最为典型，这类强干扰波频率从低至高、能量从弱至强均不同程度存在于单炮记录中，对有效反射压制明显，这类地区干扰波发育是影响地震资料品质的重要因素之一，针对龙门山山前带，开展了多期次地震采集攻关，但是在解决龙门山及山前带隐伏构造区成像问题上仍然具有较大缺陷，尤其是作为关键基础环节之一的大组合基距接收技术一直因大山区对组合高差限制而未获得有效突破，龙门山地区剖面成像效果极差，构造解释不可靠。

本轮地震采集工作重点针对大组合基距接收的瓶颈组合高差限制开展了攻关，凭借前人认识、经验及理论计算公式进行了理论分析；建立了符合区域特征的理论模型，开展理论模型的正演模拟记录对比分析；在现场开展了一系列系统化的组合高差对比试验，并进行了定性、定量的对比分析；结合理论分析、模型分析、实际资料分析总结出了龙门山地区组合高差的适应范围可放大到25m，为大组合基距接收技术奠定了基础，大大促进了剖面成像效果改善，增强了龙门山山前带构造解释精度；通过理论分析、现场试验结果对比分析，总结了龙门山地区最大组合高差计算中速度、波长范围的合理值。

1 组合高差理论计算

根据目前的勘探规范要求：同一组合内，检波器最大组合高差小于视波长的1/4。即：Δh=V0/(4Fdom)；近年来，李庆忠院士观点：大多数情况下实际起作用的表层速度是降速层速度V1，甚至是高速层速度V2。即：Δh=V1/(4Fdom)，或Δh=V2/(4Fdom)；在很多目的层主频不是很高而次生干扰波非常发育的地区,做到组内时差只要没有超过视周期的1/2就可以得到信噪比较高的低频资料。另外,在处理过程中所做的水平叠加处理还可以进一步校正个别道上的波形失真。因此组合高差计算采用的公式为Δh=V1/(4Fdom)，或Δh=V2/(4Fdom)(Fdom为目的层主频)，这样就会使野外组合高差允许值增加数倍,进而使得垂直测线大距离拉开组合成为可能,压制次生干扰波的能力也会大大增强。而根据西南石油大学尹成教授对渐变地表及突变地表组合高差的理论研究认为：突变地表情况下，最大组合高差限制应为视波长的3/8，而渐变地表情况下，最大组合高差限制则可放大到视波长的3/4。

根据龙门山地区实际情况，需要保护的主频相对较低，仅在30Hz左右，组内时差没有超过视周期的1/2就可以得到信噪比较高的低频资料，试算了工区的实际最大组合高差（表1）：

（1）按李庆忠院士的观点，要保护主频30Hz的有效波，组内高差应控制在25m左右。

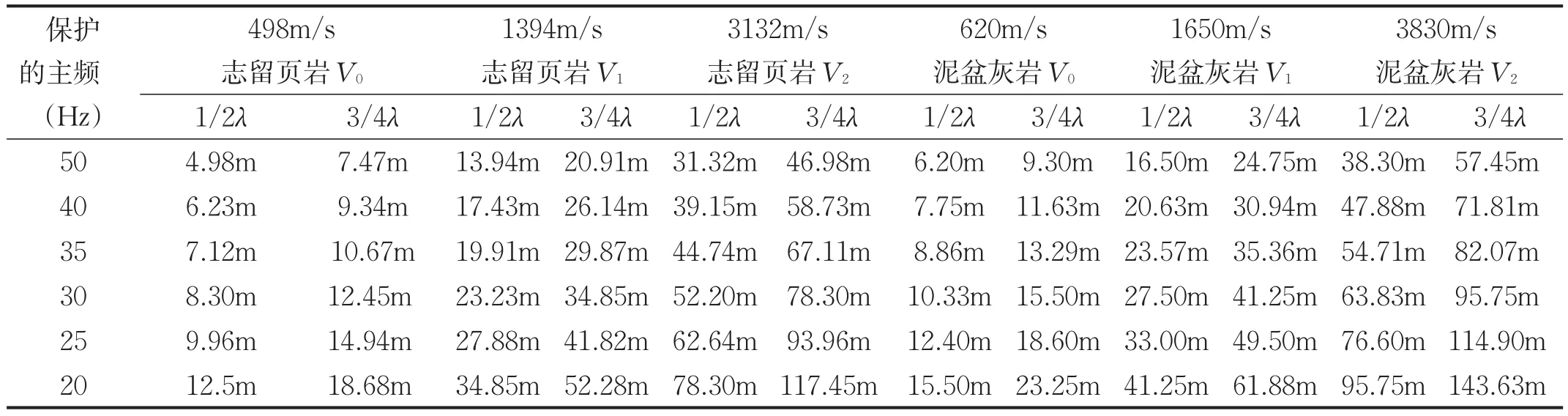
表1 龙门山大山区最大组合高差理论计算一览表

（2）按尹成教授的观点，要保护主频30Hz的有效波，在地表高程渐变区，组内高差应小于40m。

2 理论模型正演记录组合高差分析

基于龙门山近地表实际情况，建立了相应的近地表结构模型，正演模型地表为高程连续变化，从0m逐渐变化到60m，地下为水平层状模型，建立了低速层（V0=600m/s,H0=10m）、降速层（V0=1600m/s,H0=20m）、高速层1（V1=2500m/s,H1=500m）、高速层2（V2=4000m/s,H2=500m）、高速层3（V3=5500m/s,H3=500m）,在正演模型地表布设了组合高差为5m的接收点共计13个，激发点高程为0m。

对理论模型（图1）不同组合高差波形特征进行定性分析认为：最大组合高差限制在25m以下，波形无明显畸变，25m以上不同深度目的层有效反射波形出现了明显畸变（图2）。

3 实际资料组合高差分析

图1 组合高差正演分析理论模型

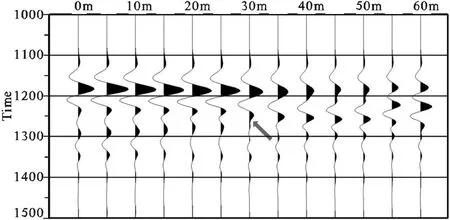
图2 理论模型正演最大组合高差定性分析（T0=1200ms）

选择泥盆系灰岩裸露区进行最大组合高差限制试验。通过野外实际布设的组内高差5m、最大组合高差60m的检波器组合方式进行接收。将试验数据进行室内组合，组成0～60m、组合高差间隔5m记录，进行波形变化的定性分析。通过定性分析认为：从浅至深目的层最大组合高差限制在25m以下，波形保持较好，变化不明显（图3、图4）。

图3 实际测试资料最大组合高差定性分析（1800～2600ms）

4 最大组合高差理论公式适应性分析

根据理论模型及实际资料分析认为：最大组合高差限制在25m以下，波形变化不明显。选取0～25m组合高差记录的固定深度进行频谱分析，获得主频范围，通过统计寻找到固定深度需要保护的主频，反算出最大组合高差限制因素选择条件（表2），并与实际组合高差对比分析认为：

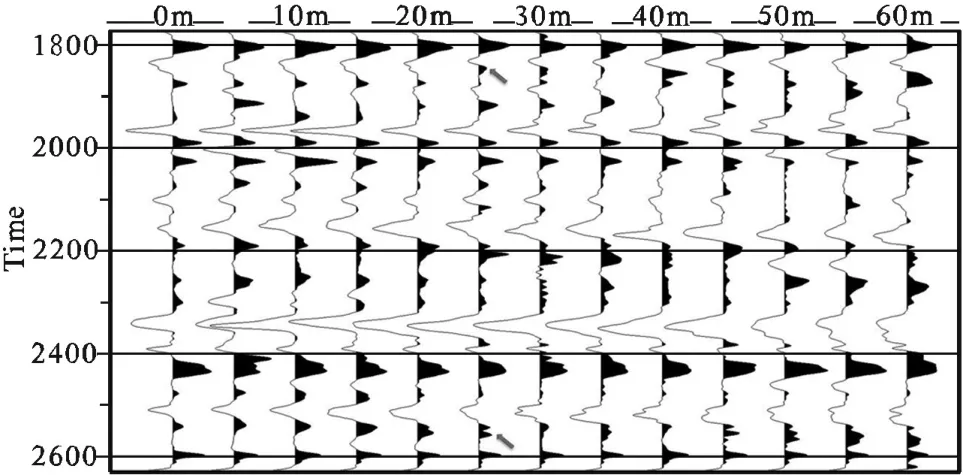
图4 实际测试资料最大组合高差定性分析（3800～4600ms）

（1）龙门山大山区采用降速层速度V1计算最大组合高差与实际情况吻合度较高，低速层速度V0计算出来的最大组合高差限制较实际组合高差小，不利于施工过程中大组合基距的实施，而通过高速层速度V2计算的最大组合高差限制过大，容易导致波形畸变，同时也不利于对高频信号的保护。

（2）按照传统的1/4波长、李庆忠院士提出的1/2波长以及尹成教授提出的3/4波长进行最大组合高差计算认为：传统的1/4波长计算最大组合高差限制较实际情况较小，与龙门山地区组合高差限制实际情况不吻合；而尹成教授提出的3/4波长计算出来的最大组合高差限制较实际资料分析结果明显偏大，过大的组合高差易导致波形畸变、高频信号损失；而李庆忠院士提出的1/2波长计算最大组合高差限制与实际情况较吻合，尤其是针对浅层需要保护的主频相对较高的情况下，实际高差组合分析结果正好落在1/4波长与1/2波长计算结果之间，所以认为：龙门山地区最大组合高差限制采用李庆忠院士提出的1/2波长计算公式较好。

5 应用效果

表2 龙门山地区实际资料反算最大组合高差一览表

结合上述分析，在龙门山地区将检波器组内最大高差放大，控制在25m左右，增加检波器的最大组合基距，获得了信噪比较高的原始记录，同时对剖面成像效果改善明显，尤其是山前隐伏带等重点关注区域构造特征更加明显（图5）。

6 结论与认识

图5 新老资料剖面成像效果对比（上：新资料，下：老资料）

通过理论计算、理论模型的定性分析、组合高差试验资料定性分析、试验资料定量分析、最大组合高差反算后与实际资料再进行对比等方法，获得以下认识：

（1）龙门山双复杂区，重点是提高原始资料信噪比，改善剖面成像效果，所以有效波的低频信息为重点保护对象，检波器大组合基距对有效波不会造成较大伤害。

（2）结合龙门山大山区近地表情况对组合高差限制进行理论计算、对理论模型进行定性分析以及对组合高差试验资料进行分析认为：龙门山大山区最大组合高差限制应控制在25m以内。

（3）根据理论试算及试验资料对比分析结果认为：龙门山地区采用降速层速度V1计算最大组合高差更加合理。

（4）根据最大组合高差定量分析结果认为：龙门山地区采用李庆忠院士提出的1/2波长计算最大组合高差更加合理。

（5）合理检波器组合高差是大山区实施大组合基距检波器接收的基础，更加有利于压制噪音，提高资料信噪比，改善剖面成像效果，落实区域构造特征。

[1]吴希光，李亚林，张孟，等.复杂地区地震资料低信噪比的原因及对策(一)——表层散射波是导致地震资料低信噪比的根本原因[J].天然气工业，2012，32(1):27-30.

[2]吴希光，李志荣，李正佳，等.复杂地区地震资料低信噪比的原因及对策(二)——表层散射波的基本性质及形态特征[J].天然气工业，2012，32(2):38-42.

[3]吴希光，李志荣，张晓斌，等.复杂地区地震资料低信噪比的原因及对策(三)——表层散射波压制的技术方法[J].天然气工业，2012，32(3):57-61.

[4]李庆忠.论地震次生干扰——兼论困难地区地震记录的改进方向[J].石油地球物理勘探，1983，18(3):207-225.

[5]李庆忠.论地震次生干扰(续)——兼论困难地区地震记录的改进方向[J].石油地球物理勘探，1983，18(4):295-314.

[6]罗岐峰，胡杰，张立军，等.柴达木盆地复杂山地组合压噪特性分析[J].青海石油，2013，31(2):7-13.

[7]罗仁泽，黄元溢，曾俊峰，等.宽线大组合地震接收原理及实践[J].天然气技术与经济，2011，5(1):21-23.

[8]吴超，彭更新，雷刚林，等.宽线加大组合地震技术在库车坳陷中部勘探中的应用[J].勘探地球物理进展，2008，31(4):290-295.

[9]李庆忠，魏继东.论检波器横向拉开组合的重要性[J].石油地球物理勘探，2008，43(4):375-382.