KIN SP:A boundary element method based code for single pile kinematic bending in layered soil

Stefano Stacul,Nunziante Squeglia

Department of Civil and Industrial Engineering,University of Pisa,Largo Lucio Lazzarino,Pisa,56122,Italy

1.Introduction

1.1.Literature overview

In seismic areas,piles are commonly designed to resist inertial forces due to the superstructure.Nevertheless,it is important to consider the kinematic effects to properly design pile foundation.

Arise of kinematic interaction phenomena is due to the seismically induced deformations of the soil that interacts with the pile.One of the main important effects of these deformations is the arise of significant strains in soft soil that induce bending moments(kinematic bending moments)on piles.

Pile kinematic response has been studied,among others,by Blaney et al.(1976),Flores-Berrones and Whitman(1982),Kaynia and Kausel(1982),Dobry and O’Rourke(1983),Nogami et al.(1991),Kavvadas and Gazetas(1993),and Tabesh and Poulos(2001).These studies have focused on the motion of the pilehead and only more recently pile bending and curvature have been explored.

Further studies proposed simplified formulations and methods to estimate the maximum kinematic bending moment at the interface of a two-layered soil and/or at the pile-head(Castelli and Maugeri,2009;Dezi et al.,2010;Dobry and O’Rourke,1983;Kavvadas and Gazetas,1993;Maiorano et al.,2009;Mylonakis,2001;Nikolaou et al.,2001;Sica et al.,2011)using beam on dynamic Winkler foundation(BDWF)approaches.

On the other hand,some authors proposed methods able to study the single pile kinematic problem using continuum-based approaches,such as the boundary element method(BEM)(Tabesh and Poulos,2001;Liang et al.,2013),the finite element method(FEM)(Bentley and El Naggar,2000;De Sanctis et al.,2010;Di Laora et al.,2013;Di Laora and Rovithis,2015;Maiorano et al.,2007;Wu and Finn,1997a,b)or procedures based on the stiffness method and dynamic stiffness matrices of layered soils(Cairo and Dente,2007)and hybrid BEM-BDWF approaches(Kampitsis et al.,2013).

Considering the available technical literature about the pile kinematic interaction,it can be outlined that the internal forces generated due to the seismic waves propagation in a pile are affected by the pile-soil relative stiffness(Ep/Es),the pile-head restraint condition(free-head,fixed-head),the thickness and the mechanical properties of the subsoil layers,and the seismic event used as input,while the pile slenderness ratio(L/D,whereLis the length,andDis the diameter)has a minor effect on layered soils with respect to the above aspects.It is well-established that for pile embedded in a layered soil deposit,the bending moment values along the pile-shaft increase at the interface between two adjacent soil-layers with different shear moduli(G)and that the bending moment increment becomes higher as the mechanical impedance increases.More recently,Di Laora et al.(2012)investigated the effect of pile-soil stiffness ratio,interface depth and stiffness contrast in static and transient dynamic conditions on pile bending.In this work,it was found that while the bending strain becomes maximum at resonance,the strain transmissibility function(εp/γ1),relating the peak pile bending strain to soil shear strain at the interface,increases with the excitation frequency.

All the research works on this topic have demonstrated that kinematic bending moments can be responsible for pile damage,especially in the case of high stiffness contrast in a soil deposit profile(Fig.1).

1.2.Simplified design methods

Dobry and O’Rourke(1983)developed a BDWF method that assumes a linear elastic behaviour for the pile and the soil deposit,and the proposed equations are useful to estimate the maximum bending moment at the interface between two layers with different stiffnesses.In this method,it is assumed that the contact between pile and soil is perfect and the soil is subjected to a uniform static stress field.

Nikolaou et al.(2001)on the basis of a parametric study using a BDWF method proposed simplified expressions to evaluate the bending moment at the interface between two soil layers with different stiffnesses in steady-state condition with a frequency approximately equal to the natural frequency of the soil deposit.These expressions are valid when the interface between the two soil layers is located at a depth greater than the pile active length(La).Lacan be estimated using the formulation suggested by Randolph(1981).

Fig.1.Pile-soil system scheme:Free-head pile embedded in a two-layered soil with a high stiffness discontinuity.

One of the weaknesses of the expressions proposed by Nikolaou et al.(2001)is that infinite bending moment is predicted for very slender piles and for layered soils having high stiffness contrast.

Mylonakis(2001)proposed a simplified method for predicting the kinematic bending at the interface of a two-layered soil profile based on response analysis of a mechanistic model.The assumptions are the same as those in Dobry and O’Rourke(1983)method.The improvements are as follows:

(1)The seismic excitation is a harmonic horizontal displacement imposed on the bedrock.

(2)Both the radiation and material damping are considered.

(3)The soil layers are thick,but not unbounded.

The maximum kinematic bending moment is evaluated as

whereEpis the pile elastic modulus,Ipis the area moment of inertia of the pile section,εpis the peak pile bending strain,γ1is the peak shear strain in the upper layer at the interface depth,ris the pile radius,andφis a coefficient that takes into account the effect of frequency.The parameterφcan be considered equal to 1 and in general it is less than 1.25(Mylonakis,2001).

The ratio εp/γ1is a strain transmissibility function(Mylonakis,2001)expressed as

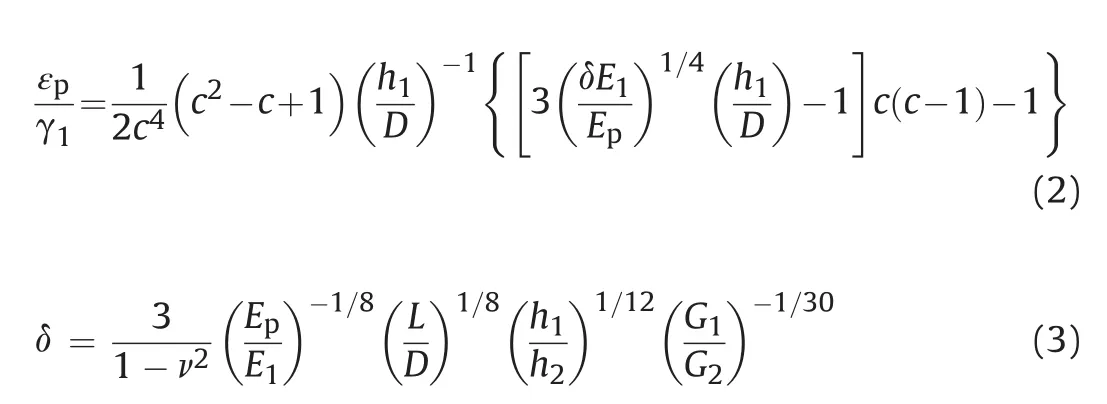
wherecis equal to(G2/G1)1/4;G1,h1andG2,h2are the shear modulus and thickness of the upper and lower soil layer,respectively;Lis the pile length;Dis the pile diameter;andE1is the elastic modulus of the upper layer.

More recently,Di Laora et al.(2012)found that the overall bending moment at the interface can be viewed as the superposition of two counteracting moments:a negative moment that the pile would experience in homogeneous soil having stiffness equal to that of the first layer,and a positive moment due to the restraining action of the increased soil stiffness below the interface.

The possible drawback in Mylonakis expression lies in its difficulty in separating the contributions of the negative and positive mechanisms.

Di Laora et al.(2012)presented a set of harmonic steady-state elastodynamic results obtained by a rigorous finite element analysis and proposed a new semi-analytical formula for evaluating the strain transmissibility function(εp/γ1)(Eq.(4)),and hence the pile bending,at an interface separating two soil layers:

whereχis a regression coefficient that is found to be 0.93.Assumingχclose to unitycanprovide less satisfactory results in the pile bending estimate for shallow interfaces for fixed-head piles,due to the interplay among head and interface moment.

1.3.Pile discretization effect on kinematic analysis

In all the available continuum-based methods(BEM and FEM),the results are sensitive to the element size.Di Laora et al.(2013)observed that the computed bending moments tend to increase with decreasing element size and increasing accuracy.They found that an element size equal to 0.1Dcould provide a satisfactory accuracy.

However,in most of the works mentioned previously,evenif the influence of element size was recognised and a proper sensitivity analysis was performed to select the pile element height able to guarantee the solution accuracy,no general suggestions have been proposed.

For example,in the BEM proposed by Tabesh and Poulos(2001),the analyses refer to a pile with a slenderness ratio(L/D)equal to 20 with a diameterDranging between 0.3 m and 1.5 m,and the element size was kept constant to 0.75 m to compare the results with those obtained by Kavvadas and Gazetas(1993).

In the work of Liang et al.(2013),the pile slenderness ratio was also equal to 20 and it was considered adequate to use 21 pile segments to obtain a good accuracy.However,the above discretization was not adequately justified.Kampitsis et al.(2013)performed the analyses with their hybrid BDWF-BEM model to discretize the column pile with beam elements of 1 m length.

In this work,a computer code(called KIN SP)for the single pile kinematic analysis,based on the BEM,will be presented and validated.Then some results of a parametric study will be discussed,with the aim to suggest the minimum number of boundary elements to guarantee the accuracy of a BEM solution,for typical pilesoil relative stiffness values as a function of the pile diameter,the location of the interface of a two-layered soil profile,and the stiffness contrast.

2.BEM based method for the kinematic analysis of a single pile(KIN SP)

2.1.Model assumptions

The method(computer code KIN SP,Stacul et al.,2017)for the kinematic analysis of a single pile described here is solved using the BEM.The kinematic analysis is preceded by a seismic ground response analysis performed in the time domain with the computer code ONDA(Lo Presti et al.,2006),which provides the soil relative displacements and relative velocities at the centreof eachpile block at each time step.In ONDA,the nonlinear soil behaviour is modelled using the Ramberg-Osgood constitutive law.KIN SP has been completely merged with the code ONDA to provide a standalone analysis tool.The analysis results presented here are limited to the kinematic bending moments.The following model assumptions are made:

(1)The soil deposit has a linear elastic behaviour(the soil nonlinear behaviour is considered in the seismic ground response analysis performed with ONDA).

(2)The soil elastic moduli are equivalent moduli corresponding to the secant moduli at shear strains equal to 65%of the maximum shear strains obtained in the free-field response analysis.

(3)The stresses developed between the pile and the soil are normal to the pile axis.

(4)Each pile block is subjected to a uniform horizontal stress.

(5)The pile is modelled as a thin strip using the Euler-Bernoulli beam theory and is discretized innblocks.

(6)The soil displacement induced by a uniform pressure acting over a pile block is computed by integrating the Mindlin equation(Mindlin,1936).

(7)The equilibrium and the pile-soil displacements compatibility are assumed.

In addition to the above assumptions,the proposed model assumes also that Mindlin solutions are valid both in nonhomogeneous soils and in dynamic conditions.Nevertheless,as stated by Tabesh and Poulos(2001),satisfactory results can be obtained for non-homogeneous soil by assuming in Mindlin equation an average value of soil modulus at the influencing and influenced points.Moreover,the Mindlin equation is not valid for dynamic loading,however,it can be still considered valid if the characteristic wavelength in the soil medium is long compared with the horizontal distance across the zone of higher influence resulting from interaction(Tabesh and Poulos,2001).

2.2.The code KIN SP

A linear elastic behaviour is assumed for the pile.This assumption neglects the actual behaviour of reinforced concrete pile sections such as the development of cracks,the tension stiffening effect and the post-yielding or“inelastic”phase.As observed in Morelli et al.(2017),the influence of tension stiffening becomes higher for reinforced concrete piles with diameters lower than 60 cm and reinforcement ratio lower than 1%.In order to introduce a more advanced constitutive model for reinforced concrete piles with cyclic degradation for dynamic analyses,the model proposed by Andreotti and Lai(2017)may be considered.

The pile flexibility matrix(H)is obtained using the elastic beam theory,and each coefficient of this matrix can be computed using the following equations(Fig.2):

In this way,the incremental horizontal displacements{Δy}of the pile blocks can be obtained:

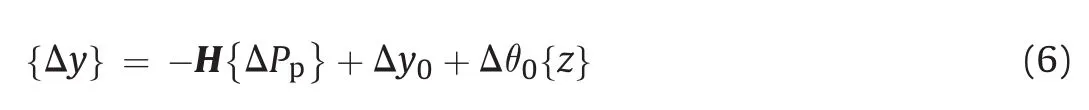
where{ΔPp}is a column vector,containing the incremental loads acting at each pile block,and{ΔPp}={Δp}(tD),where{Δp}is the column vector of the incremental uniform pressures acting on each pile block,tis the height of each pile block,andDis the pile diameter or the pile width;Δy0and Δθ0are the unknown incremental displacement and rotation at the pile-head,respectively;{z}is the column vector containing the depth of the centre of each pile block.

Fig.2.Pile flexibility matrix using the auxiliary restraint method.

The soil flexibility matrix(B)is obtained using the Mindlin solution and each coefficient of this matrix can be calculated using the following equation(Fig.3):

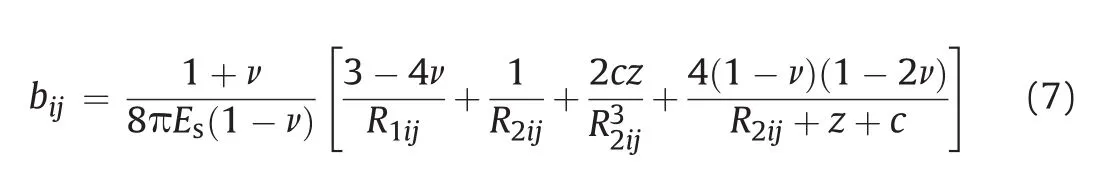
The incremental horizontal displacements{Δs}of the soil can be obtained as

where{ΔPs}is a column vector,containing the incremental loads acting on each pile-soil interface,and{ΔPs}={Δps}(tD),where{Δps}is the column vector of the incremental uniform pressures acting on each pile-soil interface;{Δx}is the column vector of the incremental soil displacements obtained in the ground response analysis using ONDA.

The relationship between{ΔPp}and{ΔPs}is expressed as

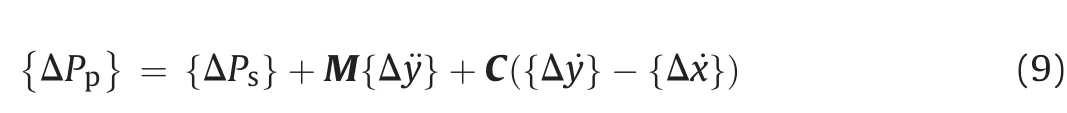
where M is the diagonal mass matrix of the pile;C is the diagonal damping matrix;{Δ¨y}and{Δ˙y}are the column vectors of the incremental accelerations and of the incremental velocities at the pile interface,respectively;{Δ˙x}is the column vector of the incremental soil velocities obtained in the free-field analysis with ONDA.

The elements of the damping matrix are computed using the expression 5ρsVsDtas proposed by Kaynia(1988)for radiation damping in his Winkler method,in whichρsis the soil mass density,andVsis the soil shear wave velocity.The adoption of these coefficients is justified by the fact that they are rather conservative and are also frequency independent(Tabesh and Poulos,2001).

Combining Eq.(9)with Eq.(6)and considering the compatibility between pile and soil incremental displacements,{Δy}={Δs},the following equation is obtained:

Fig.3.Mindlin solution scheme.

This system is solved using the Newmark-βmethod.In this way,the incremental acceleration and the incremental velocity are respectively defined as

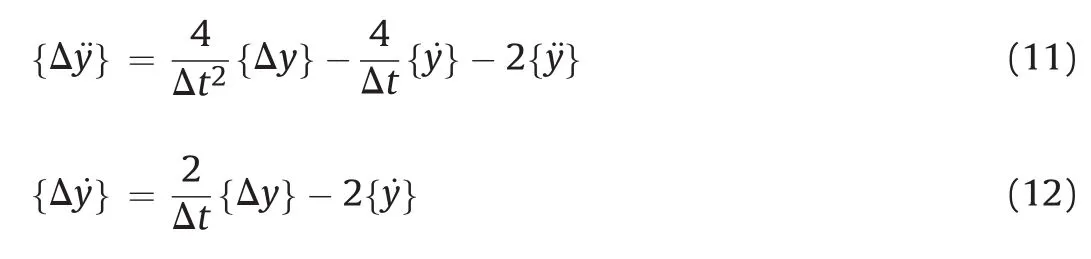
where{˙y}and{¨y}are the column vector of the velocity and of the acceleration at the end of the previous time step,respectively;and Δtis the time step.It is then possible to substitute{Δ¨y}and{Δ˙y}in Eq.(10).The compatibility equations are finally written as

The system defined in Eq.(13)is expressed as function ofn+2 unknowns:nincremental loads acting at each pile-soil interface and the unknown incremental displacement Δy0and rotation Δθ0at the pile-head.The system in Eq.(13)is defined bynequations,and the other two equations required are the translational and rotational equilibrium equations.The system is solved at each time step and the results are plotted in terms of the envelope of the maximum bending moments along the pile shaft.

3.Influence of the pile discretization in BEM based kinematic analysis

As introduced in Section 1.2,the analysis results of BEM based approaches(like KIN SP),in terms of bending moments at the pilehead and at the interface of a two-layered soil,are influenced by many factors including the discretization of the problem domain.Here are presented some results of a parametric study with the aim to suggest the minimum number of boundary elements to guarantee the accuracy of a BEM solution for typical pile-soil relative stiffness values as a function of the pile diameter,the location of the interface of a two-layered soil profile and the stiffness contrast.

The parametric study has been realised on a simplified two layered soil profile(Fig.4),with a total thickness of 30 m and overlying a bedrock with a shear wave velocity equal to 1200 m/s and a unit weight of 22 kN/m3.The soil unit weight and the Poisson’s ratio(ν)for both layers were considered equal to 19 kN/m3and 0.4,respectively,while the shear wave velocities(Vs1andVs2)and the layers thickness(h1andh2)of the upper and lower layers are summarised in Table 1.

The pile had the following properties:the lengthL=20 m,and the elastic modulusEp=25 GPa.The pile-head was fixed,and three pile diameter values were used(D=0.6 m,1 m and 1.5 m).All the kinematic analyses were preceded by a ground response analysis using the computer code ONDA.The acceleration time histories in Figs.5-7 have been applied to the base of the soil deposit model.

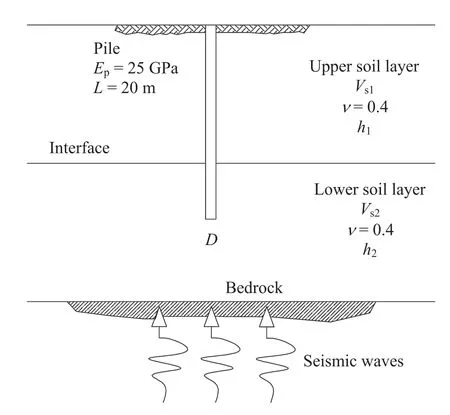
Fig.4.Reference model used for the KIN SP validation.

Table 1Subsoil conditions adopted in the parametric study.

The free-field response was computed in time domain considering linear elastic conditions and a soil damping βsequal to 10%.Each analysis has been repeated,using KIN SP,considering the following number of boundary elements:12,20,40,60,100 and 200.

In Fig.8,for instance,the results obtained with KIN SP are reported in terms of maximum bending moments at the pile-head and at the interface between the two-layered soil for a pile diameter equal to 0.6 m and a stiffness contrastVs2/Vs1equal to 4 using the input motion A-TMZ000.

It is noted that these plots are fitted by hyperbolic curves.This statement can be confirmed in Fig.9,where the same data are plotted using along thex-axis the number of boundary elements(n)and along they-axis the ratio betweennand the computed moment(M).

This fact permits to evaluate,for each analysis case,the coefficientsaandbof the hyperbolic law rewritten in the following terms:

The value assumed by 1/brepresents a limit value of the maximum bending moment(Mlim)related with a specific analysis case(Fig.8)for a number of boundary elements that tends to infinity.TheMlimhas not been considered as an exact solution but rather as a limit value for the maximum bending moment.Finally,the following expression was adopted to provide an estimate of the analysis result errors due to the discretization:

Figs.10 and 11 plot some results of the parametric study,representing the error(defined in Eq.(15))in the estimation of the bending moments at the pile-head and at the interface of the two layered soil using the input motion A-TMZ000.

Observing the parametric analysis results,the following remarks can be drawn:

(1)The analysis error decreases with increasing pile diameter.

(2)The error is larger for higher stiffness contrast.

(3)The error in the evaluation of the maximum bending moments is lower when the interface between the two layers is located at higher depth.

(4)In general,for typical pile diameters and pile-soil relative stiffness,a boundary element size lower than 0.33D(in m)can guarantee an error less than 10%in the evaluation of the maximum bending moments at the pile-head and at the interface of the two-layered soil.

4.Validation of KIN SP

Fig.5.Acceleration time history(left)and Fourier spectrum(right),A-TMZ000(scaled at 0.35 g).

Fig.6.Acceleration time history(left)and Fourier spectrum(right),A-STU270(scaled at 0.35 g).

Fig.7.Acceleration time history(left)and Fourier spectrum(right),E-NCB090(scaled at 0.35 g).

Fig.8.Computed maximum kinematic bending moments as a function of the number of boundary elements.

Fig.9.Relationship between n/M and n for the data presented in Fig.8.

Fig.10.Error vs.number of boundary elements with varying stiffness contrast(Vs2/Vs1).

The validation has been realised by comparing the KIN SP kinematic analysis results in terms of maximum bending moment with those computed using the simplified expressions suggested by Mylonakis(2001)and Di Laora et al.(2012)and in terms of bending moment envelope with those obtained by Aversa et al.(2009)using the quasi-three-dimensional(3D)finite element code VERSAT-P3D(Wu,2006).The VERSAT-P3D numerical model is able as KIN SP to obtain results considering a linear or a nonlinear soil response.

Piles are modelled using the ordinary Eulerian beam theory.Bending of the piles occurs only in the direction of shaking.Dynamic soil-pile interaction is maintained by enforcing displacement compatibility between the pile and soils.An eight-node brick element is used to represent the soil and an eight-node beam is used to simulate the piles.Direct step-by-step integration using the Wilson-θmethod is employed in VERSAT-P3D to solve the equations of motion.

An equivalent linear method is employed in VERSAT-P3D to model the nonlinear hysteretic behaviour of soil.The hysteretic behaviour of soil is approximated by a set of secant shear moduli and viscous damping ratios compatible with current levels of shear strain.To approximate the nonlinear behaviour of soil,the compatibility among the secant shear modulus,damping ratio,and shear strain is enforced at each time step during the integration of equations of motions.The VERSAT-P3D analysis results shown here have been obtained updating the shear moduli and damping ratios every 0.5 s based on the peak strain levels from the previous time interval(Maiorano et al.,2007).The damping is essentially of the Rayleigh type,which is both mass and stiffness dependent.The hysteretic damping ratio is prescribed as a function of element shear strain.

All the simulations were performed considering a simplified soil deposit described in the following section,using the same acceleration time histories selected on the Italian accelerometric archive.The results obtained with KIN SP were realised considering 100 boundary elements on the basis of the parametric study presented in the Section 3.

4.1.Reference soil deposit and pile properties for linear analyses

The validation of the computer code KIN SP has been realised on a simplified two-layered soil profile with a total thickness of 30 m and overlying a bedrock with a shear wave velocity of 1200 m/s and a unit weight of 22 kN/m3(see Fig.4).The shear wave velocities of the upper(Vs1)and lower(Vs2)soil layers were those indicated in Table 1,while the soil unit weight and the Poisson’s ratio(ν)for both layers were considered equal to 19 kN/m3and 0.4,respectively.

The pile had the following properties:the diameterD=0.6 m,1 m and 1.5 m;the lengthL=20 m;and the elastic modulusEp=25 GPa.The pile-head has been considered fixed against the rotation.

4.2.Linear analysis results

A preliminary ground response analysis was performed using the code ONDA.The acceleration time histories used in this work(identified by the codes A-TMZ000,A-STU270,and E-NCB090)have been selected from the database ITACA(Luzi et al.,2016),and the motions have been scaled to values ofarequal to 0.35 g(Figs.5-7)and applied to the base of the soil deposit model.

The free-field response was computed in time domain considering linear elastic conditions and a soil dampingβsequal to 10%.The analysis results have been compared(Figs.12-14),in terms of maximum bending moment at the interface(Mint),with those obtained using the expressions suggested by Mylonakis(2001)and Di Laora et al.(2012).

Fig.11.Error vs.number of boundary elements with varying pile diameter(D).

In each subfigure of Figs.12-14,a total of 27 cases(3 pile diameters,3 stiffness contrasts and 3 interface depths)have been reported.The dotted lines represent a variation of±20%with respect to the continuous line.For all input motions,it can be noted that the KIN SP bending moments at the interface overestimate the values calculated using the solution proposed by Mylonakis(2001)and slightly underestimate those obtained with the formulation by Di Laora et al.(2012).

Using the Mylonakis formulation(Eq.(1)),the coefficient φhas been evaluated by taking into account the strain transmissibility dependency on frequency as described in Mylonakis(2001).The differences between KIN SP and Mylonakis solutions can be justified by the fact that the latter has been deduced considering harmonic excitations and not real seismic motions.

The KIN SP analysis results have been compared also in terms of bending envelope with those obtained by Aversa et al.(2009)using the quasi-3D finite element computer programme VERSAT-P3D.As shown in Figs.15-17,a good agreement can be observed between the results computed using these two different methods.

In general,the bending envelope of VERSAT-P3D is well reproduced by KIN SP results,however,the maximum bending at the interface is underestimated by an average of 19%.These differences could be related to the different pile modelling and discretization adopted.Moreover,in KIN SP,the free-field and the kinematic interaction analyses are uncoupled,whereas in VERSAT-P3D,,the pile-soil interaction problem is coupled with the ground response analysis.

Figs.15-17 also show the maximum bending moment at the interface computed using the solutions proposed by Mylonakis(2001)and Di Laora et al.(2012).

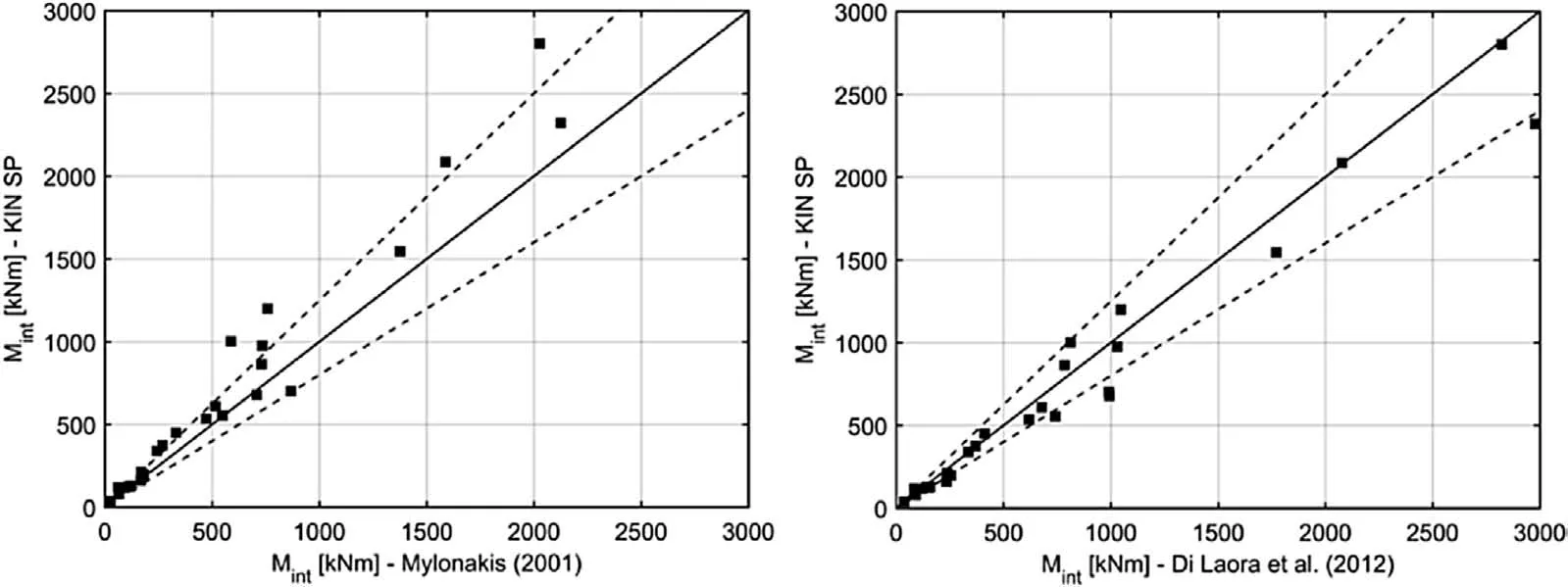
Fig.12.Comparison between KIN SP and simplified expressions(Mylonakis,2001;Di Laora et al.,2012).Input motion:E-NCB090.

Fig.13.Comparison between KIN SP and simplified expressions(Mylonakis,2001;Di Laora et al.,2012).Input motion:A-STU270.

Fig.14.Comparison between KIN SP and simplified expressions(Mylonakis,2001;Di Laora et al.,2012).Input motion:A-TMZ000.

4.3.Reference soil deposit and pile properties for nonlinear analyses

The nonlinear analyses with KIN SP have been realised on a simplified two-layered soil profile with a total thickness of 30 m and overlying a bedrock with a shear wave velocity equal to 1200 m/s and a unit weight of 22 kN/m3.The shear wave velocities of the upper layer(Vs1)are equal to 100 m/s and 150 m/s,while the lower layer has aVs2equal to 400 m/s.The interface of the two soil layers is located at a depth of 15 m.The two resulting profiles can be classified as subsoil types D and C,respectively,according to EN 1998-1(2005)on the basis of the parameterVs,30,which is the average shear wave velocity of the first 30 m in depth.The soil unit weight and the Poisson’s ratio(ν)for both layers were considered equal to 19 kN/m3and 0.4,respectively.

Fig.15.Comparison between KIN SP and VERSAT-P3D results(input motion:ATMZ000).

Fig.16.Comparison between KIN SP and VERSAT-P3D results(input motion:ASTU270).

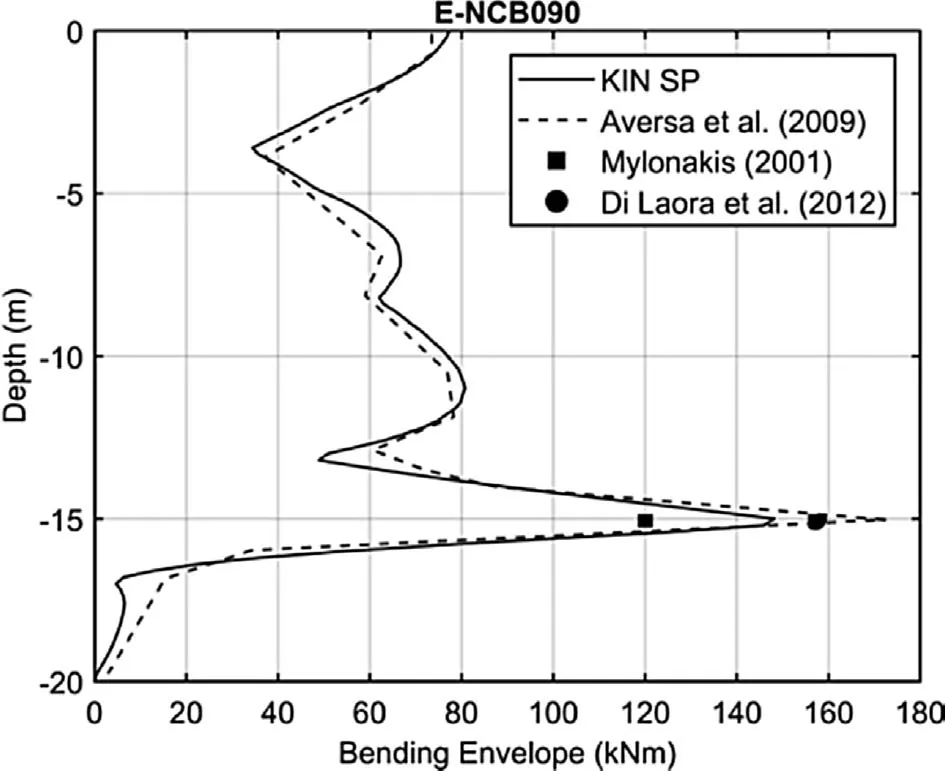
Fig.17.Comparison between KIN SP and VERSAT-P3D results(input motion:ENCB090).

The pile had the following properties:the diameterD=0.6 m,the lengthL=20 m,and the elastic modulusEp=30 GPa.The pilehead has been considered fixed against the rotation.Nonlinear analyses are carried out employing the soil data provided by Maiorano et al.(2007),which are shown in Fig.18 in terms ofGs/G0-γcurves.On the basis of these data,the parametersαandRof the Ramberg-Osgood model are obtained under the assumption that the reference strainγrefis 0.5%for the upper layer of soft clay and 0.067%for the lower layer of gravel.Specifically,values ofα=19.89 andR=2.33 are determined for the clay,andα=17.11 andR=2.09 for the gravel(Cairo et al.,2008).The reference strainγrefis defined as the ratio of the maximum soil shear resistance(τmax)to the shear modulus at small strain level(G0).The modulus reduction curve,using the Ramberg-Osgood model,is defined as

whereGsis the secant shear modulus.

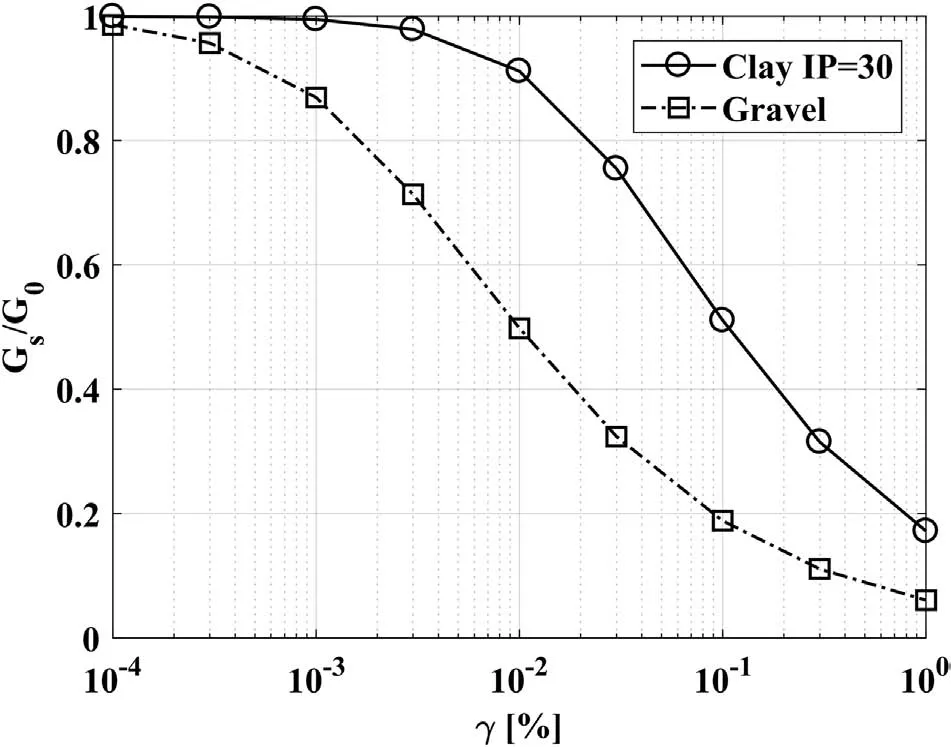
Fig.18.Shear modulus reduction curves used in the analyses.IP represents the plasticity index.

Fig.19.Comparison between KIN SP and VERSAT-P3D nonlinear analysis results(input motion:A-TMZ000)for subsoil type C.

4.4.Nonlinear analysis results

The acceleration time histories used in this work(identified by the codes A-TMZ000 and A-STU270)have been selected from the database ITACA(Luzi et al.,2016),and the motions have been scaled to values ofarequal to 0.35g(Figs.5 and 6)and applied to the base of the soil deposit model.

The KIN SP analysis results have been compared in terms of bending envelope with those obtained by Maiorano et al.(2007)using the quasi-3D finite element computer programme VERSATP3D(Figs.19-21).

As in the case of linear analyses,the bending envelope of VERSAT-P3D is well reproduced by KIN SP results.Figs.19 and 20 report the analysis results related with the input motion ATMZ000.In these cases,it can be observed that computed values of bending moments are in good agreement with those of VERSATP3D both at the interface and along the entire pile length.As shown in Fig.21,the results referring tothe input motion A-STU270 are qualitatively in agreement but not quantitatively.KIN SP overestimates the whole bending profile.These differences can be related to the different frequency contents of these two acceleration time histories(Figs.5 and 6)and to the approximated modelling of the nonlinear soil behaviour in VERSAT-P3D,in which the shear moduli and damping ratios are updated every 0.5 s(i.e.approximately every 50 or 100 points of the time history data,according to the sampling rate).

Fig.20.Comparison between KIN SP and VERSAT-P3D nonlinear analysis results(input motion:A-TMZ000)for subsoil type D.

Fig.21.Comparison between KIN SP and VERSAT-P3D nonlinear analysis results(input motion:A-STU270)for subsoil type C.

5.Conclusions

In this work,a BEM based computer code(called KIN SP)was presented,which is able to analyse the single pile kinematic problem.In the first section,the attention was focused on the influence of discretization on BEM analysis results,in terms of bending moments at the pile-head and at the interface of a two layered soil.

A parametric study was carried out using the developed code KIN SP,with the aim to suggest the minimum number of boundary elements to guarantee the accuracy of a kinematic analysis using BEM.

The parametric analyses suggest that for typical pile diameters and pile-soil relative stiffness,a boundary element size lower than 0.33Dcan guarantee a reasonable error in the evaluation of the maximum bending moments.Based on the parametric study shown here,it is outlined that the results obtained using BEM and that presented on previously developed works can be affected by an underestimation of the maximum bending moments at the pilehead and at the interface of a two-layered soil ranging between 20%and 50%if the typical discretization with 21 elements was considered.

The proposed method was then validated considering both a linear and a nonlinear soil response.In the first case,the KIN SP results,in terms of bending envelope and maximum bending moment at the interface of a two-layered soil,have been compared with those obtained by simplified formulations(Mylonakis,2001;Di Laora et al.,2012)and a quasi-3D FEM code(VERSAT-P3D).In the second case,the comparison has been carried out only with the solutions by nonlinear FEM analyses.For the pile-soil configurations and input motions considered in the linear analyses,KIN SP overestimates the bending moment values obtained using the solution proposed by Mylonakis(2001),probably because the latter has been deduced considering harmonic excitations and not real seismic motions,while slightly underestimates those obtained with the formulation by Di Laora et al.(2012).

In the case of linear analyses,the bending envelope of VERSATP3D is well produced by KIN SP and the differences in the maximum bending moments could be related to the different pile modelling and discretization adopted.

In the case of nonlinear analyses,the agreement with VERSATP3D results is good,however,some differences were noted for a specific acceleration time history.These differences may be due to the frequency content of the input motion and to the approximated modelling of the nonlinear soil behaviour in VERSAT-P3D.

Conflicts of interest

The authors wish to confirm that there are no known conflicts of interest associated with this publication and there has been no significant financial support for this work that could have influenced its outcome.

Andreotti G,Lai CG.A nonlinear constitutive model for beam elements with cyclic degradation and damage assessment for advanced dynamic analyses of geotechnical problems.Part I:theoretical formulation.Bulletin of Earthquake Engineering 2017;15(7):2785-801.

Aversa S,de Sanctis L,Maiorano RMS.Approccio semplificato per la valutazione dei momenti di interazione cinematica nei pali di fondazione sotto azioni sismiche.In:XIII Convegno ANIDIS.Bologna:Associazione Nazionale Italiana Di Ingegneria Sismica;2009(in Italian).

Bentley KJ,El Naggar MH.Numerical analysis of kinematic response of single piles.Canadian Geotechnical Journal 2000;37(6):1368-82.

Blaney GW,Kausel E,Roesset JM.Dynamic stiffness of piles.In:Proceedings of the 2nd International conference on numerical methods in geomechanics,vol.2.New York:American Society of Civil Engineers;1976.p.1010-2.

Cairo R,Dente G.Kinematic interaction analysis of piles in layered soils.In:Proceedings of the 14th European conference on soil mechanics and geotechnical engineering.IOS Press;2007.

Cairo R,Conte E,Dente G.Nonlinear seismic response of single piles.In:Santini A,Moraci N,editors.2008 Seismic Engineering conference commemorating the 1908 Messina and Reggio Calabria earthquake.American Institute of Physics;2008.p.602-9.

Castelli F,Maugeri M.Simplified approach for the seismic response of a pile foundation.Journal of Geotechnical and Geoenvironmental Engineering 2009;135(10):1440-51.

De Sanctis L,Maiorano R,Aversa S.A method for assessing kinematic bending moments at the pile head.Earthquake Engineering&Structural Dynamics 2010;39(10):1133-54.

Dezi F,Carbonari S,Leoni G.Kinematic bending moments in pile foundations.Soil Dynamics and Earthquake Engineering 2010;30(3):119-32.

Di Laora R,Rovithis E.Kinematic bending of fixed-head piles in nonhomogeneous soil.Journal of Geotechnical and Geoenvironmental Engineering 2015;141(4).https://doi.org/10.1061/(ASCE)GT.1943-5606.0001270.

Di Laora R,Mandolini A,Mylonakis G.Insight on kinematic bending of flexible piles in layered soil.Soil Dynamics and Earthquake Engineering 2012;43:309-22.

Di Laora R,Mylonakis G,Mandolini A.Pile-head kinematic bending in layered soil.Earthquake Engineering&Structural Dynamics 2013;42(3):319-37.

Dobry R,O’Rourke MJ.Discussion of“Seismic response of end-bearing piles”by Raul Flores-Berrones and Robert V.Whitman(April,1982).Journal of Geotechnical Engineering 1983;109(5):778-81.

EN 1998-1.Eurocode 8:design of structures for earthquake resistance-part 1:general rules,seismic actions and rules for buildings.British Standards Institution;2005.

Flores-Berrones R,Whitman RV.Seismic response of end-bearing piles.Journal of the Geotechnical Engineering Division,ASCE 1982;108(4):554-69.

Kampitsis AE,Sapountzakis EJ,Giannakos SK,Gerolymos NA.Seismic soil-pilestructure kinematic and inertial interaction-a new beam approach.Soil Dynamics and Earthquake Engineering 2013;55:211-24.

Kavvadas M,Gazetas G.Kinematic seismic response and bending of free-head piles in layered soil.Geotechnique 1993;43(2):207-22.

Kaynia AM.Dynamic interaction of single piles under lateral and seismic loads.Esteghlal Journal of Engineering 1988;6:5-26(in Persian).

Kaynia AM,Kausel E.Dynamic stiffness and seismic response of pile groups.Research report R82-03.University of Western Ontario,Massachussets Institute of Technology;1982.

Liang F,Chen H,Guo WD.Simplified boundary element method for kinematic response of single piles in two-layer soil.Journal of Applied Mathematics 2013.https://doi.org/10.1155/2013/241482.

Lo Presti DC,Lai C,Puci I.ONDA:computer code for nonlinear seismic response analyses of soil deposits.Journal of Geotechnical and Geoenvironmental Engineering 2006;132(2):223-36.

Luzi L,Pacor F,Puglia R.Italian Accelerometric Archive version 2.1.Istituto Nazionale di Geofisica e Vulcanologia,Dipartimento della Protezione Civile Nazionale.2016.https://doi.org/10.13127/ITACA/2.1.

Maiorano RMS,Aversa S,Wu G.Effects of soil non-linearity on bending moments in piles due to seismic kinematic interaction.In:Proceedings of the 4th International conference on earthquake geotechnical engineering. Thessaloniki,Greece;2007.p.25-8.

Maiorano RMS,de Sanctis L,Aversa S,Mandolini A.Kinematic response analysis of piled foundations under seismic excitation.Canadian Geotechnical Journal 2009;46(5):571-84.

Mindlin RD.Force at a point in the interior of a semi-infinite solid.Physics 1936;7(5):195-202.

Morelli F,Amico C,Salvatore W,Squeglia N,Stacul S.Influence of tension stiffening on the flexural stiffness of reinforced concrete circular sections.Materials 2017;10(6):669.

Mylonakis G.Simplified model for seismic pile bending at soil layer interfaces.Soils and Foundations 2001;41(4):47-58.

Nikolaou S,Mylonakis G,Gazetas G,Tazoh T.Kinematic pile bending during earthquakes:analysis and fields measurements.Geotechnique 2001;51(5):425-40.

Nogami T,Jones HW,Mosher RL.Seismic response analysis of pile-supported structure:assessment of commonly used approximations. In:Proceedings of the 2nd International conferences on recent advances in geotechnical earthquake engineering and soil dynamics.University of Missouri-Rolla;1991.p.931-40.

Randolph MF.The response of flexible piles to lateral loading.Geotechnique 1981;31(2):247-59.

Sica S,Mylonakis G,Simonelli AL.Transient kinematic pile bending in two-layer soil.Soil Dynamics and Earthquake Engineering 2011;31(7):891-905.

Stacul S,Lo Presti D,Squeglia N.KIN SP 1.0(KINematic interaction analysis of Single Pile):user’smanualversion 1.0.2017.https://doi.org/10.13140/RG.2.2.15632.61444.

Tabesh A,Poulos H.Pseudostatic approach for seismic analysis of single piles.Journal of Geotechnical and Geoenvironmental Engineering 2001;127(9):757-65.

Wu G.VERSAT-P3D version 2006:quasi-3D dynamic finite element analysis of single piles and pile groups.Wutec Geotechnical International Canada;2006.

Wu G,Finn WDL.Dynamic elastic analysis of pile foundations using finite element method in the frequency domain.Canadian Geotechnical Journal 1997a;34(1):34-43.

Wu G,Finn WDL.Dynamic nonlinear analysis of pile foundations using finite element method in the time domain. Canadian Geotechnical Journal 1997b;34(1):44-52.