Influence of loading and heating processes on elastic and geomechanical properties of eclogites and granulites

Hem Bahadur Motra,Sascha Zertani

aDepartment of Geosciences,Marine and Land Geomechanics and Geotechnics,University of Kiel,Ludewig-Meyn-Str.10,Kiel,24118,Germany

bInstitut für Geologische Wissenschaften,Freie Universität Berlin,Malteserstr.74-100,Berlin,D-12249,Germany

1.Introduction

Reliable estimates of the elastic and geomechanical characteristics of natural rocks are required for almost any form of design and analysis used in various geomechanical projects such as mining,nuclear waste disposal,geothermal energy,and geotechnical engineering(Ringwood, 1985;Gibb,1999; Sanchez et al.,2012;Feng et al.,2012;Nakaten et al.,2014).Changes in loading and temperature play an important role in the behavior and stability of engineering structures built on or within crystalline rocks in terms of the integrity of the elastic and geomechanical properties,for example by inducing the closing or further opening of existing cracks as well as the generation of new cracks.Although many geomechanical projects are planned and executed within metamorphic basement rocks(Watts et al.,1993;Carpenter,1997),the elastic and geomechanical properties of such rocks remain poorly constrained compared to those of sedimentary rocks.Additionally,while rock deformation and failure or strength behavior are fundamental problems in geomechanics(Schön,2011),most previous studies have focused on the effect of uniaxial compression on the properties of various rock types,establishing that changes in loading and heating modify the elastic and geomechanical properties of rocks including elastic moduli,e.g.shear modulus,bulk modulus and Poisson’s ratio as well as compressive and tensile strengths(e.g.Cheatham,1968;Wai et al.,1982;Heuze,1983;Inada and Yorkota,1984;Alm et al.,1985;Hommand-Etienne and Houpert,1989;Duclos and Paquet,1991).

Experimentalstudies(Griggsetal.,1960;Scholz,1968;Tapponnier and Brace,1976;Simmons and Cooper,1978;Handin and Carter,1979;Batzle et al.,1980;Bauer et al.,1981;Fredrich and Wong,1986)dealing with the physical properties of natural rocks have shown that high loading and thermal stress can lead to volume changes of the rock forming minerals as well as various changes in mineralogy and microstructures(Merriam et al.,1970;Sammis and Ashby,1986;Ashby and Sammis,1990;Prikryl,2001)and thus induce changes in rock elasticity and geomechanical properties(Rocchi et al.,2003,2004;Balme et al.,2004;Spieler et al.,2004;Vinciguerra et al.,2005;Smith et al.,2005;Kueppers et al.,2006;Lavalle et al.,2007,2008;Benson et al.,2008;Scheu et al.,2008;Cordonnier et al.,2009;Heap et al.,2009,2010,2014;Loaiza et al.,2012;Kendrick et al.,2013a,2013b).

Seismic wave velocities(compressional P-wave(Vp)and shear S-wave(Vs)),which are closely linked to the elastic and geomechanical properties,can be determined using the ultrasonic pulse emission technique(Kern et al.,1997).Properties that influence the velocity of seismic waves traveling through a rock include mineral assemblage and orientation(anisotropy),density,porosity,pore filling and alteration(Lama and Vutukuri,1978),all in dependence of confining pressure and temperature.Although,previous studies have dealt with the pressure dependence of ultrasonic wave velocities in rocks(e.g.D’Andrea et al.,1966;Deere and Miller,1966;Smorodinov et al.,1970;Youash,1970;Kern,1978;Gebrande et al.,1982;Kern et al.,1997,2001;Punturo et al.,2005;Moradian and Behnia,2009;Sarkar et al.,2012),few experiments have focused on the temperature dependence(e.g.Kern et al.,1997).Motra and Wuttke(2016)and Wuttke et al.(2017)studied the characteristics of acoustic emissions during the deformation of different kinds of metamorphic rocks under true in situ conditions.They suggested that rock fabric has an important effect on the spatial and temporal distribution of microfractures.However,many aspects of the impact of mechanical loading and thermal stress on the true triaxial conditions of metamorphic rocks are not well understood.This includes the effects of grain distribution and microcracking as well as the influence of loading and heating rates on the rocks geomechanical properties and the different impacts when comparing uniaxial and true triaxial conditions.

Many in situ stress and heating processes are relevant for engineering applications.For example,heat generated from radioactive waste repositoriescauses a long-term increase in the temperature of the host rock.Unfortunately,little is known regarding how thermal stress influences the mechanical properties of the rock.

In this context,we focus on the characterization of elastic properties of metamorphic rocks and addresses the influence of pressure and temperature changes.For this,mechanical and temperature stress tests were performed on granulite and eclogite samples at various confining pressures(up to 600 MPa)and temperatures(up to 600°C),and elastic wave velocities were measured under true triaxial conditions.The acoustic emissions recorded during the experiments were then used to calculate geomechanical properties.

2.Theoretical background

The propagation of an elastic wave through an elastic medium can be described by the infinitesimally small deformations in the transmitting body as a response to an external stress.Hooke’s law states that for small elastic deformations,the strain that a deformed body experiences is linearly proportional to the applied stress.This can be expressed mathematically as

whereσis the second-rank stresstensor,C represents a fourth-rank tensor of elastic stiffness(i,j,k,l=1,2,3,indicating one of the three orthogonal axes)with 81 components,and ε is a second rank strain tensor:

where u is the displacement.Eq.(1)can be further reduced from four indices(i,j,kandl)to two indices(mandn)by introducing the’Voigt’notation(Nye,1985)and considering the conservation of energy:

Then the generalized Hooke’s law can be simplified into a matrix equation:

The elastic stiffness tensor can be reduced from 81 to 36 independent components or elastic constants.EachCijis one of the components of a 6 6 symmetric matrix with the stiffness tensor reduced to 21 independent components that is symmetric about the diagonal:

This describes the stress-strain relations for a general anisotropic material such as that observed in a triclinic symmetry in which the indicesIandJare related toijaccording to the cyclical notationI,J=1,2,3,4,5,6 whenijorkl=11,22,33,13 or 31,23 or 32,12 or 21,respectively.

For an isotropic material,the number of independent constants reduces to two,and the tensor of elasticity has the form:

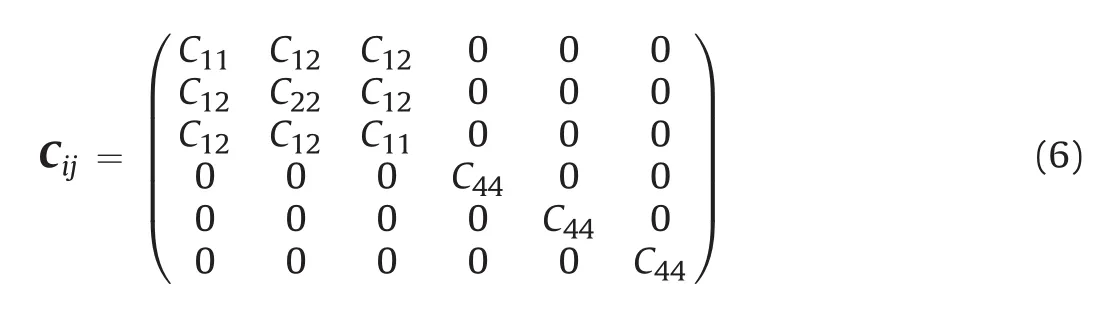
withC12=C11-2C44.The relationship between the components and the Lamé parametersλandμis

whereρis the bulk density.

In addition to the Lamé parametersλand μ,any pair of two of the following moduli can be used to describe the elastic properties of an isotropic material.

However,if the mean elastic wave velocities inx,y,zdirection(VpandVs,respectively)and bulk densityρare known from measurements,the elastic parameters can be calculated:

The dry density(ρ)is determined as follows:

wheremdis the weight of the sample after drying andVis the sample volume.The Poisson’s ratio νis calculated using

and the bulk compressional modulusKis calculated as follows:

3.Sample characterization

The samples analyzed in this study are natural metamorphic rocks(eclogites and granulites)and were collected in Norway.They represent surface samples of crystalline basement rocks.In total,four samples were investigated.

Samples A and B are eclogites and dominantly contain clinopyroxene(omphacite),garnet,clinozoisite,kyanite and mica.While sample A(Fig.1a)represents an unaltered eclogite,sample B(Fig.1b)shows clear signs of retrogression in the amphibolite-facies(symplectites).Both samples have a pronounced foliation dominantly produced by the shape preferred orientation(SPO)of omphacite,kyanite,and clinozoisite.The rocks lineation is clearly visible macroscopically and is produced by stretched mineral grains(e.g.clinopyroxene)and stretched mineral aggregates.

Samples C1 and C2 are aliquots of the same granulite sample(Fig.1c).Both contain abundant plagioclase together with garnet and clinopyroxene(diopside).Sample C2 contains a higher amount of clinopyroxene and garnet in comparison to sample C1.Additionally,microscopic zoisite needles in both samples indicateminor rehydration of the rocks.The foliation seen in samples C1 and C2 is less pronounced than that in samples A and B and is mainly produced by aligned garnets and/or clinopyroxene.The lineation is produced by the elongated aggregates of garnet and clinopyroxene.

Although the mineral composition of the sample selectedfor the experiments varies(Fig.1),they comprise very similar elemental compositions as obtained by X-ray fluorescence(XRF)analysis(Table 1).

4.Experimental setup

The elastic P-and S-wave velocities(VpandVs)and the resulting velocity anisotropies of the investigated samples were determined experimentally using the ultrasonic pulse emission technique(Lama and Vutukuri,1978;Rummel and Van Heerden,1978;ISRM,2007).The measurements were conducted on cube-shaped specimens(Fig.2)in a true triaxial multianvil press,which allows maximum pressure and temperature conditions of 600 MPa and 600°C,respectively.A state of nearly isotropic stress was achieved by confining the sample cube with six pyramidal pistons.The arrangement of the sample-piston-transducer assembly allows simultaneous measurements ofVpand the two orthogonally polarized shear wave velocities(Vs1,Vs2),each in three orthogonal directions of a sample cube(43 mm edge-length).The possibility to measureVs1andVs2allows for the extraction of the amplitude of shear wave splitting,which in itself is a measure for anisotropy(Kern et al.,1997,2001;Punturo et al.,2005;Scheu et al.,2006).

Fig.1.Microscope images depicting the main rock forming minerals of samples A(a)and B(b)as well as C1 and C2(c).The images depict the xz-plane of the samples with x being horizontal and z vertical in each image.cpx-clinopyroxene;grt-garnet;symp-symplectites;plg-plagioclase.

Measurements were carried out over a range of pressures up to 600 MPa and temperatures up to 600°C.The measurement procedure can be divided into three cycles.During the first cycle(pressure cycle),pressure is increased stepwise,starting with 12 MPa followed by 25 MPa,35 MPa,50 MPa,75 MPa and 100 MPa.Following that,the applied pressure is increased in steps of 50 MPa up to a maximum of 600 MPa.The sample is then depressurized using the same increments as during pressurization.The temperature during this cycle remains at 20°C.

During the second cycle(pressure and temperature cycle),pressure and temperature are increased stepwise with increments of 100 MPa and 100°C,respectively,until the maximum conditionsof 600 MPa and 600°C are reached.The last cycle(release path)involves the decrease of temperature in steps of 100°C while maintaining the maximum pressure of 600 MPa.After the temperature is released completely, the pressure is decreased in increments of 50 MPa.At every step of the described three cycles,P-and S-wave velocitites are measured to ensure that the influences of pressure and temperature can be analyzed independently.The heating rate during the experiments is approximately 100°C/30 min and it is necessary to maintain the temperature for 30 min in order to guarantee that all of the sample cube has a homogeneous temperature.

Table 1Major element compositions of the investigated samples(in weight%;b.d.l=below detection limit).

Fig.2.Representative illustration of a cube-shaped sample and its sample reference system as used during the experiments.x is parallel to the rocks lineation and z is perpendicular to the foliation(xy plane).

To measure the directional dependence of wave velocities(anisotropy),particularly in natural metamorphic rocks,which are generally anisotropic,the three orthogonal measuring directions must be related to the structural reference framex,y,z,wherezis perpendicular andxandyare parallel to the foliation(xyplane).Further,xis parallel to the samples lineation(Fig.2).Length changes(volume changes)of the samples as a function of pressure and temperature were obtained by measuring the piston displacements.A complete set of measured data comprises three P-wave velocities and six S-wave velocities obtained by determining the time it takes thewave to travel through the sample cube and the cubes changes in length(volume changes).The sample-piston-transducer assembly is identical to the assembly used in Kern et al.(1997)and the transducers operate at 2 MHz(P-wave)and 1 MHz(S-wave).

5.Results

5.1.Seismic wave velocities and anisotropy

P-wave velocities(Vp)for all samples increase with pressure,regardless of their propagation direction with respect to the structural reference frame of the sample.In the lower pressure range(up to approximately 200-250 MPa),the increase is rapid and non-linear.When further increasing pressure,the increase inVpis slight and linear in a first approximation.The results obtained for S-wave velocities show the same qualitative trend.Seismic velocity increase with increasing pressure is a well-known behavior of natural rocks.However,the results show that,Vpis highly dependent on the propagation direction,which means that the samples are seismically anisotropic(Figs.3 and 4).

The results from bothVpandVsmeasurements are summarized in Table 2 and Figs.3-6.In samples A,B and C2,Vpis the fastest when propagating inxdirection,parallel to the rocks lineation.Additionally,in both samples A(eclogite)and B(retrograde eclogite),the slowestVpwas obtained perpendicular to the foliation of the rock(z-direction),i.e.Vp-x＞Vp-y＞Vp-zis true for samples A and B.

The behaviors of samples C1 and C2 are slightly different.Sample C1(like A and B)has its slowest P-wave propagation in the direction perpendicular to the foliation,however,within thexyplane,the waves travel faster iny-direction than that inx-direction.In sample C2,the behavior varies with pressure.Up to a pressure of 200 MPa, the same is true as in samples A and B,i.e.Vp-x＞Vp-y＞Vp-z.At higher pressures,however,the waves in thez-direction are faster than that in they-direction,with this difference being in the order of 1%only.

The seismic anisotropy itself is calculated as

Seismic anisotropy is highest during the nonlinear part of the experiment and becomes relatively constant during the linear part.Anisotropy is highest for the eclogite(sample A,10%)and lowest for the retrograde eclogite(sample B,2%)(Fig.3).The granulites have similar anisotropies in the orders of 3%(C1)and 4%(C2)(Fig.4).

In order to derive pressure independent information on howVpandVsof the studied rocks are affected by temperature changes measurements during decreasing temperature were carried out at a constant pressure of 600 MPa,which is needed to ensure the best signal transmission through the sample.The results from all four samples show thatVpandVsdecrease with increasing temperature.Additionally,the P-wave anisotropy changes in response to temperature changes.With increasing temperature,the anisotropy increases for samples A,B and C2,while it decreases for sample C1.

As mentioned above,the S-wave velocities follow the same general trend as the P-wave velocities,i.e.they increase with pressure and decrease with increasing temperature.This is also true for the different polarization directions of the shear waves.

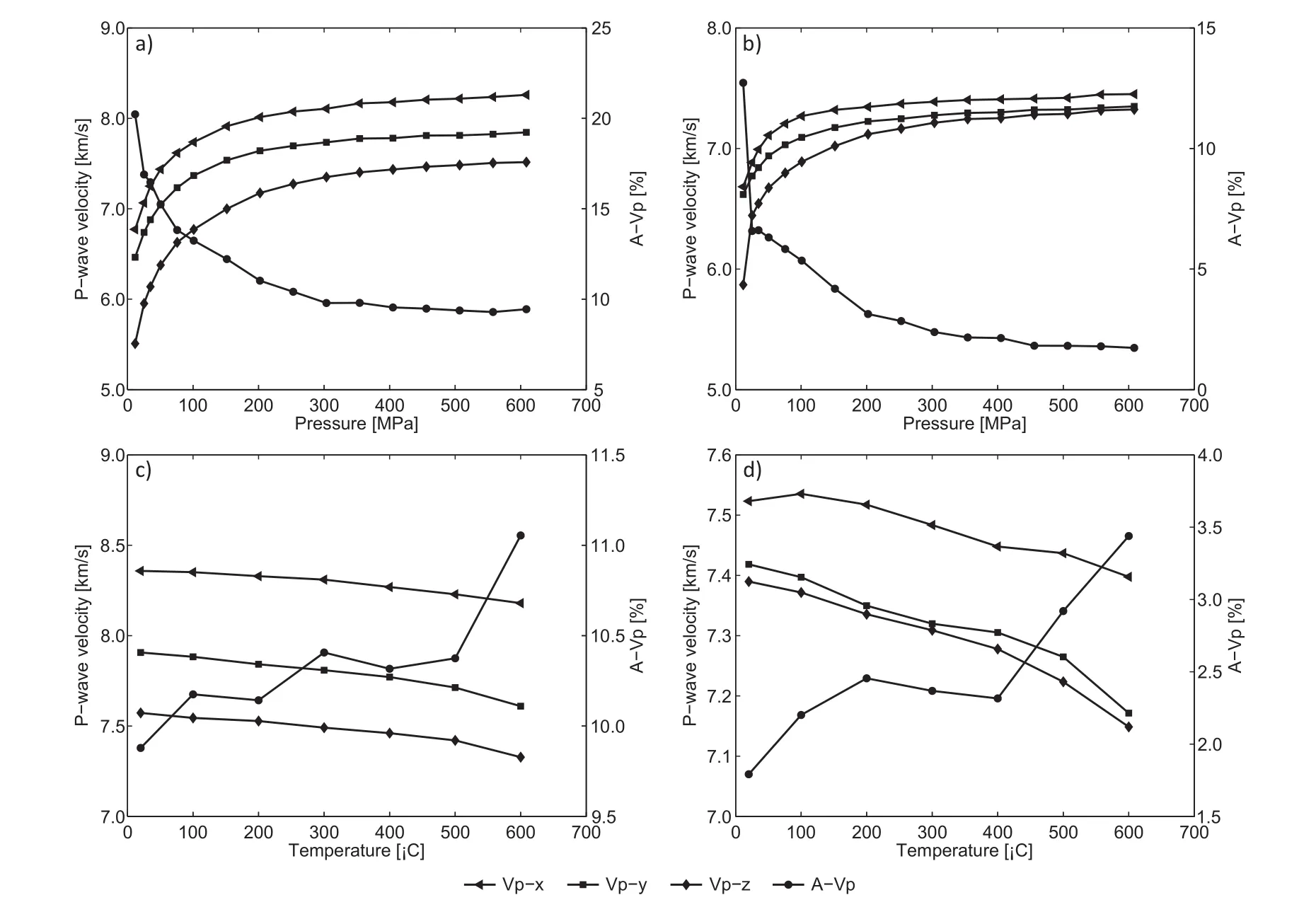
Fig.3.P-wave velocities in x,y,and z direction and the resulting P-wave anisotropy of the investigated eclogites in dependence of pressure(a and b)and temperature(c and d).Sample A is depicted in(a)and(c)and sample B in(b)and(d).

Fig.4.P-wave velocities and corresponding P-wave anisotropy of granulite samples C1(a and c)and C2(b and d)with respect to pressure(a and b)and temperature(c and d).

Table 2Summary of the mean elastic wave velocities,density,and elastic moduli as a function of pressure and temperature.

Fig.5.S-wave velocities of samples A(a and c)and B(b and d)with respect to changes in pressure(a and b)and temperature(c and d).The black lines represent mean velocities for each propagation direction(x,y,and z)and the blue lines show the difference between polarization directions(in%)for each propagation direction.

The difference between the two shear-wave components(polarization directions)is generally related to the relationship between the P-wave velocity and the fabric of the rock.In all samples,for exampleVp-x＞Vp-zand in agreement with that the two polarizations of the S-wave iny-direction(Vs-xyandVs-zy)have the same relationship,i.e.Vs-xy＞Vs-zy(Figs.5 and 6).This relationship is true for all polarization directions in sample A.In samples B and C2,the correlation holds in two directions(xandy)with the exception of S-waves propagating perpendicular to the foliation(zdirection).However,in sample C1,this link can only be implied fromwaves traveling in they-direction and it is inverse for waves inx-andz-direction.

Fig.6.Granulite S-wave velocities in dependence of pressure(a and b)and temperature(c and d)of samples C1(a and c)and C2(b and d)shown as mean velocities for each propagation direction in black.The blue lines show the corresponding difference for polarization directions(in%)for each propagation direction(x,y,and z).

It has to be noted that while the differences in S-wave velocity are relatively constant in the range of higher pressures(above 250-300 MPa),they vary unsystematically in the lower pressure range.

5.2.Density,volumetric strain and elastic moduli

The densities of the samples were calculated as a function of pressure and temperature from the measuredVpandVsand the dry density measured before each experiment.The densities of all samples increased almost linearly with pressure(Fig.7).On the other hand,with increasing temperature,the density of the samples decreased.A consistent relationship between velocity and density is evident,i.e.the higher the density,the higher the P-and S-wave velocities(Table 2,Figs.3,4 and 7).Furthermore,the velocity increase with the decrease in temperature as well as the increase in pressure is considered to be a typical behavior of natural rocks.

The effect of pressure and temperature on volumetric strain are shown in Fig.8.Pressure and temperature induced deformations were measured in all six directions with the help of 12 strain measurement gages.We report compression as a positive value and expansion as a negative value.The resulting stress-strain and thermal stress-strain curves increase as a function of pressure and decrease as a function of temperature(Fig.8).Since the applied pressure and temperature conditions are isotropic,the samples did not sustain any failure during the experiments.The relationships between volumetric strain vs.pressure(Fig.8 left)and volumetric strain vs.temperature(Fig.8 right)are proportional to the changes in density with pressure and temperature.

Fig.7.Density as a function of(a)pressure and(b)temperature for samples A,B,C1 and C2.

Fig.8.Volumetric strain as a function of(a)pressure and(b)temperature for samples A,B,C1 and C2.

Similar to the P-and S-wave velocities,the Poisson’s ratio increases with pressure in a nonlinear fashion up to approximately 200-250 MPa after which the increase becomes moderate and linear(Fig.9).The Poisson’s ratio of the eclogite samples(A and B)is significantly lower than that of the granulite(C1 and C2).For all rock types,the Poisson’s ratio is more or less unaffected by temperature changes,and the minor variations(Fig.9)are random and can be considered as within the measurement uncertainty(Motra et al.,2013,2014a,b,2016).

The average values for the Young’s(E),bulk(K)and shear(μ)moduli of sample A are presented in Fig.10 as a function of pressure and temperature.Deviations are again closely related to changes in P-and S-wave velocity of the corresponding sample,i.e.they increase with pressure and decrease with increasing temperature.

6.Discussion

VpandVsmeasured during increasing pressure along three perpendicular directions of the sample cubes showed a rapid increase in velocity up to pressures of approximately 200-250 MPa,followed by a subtle and almost linear increase with pressure.This characteristic is typical for such experiments(e.g.Kern et al.,1997).The initial rapid increase in P-and S-wave velocities results from the closure of microcracks that any metamorphic rock has after exhumation.The following linear increase reflects the specific properties of the analyzed rock and is mainly influenced by its modal abundance of the mineral rock forming minerals.Our results show that although the investigated samples have only minor variations in chemical composition,their mean P-and S-wave velocities vary significantly due to their variability in mineral assemblage,i.e.the P-and S-wave velocities of eclogites are higher than those of granulites.The alteration of eclogite reintroduces seismically slower mineral phases(mostly feldspar)and hence lowers the bulk velocity of the aggregate.

Fig.9.Poisson’s ratio as a function of(a)pressure and(b)temperature for samples A,B,C1 and C2.

Fig.10.Dynamic moduli(Young’s modulus(E),bulk modulus(K),and shear modulus(μ))as a function of(a)pressure and(b)temperature for eclogite sample A.

The differences inVpbetween the three different propagation directions within one sample are essentially a result of the rocks fabric.More precisely,the orientation of the minerals(SPO)contained within the sample primarily forms the rocks fabric and subsequently produces the anisotropy observed in P-wave velocities(see also Kern et al.,1997).For this reason,the highest P-wave anisotropy is produced in the unaltered eclogite sample(sample A,～10%),which is well foliated and has the strongest SPO.The retrograde eclogite(sample B),however,has a low anisotropy of～2%,although the rock is macroscopically well foliated.This can be attributed to the fine-grained and randomly oriented symplectites that essentially neutralize the P-wave anisotropy.The granulites(samples C1 and C2)on the other hand have a coarse foliation and no dominant SPO,resulting in low anisotropies of 3-4%.

To understand the P-wave anisotropy of the investigated samples it is essential to understand how the propagation directions(x,yandz)relate to each other in terms of theirVp.In this regard,the relationshipVp-x＞Vp-y＞Vp-zwould be expected.This holds true for samples A and B,i.e.the well foliated rocks.This,however,is not the case for samples C1 and C2 which represent the less or unfoliated granulites(C1:Vp-y＞Vp-x＞Vp-z,C2:Vp-x＞Vp-z＞Vp-y).This indicates that the more foliated a natural rock is,the larger the probability of the expected relationship to be accurate.

The variations ofVpwith temperature observed in this study reflect the intrinsic rock properties of the investigated samples.Higher temperatures induce expansion of the mineral phases and hence lower their density. This results in the observed decrease ofVp.

The difference in S-wave velocity between two orthogonally polarized shear wave components measured along a mutual propagation direction(shear wave splitting)is more complicated to be predicted.It seems that in most cases,it can be related to the information extracted fromVp,e.g.in all samples investigated in this study,Vp-xis larger thanVp-zand subsequentlyVs-xy＞Vs-zy.However,this is not always the case.Principally,the velocity for a specific S-wave results from the interplay between its propagation direction and its polarization direction,meaning that both have an influence on the resulting S-wave velocity.This also implies that likeVp,Vsmainly depends on the mineral assemblage and the SPO of the investigated rocks.

It has been suggested that the greater the difference inVsbetween the two orthogonal shear wave components,the higher the anisotropy(Kern et al.,1997,2001;Scheu et al.,2006;Motra and Wuttke,2016).Accordingly,the sample with the highest P-wave anisotropy(sample A)also has the highest average difference between the shear wave components.The change inVsaccompanied with the change in polarization directions is typically the type ofVsvariation used for studying reservoir azimuthal anisotropy.

The density of the investigated samples increases linearly with pressure and decreases linearly with increasing temperature.This reflects that higher pressures lead to compaction of the sample and subsequently a higher density and higher temperatures lead to expansion and subsequently lower densities.However,the rapid increase observed inVpandVsat lower pressures is not apparent in the changes in density for the same pressure range.This implies that the effects of microcracks on density are significantly smaller than they are on seismic velocities.Hence,P-and S-wave velocities are more sensitive to fracturing of the rock.

Additionally,the volumetric strain of the samples during the experiments increases rapidly up to about 100MPa before it passes into an almost linear increase,and is therefore less sensitive to the pressure increase than the seismic velocities which increase rapidly up to 200-250MPa. The same is true for the elastic moduli(Poisson’s ratio,Young’s modulus,bulk modulus and shear modulus).This is mostly due to the fact that they are calculated from both P-and S-wave velocites and therefore unexpected changes in one can be reduced in magnitude by the behavior of the other.In sample C2,for example,the Poisson’s ratio decreases between 34 MPa and 200 MPa,which is contrary to the behavior of the other samples.The reason for this is that in this pressure range, the increase in meanVpis lower than in the other samples and the increase inVsis significantly higher than that in the other samples.Most likely,the effect of a preferred microcrack orientation in sample C2 results in a negative trend in Poisson’s ratio.

In terms of engineering applications,the results for P-wave anisotropy in the pressure range from 12 MPa to 200 MPa are extremely important.As previously mentioned,the anisotropy here is significantly higher and produced by microcracks.Such information can be used to predict the orientation of fractures in the underlying rock before or during construction.Additionally,this implies that such fractures will only be closed at depths of around 6-7 km when assuming a typical pressure gradient.

7.Conclusions

In this study,the basic elastic and geomechanical properties of four rock samples were measured and analyzed using laboratory measurements.We determined compressional wave velocities(Vp)and orthogonally polarized shear wave velocities(Vs1,Vs2)as a function of pressure as well as temperature using a true triaxial multianvil apparatus.

The effects of the applied pressure and temperature on rocks and their physical properties are considered to be reversible changes that occur at changing pressure and temperature conditions.In metamorphic rocks,increasing pressure leads to increasing velocities,and increasing temperature leads to decreasing velocities.

The general increases ofVpandVswith increasing pressure are the result of the sample compaction,as is confirmed by the volumetric strain vs.pressure(Fig.8 and Table 2)and density vs.pressure relationships(Fig.7 and Table 2).TheVpandVsdecreasing with temperature result from the expansion of the samples,i.e.lower densities.TheVpandVschanges are most likely affected by the changes in the contact conditions at grain boundaries and microcracks.

An increase in velocity under the influence of applied pressure in the lower pressure range was primarily due to the closure of preexisting microcracks.This closure improves the contact between rock-forming minerals.At higher pressures(above 250 MPa),this first compaction of the aggregate is nearly complete.As the seismic wave propagation is related to the geomechanical properties of rocks,in particular to the elastic moduli,the change in seismic wave velocities involves a change in geomechanical properties of rocks.

The velocity anisotropy is linked to the fabric of the samples.Rocks with a high anisotropy show a pronounced shape preferred orientation.In general,the elastic,bulk,and shear moduli of the metamorphic rocks decrease with increasing temperature.The relationship between the Young’s,bulk,and shear moduli as well as density,Poisson’s ratio,and volumetric strain with elasticVpandVsare valuable for understanding metamorphic rocks.

Conflicts of interest

The authors wish to confirm that there are no known conflicts of interest associated with this publication and there has been no significant financial support for this work that could have influenced its outcome.

Alm O,Jakeland LL,Kou SQ.The influence of microcrack density on the elastic and fracture mechanical properties of Stripa granite.Physics of the Earth and Planetary Interiors 1985;40(3):161-79.

Ashby MF,Sammis CG.The damage mechanics of brittle solids in compression.Pure and Applied Geophysics 1990;133(3):489-521.

Balme MR,Rocchi V,Jones C,Sammonds PR,Meredith PG,Boon S.Fracture toughness measurements on igneous rocks using a high pressure,high temperature rock fracture mechanics cell.Journal of Volcanology and Geothermal Research 2004;132:159-72.

Bauer SJ,Friedman M,Handin J.Effects of water-saturated on strength and ductility of three igneous rocks at effective pressures to 50 MPa and temperatures to partial melting.In:Einstein HH,Scandriato DP,editors.Rock mechanics from research to application.Rotterdam:A.A.Balkema;1981.p.79-84.

Batzle ML,Simmons G,Siegfried RW.Microcrack closure in rocks under stress:direct observation.Journal of Geophysical Research:Solid Earth 1980;85:7072-90.

Benson PM,Vinciguerra S,Meredith PG,Young RP.Laboratory simulation of volcano seismicity.Science 2008;322:249-52.

Carpenter DL.Tectonic history of the metamorphic basement rocks of the Sierra del Carmen,Coahuila,Mexico.Geological Society of America Bulltin 1997;109:1321-32.

Cordonnier B,Hess KU,Lavalle Y,Dingwell DB.Rheological properties of dome lavas:case study of Unzen volcano.Earth and Planetary Science Letters 2009;279:263-72.

Cheatham JB.The effect of pressure,temperature,and loading rate on the mechanical properties of rocks.In:Lindholm US,editor.Mechanical behaviour of materials under dynamic loads.New York:Springer-Verlag;1968.p.388-401.

D’Andrea DV,Fischer RL,Fogelson DE.Prediction of compressive strength from other rock properties.US Bureau of Mines;1966.Report of Investigations 6702.

Deere DU,Miller RP.Engineering classification and index properties for intact rock.Technical Report.Kirtland Base,N.M.:US Air Force Weapons Laboratory;1966.AFWL-TR-65-116.

Duclos R,Paquet J.High-temperature behaviour of basalt-role of temperature and strain rate on compressive strength and KIC toughness of partially glassy basalts at atmospheric pressure.International Journal of Rock Mechanics and Mining Science&Geomechanics Abstracts 1991;28:71-6.

Feng ZJ,Zhao YS,Zhou AC,Zhang N.Development program of hotdryrock geothermal resource in the Yangbajing Basin of China.Renew Energy 2012;39:490-5.

Fredrich JT,Wong TF.Micromechanics of thermally induced crack in the crustal rocks.Journal of Geophysical Research 1986;91:12743-64.

Gebrande H,Kern H,Rummel F.Elasticity and inelasticity. In:Hellwege K-H,editor.Landolt-Brnstein.Numerical data and functional relationships in science and technology.Berlin:Springer-Verlag;1982.p.1-233.New Series;Group V.Geophysics and Space Research.Vol.1b:Physical Properties of Rocks.

Gibb FGF.High-temperature,very deep,geological disposal:a safer alternative for high-level radioactive waste.Waste Management 1999;19:207-11.

Griggs DT,Turner FJ,Heard HC.Chapter 4:deformation of rocks at 500 to 800°C.Geological Society of America 1960;79:39-104.

Handin J,Carter N.Rheological properties of rock at high temperatures.Proceedings of the Congress of the International Society for Rock Mechanics 1979;4:97-106.

Heap MJ,Vinciguerra S,Meredith PG.The evolution of elastic moduli with increasing crack damage during cyclic stressing of abasalt from Mt.Etna volcano.Tectonophysics 2009;471:153-60.

Heap MJ,Faulkner DR,Meredith PG,Vinciguerra S.Elastic moduli evolution and accompanying stress changes with increasingc rack damage:implications for stress changes around fault zones and volcanoes during deformation.Geophysical Journal International 2010;183:225-36.

Heap MJ,Lavallée Y,Petrakova L,Baud P,Reuschlé T,Varley NR.Microstructural controls on the physical and mechanical properties of edifice-forming andesites at Volcáde Colima,Mexico.Journal of Geophysical Research:Solid Earth 2014;119:2925-63.

Heuze FE.High-temperature mechanical,physical and thermal properties of granitic rocks:a review.International Journal of Rock Mechanics and Mining Science&Geomechanics Abstracts 1983;20:310.

Hommand-Etienne F,Houpert R.Thermally induced micro-cracking in granites:characterisation and analysis.International Journal of Rock Mechanics and Mining Science&Geomechanics Abstracts 1989;26:125-34.

Inada Y,Yorkota K.Some studies of low temperature rock strength.International Journal of Rock Mechanics and Mining Science&Geomechanics Abstracts 1984;21:145-53.

International Society for Rock Mechanics(ISRM).The complete ISRM suggested methods for rock characterization,testing and monitoring:1974-2006.In:Ulusay R,Hudson JA,editors.Suggested methods prepared by the commission on testing methods;2007.

Kendrick JE,Smith R,Sammonds P,Meredith PG,Dainty M,Pallister JD.The influence of thermal and cyclic stressing on the strength of rock from Mount St.Helens,Washington.Bulletin of Volcanology 2013a;75:1-12.

Kendrick E,Lavalle Y,Hess KU,Heap MJ,Gaunt HE,Meredith PG,Dingwell DB.Tracking the permeable porous network during strain-dependent magmaticflow.Journal of Volcanology and Geothermal Research 2013b;260:117-26.

Kern H.The effect of high temperature and high confining pressure on compressional wave velocities in quartz-bearing and quartz-free igneous and metamorphic rocks.Tectonophysics 1978;44:185-203.

Kern H,Liu B,Popp T.Relationship between anisotropy of P and S wave velocities and anisotropy of attenuation in serpentinite and amphibolite.Journal of Geophysical Research:Solid Earth 1997;102(B2):3051-65.

Kern H,Popp T,Gorbatsevich F,Zharikov A,Lobanov KV,Smirnov YP.Pressure and temperature dependenceVpandVsin rocks from the superdeep well and from the surface analogues at Kola and the nature of velocity anisotropy.Tectonophysics 2001;338:113-34.

Kueppers U,Scheu B,Spieler O,Dingwell DB.Fragmentation efficiency of explosive volcanic eruptions:a study of experimentally generated pyroclasts.Journal of Volcanology and Geothermal Research 2006;153:125-35.

Lama RD,Vutukuri VS.Handbook on mechanical properties of rocks,vol.II.Clausthal:Trans Tech Publications;1978.

Lavalle Y,Hess KU,Cordonnier B,Dingwell DB.Non-Newtonian rheological law for highly crystalline dome lavas.Geology 2007;35:843-6.

Lavalle Y,Meredith PG,Dingwell DB,Hess KU,Wassermann J,Cordonnier B,Gerik A,Kruhl JH.Seismogenic lavas and explosive eruption forecasting.Nature 2008;453:507-10.

Loaiza S,Fortin J,Schubnel A,Gueguen Y,Vinciguerra S,Moreira M.Mechanical behavior and localized failure modes in a porous basalt from the Azores.Geophysical Research Letters2012;39(19).https://doi.org/10.1029/2012GL05321.

Merriam R,Rieke HH,Kim YC.Tensile strength related to mineralogy and texture of some granitic rocks.Engineering Geology 1970;4:155-60.

Moradian ZA,Behnia M.Predicting the uniaxial compressive strength and static Young’s modulus of intact sedimentary rocks using the ultrasonic test.International Journal of Geomechanics 2009;9:1-14.

Motra HB,Osburg AD,Hildebrand J.Uncertainty quantification on creep deflection of concrete beam subjected to cyclic loading.In:Safety,Reliability,Risk and Life-Cycle Performance of Structures and Infrastructures-Proceedings of the 11th International Conference on Structural Safety and Reliability;2013.

Motra HB,Dimmig-Osburg A,Hildebrand J.Quality assessment of models with an application to cyclic creep prediction of concrete.International Journal of Reliability and Safety 2014a;8(2-4):262-83.

Motra HB,Hildebrand J,Dimmig-Osburg A.Influence of specimen dimensions and orientation on the tensile properties of structural steel.Materialpruefung/Materials Testing 2014b;56(11-12):929-36.

Motra HB,Stutz H,Wuttke F.Quality assessment of soil bearing capacity factor models of shallow foundations.Soils and Foundations 2016;56(2):265-76.

Motra HB,Wuttke F.Temperature dependence of elastic P-and S-wave properties of rocks:applications to geothermal reservoir evaluation.In:Energy geotechnics proceedings of the 1st international conference on energy geotechnics(ICEGT 2016,Kiel,Germany,29-31 August;2016.p.311-6.

Nakaten N,Schluter R,Azzam R,Kempka T.Development of a techno-economic model for dynamic calculation of cost of electricity,energy demand and CO2emissions of an integrated UCG-CCS process.Energy 2014;66:779-90.

Nye JF.Physical properties of crystals-their representation by tensors and matrices.UK:Oxford University Press;1985.

Prikryl R.Some micro-structural aspects of strength variation in rocks.International Journal of Rock Mechanics and Mining Sciences 2001;38:671-82.

Punturo R,Kern H,Cirrincione R,Mazzoleni P,Pezzino A.P-and S-wave velocities and densities in silicate and calcite rocks from the Peloritani Mountains Sicily(Italy):the effect of pressure,temperature and the direction of wave propagation.Tectonophysics 2005;409:55-72.

Ringwood AE.Disposal of high-level nuclear wastes-a geological perspective.Mineralogical Magazine 1985;49:159-76.

Rocchi V,Sammonds PR,Kilburn CR.Flow and fracture maps for basaltic rock deformation at high temperatures.Journal of Volcanology and Geothermal Research 2003;120(1-2):25-42.

Rocchi V,Sammonds PR,Kilburn CRJ.Fracturing of Etnean and Vesuvian rocks at high temperatures and low pressures.Journal of Volcanology and Geothermal Research 2004;132(2-3):137-57.

Rummel F,Van Heerden WL.Suggested methods for determining sound velocity.International Journal of Rock Mechanics and Mining Science&Geomechanics Abstracts 1978;15(2):53-8.

Sammis CG,Ashby MF.The failure of brittle porous solids under compressive stress states.Acta Metallurgica 1986;34:511-26.

Sanchez M,Gens A,Guimaraes L.Thermal-hydraulic-mechanical(THM)behaviour of a large-scale in situ heating experiment during cooling and dismantling.Canadian Geotechnical Journal 2012;49(10):1169-95.

Sarkar K,Vishal V,Sign TN.An empirical correlation of index geomechanical parameters with the compressional wave velocity.Geotechnical&Geological Engineering 2012;30:469-79.

Scheu B,Kern K,Spieler O,Dingwell DB.Temperature dependence of elastic P-and S-wave velocities in porous Mt.Unzen dacite.Journal of Volcanology and Geothermal Research 2006;153:136-47.

Scheu B,Kueppers U,Mueller S,Spieler O,Dingwell DB.Experimental volcanology on eruptive products of Unzen volcano.Journal of Volcanology and Geothermal Research 2008;175:110-9.

Scholz CH.Microfracturing and the inelastic deformation of rock in compression.Journal of Geophysical Research 1968;73:1417-32.

Schön JH.Physical properties of rocks:a workbook.Elsevier;2011.

Simmons G,Cooper HW.Thermal cycling cracks in three igneous rocks.International Journal of Rock Mechanics and Mining Sciences 1978;15:145-8.

Smith R,Sammonds PR,Kilburn CR.Experimental studies of lava dome fracture.In:AGU fall meeting abstracts;2005.

Smorodinov MI,Motovilove EA,Volkov VA.Determination of correlation relationships between strength and some physical characteristics of rocks.Proceedings of the Congress of the International Society for Rock Mechanics 1970;1:1-19.

Spieler O,Kennedy B,Kueppers U,Dingwell DB,Scheu B,Taddeucci J.The fragmentation threshold of pyroclastic rocks.Earth and Planetary Science Letters 2004;226:139-48.

Tapponnier P,Brace WF.Development of stress-induced micro-cracks in Westerly granite.International Journal of Rock Mechanics and Mining 1976;13:103-12.

Vinciguerra S,Trovato C,Meredith PG,Benson PM.Relating seismic velocities,thermal cracking and permeability in Mt.Etna and Iceland basalts.International Journal of Rock Mechanics and Mining Sciences 2005;42:900-10.

Wai RSC,Lo KY,Rowe RK.Thermal stress analysis in rocks with non-linear properties.International Journal of Rock Mechanics and Mining Science&Geomechanics Abstracts 1982;19:211-20.

Watts AB,Platt JP,Buhl P.Tectonic evolution of the Alboran Sea basin.Basin Research 1993;5:153-77.

Wuttke F,Sattari AS,Rizvi ZH,Motra HB.Advanced meso-scale modelling to study the effective thermo-mechanical parameter in solid geomaterial.In:Advances in Laboratory Testing and Modelling of Soils and Shales(ATMSS),part of the series Springer series in Geomechanics and Geoengineering;2017.p.85-95.

Youash Y.Dynamic physical properties of rocks:Part 2,Experimental result.In:Proceedings of the 2nd congress of the international society for rock mechanics,Beograd,Yugoslavia,21-26 September 1970.Beograd,Yugoslavia:Institute for Development of Water Resources;1970.p.185-95.