基于转移熵的银行间风险传染效应实证研究
李 智, 牛 晓 健
(1.复旦大学 应用经济学博士后流动站,上海 200433;2.复旦大学 经济学院,上海 200433)
一、引 言
在现代经济中金融机构间显著的特征是其具有高度的关联性,该关联性在带来诸多经济效应的同时也为金融机构间风险传染提供了渠道,一家或几家金融机构的风险可能会形成多米诺骨牌效应,造成金融系统性风险。随着金融市场的不断发展与完善,处于金融系统中的银行会通过各种直接或间接形式形成紧密的关联,而此关联正是银行间风险传染的基础。对银行间风险传染问题进行研究,将有利于维护银行系统的稳定,进而对整个金融系统的稳定运行也具有重要的实践意义。
自最近的全球性金融危机发生以来,金融风险传染问题引起了学术界和金融监管部门的广泛关注,如何度量银行间风险传染效应便是关注的热点问题之一。在目前已有研究中,对银行间风险传染效应研究的主流方法是网络分析法[1-5],该方法主要思想是假定部分银行因外部冲击而倒闭,进而基于银行间同业拆借关系,研究初始倒闭银行在银行系统中的传染过程。如Upper 和Worm基于德国银行同业拆借数据,研究结果显示:在没有安全网的前提下,银行失败可引发银行系统内大范围的风险传染;在任何情况下,只要同业拆借违约损失率超过40%,就会导致大范围的风险传染发生[1]。马君潞等基于我国银行资产负债表数据,采用网络分析法估算了我国银行系统的双边传染风险,分析了不同损失水平下单个银行倒闭及多个银行同时倒闭所引起的传染性[2]。廉永辉采用网络分析法估计了2007~2013年我国银行同业网络,在区分债权银行和债务银行的前提下,以网络联系强度为权重计算了各银行同业业务对手的总风险,进而研究了同业业务对手总风险对自身风险的影响[4]。Cao等基于中国2008~2015年21家银行数据,构建银行同业网络,进而采用超链接分析的主题搜索算法分析该网络,并分析银行间风险传染水平[5]。
此外,由于资本市场交易数据相对容易获得,学者们开始借助资本市场数据研究银行间风险传染效应[6-15],而较多的是运用风险价值、条件风险价值或边际预期损失等技术研究银行系统性风险溢出效应,或者结合资产负债表对银行系统的风险传染以及系统重要性银行进行鉴别。如赵进文和韦文彬基于我国14家上市银行2007年10月7日至2012年5月31日的数据,运用边际期望损失方法度量了我国银行业系统性风险贡献度[7];方意等结合或有权益分析法和有向无环图技术,从时间和横截面维度研究了我国银行系统性风险,并对系统重要性银行进行了鉴别[9];Reboredo和Ugolini采用2003年1月到2015年3月西班牙银行业数据,基于条件风险价值方法研究了西班牙上市银行的系统性风险[10]。Anghelache和Oanea基于条件风险价值方法,研究了罗马尼亚商业银行间风险传染及其影响因素[14]。Mensah和 Premaratne基于条件风险价值方法,实证研究了亚洲银行机构系统性贡献[15]。
鉴于银行股票价格波动能够反映其风险信息,因此可以利用银行股票价格波动作为反映银行风险的度量指标,而银行间风险传染效应便是银行风险信息在银行间传递的结果。所以可以从银行风险信息在银行间传递角度,展开对银行间风险传染效应的度量。转移熵为度量银行风险信息传递提供了一种有效的工具,其不仅能够分析银行间风险信息相互作用,而且能够衡量风险信息传递的方向性。因此,本文以我国16家上市银行为研究对象,采用转移熵方法度量银行间风险传染效应,以期为银行风险管理和维护金融系统稳定提供决策依据。
二、研究方法
1.转移熵
熵的概念是由Rudolf Clausius于1850年提出的物理概念,用于衡量系统中能量的分布是否均匀。而将熵的概念引入到信息传递中是Shannon,他于1948年提出了信息熵的概念。Schreiber于2000年给出了转移熵的定义,其能够分析系统之间信息的相互作用,且包含了系统之间信息传递的方向,因此,转移熵含有定向与动态的信息。其中转移熵的具体定义如下[16]:
(1)
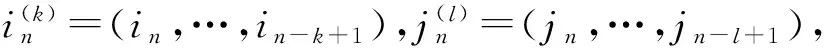
2.银行间风险传染度量
银行所有与盈利或风险相关的信息反映在其股票价格中,股票价格波动是银行风险行为的总体体现[20]。因此,本文利用银行股票价格波动作为反映银行风险的指标。假设有N家银行,PI(t)表示银行I的股票在第t日的收盘价,则银行I的股票在第t日的对数收益率为:
YI(t)=lnPI(t)-lnPI(t-1)
(2)
进而可以得到银行风险指标σI(t),即对数收益率的标准差:
(3)
基于上述定义得到任意两个银行的风险指标序列,均可以定义两者间的转移熵。对于银行I和银行J的风险时间序列,根据Schreiber提出的转移熵概念,可定义转移熵TEJ→I(k,l),其度量的是银行J的风险信息对银行I风险的影响,此值越大意味着银行J对银行I的风险传染效应越大。TEJ→I(k,l)具体表达式如下:
(4)
其中,in和jn分别表示的是银行I和银行J的风险时间序列的第n个元素。通常为了计算方便,一般假设k=l=1,因此,上述公式(4)简化为:
(5)
根据转移熵上述定义可知:TEJ→I(k,l)不是对称的,所以TEJ→I(k,l)≠TEI→J(k,l)。因此,转移熵可以有效度量银行间风险传染效应大小及其方向性。
三、实证研究
本文选取中国16家上市银行从2012年1月至2016年11月的收盘价作为数据来源,16家上市银行分别为浦发银行、华夏银行、民生银行、招商银行、南京银行、兴业银行、北京银行、农业银行、交通银行、工商银行、光大银行、建设银行、中国银行、中信银行、平安银行、宁波银行。为了描述简便,对此16家银行分别用B1~B16进行表示。在度量银行风险时,我们将银行股票期间进行时间窗口划分,其中采用时间间隔为20个交易日,单个时间窗口长度为28个交易日。
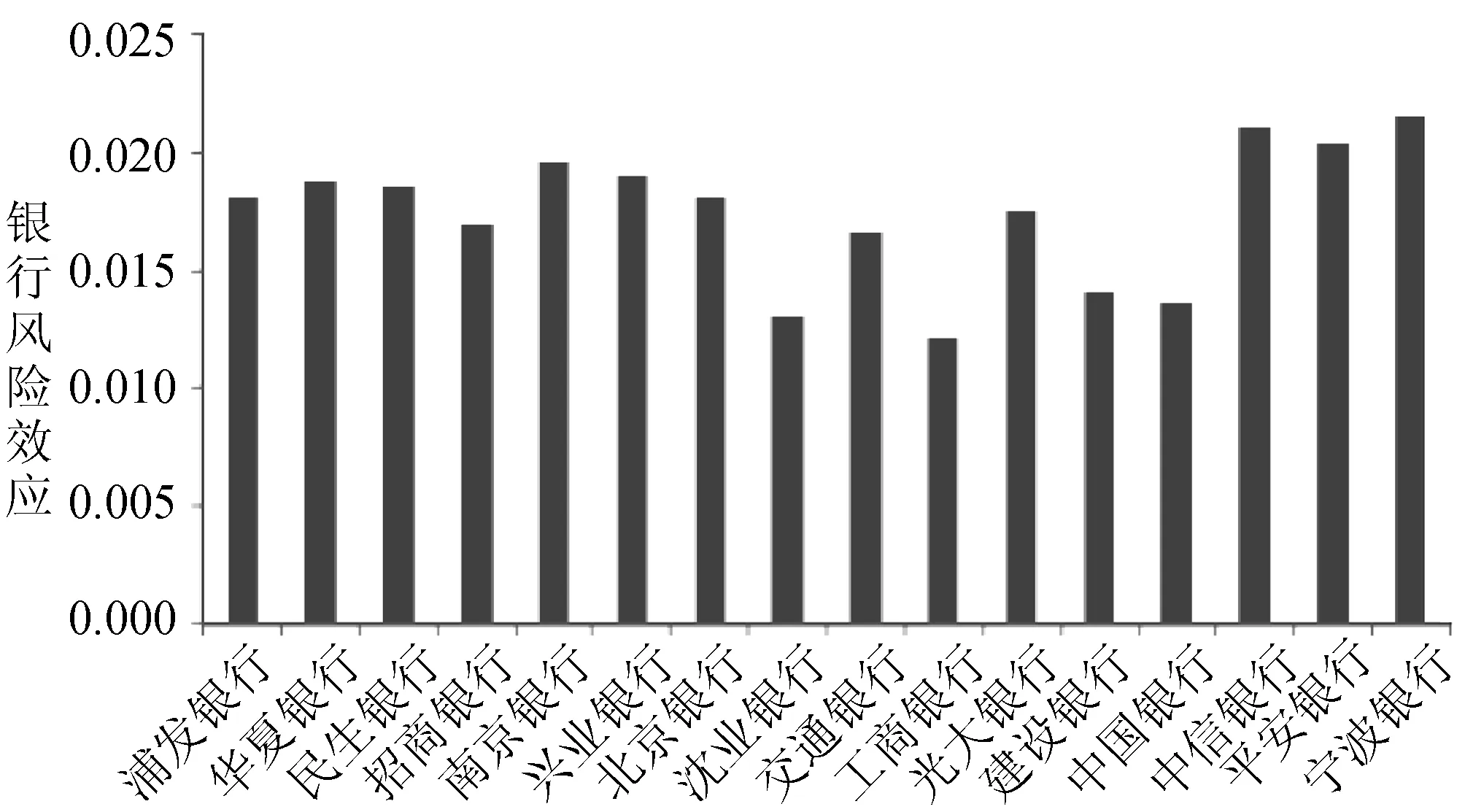
图1 上市银行的风险效应
1.银行风险效应
基于本文选取的样本及其数据,可以得到每个时间窗口的银行风险效应,进而利用平均值作为2012年1月至2016年11月期间每个银行风险度量结果,如图1所示。从图1可知,本文研究期间内风险较大的3个银行分别是宁波银行、中信银行和平安银行,它们的风险分别为1.2716,1.2464和1.2027;而风险最小的银行是工商银行,其风险大小为0.7211。进而我们将每个时间窗口的16家银行风险大小的平均值作为银行整体风险效应,可以得到上市银行风险演变特征,如图2所示,其中m表示的是滑动的时间窗口数。由图2可知,在2012年1月至2016年11月期间,16家上市银行的整体风险处于波动状态,特别是m从33到46期间时银行整体风险处于较大的波动状态。原因在于此段时间窗口对应的时间区间为2014年8月至2015年10月,而此期间我国股票市场整体波动较大,银行业股票也不例外。
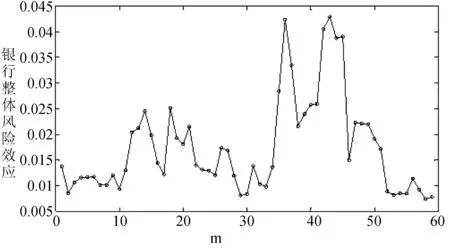
图2 上市银行的整体风险效应
2.银行间风险传染效应
在应用转移熵之前,需要对数据进行粗粒化处理,本文采用等概率分布方法,即以随机变量的分位数为阈值,将其等概率分为几类。在本文中选择0.2和0.8分位数进行三段分隔方法,当然也可以选择其他的分位数来粗粒化风险序列,但得到结果类似。基于转移熵计算公式,通过计算得到银行间风险传染效应结果,如表1所示。基于表1结果,可以分析单个银行对其他银行的风险传染效应。我们以浦发银行为例,其对其他15家银行的风险传染效应如图3所示。从图3可知,浦发银行对招商银行和交通银行风险传染效应最大,而对光大银行风险传染影响最小。
基于表1的银行间风险传染效应,我们可以进一步分析单个银行对其他15家银行的总的风险传染效应,以及其面临其他15家银行的总的风险传染效应,相应的结果分别如图4和图5所示。从图4可以发现,工商银行对其他银行总的风险传染效应最大,这意味在16家银行中工商银行是银行间风险传染的重要来源;而招商银行对其他银行总的风险传染效应最小,相比较而言,在16家银行中招商银行在风险传染中作用最小。由图5可知,交通银行面临的其他银行风险传染效应最大,这意味其面临的银行风险传染冲击最大,是最脆弱的银行;而光大银行面临风险传染效应最小,相对而言最稳健。
3.银行风险贡献度
在上述研究的基础上,我们进一步利用转移熵研究各个银行对银行业风险贡献度。为此,我们通过计算每家银行对银行行业指数的风险传染效应,作为其对银行业风险贡献度。本文选择的银行行业指数为801780.SL,通过转移熵计算可得到16家银行对银行行业风险的贡献度,如图6所示。可见,工商银行对银行业风险贡献度最大,为0.1806;交通银行对银行业风险贡献度次之,为0.1567;建设银行、中国银行和招商银行对银行业风险贡献度比较接近低于0.1500;在16家银行中,农业银行对银行业风险贡献度最小,为0.0851。
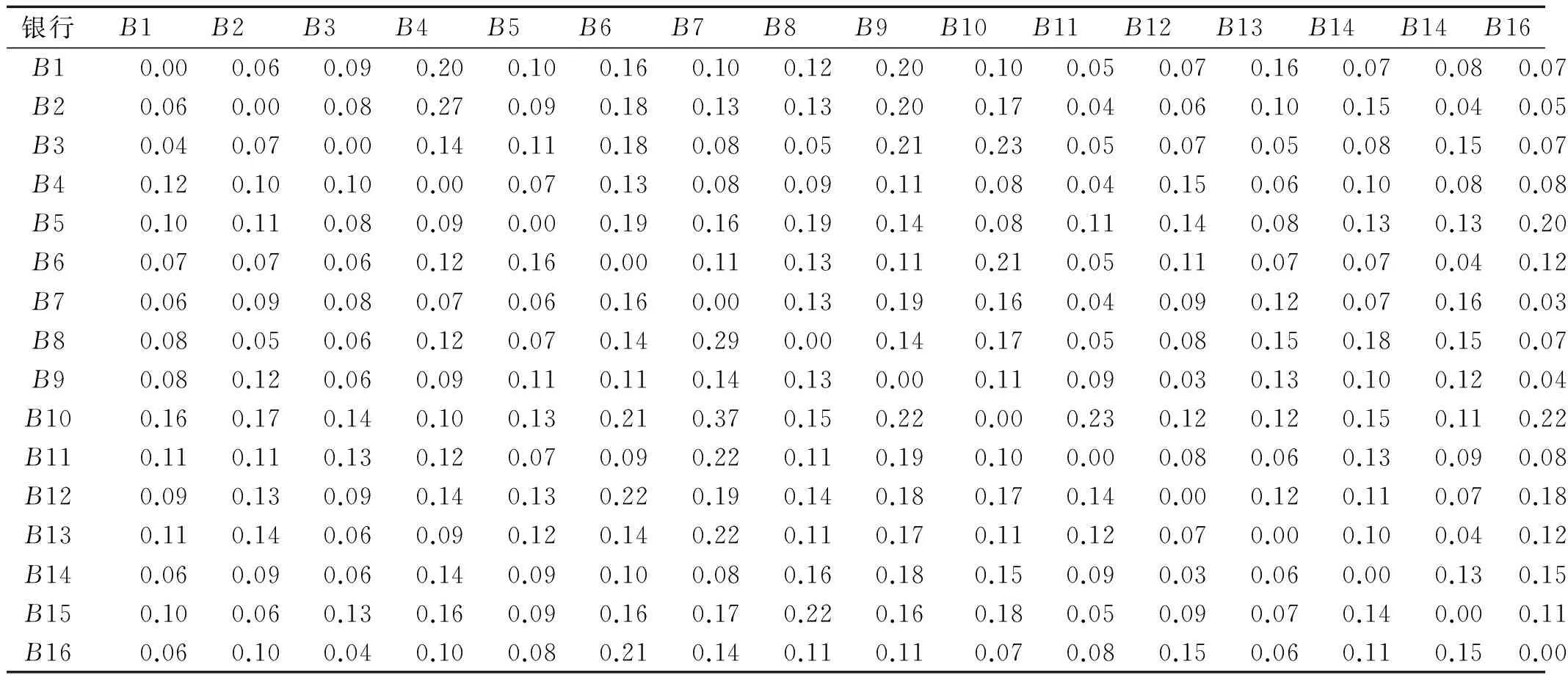
表1 银行间风险传染效应
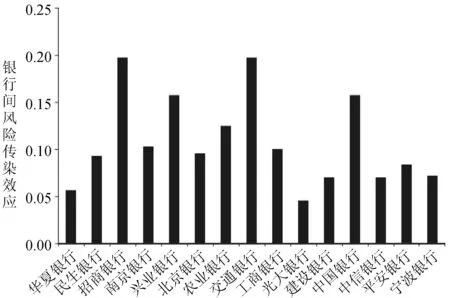
图3 浦发银行对其他银行的风险传染效应
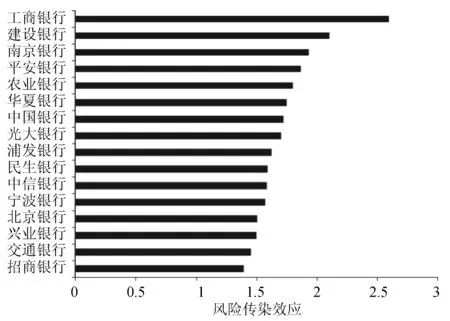
图4 银行对其他银行总的风险传染效应

图5 银行面临的其他银行风险传染效应
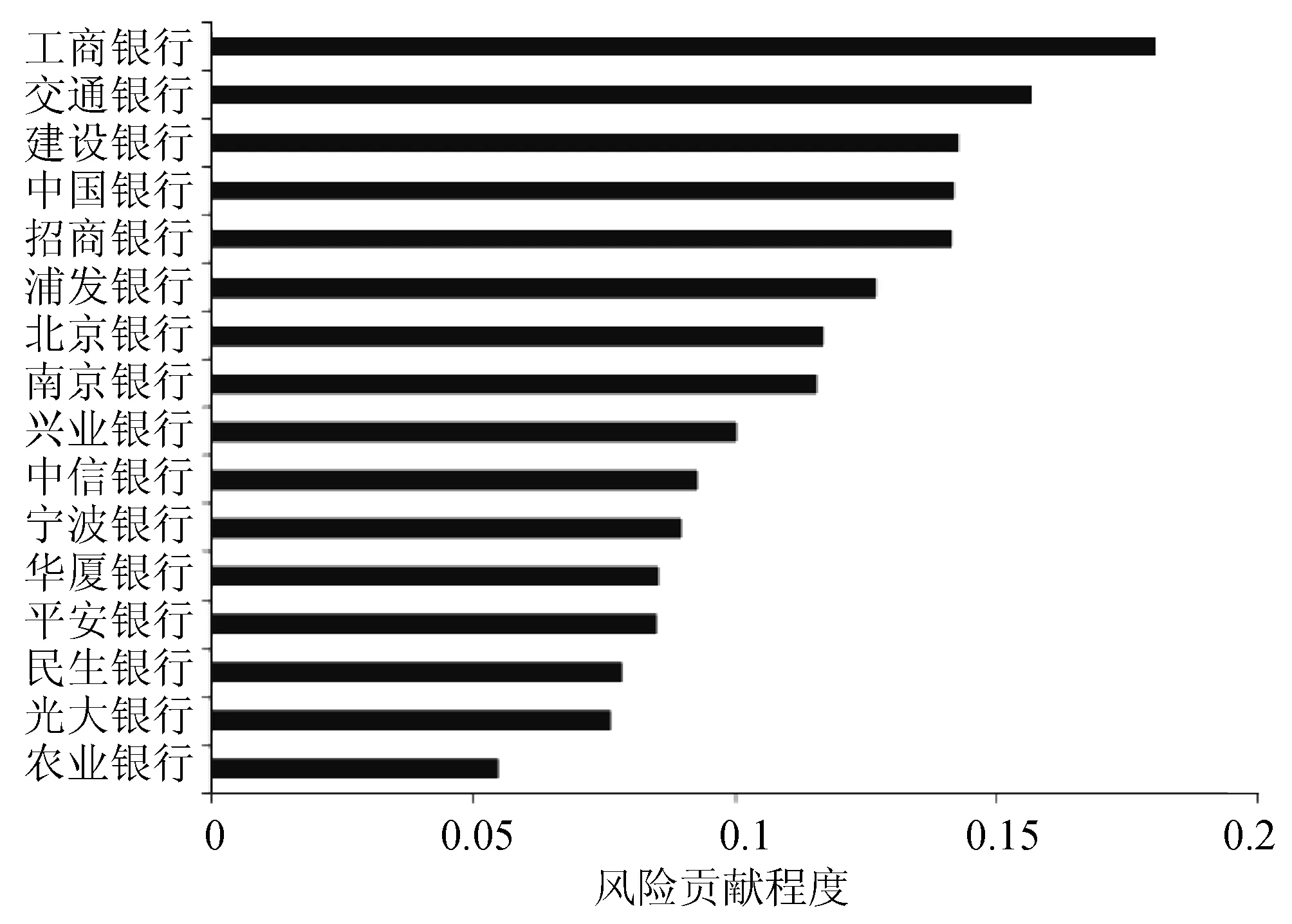
图6 银行对银行业风险贡献度
四、结 论
鉴于银行间风险传染度量对维护金融系统稳定具有重要的意义,同时资本市场交易数据相对容易获得,本文基于转移熵方法提出了一种新的度量银行间风险传染效应工具。基于2012年1月至2016年11月期间16家上市银行具体数据,对银行间风险传染效应进行了实证研究。实证研究表明:研究期间内风险较大的3个银行分别是宁波银行、中信银行和平安银行,而风险最小的银行是工商银行,16家上市银行的整体风险处于波动状态;工商银行对其他银行总的风险传染效应最大,而招商银行对其他银行总的风险传染效应最小;交通银行面临的其他银行风险传染效应最大,光大银行面临风险传染效应最小;工商银行对银行业风险贡献度最大,交通银行对银行业风险贡献度次之,农业银行对银行业风险贡献度最小。本文研究显示该方法不仅可以度量银行间风险传染效应,而且可以度量银行总的风险传染效应和银行对银行行业风险贡献度。这有利于识别出银行系统中系统重要性银行,为维护银行系统稳定提供决策依据。
[1] UPPER C,WORMS A. Estimating bilateral exposures in the German interbank market:is there a danger of contagion?[J]. European Economic Review,2004,48(4):827-849.
[2] 马君潞,范小云,曹元涛. 中国银行间市场双边传染的风险估测及其系统性特征分析[J]. 经济研究,2007(1):68-78.
[3] 周再清,谭盛中,王弦洲. 我国银行间市场传染性的风险测试[J]. 统计与决策,2008(16):45-46.
[4] 廉永辉. 同业网络中的风险传染——基于中国银行业的实证研究[J]. 财经研究,2016,42(9):63-74.
[5] CAO H,LI Y,CHEN W,et al. Systemic risk in China’s interbank lending market[J]. Journal of Mathematical Finance,2017(7):188-198.
[6] 杨有振,王书华. 中国上市商业银行系统性风险溢出效应分析——基于CoVaR 技术的分位数估计[J]. 山西财经大学学报,2013(7):24-33.
[7] 赵进文,韦文彬. 基于MES测度我国银行业系统性风险[J]. 金融监管研究,2012(8):28-40.
[8] LOPEZ-ESPINOSA G,MORENO A,RUBIA A,et al. Short-term wholesale funding and systemic risk:a global CoVaR approach[J]. Journal of Banking & Finance,2012,36(12):3150-3162.
[9] 方意,王道平,范小云. 我国银行系统性风险的动态特征及系统重要性银行甄别——基于CCA与DAG相结合的分析[J]. 金融研究,2013(11):82-95.
[10] REBOREDO J C,UGOLINI A. Systemic risk of Spanish listed banks:a vine copula CoVaR approach[J]. Spanish Journal of Finance and Accounting,2016,45(1):1-31.
[11] 吴恒煜,胡锡亮,吕江林. 我国银行业系统性风险研究——基于拓展的未定权益分析法[J]. 国际金融研究,2013(7):85-96.
[12] SALDIAS M. Systemic risk analysis using forward-looking distance-to-default series[J]. Journal of Financial Stability,2013,9(4):498-517.
[13] 刘孟飞,张晓岚. 中国上市银行系统性风险估计:模型与应用[J]. 大连理工大学学报(社会科学版),2013,34(1):54-60.
[14] ANGHELACHE G V,OANEA D C. Romanian commercial banks’ systemic risk and its determinants: a CoVAR approach[J]. International Journal of Academic Research in Accounting,Finance and Management Sciences,2016,6(3):96-109.
[15] MENSAH J O,PREMARATNE G. Systemic interconnectedness among Asian banks[J]. Japan and the World Economy,2017(41):17-33.
[16] SCHREIBER T. Measuring information transfer[J]. Physical Review Letters,2000,85(2):461-464.
[17] DIMPFL T,PETER F J. Using transfer entropy to measure information flows between financial markets[J]. Studies in Nonlinear Dynamics and Econometrics,2013,17(1):85-102.
[18] KWON O,YANG J S. Information flow between stock indices[J]. Europhysics Letters,2008,82(6):124-130.
[19] DIMA B,DIMAS M,BARNA F,et al. How to trade using the (Shannonian) transfer entropy? an application for Central and Eastern European markets[J]. Economic Computation and Economic Cybernetics Studies and Research,2014,48(2):57-73.
[20] SAUNDERS A,STROCK E,TRAVLOS N G. Ownership structure,deregulation,and bank risk taking[J]. Journal of Finance,1990,45(2):643-654.

