利用人工鱼群算法优化高斯过程模型及应用分析

邱小梦，周世健，王奉伟，欧阳亮酉

(1. 东华理工大学测绘工程学院，江西 南昌 330013； 2. 流域生态与地理环境监测国家测绘地理信息局重点实验室，江西 南昌 330013； 3. 南昌航空大学，江西 南昌 330063； 4. 同济大学测绘与地理信息学院，上海 200092)

目前常用的变形监测数据处理或分析方法主要有：回归分析、时间序列分析、传统灰色预测模型、神经网络和支持向量机等[1-5]，但是这些方法都有局限性。回归分析和时间序列分析适用于观测序列长、信息量大的数据[6]，但在实际工程中时常获得小样本数据，信息量小。传统灰色预测模型一般要求累加生成的序列具有灰指数规律并且是非负的[7]。神经网络存在着大样本、收敛速度慢和局部优化的缺点[8]。支持向量机存在如何选取合适的惩罚项、输出结果不具有概率意义等问题[9]。

高斯过程(Gaussian process，GP)对处理高维数、小样本、非线性等复杂问题具有很好的适应性，且泛化能力强[10]。苏国韵[11]和罗亦泳[12]分别将高斯过程应用于基坑位移时间序列分析和GPS高程转换，取得了较好的效果，从而验证了该方法的可靠性。目前通常采用共轭梯度法搜索超参数，存在对初始值依赖性强、容易陷入局部最优的缺点，该算法的适用性具有局限性[13-14]。人工鱼群算法(artificial fish swarm algorithm，AFSA)具有对初始值与参数选择不敏感的优点。笔者应用该算法对超参数进行智能寻优，建立AFSA-GP预测模型。利用该模型对等间距隧道位移和非等间距基坑沉降进行预测，以残差绝对值和与平均相对误差作为评价指标，选择神经网络(neural network，NN)、平方指数(squared exponential，SE)和有理二次型(rational quadratic，RQ)3种核函数分别进行预测，均具有较高的预测精度，其中以NN为核函数的模型预测效果最好。

1 模型建立

1.1 高斯过程原理

高斯过程是近期发展起来的一种新的机器学习方法，其对处理高维数、小样本、非线性等复杂问题具有很好的适应性。回归模型[10,15]可以表示为

y=f(x)+ε

(1)

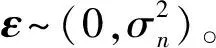
(2)

(3)

高斯过程中常用的核函数有NN、SE和RQ 3种核函数，其NN核函数一般形式为

(4)

SE核函数一般形式为

(5)

RQ核函数一般形式为

(6)

式(4)、式(5)和式(6)中，Q=diagl-2为超参数矩阵；l为样本数据点间的相关性；γ为核函数的形状参数。

利用传统共轭梯度法对偏导数进行最小化，从而获得最优超参数。负对数似然函数L(θ)和超参数θ的偏导数如下所示

(7)

(8)

1.2 AFSA-GP模型

针对共轭梯度法搜索超参数存在对初始值依赖性强、容易陷入局部最优的缺点，利用AFSA算法[16]代替传统共轭梯度法智能搜索最优超参数，建立AFSA-GP预测模型。主要步骤如下：

(1) 初始化AFSA算法中的参数，主要包括人工鱼数目、最大迭代次数、最大试探次数、视野范围、拥挤度因子和移动步长。然后随机产生初始人工鱼群。

(2) 利用高斯过程对样本进行训练和测试，根据食物浓度函数计算出当前每条人工鱼的食物浓度。

(3) 各人工鱼分别执行聚群行为和追尾行为，选择最有利的行为执行，缺省行为时执行觅食行为。

(4) 各人工鱼每试探一次，将自身食物浓度与最优食物浓度进行比较，若自身食物浓度比最优食物浓度更好，则用自身食物浓度代替最优食物浓度。

(5) 判断是否达到设定的最大迭代次数。如果已经达到最大迭代次数，则输出最优超参数。若未达到最大迭代次数，则迭代次数gen=gen+1，转到步骤(3)。

(6) 根据获取的最优超参数建立高斯过程模型进行预测。

2 实例分析

工程实例应用中采用了滚动预测方法[17]对变形体未来的形变量进行建模预测。AFSA-GP预测模型中采用了NN、SE和RQ 3种核函数分别进行计算，其目标函数(即食物浓度函数)设置为

(9)

式中，g(xi)第i个测试样本的预测值；yi为第i个测试样本的实测值；m为测试样本个数。

2.1 隧道变形监测的应用

依据文献[18]走马岗特长隧道采用分离式设计，建筑范围为14.75 m×5.0 m，最大埋深约为183 m。观测点YK21+715位于隧道出口右线上，选取其2012年6月连续18期周边位移数据作为试验数据，实测数据见表1。

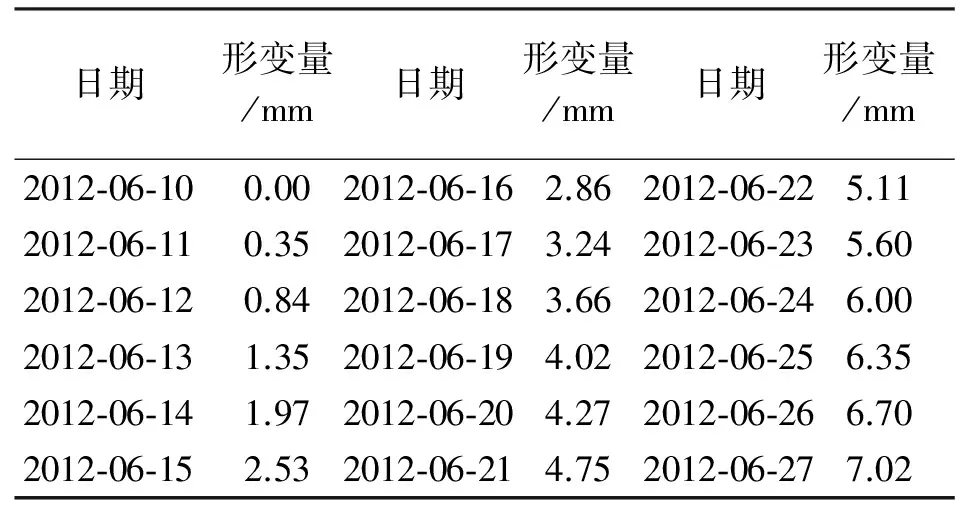
表1 监测点的各期实测数据

AFSA-GP预测模型中的参数初始化为：人工鱼数目为150，最大迭代次数为200，视野范围为5，移动步长为0.3。运用滚动预测方法进行预测时，k取13，P取10，t取1(即学习样本为10、测试样本数为3、预测期数为1)。GP核函数分别采用NN、SE和RQ核函数，目标函数为式(9)，求其最小值。利用AFSA-GP预测模型对隧道变形进行预测分析，目标函数值随迭代次数变化的曲线如图1所示，预测结果见表2，预测残差见表3，预测结果相对误差见表4。

图1 目标函数值随迭代次数变化的曲线

mm

表3 不同核函数的预测残差 mm

表4 不同核函数的预测结果相对误差 (%)

从表2、表3和表4可以看出，AFSA-GP预测模型的预测精度比GP预测模型有了很大的提高。AFSA-GP中残差绝对值和都小于1 mm，最大值为0.71 mm，而GP中最大值为2.20 mm。GP中最小相对误差为3.21%，AFSA-GP中仅为0.15%。NN、SE和RQ 3种核函数平均相对误差分别提高了3.26%、4.49%和3.35%，其中SE核函数提高最大。两种预测模型中NN核函数的预测精度高于SE、RQ核函数，表明NN核函数具有很好的预测能力。基于3种核函数预测的相对误差大于3%的，GP总计15个，而AFSA-GP只有2个。

从图1中目标函数值随迭代次数变化的曲线可以看出，AFSA-GP具有很好的预测精度，其中目标函数值的减小就是AFSA算法对GP超参数智能寻优的过程。目标函数值在迭代20—40次时基本处于稳定，迭代200次能够获得较为满意的工程应用要求。表3中的预测残差也表明AFSA优化GP超参数的有效性。

2.2 基坑变形监测的应用

依据文献[19]选取某基坑北侧边坡上监测点的观测数据作为试验数据，其非等间距实测数据见表5。

表5 监测点的实测值

AFSA-GP预测模型中的参数初始化为：人工鱼数目为150，最大迭代次数为200，视野范围为2.5，移动步长为0.3。运用滚动预测方法进行预测时，k取11，P取8，t取1(即学习样本为11、测试样本为3、预测期数为1)。GP核函数分别采用NN、SE和RQ核函数，目标函数为式(9)，求其最小值。利用AFSA-GP预测模型对基坑变形进行预测分析，目标函数值随迭代次数变化的曲线如图2所示，预测结果见表6，预测残差见表7，预测相对误差见表8。

从表6、表7和表8可以看出，AFSA-GP预测模型的预测精度比GP预测模型有了很大的提高。GP预测模型中残差绝对值和最大值为4.90 mm，而AFSA-GP预测模型仅为1.96 mm。NN、SE和RQ 3种核函数平均相对误差都有所提高，其中SE核函数提高最大，为3.38%。GP中最大相对误差为7.33%，AFSA-GP中仅为3.25%。两种预测模型中NN核函数的预测精度高于SE、RQ核函数，表明NN核函数具有很好的预测能力。基于3种核函数的预测相对误差大于3%的，GP总计4个，而AFSA-GP只有1个。

图2 目标函数值随迭代次数变化的曲线

mm

表7 不同核函数的预测残差 mm

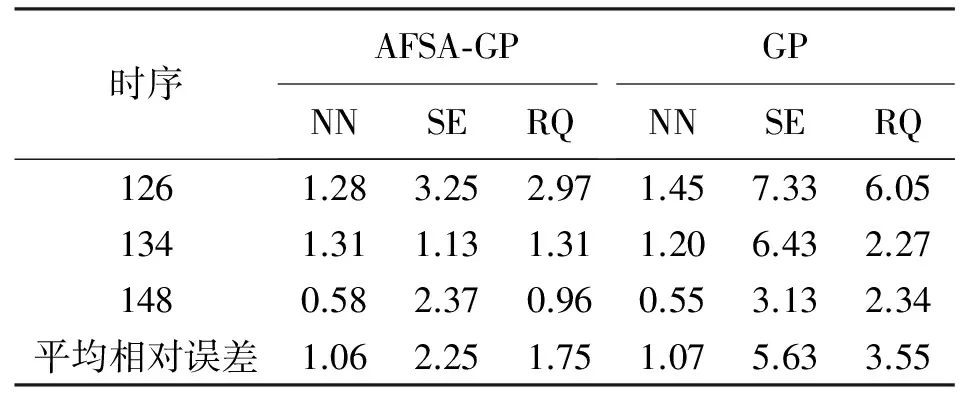
表8 不同核函数的预测相对误差 (%)

从图2中目标函数值随迭代次数变化的曲线可以看出，AFSA-GP具有很好的预测精度，其中目标函数值的减小就是AFSA算法对GP超参数智能寻优的过程。目标函数值在迭代20—40次时基本处于稳定，迭代200次能够获得较为满意的工程应用要求。表7中的预测残差也表明AFSA优化GP超参数的有效性。

3 结 论

(1) 人工鱼群算法具有对初值和参数选择不敏感的特点，利用人工鱼群算法代替传统共轭梯度法搜索最优超参数弥补了传统共轭梯度法的不足之处。两个工程实例残差绝对值和最大分别减小了1.49和2.94 mm，验证了该方法的有效性。

(2) 不同的核函数影响着机器的学习能力，对两种预测模型中3种核函数的预测精度进行比较，NN核函数预测精度最高，表明该核函数具有较好的外推预测能力。

(3) 将AFSA-GP模型应用于等间距隧道和非等间距基坑变形监测数据处理中，其中NN核函数预测的平均相对误差分别为0.69%和1.06%，表明该方法对等间距与非等间距变形监测数据处理均具有很好的适应性。

[1] 王卫东，何晖.回归分析在隧道拱顶沉降监测中的应用[J].科技信息，2011(7): 271-272.

[2] 袁金荣，赵福勇.基坑变形预测的时间序列分析[J].土木工程学报，2001，34(6):55-59.

[3] 潘国荣，王穗辉.深基坑事故隐患的灰色预测[J].同济大学学报(自然科学版)，1999，27(3):319-322.

[4] 陶津，刘燕，贺可强.神经网络在深基坑工程变形预测中的应用研究[J].青岛理工大学学报，2005，26(6): 39-42.

[5] 高永刚，岳建平，石杏喜.支持向量机在变形监测数据处理中的应用[J]. 水电自动化与大坝监测，2005，29(5):36-39.

[6] 李晓蕾，刘睿，田永瑞，等. 基于灰色预测的空间多点残差修正模型研究[J]. 大地测量与地球动力学，2010，30(5):125-128.

[7] 霍玉华. 隧道围岩变形量预测的灰色模型应用比较研究[J]. 北京交通大学学报，2006，30(4):42-45.

[8] 肖智旺，钟登华. 基于RBF神经网络算法的连拱隧道围岩变形预测方法研究[J]. 中国工程科学，2008，10(7):77-81.

[9] 熊志化，张继承，邵惠鹤. 基于高斯过程的软测量建模[J].系统仿真学报，2005，17(4):793-794，800.

[10] WILLIAMS C K,RASMUSSEN C E.Gaussian Processes for Regression[J]. Advances in Neural Information Processing Systems,1996,8(6)：514-520.

[11] 苏国韶，燕柳斌，张小飞，等. 基坑位移时间序列预测的高斯过程方法[J]. 广西大学学报(自然科学版)，2007，32(2):223-226.

[12] 罗亦泳，姚宜斌，张立亭，等. 基于高斯过程的GPS高程转换模型[J].测绘通报，2015(11)：11-14.

[13] 刘开云，方昱，刘保国，等. 隧道围岩变形预测的进化高斯过程回归模型[J]. 铁道学报，2011，33(12):101-106.

[14] 徐冲，刘保国，刘开云，等. 基于粒子群-高斯过程回归耦合算法的滑坡位移时序分析预测智能模型[J]. 岩土力学，2011，32(6):1669-1675.

[15] 何志昆，刘光斌，赵曦晶，等. 高斯过程回归方法综述[J]. 控制与决策，2013，28(8):1121-1129，1137.

[16] 李晓磊. 一种新型的智能优化方法——人工鱼群算法[D].杭州：浙江大学，2003.

[17] 刘开云，刘保国，徐冲. 基于遗传-组合核函数高斯过程回归算法的边坡非线性变形时序分析智能模型[J]. 岩石力学与工程学报，2009，28(10):2128-2134.

[18] 雷鸣. 基于高斯过程的变形预测算法研究[D].南昌：东华理工大学，2013.

[19] 尹晖，周晓庆，张晓鸣. 非等间距多点变形预测模型及其应用[J]. 测绘学报，2016，45(10):1140-1147.