木星系多目标探测轨道设计研究
张磊 田百义 周文艳 田岱 朱安文
(北京空间飞行器总体设计部,北京 100094)
木星系统作为太阳系内最大的行星系统,是深空探测的重要目标之一。通过对木星及其卫星系统的近距离探测,对于了解气态巨行星的起源和演化以及太阳系的发展具有重要意义。
国际上对木星系统的探测研究始于20世纪70年代,迄今为止,美国和欧洲针对木星系共进行了9次探测。早期以飞越探测为主,如先驱者10号、11号以及卡西尼-惠更斯号等[1]。后期逐渐转为环绕式探测,如1989年发射的伽利略号和2011年最新发射的朱诺号。作为首颗木星系环绕探测器,伽利略号对木星大气进行了原位测量,并对木星的4颗伽利略卫星(即木卫一、木卫二、木卫三、木卫四)进行了多次飞越观测[2],而朱诺号则在木星椭圆极轨道对木星深层大气、重力场、磁场以及磁球层等进行了全面观测[3]。除上述任务外,国外后续还规划了2次木星系探测计划,分别是欧洲的“木星冰卫探测”(JUICE)计划和美国的“快帆”计划,其中JUICE计划将重点针对木卫三进行环绕探测[4],“快帆”计划将重点针对木卫二进行多次飞越探测[5]。
作为我国2030年前深空探测的总体科学目标之一,统筹开展木星系探测将为完善我国深空探测科学研究体系,推动我国天文学等学科的发展和空间科技的进步发挥重要作用。木星系探测漫长的任务周期和较高的经费需求决定了顶层任务规划的重要性。我国首次开展木星系探测活动,要统筹科学需求与经济发展水平,高起点地开展深空探测活动,充分利用后发优势,争取一次任务完成木星及其卫星的多目标探测。考虑到木星系恶劣的空间辐射环境及探测器所携带的有限燃料等方面的限制,需对整个任务飞行策略进行研究及综合优化设计,寻找符合工程约束且总速度增量最优的任务轨道,实现科学探测价值的最大化。
根据上述需求,瞄准未来我国首个木星系及行星际穿越探测任务,本文结合木星系环绕探测任务目标、辐射环境、燃料消耗等方面约束,重点完成木星系多目标探测任务规划及转移轨道优化设计,为未来我国首次木星系环绕探测任务的工程实施提供有价值的参考。
1 任务目标分析
表1总结了目前国际上已发射和计划中的木星系环绕探测任务[6-7]。从表中结果可以看出,除朱诺任务外,国外已开展和规划中的木星系环绕探测任务均采用了低倾角大椭圆环木轨道,以实现对木星伽利略卫星的多次飞越,丰富探测科学目标。朱诺任务采用的环木极轨道虽然没有飞越木星的伽利略卫星,但能够实现对木星极区的多次飞掠探测。此外,JUICE任务除飞越木卫二、木卫三和木卫四之外,最终还计划实现对木卫三的环绕探测;而“快帆”任务则计划通过对木卫二的45次飞越,以达到对木卫二全方位探测的效果。

表1 国外木星系环绕探测任务概况
注:RJ表示木星半径,RJ=71 492.00 km。
根据国际上已有木星系环绕探测任务方案的特点,从任务方案科学性及探测方案先进性角度出发,未来我国木星系环绕探测任务除实现我国首次木星多圈环绕探测之外,可优先考虑实现如下几点探测目标:
(1)对木星极区的探测,增加对木星高能电子、木星磁场的起源和演化、木星极光形成等的科学认识;
(2)实现尽可能低的飞行高度,提升对木星表面结构、大气成分等方面的探测精度;
(3)实现对木卫四的环绕探测以及对其他伽利略卫星的飞越探测。由于木卫四处于比其他3颗伽利略卫星更弱的辐射环境,其地质后期演化也是最弱的,保存了更古老的地质信息,因此选取木卫四作为木星卫星系统探测的首选目标,而对木星其他伽利略卫星,尽可能实现多次飞越探测。
综合分析上述木星系探测任务目标,前两项目标要求环木轨道为大倾角、大偏心率的短周期轨道,而第3个目标则要求环木轨道倾角及偏心率不能过大。此外,为完成木卫四环绕探测目标,探测器在木星系内转移过程中需要利用木星伽利略卫星的多次飞越借力,以节省变轨燃料消耗。同时整个飞行过程还要考虑空间辐射环境、任务安全性、工程实现能力等方面的约束。因此,整个木星系内环绕探测任务轨道方案设计将极为复杂,需解决多目标约束下的飞行序列规划及转移轨道优化设计。
2 木星系内飞行方案选择
根据对2029-2033年间地木转移发射窗口及金星、地球、火星借力效果的分析,综合考虑探测器出发日期、运载发射能力、木星到达剩余速度、深空机动大小等约束,得到金星-地球-地球(VEE)借力序列在所考虑发射窗口下比金星-地球、金星-金星-地球等序列借力效果更佳。因此,本文以2029年9月25日发射窗口下探测器经金星-地球-地球3次飞越借力后到达木星的最优转移轨道为初值(见表2),开展木星系内飞行方案优化设计与分析。

表2 地木转移段轨道设计结果
根据第1节的分析,为实现对木星极区及木星表面结构的精细探测,要求环木轨道为大倾角、大偏心率的短周期轨道,而要实现对木卫四的环绕,又要求环木轨道倾角及偏心率不宜过大。此外,还要考虑空间辐射环境对轨道高度及轨道面方向的附加约束。由于不同目标对应的轨道约束彼此之间存在一定对立关系,同时兼顾工程实现上具有一定困难。因此需要在不同目标间进行折中或优选,如适当降低轨道倾角以兼顾对木星极区及木卫四的环绕探测,增加近木点高度以减小探测器所受辐射总剂量,或通过多次木卫四飞越代替环绕以保证对木星极区和表面结构的精细探测。为此,结合我国首次木星系环绕探测任务目标及工程约束,本文提出3种木星系内候选飞行方案。
(1)方案一:初始以较大轨道倾角和较低近木点高度完成木星捕获,并环绕木星飞行,以实现对木星极区观测以及对木星表面结构的近距离探测,之后利用伽利略卫星的引力辅助,转移至环绕木卫四轨道。
(2)方案二:初始以较小轨道倾角和较高近木点高度完成木星捕获,并环绕木星飞行,以降低探测器在木星系内运行所受辐射剂量,之后探测器同样利用伽利略卫星的引力辅助,转移至环绕木卫四轨道。
(3)方案三:初始以90°轨道倾角和较低近木点高度完成木星捕获,并环绕木星飞行,以实现对木星极区的飞掠探测以及对木星表面结构的近距离探测,之后探测器利用伽利略卫星的引力辅助,实现对木卫四的多次飞越探测。
3 木星系内飞行方案优化设计
根据引力辅助轨道动力学模型[8],利用改进的协作进化算法对木星系内引力辅助转移轨道进行优化。这里采用的协作进化算法综合了粒子群算法与差分进化算法的特点,通过共享二者种群最优解的方式进行协作寻优[9]。优化过程中,木星伽利略卫星的位置、速度矢量调用JUP230星历模型计算[10]。下面给出3种方案具体的优化设计结果。
3.1 方案一
(1)木星捕获:最后一次地球借力之后,通过1次深空机动,使得探测器到达木星时的近木点高度为4000 km,轨道倾角37.9°。当探测器飞至近木点4000 km处,通过1~2次近木点点火制动,被木星捕获为30天周期的环木大椭圆轨道。探测器深空机动与木星捕获所需速度增量为1.236 7 km/s。
(2)环木飞行:探测器在近木点4000 km、周期30天的环木轨道上开展木星探测,运行10圈,时间约300天。
(3)木卫四环绕探测:探测器完成对木星的观测之后,通过4次深空机动和2次木卫四借力,由初始环木大椭圆轨道转移至近木星四表面高度300 km、轨道周期17.7 h的环绕木卫四轨道。
表3和图1给出了探测器在木星系内轨道转移情况。
该方案变轨过程相对简单,且可同时实现对木星极区和木卫四的环绕探测。采用20 mm厚等效铝屏蔽层进行辐射防护,整个转移过程探测器所受总辐射剂量约为76.1 krad(Si)。
在该方案基础上,后续通过减小初始环木轨道周期可以增加探测器对木星的环绕探测圈数,不过总速度增量和辐射剂量会相应增加,应根据实际任务需求进行优化设计。
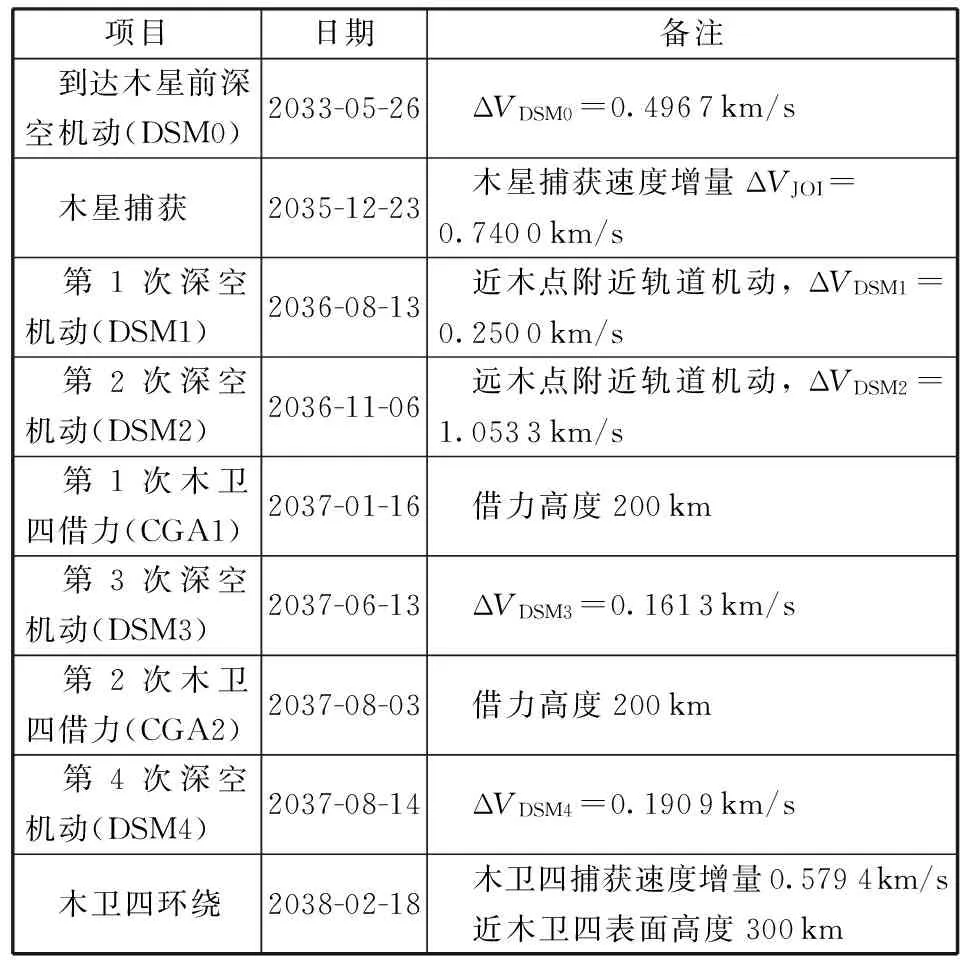
表3 方案一木星系内转移轨道参数

图1 方案一木星系内转移轨道Fig.1 Transfer trajectory in Jovian system of scheme one
3.2 方案二
(1)木星捕获:与方案一类似,探测器在最后一次地球借力之后,通过1次深空机动,使得探测器到达木星时的近木点高度为9.8RJ,轨道倾角2.1°。探测器到达近木点9.8RJ处,通过1~2次近木点点火制动,被木星捕获为204天周期的环木轨道。探测器深空机动与木星捕获所需速度增量为1.806 8 km/s。
(2)环木飞行及木卫四探测转移轨道:探测器被木星捕获后,通过2次木卫四借力和3次深空机动,进入近心点高度300 km、轨道周期17.7 h的环绕木卫四轨道,轨道转移过程中兼顾开展木星探测。通过优化设计,表4和图2给出了探测器转移轨道情况。
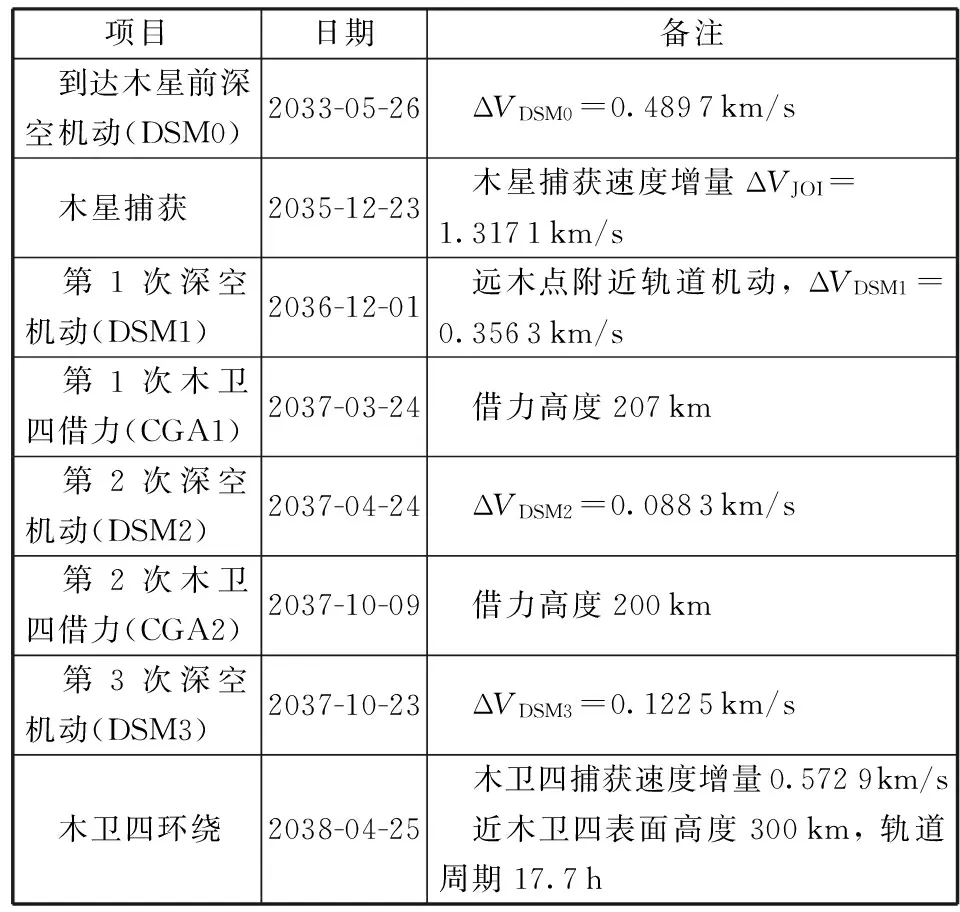
表4 方案2木星系内转移轨道参数

图2 方案二木星系内转移轨道Fig.2 Transfer trajectory in Jovian system of scheme two
该方案主要实现对木卫四的环绕探测,且由于近木点高度的提升,探测器所受总辐射剂量比方案一更少,采用20 mm厚等效铝屏蔽层进行防护,探测器所受总辐射剂量约为0.8 krad(Si)。不足之处是该方案环木轨道倾角较小,无法实现对木星极区的探测。
3.3 方案三
(1)木星捕获:在最后一次地球借力之后,通过一次深空机动,使得探测器到达木星时的近木点高度为4000 km,轨道倾角90°。当探测器到达近木点4000 km处时,通过1~2次近木点制动,被木星捕获为15天周期的环木轨道。探测器深空机动与木星捕获所需速度增量为1.332 8 km/s。
(2)环木飞行:探测器在轨道倾角90°、近木点4000 km、周期15天的环木轨道上运行10圈开展木星探测,时间约150天。
(3)多次木卫飞越探测:探测器完成环木探测任务后离开,开展多次木卫飞越探测,飞越顺序为:25次木卫四、次木卫三、次木卫二、次木卫一(木卫二、木卫一飞越根据探测器寿命情况拓展)。通过优化,表5和图3给出了探测器飞行轨道情况。
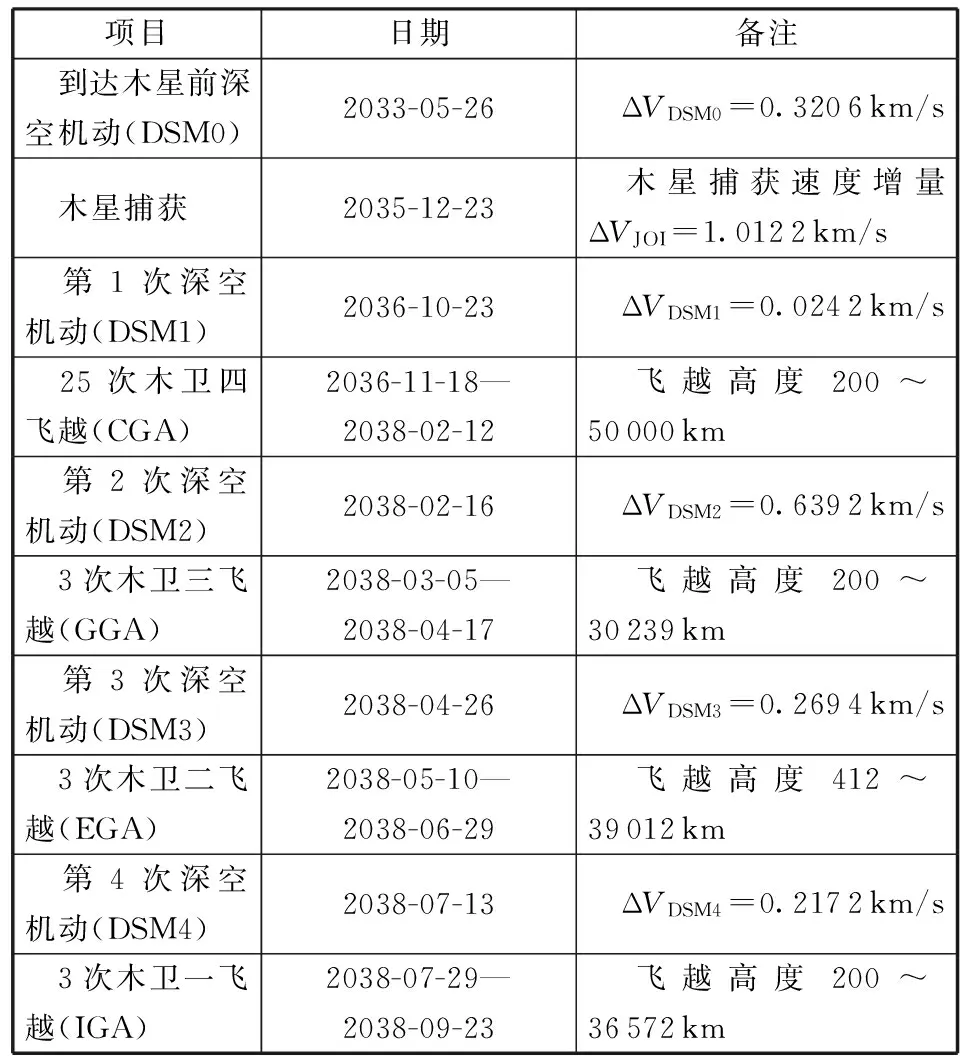
表5 方案3木星系内转移轨道参数
该方案可以实现对木星极区的多圈环绕探测,虽然没有完成对木卫四的环绕,但仅需消耗很小的速度增量,即可实现对木卫四的多次共振飞越探测(相邻两次共振飞越间的轨道修正大约在0.1 m/s量级,可以忽略不计)。采用20 mm厚等效铝屏蔽层进行防护,探测器在飞越木卫四、木卫三探测后所受总辐射剂量约为61.5 krad(Si)。如果进一步拓展对木卫二和木卫一的飞越探测,则总辐射剂量将增加至132.8 krad(Si)。
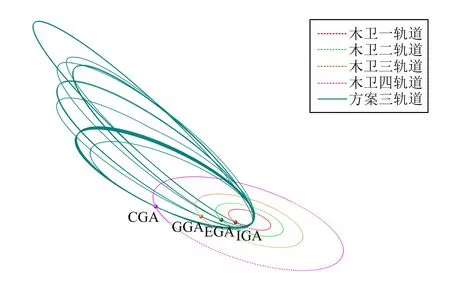
图3 方案三木星系内转移轨道Fig.3 Transfer trajectory in Jovian system of scheme three
3.4 方案对比分析
3种木星系内飞行方案及任务总速度增量对比见表6。由表可知:
(1)方案一可以同时满足对木星极区及木卫四的环绕探测要求,且近木点高度可以达到4000 km,能够实现对木星表面结构的精细探测。相比与JUICE任务,该方案轨道倾角更大,对木星大气的探测范围更广,且近木点高度更低。根据环木轨道周期选取的不同,有多种环木探测圈数可供选择(周期越短、环木圈数越多、总速度增量越大),是三种方案中的首选。
(2)方案二主要实现对木卫四的环绕探测,且由于探测器近木点高度的提高,总辐射剂量在3种方案中最小,不足之处是无法实现对木星极区及木星表面结构的精细探测。
(3)方案三可以同时达到朱诺任务和“快帆”任务的主要探测目标,既可以实现对木星极区的短周期环绕探测,又能够完成对伽利略卫星的多次飞越探测,且近木点高度也可以达到4000 km,满足木星表面精细探测的要求。虽然该方案最终没有实现对木卫四的环绕,但可以通过多次(25次以上)木卫四飞越探测代替。

表6 三种轨道设计方案比较
4 结束语
本文针对未来我国将要开展的木星系及行星际穿越探测任务,给出了3种木星系内多目标探测飞行方案。候选轨道设计方案均考虑了木星系辐射环境及工程实现等方面的约束。对于方案一和方案二给出的木卫四环绕探测轨道,后续可进一步利用木卫四共振飞越借力降低轨道周期,增加木卫四环绕探测圈数。此外,还可以利用木星伽利略卫星的借力制动,降低木星捕获的燃料消耗。关于单次任务同时实现木星近距离极轨环绕探测与木卫四环绕探测方案的可行性仍有待于进一步分析和优化。
References)
[1] 中国科学院月球与深空探测总体部. 月球与深空探测[M]. 广州:广东科技出版社. 2014:434-436
Lunar and Deep Space Exploration Department of Chinese Academy of Sciences. Lunar and deep space exploration[M]. Guangzhou: Guangdong Scienceand Technology Press,2014:434-436 (in Chinese)
[2] Michael Meltzer. Mission to Jupiter:a history of the Galileo project, NASA SP-2007-4231[R]. Washington D.C.:NASA, 2007
[3] T Kowalkowski,J Johannesen,T Lam. Launch period development for the Juno mission to Jupiter[C]// AIAA/AAS Astrodynamics Specialist Conference and Exhibit. Washington D.C.: AIAA, 2008:1-13
[4] The JUICE Science Study Team. JUICE exploring the emergence of habitable worlds around gas giants[R].Paris: ESA, 2011
[5] Brent Buffington. Trajectory design for the Europa clipper mission concept[C]// AIAA/AAS Astrodynamics Specialist Conference. Washington D.C.: AIAA, 2014
[6] 董捷, 孟林智, 赵洋, 等. 国外木星系环绕飞行任务规划研究[J]. 航天器工程,2015, 24(3):85-92
Dong Jie,Meng Linzhi, Zhao Yang, et al. Demonstration of foreign Jovian system orbiting mission plan[J]. Spacecraft Engineering,2015, 24(3):85-92 (in Chinese)
[7] Phillips C B. Europa clipper mission concept: exploring Jupiter’s ocean moon[J].Eos Transactions American Geophysical Union, 2014, 95(20): 165-167
[8] Matteo Ceriotti. Global optimization of multiple gravity assist trajectories[D]. Glasgow: University of Glasgow, 2010
[9] H Lei, B Xu, Y Sun. Earth-moon low energy trajectory optimization in the real system[J]. Advances in Space Research,2013, 51(5): 917-929
[10] Lainey V, Duriez L, Vienne A. New accurate ephemerides for the Galilean satellites of Jupiter:I, numerical integration of elaborated equations of motion[J]. Astronomy & Astrophysics, 2004,420(3): 1171-1183

