例析如何确定凸透镜的焦距
江苏省泰州市高港区教师发展中心(225323) 戴同兰
凸透镜成像规律是《光的折射》中的一个重要的知识点,也是在各种考试中经常出现的一个知识点。什么时候成实像,什么时候成虚像,什么时候像是放大的,什么时候像是缩小的,什么时候像是等大的,学生总是弄不清楚。特别是有的时候题目中不直接告诉学生凸透镜的焦距,要求学生根据题目中的隐含条件,结合凸透镜的有关知识,先求出凸透镜的焦距之后,再进行分析求解的题目,不少学生对此更是无从下手。本文结合平时常见的命题方式,整理出了求凸透镜焦距的几种方法。同时将实验室的凸透镜借给学生,要求学生在课后以小组为单位,通过综合实践活动的形式,利用这几种方法测出自己所借的凸透镜的焦距并进行交流,从而提高学生的动手能力。
1 平行光测焦距法
例1:(2017年湖南衡阳)在“探究凸透镜成像规律”的实验中:
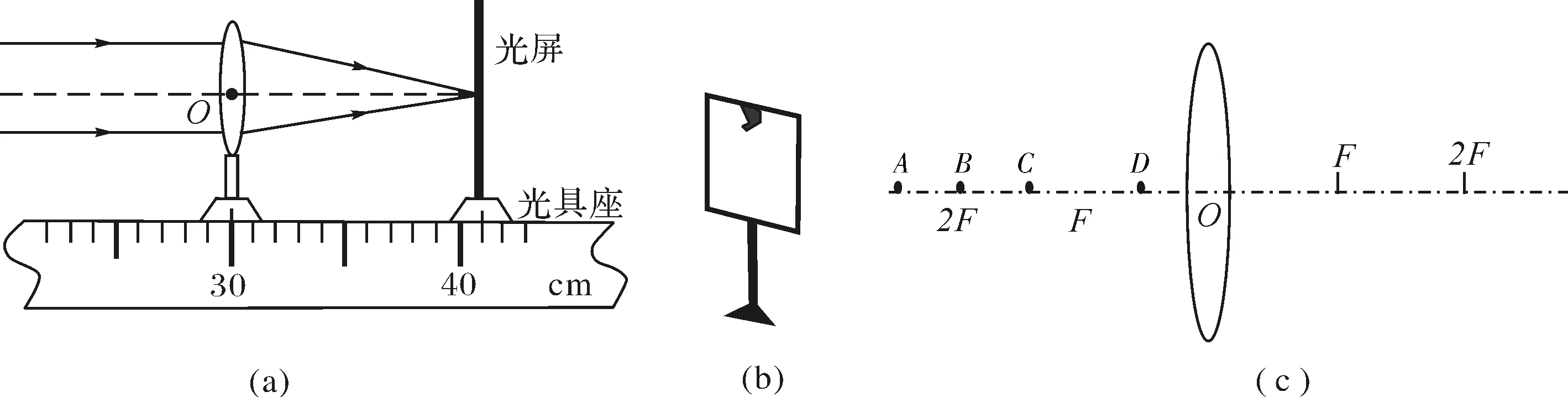
图1 探究凸透镜成像规律
(1)如图1(a)所示,该透镜焦距f=______cm。
(2)将蜡烛、凸透镜、光屏依次安装在光具座上后,点燃蜡烛,光屏上得到蜡烛的像如图1(b)所示。若要让像成在光屏的中心位置,则可以将凸透镜向______移动(选填“上”或“下”)。
(3)如图1(c)所示,把蜡烛放在光具座上_____点时 (选填 “A”、“B”、“C”或“D”);在光屏上能得到一个清晰放大的像,_____就是利用这种成像规律工作的 (选填 “投影仪”、“照相机 “或 “放大镜”)。
解析:(1)这道题目是粗略估测焦距的一种方法,通常也叫平行光测焦距法。其知识点是凸透镜能使平行于主光轴的光线会聚于一点,这个点叫焦点。要求学生知道焦距的概念是从焦点到光心的距离。本题中的光斑相当于焦点,所以从图1(a)中可知,该凸透镜的焦距是11.0 cm。
(2)要使像能成在光屏的中央,应使烛焰、光屏的中心大致在凸透镜的主光轴上。由图1(b)可知,光屏的位置偏高,所以要使像能成在光屏的中央,应将光屏向下调整。
(3)根据凸透镜成像规律可知,当物距在1倍焦距和2倍焦距之间时成倒立、放大的实像,其应用是投影仪。由图1(c)可知,C点在1倍焦距和2倍焦距之间,能成倒立、放的实像,其应用是投影仪。
故本题答案为:(1)11.0;(2)下;(3)C;投影仪。
2 10倍焦距测焦距法
例2:(2016年南通)在探究凸透镜成像规律时,小明将蜡烛沿主光轴由距透镜90 cm移至120 cm的过程中,发现烛焰在图2所示位置光屏上的像一直比较清晰。若他再将蜡烛移至距透镜7 cm处,移动光屏,则屏上得到的像一定是( )。
A.放大的像 B.等大的像
C.缩小的像 D.正立的像

图2 探究凸透镜所成的像实验
题析:这是估测凸透镜焦距的一种方法,有的地方把它归纳简称为10倍焦距测焦距法。
这种方法可能好多教师和学生在教学过程中都未关注到,所以学生在做到此类题目时无从下手。
根据该知识点可知估测凸透镜焦距的一种方法是:可使稍远处的窗户通过凸透镜在光屏上成清晰的像,这时光屏与凸透镜的距离就近似等于凸透镜的焦距。
同样根据该知识点也可以很快的判断出题目中凸透镜的焦距是5 cm,将蜡烛移至距透镜7 cm处,此时物距在1倍焦距和2倍焦距之间时成倒立、放大的实像,故本题答案为:选A。
上述两种测焦距的方法实质是一样的,平行光测焦距法可以把物距看成是在无穷远处,根据凸透镜成像公式当物距趋向于无穷大时,趋向于0,则v≈f。当物距大于10倍焦距时,也可以认为趋向于0。
3 2倍焦距测焦距法
例3:如图3所示,李宁同学在张老师的指导下完成“探究凸透镜成像规律”的实验。

图3 凸透镜成像实验
(1)当蜡烛位于图3中B处时,移动光屏到D处,观察到光屏上呈现清晰的像,此时像和物大小相等,则该凸透镜焦距为______cm。
(2)李宁同学把蜡烛移动到A处,屏上的像变得模糊,要使像变清晰,光屏应向______(选填“左”或“右”)适当移动,此时光屏上的像应该是倒立、_____的实像。
(3)在上述(2)操作的基础上,张老师取下自己戴的眼镜放于蜡烛和凸透镜之间、光屏上的像又变得模糊,李宁同学发现当光屏向左移动适当距离后像又清晰。由此可知,张老师所戴的眼镜是______,张老师的眼睛属于______(选填“近视镜”、“远视眼”、或“正常眼”)。
解析:(1)根据凸透镜成像规律可知,当物距u等于两倍焦距时,利用凸透镜成倒立、等大的实像,此时像距v也等于两倍焦距。由图中信息结合像距与物距的关系可知,u=v=20.0 cm,则2f=20.0 cm,f=10.0 cm。
(2)根据物近像远像变大的特点分析,当把蜡烛移动到A处,物距变大,像距变小,所以应将光屏靠近透镜,向左移动;此时物距大于2f,所以在光屏上成倒立、缩小的实像。
(3)根据像的位置变化判断眼镜对光线的作用,进一步判断出眼镜的种类.把眼镜放于蜡烛和凸透镜之间,光屏向左移动适当距离后像又清晰。说明该眼镜对光线具有会聚作用,为凸透镜,是远视眼镜。
故本题答案为:(1)10.0;(2)左;缩小;(3)凸透镜;远视眼。
4 焦点不成像法
例4:在探究凸透镜成像规律的实验中,无论怎样移动光屏,光屏上始终得到一个大小不变的圆形光斑。其原因是什么?
这一题目是根据光的折射中光路可逆,我们知道:从焦点发出的光经过凸透镜后平行于主光轴射出,这就是我们通常所说的当物距等于焦距时,凸透镜不成像,也有一种说法是像成在无穷远处,我把它归纳简称为焦点不成像法。本题中光屏上始终得到一个大小不变的圆形光斑,说明光经过凸透镜后是平行射出的,那么光源位于凸透镜的焦点处,此时如果题目中给出光源到凸透镜的距离,也就相当于告诉了我们凸透镜的焦距。故本题答案为:光源位于凸透镜的焦点处或物距等于焦距。
当然也有时候反过来考,如在探究凸透镜成像规律的实验中,当光源位于凸透镜的焦点处时,移动光屏过程中,光屏上有什么现象?答案是:光屏上始终得到一个大小不变的圆形光斑。

