基于改进型Duffing 混沌方程的微弱信号检测方法

王威威 沈超

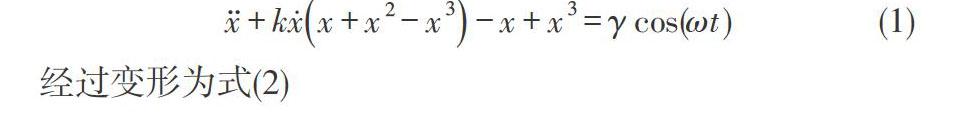
摘要：研究了一种利用Duffing 方程混沌特性检测微弱信号的方法，通过改变系统状态-由混沌态转变为周期态来检测微弱信号的存在，相图显示出混沌系统对强噪声背景的免疫性和对微弱信号的敏感性。实验结果表明对于不同的混沌信号输入，系统会产生不同的相图输出结果，因而可有效地检测到微弱信号的存在。

关键词：Duffing方程;微弱信号检测;混沌;信噪比;相轨迹图

中图分类号：TN911.23        文献标识码：A        文章编号：1009-3044（2018）35-0238-06

Abstract：An  approach to detecting the weak signal by using Duffing equation is studied. The existence of weak signal is detected by changing the chaotic state to the periodic state. The phrase image shows the immunity of the chaotic system to strong noise and sensitivity of the weak signal. It shows that in the case of different chaotic signal input， the system produces different image output results， which can effectively detect the existence of weak signals.

Key words：Duffing equation;  weak signal detection;  chaos;  SNR; phase trajectory

1 背景

微弱信号检测技术在生物医学、振动测量、通信以及电力系统故障诊断等领域具有广泛的应用背景，一直是国内外学者研究的热点和难点问题。近年来微弱信号的检测成为混沌领域越来越关注的重点，特别是强噪声背景下的微弱信号检测技术在通信、雷达等工程领域产生了重要的作用。当微弱信号强度非常小时，很容易被环境中存在的强噪声所干扰，使对其地检测变得非常困难。目前，研究发现Duffing方程对特定的频率的信号具有强烈的敏感性，而对随机的噪声信号具有免疫特性，故因此在微弱信号检测领域Duffing方程发挥着重要的作用。

2 研究原理

2.1 Duffing方程形式

众所周知，动力学系统中有很多能够产生混沌吸引子，比如常见的Lorenz方程，Rossler方程，Duffing方程等，其中Duffing方程是非线性系统中研究比较广泛的数学模型，因此我们用Dufifng方程来构造强噪声背景下的混沌检测系统，改进的Duffing的混沌系统的形式如下：

经过变形为式（2）

其中系数k为阻尼比，[-x+x3]为非线性恢复力，[γcos（ωt）]为周期策动力。

2.2 系统特性

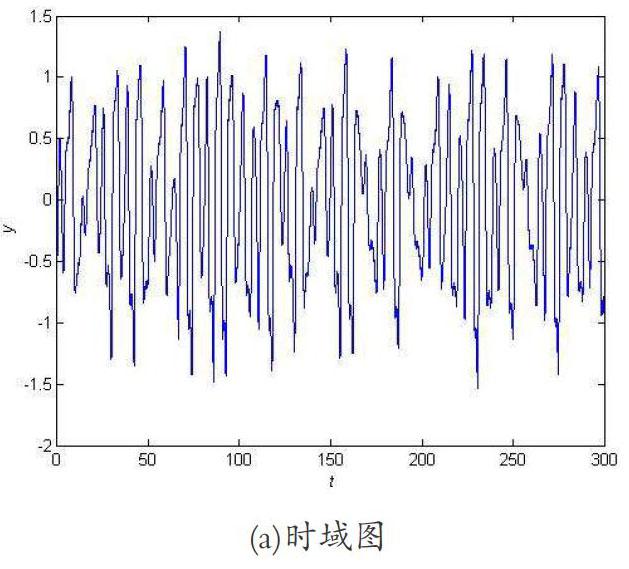
在系统（2）中当k取固定值 0.5时，研究系统的混沌特性，当策动力幅值[γ]=0时，发现系统存在三个平衡点x =0，x=1，x=-1。采用Matlab仿真，当平衡点为x=0时，系统的时域图和相轨迹为图1所示，当平衡点为x =1，x=-1时，相轨迹图为围绕平衡点的涡卷图及时域图如图1和图2所示。

当[γ]>0 时，系统表现出复杂的动力学形态，具体又可分为以下几种情况：[γ]较小时，轨迹表现为 Poincare 映射意义下的吸引子，点围绕焦点作周期振荡，渐增加到临界值[γc]时，随着[γ]的增大，系统历经同宿轨道、周期分叉直至达到混沌状态。这一过程随着[γ]的变化非常迅速。Duffing 振子各个状态的时域波形及相平面轨迹如图 4～图 6 所示。

[γ]在很长時间内，系统都将处于混沌运动状态。进一步增加超过阈值[γd]，系统进行大尺度周期振荡（如图 7）。此时相轨迹将焦点、鞍点团团围住，对应的庞加莱映射亦为不动点。

整体上看发现当[γ]由零逐渐增大，系统相图轨迹状态呈现有规律的变化：系统由分岔轨迹、混沌轨迹、大尺度周期状态切换。

3  微弱信号检测方法和性能分析

3.1 微弱信号检测

从对 Duffing 混沌振子随策动力幅值变化其运动形式随之变化的规律分析，可以利用相轨迹由周期振荡到混沌运动或由混沌运动到周期振荡的显著变化来检测信号，这种变化对策动力幅值的敏感性及对噪声的免疫力是其可以用来进行微弱信号检测的基础。

微弱正弦信号混沌检测原理：我们首先调节系统策动力幅值[γ]，取[γ=γd] ，使系统处于从混沌状态向大尺度周期状态过渡的临界状态。当用小幅值的、与周期策动力频率相近的余弦信号以及白噪声对 Duffing 混沌振子进行摄动时，系统将从混沌运动状态进入大尺度周期运动状态，通过在计算机上观测混沌系统相轨迹变化，得知待检信号中是否含有所要检测的正弦信号。此时，只要继续调节策动力幅值[γ]，使得系统再一次处于混沌到大尺度周期的临界状态，此时的策动力幅值[γd′]，可求得待测信号的幅值为[a=γd-γd′]。之所以选择系统从混沌运动状态进入大尺度周期运动的状态变化作为检测的临界点，要是基于两点原因：一是因为从混沌状态进入大尺度周期运动时系统在相平面上的轨迹将产生很明显的变化，以便我们辨识系统的变化;另外一点是因为此时外界强噪声对于系统的影响是最微弱的。

微弱信号检测系统方程为

其中[fcos（ωt）]为输入的微弱信号，[n（t）=σε（t）]为高斯白噪声信号。

当[γ=0.6798]，k=0.5，[σ]=0时，系统的输入待检测信号前后的相图为图8所示。

由图8看出在高斯白噪声的前提下，在未存在微弱信号前提下系统处在临界混沌态，添加微弱的余弦信号后系统立即变为周期态，从而可以判断出系统存在微弱信号。

为了检测出周期信号幅度的大小，计算机在计算过程中，循环一次，自动地将策动力的幅值[γ]减少 0.0001，直到统由周期状态变为混沌状态。此时[γ]减少为0.6798。于是，以求出幅值[a=γd-γd′]（[γd]为临界的周期态策动力幅值，[γd′]为临界的混沌态策动力幅值），得到这个结果与真实值[a]相比，存在一定误差，原因是因为我们难以确定精确的[γd]的值。

3.2 性能分析对比

3.1.1 信噪比分析

为测试系统的抗噪声能力，输出高斯白噪声经过仿真后如图所示：令式（3）中[σ≠0]时，分析在不同的噪声强度背景下系统相图的变化。

（b）相平面轨迹

观察图9-图11的变化，可以看出在一定的噪声强度下，系统相图混沌态基本不变，说明经改进后的Duffing方程保持着良好的抗噪性。

添加微弱信号，检测系统在检测微弱信号时的抗噪声能力。令[γ=0.6798]，使系统处于临界状态，添加不同噪声强度观察如图所示：

当外部噪声信号的幅值[σ]从0增加到0.04时，系统的检测微弱信号的状态并不受噪声强度的影响，展示了系统的强大的抗噪声的能力。当噪声幅值[σ]增加到0.05时，系统检测效果下降，微弱信号检测效果不明显，如图13所示。实验结果表明当噪声信号幅值小于0.04时，系统是稳定可靠的，因此系统的信噪比为如下：

实验结果显示，该混沌系统具有较好的抗噪声能力。

3.2.2 不同微弱信号频率分析

当添加待检测的外部的微弱信号和策动力参考频率不同时，对于[ω1]取0.5，1.5，3，10等仿真，发现对于接近策动力频率的微弱信号有一定的检测效果，但效果不明显，当与策动力频率相差较大时，系统相图状态没有发生变化，仍然保持混沌状态。故改进后的Duffing方程对于与策动力频率相同时的待测信号效果最好。

经与之前的Duffing方程对比，该改进后的Duffing方程的优点主要体现自两个方面：一是系统在信噪比方面得到提升，目前采用时域方法处理信号的最低信噪比门限只有-10dB，并且与其他的改进的Duffing方程[9]对比发现，信噪比有一定提升，有良好抗噪声性能。二是系统在检测微弱信号的量级上有较好的提高，在常见的Duffing方程中检测微弱余弦信号的幅值一般为0.01，而此论文中系统的检测信号幅值为0.0001，说明系统在混沌态和周期态的过渡期更短，较好地提高检测微弱信号的精度。

3.3 方法存在的问题及改进方向

Duffing 振子微弱信号检测方法是一种时域信号处理技术，但仍存在很多难题亟待解决。其中一个突出的问题是：检测系统在混沌态和周期态的临界状态下，我们采用的自增步长的方式改变策动力幅值，由于精度的原因，容易出现误判。且随着检测精度的提高， 状态转换过渡过程不明显， 而检测时间长短，只能通过反复的实验数据进行估计，因此系统可能会发生误判。因此，研究解决减小过渡过程的影响，提高 Duffing 振子混沌检测系统的实时性具有重要意义。

Duffing振子信号检测方法中还存在两个方面的问题：一是通过混沌向大周期的转化进行同频信号检测时存在检测盲区;二是利用状态转化来进行信号检测时主要停留在定性分析上，这主要是指通过观察时域序列图和相图等方式进行系统所处状态的判决。

为了能更有效地实现基于 Duffing 振子的微弱周期信号检测，还要重点从混沌区间保持性，混沌系统临界点相图的状态的突变性以及临界相变的容噪性能等方面做进一步研究，目前这些方面的研究鲜有文献述及。研究混沌系统的这些检测性能可以针对检测要求更好地选择不同的混沌振子，对基于 Duffing 振子的微弱信号混沌检测的工程应用具有重要的实际意义。

4  结论

文中研究了改进过Duffing混沌方程系统在微弱信号检测领域的方法，讨论如何利用Duffing方程特性对微弱信号检测的原理，给出具体的仿真图像，显示出系统由混沌态向周期态转变的过程。举出微弱信号检测的实例显示出检测的效果是明显的和有效的。信噪比达到了-52dB，显示出系统在噪声情况下的稳定。指出了Duffing方程检测信号存在的问题，我们还需要大量的研究去分析性能特性，以解决存在的精度和准确度问题。但从总体看，基于改进的Duffing方程的微弱信号检测仍具有较好的效果。

参考文献：

[1] L.B. Donald. Chaotic oscillators and CMFFNS for signal detection in noise environment[J]. Proceedings of the IEEE International Joint Conference on Neural Networks， Baltimore， MD， Vol. 2， 1992， pp. 881-888.

[2] B.B. Okolewska， K. Czolczynski， T. Kapitaniak， J. Wojewoda. Chaotic Mechanics in Systems with Impacts and Friction World Scientific[J].Singapore， 1999.

[3] Vimal Shah， Wallace Gardner， Don H Johnson， Sinan Sinanovic.Design Considerations for a New High Data Rate LWD Acoustic Telemetry System[R]. SPE 88636 2004：1-7.

[4] Li Y， Yang BJ， Yuan Y， Liu XH. Analysis of a kind of Duffing oscillator system used to detect weak signals[J].Chin Phys 2007;16（4）：1072-6.

[5] Zhao WL， Zhao JX， Huang ZQ， Meng QH. Weak signal detection technology Based on holmes Duffing oscillator[J].Procedia Eng 2012;29：1796-802.

[6] Choe C U， Hohne K and Benner H.2006 Phys[R].Rev. 72362.

[7] 呂金虎.陆君安混沌时间序列分析及其应用[M].武汉武汉大学出版社，2002.

[8] 谢红梅.基于混沌理论的信号处理方法研究[D].西安：西北工业大学，2003.

[9] Zhao Zhihong，Yang Shaopu. Application of van der Pol—Duffing oscillator in weak signal detection[J].Computers and Electrical Engineering 41 （2015） 1-8.

[通联编辑：唐一东]