含非线性二极管电路的等效分析法

吕桃

摘 要 探讨含非线性二极管中假定状态、戴维南定理的运用，以寻求和破解有关复杂非线性二极管电路的分析、计算方法。

关键词 非线性二极管；戴维南定理；线性电路

中图分类号：G718.3 文献标识码：B

文章编号：1671-489X（2018）01-0070-03

1 前言

电路理论分析中，中等职业学校学生一般对于线性电路的认知相对比较清晰，但对于诸如含二极管这类非线性器件电路的学习，理解和掌握就较困难。在教学中，除了学生对非线性元器件认识不足因素外，还有两点主要因素：1）未能掌握或者说未系统地掌握根据非线性元件特性进行应用的相关特殊方法；2）难以将部分线性电路的定理、方法迁移至含非线性器件的电路。

这几方面因素不解决，就达不到预期的教学目的，除对本课程教学效果造成影响外，学生在学习复杂的模/数电电路含非线性器件的复杂电路时，会更加难以理解。

文章针对应用广泛的非线性器件二极管，结合长期教学与探索的经验，探讨如何正确运用戴维南定理与教会学生利用假定状态分析方法解决此类问题。

2 正确理解二极管等效模型是掌握分析方法的前提

二极管电路分析一般基于二极管单向导电的重要特性及由此建立的电路等效模型，分析中常采用的模型有三种。

1）理想模型：该模型反映二极管正偏导通、反偏截止的纯开关特性，主要用于线路分析和近似计算，突出开关控制功能。

2）恒压降模型：采用沿正向极性恒压源串联理想模型形式，常用于一般性要求的分析计算，强调其导通电压的基本不变性质。

3）小信号模型：在较为精确的电路分析计算中，可反映出器件动态电阻、两端电压和电流的函数变化。

另外还有一种折线模型，介于恒压降模型与小信号模型之间[1]。

实际分析中若无特殊要求或说明常采用恒压降模型，硅管Uon取0.7 V。

3 二极管电路分析利器——戴维南定理

戴维南定理是线性电路非常重要的定理，是一个进行电路分析的重要工具。戴维南定理可用来：1）求解某一未知支路中电流或两端电压；2）分析电路中某元件性能或参数发生变化带来的影响；3）分析和计算含诸如二极管类非线性器件的电路。

针对上述前两类线性电路分析、计算的方法较易掌握，而对于第三类含非线性元件电路，运用戴维南定理时常摸不着头绪。下面结合实例，分析运用戴维南定理解决此类问题的方法。

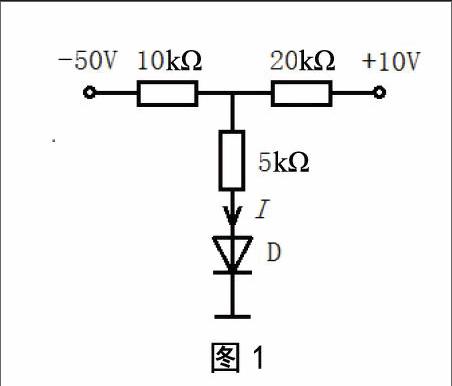
【题例】试求图1所示电路中非线性硅二极管中通过的电流I。

【分析】本题中在确定二极管中电流大小时，首先要确定二极管的工作状态。解题思路是通过等效变换，将电路转化成含二极管的单回路电路，从而判断二极管工作状态，进而确定工作电流。

本题按戴维南定理求解某一支路电流的标准解题流程，第一步从二极管两端断开后，求出极性与待求电流方向一致的二端开路电压，UOC=-30 V；第二步求出二端电路的戴维南等效电源内阻，RO≈11.67 kΩ；第三步画出电动势为

-30 V、等效内阻为11.67 kΩ的二端等效电源，将二极管对应接回端钮位置，显然二极管承受反向电压，故二极反向截止I≈0。

【题例】若将上题电路中的二极管颠倒方向反过来接于原位置，求流过二极管电流I。

【分析】求解与分析方法同上，且求解过程的前两步完全相同，只是第三步二极管接入的极性与前面不同，接入后显然二极管承受的是正向电压处于导通状态。导通电流的求解需结合恒压源模型，通过计算与其串联的线性元件电阻电流，达到求解二极管电流的目的。利用UOn=0.7 V，等效内阻两端电压UR=30-0.7=29.3 V，则电流大小I=UR/RO≈2.5 mA，与参考电流方向相反。

综上，运用戴维南定理分析含二极管电路分析方法：

1）从二极管两端断开原回路，求二端含源部分的戴维南等效电源；

2）将二极管接入等效电源开路间，结合等效电源极性判断二极管的导通、截止状态；

3）在导通情况下利用恒压源模型确定等效内阻压降，并通过求电阻电流确定二极管通过的电流（尽管已知二极管伏安特性表达式ID=IS（eqU/KT-1），但一般要求的场合很少采用）[2]。

上述方法显然适宜针对含单只二极管电路或多只二极管的串联电路。

4 合理采用假定状态分析方法是进行分析特别是复杂电路分析的正确保障

电子电路中，特别是数字逻辑电路较多的涉及若干只二极管的非单支路连接，较好的办法是根据电路工作状态转化成符合上述特征进行求解分析。关键仍是利用戴维南定理在电路分析中实现多个二极管状态的判断，以确定其中某一个二极管导通或全部截止，最终确定电流。其中对于多只二极管工作状态的判断是基于一种假定状态的分析方法，先假定二极管处于导通或截止状态，然后根据这一假设对电路进行分析计算，判断所得结果与假定状态的参数是否一致，若一致则假设成立，否则应另行假设再重复进行。

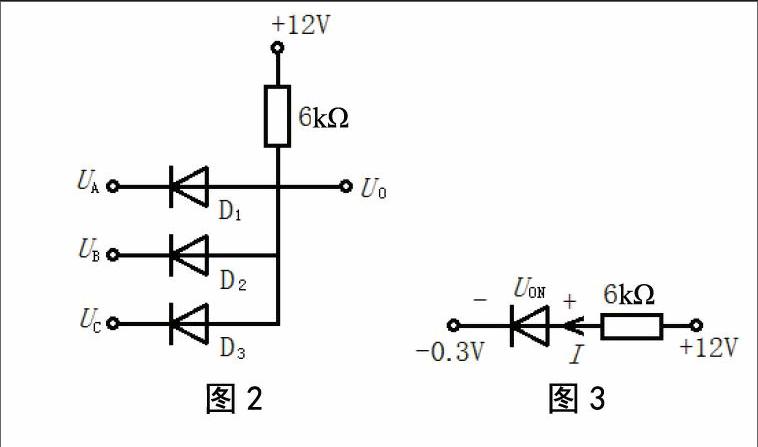
假定状态中，电路中含N只二极管，则可能的电路状态组合数是2N个。但通常某些状态组合是很容易判定为不合理的，也就可以大大地缩小假设的状态组合范围。以数字电路中常见的“与门”电路为例进行说明。图2所示三输入与门电路：输入信号UA=3.5 V，UB=0.3 V，UC=-0.3 V，判定输出UO和电源输出电流I。显然，结合数字电路的开关特性要求，分析中宜采用二极管的理想模型。

初识电路图，乍一看，易产生三只同向接法的二极管均可导通的误判，原因是每只二极管阳极均通过6 kΩ电阻接12 V电源正极，这一电位比任一只二极管的阴极电位都高。用假定状态法来排除，即假设三只二极管均处于导通状态，结合理想模型则三只二极管开关接通状态视作短接。此时每只二極管的阴极不可能分别保持UA=3.5 V、UB=0.3 V、UC=-0.3 V的对地电压值，应全部相等。显然与实际条件不符，故绝没有可能全部导通。同理也可排除两只二极管同时导通的可能性。endprint

剩下只有一个二极管导通的可能性，设想谁最有可能导通呢？显然取决于哪一只二极管正偏电压降最大。管子C输入负电位最低，由此假定管C导通，管A、管B截止。管C导通时因UC=-0.3 V，有UO=-0.3 V，管A、管B此时均承受反偏电压满足截止条件，与假设吻合。

分析中若没有考虑到管子两端电压降大小问题，做出管B导通，管A、管C截止的假设，管B导通时由于UB=0.3 V，

有UO=0.3 V，管A处于反向偏置，满足截止条件，管C则满足正向导通条件，假设不成立。假设A导通的分析推理相同。

上述分析中也可采用恒压降模型，所不同的是管C导通时输出电压为：UO=-0.3 V+0.6 V=0.3 V。不管采用何种二极管模型，分析时需兼顾二极管死区电压的影响。在进行形同与门、或门电路的有多只二极管同向接于公共点的二极管电路分析时，结合上述分析不难找出相应的规律：优先假定接于公共点的正向压降最大的二极管导通，据此决定输出（公共点）电位，再判定各只二极管的状态是否符合假设[3]。

本例中确定管C导通后，将截止状态元件管A、管B支路舍去，可畫出图3所示等效电路，直接利用电阻R两端电压降确定二极管或电源输出电流。

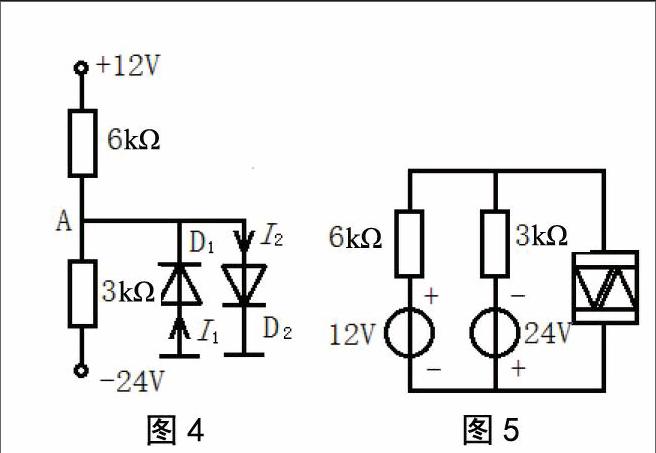
在学习中常会遇到与上述特征不吻合的电路，模拟电路中此类现象较普遍，这类二极管状态、电流如何求解？试求图4所示电路中两只二极管中通过的电流I1、I2。

【分析】因A点电位未知，两只二极管有四种可能工作状态组合，即：D1和D2导通；D1和D2截止；D1导通，D2截止；D1截止，D2导通。

进一步分析可发现：两只二极管反向且均有一端接地，故全导通、全截止不可能，仅存在后两种可能性。究竟D1还是D2导通，可以进一步采用假定状态分两种情况分析，即某一二极管导通后，VA电位由恒压降模型确定，则电阻6 kΩ和3 kΩ中的电流方向也就确定了；导通二极管电流方向唯一，不能改变，结合节点电流定律验证“假定”成立与否。

采用戴维南定理分析、计算，更能体现解决问题方法的缜密性。上述推论已知两只二极管中仅能有一只导通，将两只反向并接的二极管视作一条“双向二极管”支路，将简化电路还原回路，画法如图5所示。

等效电源端钮处电压参考极性习惯取上“+”下“-”，有等效电压US=UOC=-12 V，戴维南等效内阻RO=6 kΩ//3 kΩ=

2 kΩ。

显然，等效负载支路承受上“-”下“+”电压极性，由D2截止、D1导通，可将D2开路去路擦除，保留导通的D1，采用理想二极管模型：

I1=IR=12 V/2 kΩ=6 mA I2=0

若采用恒压降模型，则：

I1=IR=（12 V-0.7 V）/2 kΩ=5.65 mA

5 结语

综上所述，对于应用广泛的含非线性二极管电路，有机地将假定状态分析法与戴维南定理两者结合运用，是此类电路分析、计算走出困惑，使问题简单化、思路趋于清晰有效方法[4]。

参考文献

[1]李树雄.电路基础与模拟电子技术[M].1版.北京：北京航空航天大学出版社，2000.

[2]李翰荪.电路分析基础[M].2版.北京：高等教育出版社，1983.

[3]周绍敏.电工基础[M].1版.北京：高等教育出版社，2001.

[4]余孟尝.数字电子技术基础简明教程[M].2版.北京：高等教育出版社，1999.endprint