静态全符号网络的社群结构

何晓晨,杜海峰,杜巍,费尔德曼

(西安交通大学公共管理与复杂性科学研究中心,710049,西安)

社群结构作为复杂网络科学研究的重点,揭示了个体间的关系与网络的组织结构,有效诠释了社会生活中“人以类聚”的特性[1-3]。全符号网络的社群结构则是在原有社群结构研究的基础上同时考虑节点属性与边的属性,可以有效反映出集群行为的发生机制与演化特征,对于缓解群体矛盾与预防恶性群体性事件等国家公共安全问题具有重要意义。

Newman等人于2002年首先提出社群结构的概念,即网络中社群内节点关系稠密,社群间节点关系稀疏,同时给出了模块度指标,用于反映社群结构特征的明显程度[3]。然而,该指标只针对0-1网络,忽略了网络的边和节点的属性。考虑了边属性的网络被称为符号网络,对于个体聚类分析具有重要作用[4]。在符号网络的分析中,结构平衡理论从关系层面解释了网络中个体的聚集过程,受到学者的广泛关注[5-8]。依据平衡理论,Gmez等人于2009年基于结构平衡理论在原始的模块度函数上进行了改进,并以改进后的模块性函数作为衡量符号网络社群结构的指标[9]。节点属性是社会网络的重要特征,对于个体聚集同样起到基础性的作用[10-14]。在将模块度引入符号网络的同时,将节点属性纳入到社群结构分析中,可以更全面地分析网络的社群结构特征。Du等人将节点属性引入一般符号网络中,构造了带有节点属性的全符号网络,而该网络事实上具有更重要的社会学意义[15]。李树茁、任义科等人将2005年深圳市农民工调查的关系数据与个体属性数据进行了结合,构造了农民工的全符号网络数据,并利用该数据对农民工的特定行为进行了分析[16-17]。这些研究不仅丰富了传统的实证研究方法,也拓宽了网络科学在社会科学当中的应用。本文将在全符号网络体系中提出社群结构的概念,并构建相应指标。该指标将网络结构、关系与节点属性综合考虑,以期为个体的聚类提供新的方法和路径。

1 全符号网络下的社群结构指标

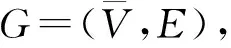
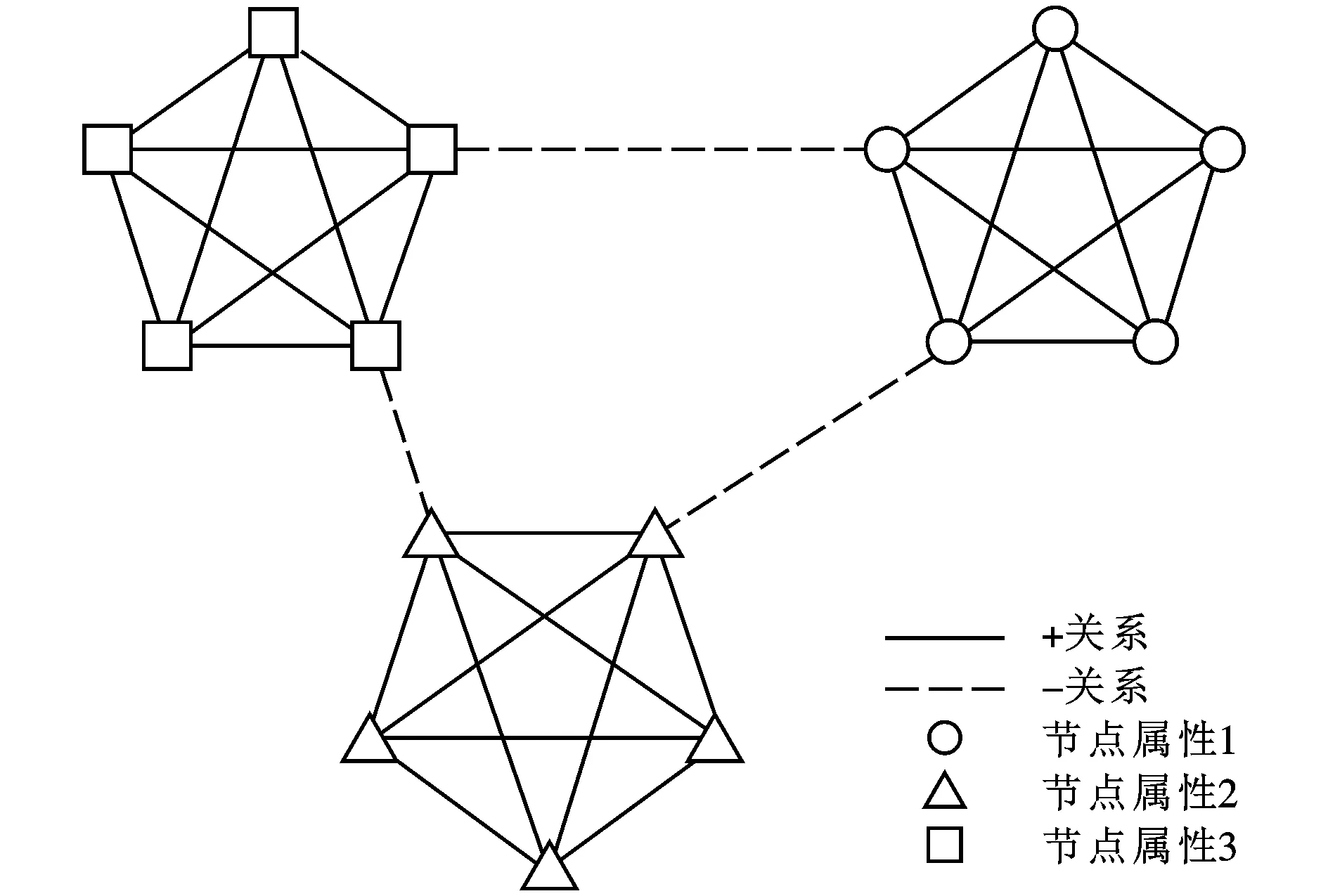
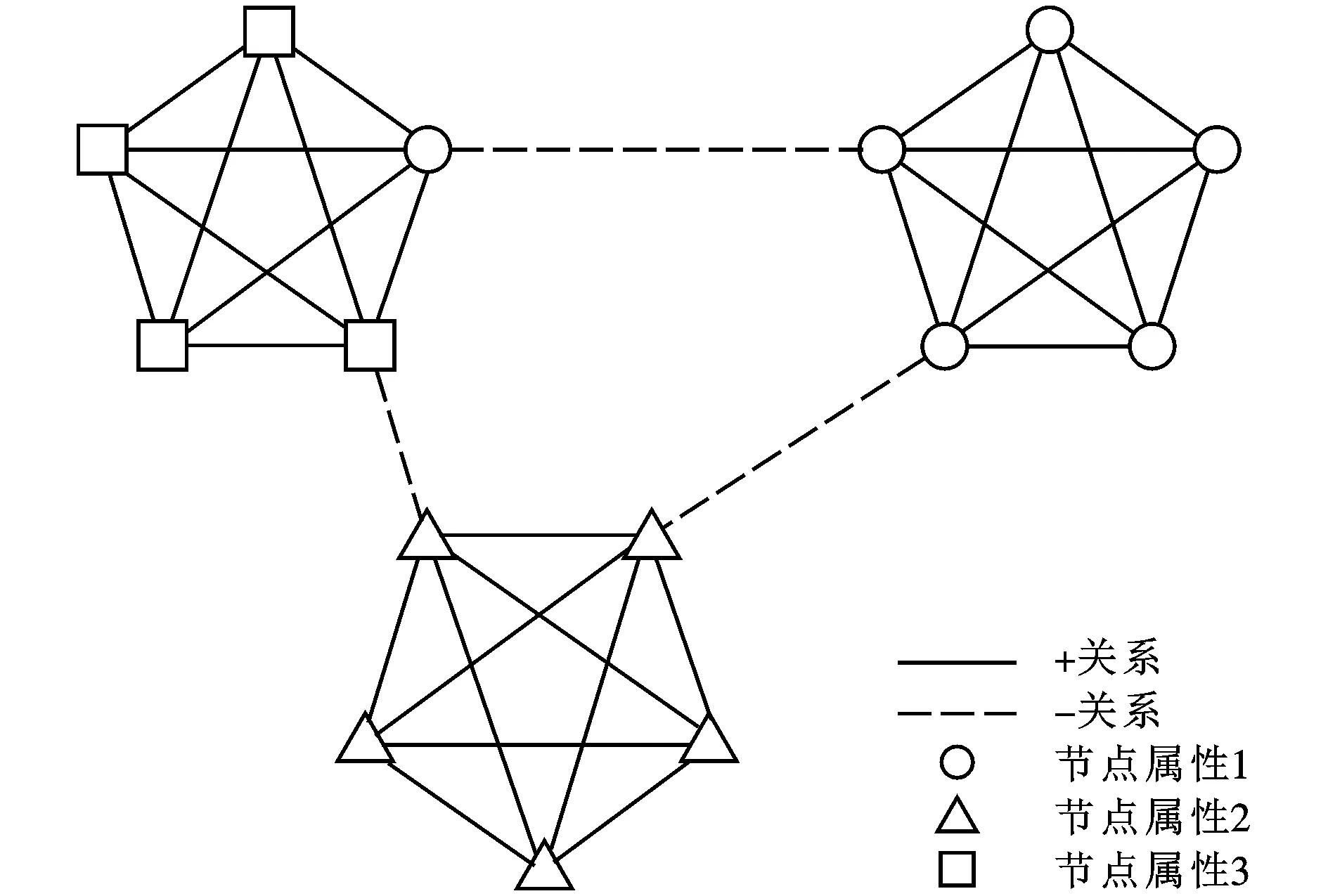
图1 全符号网络的理想社群结构

本文以下部分将构造全符号网络的社群结构指标。首先,Newman通过与随机网络对比,从网络结构属性层面提出了测度0-1网络社群结构特征的模块度QN,该指标表示一个网络社群内部的连接与随机网络连接的期望值比较,QN值越大表明社群内部连接的更紧密,即社群结构特征更为明显[3]。QN的表达式如下

(1)

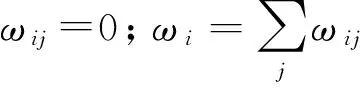
(2)

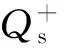
(3)

(4)

放榜前一天我透过电话查询榜单，电话拨通后输入准考证号码，三秒钟后便听见答录机中传来甜美的女声：“蔡修齐同学您好。恭喜您录取国立OO大学XX工程学系。”

基于上述研究,针对考虑了节点属性的全符号网络,本文构建出全符号网络的模块度Qf,表达式如下

(5)

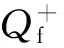
(6)

(7)

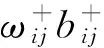
因此,本文提出的全符号网络模块度指标是前两类模块度指标的更广泛的形式,不仅可以有效地将节点、关系与结构共同纳入同一个指标体系当中,也适用于前两类指标所测度的社群结构问题。为进一步说明本文指标的适用性与有效性,本文在图1基础上做一定的调整,给出结构近似的3个网络,如图2所示。如上文所述,图1为理想的全符号网络社群结构,该网络具有社群内部节点属性相同、关系紧密且以正边相连,同时社群之间节点属性不同、关系稀疏且以负边相连的特征;图2a在其基础上将社群内部的一条边转移到社群之间,从而降低社群内部关系的紧密型与社群之间关系的稀疏性,使其结构属性特征减弱;图2b在理想结构的基础上将社群内部的一条正边变为负边,降低其关系属性特征;图2c在图1的基础上调整了一个个体的属性,使得社群内部的节点属性不再统一。表1列出了针对4种不同网络结构的3类指标计算结果,通过与理想结构对比可知,QN可以衡量出社群结构的结构属性特征,但不能反映关系属性与节点属性的变化;Qs可以反映结构属性与关系属性,但不能反映节点属性的变化;Qf则可以全面反映网络结构、边属性和节点属性的变化。

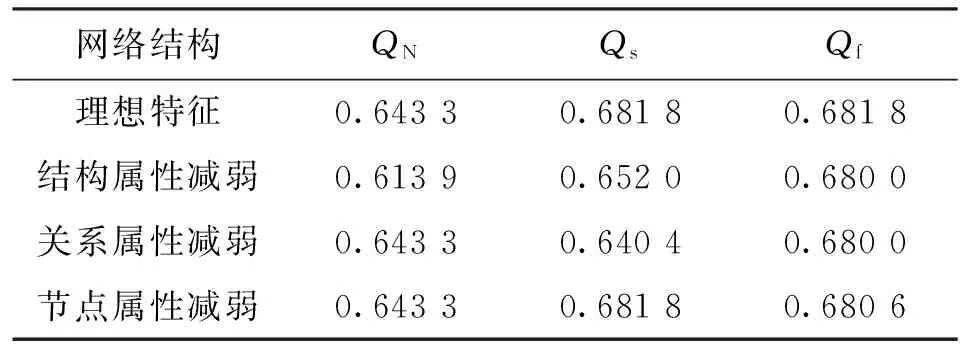
表1 针对不同网络结构的3类指标计算结果

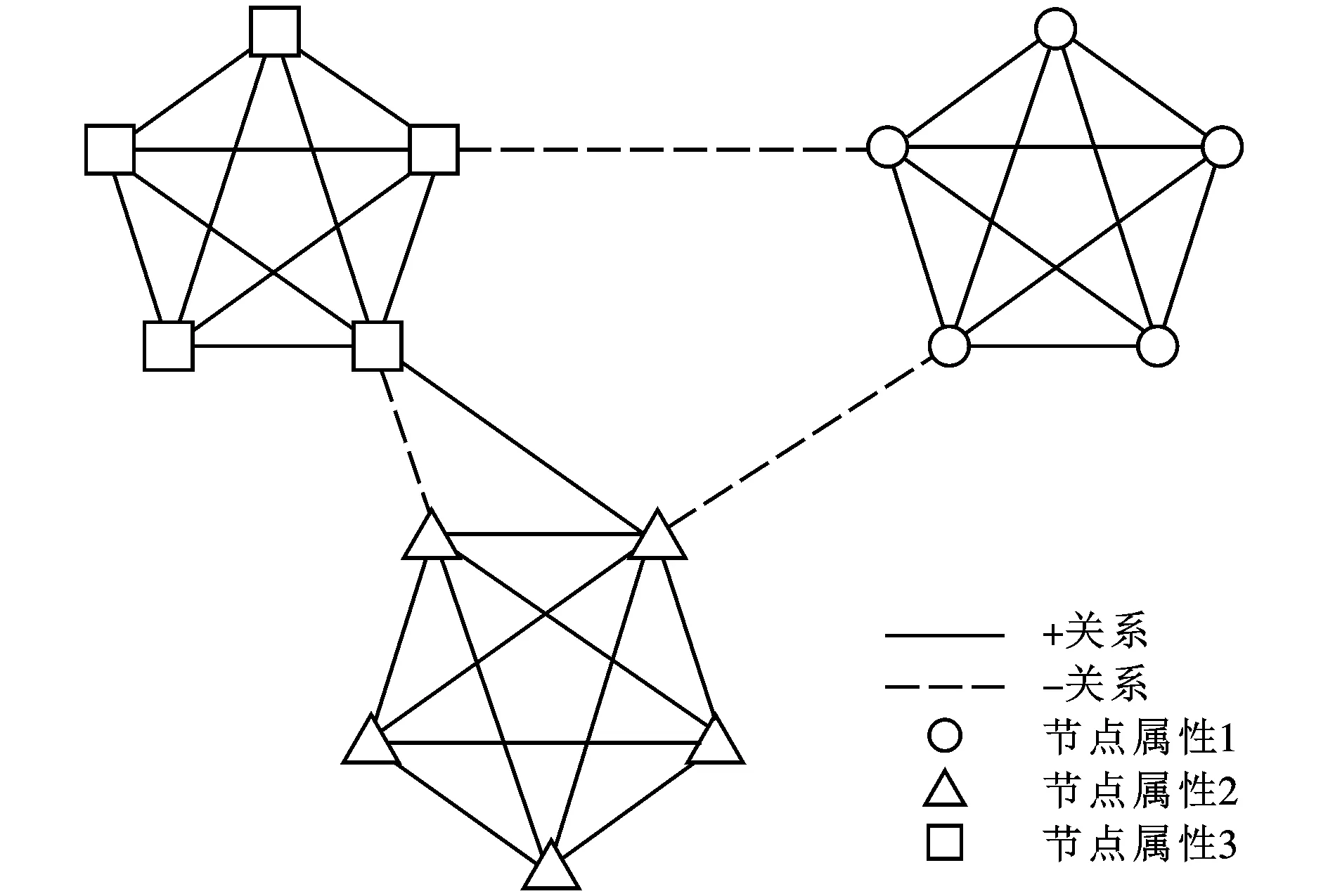
(a)结构属性特征减弱

(b)关系属性特征减弱

(c)个体属性特征减弱图2 社群结构特征对比

2 全符号网络社群结构探测算法

与0-1网络的社群结构探测类似,全符号网络社群结构探测的问题也是一个组合优化问题,其计算复杂度更高,因此传统方法难以有效解决全符号网络社群结构探测问题。社群结构探测算法通常可以归结为以下3类:①自顶向下的算法,即将大社群一步步拆分为较小社群的方法[3,18];②自底向上的算法,即将小社群一步步合并为较大社群的方法[19-22];③以遗传策略或是模拟退火策略为代表的启发式混合算法[23-24]。为了降低复杂度,本文引入复杂度较低的遗传算法,其算法框架参照文献[25],称为算法1。首先输入必要的参数、邻接矩阵以及节点的属性序列,通过初始化函数InitialPopulation(·)生成种群P;然后进入循环,直到迭代次数达到设定的最大迭代次数,在循环中,首先利用选择操作Selection(·)以轮盘赌方式选择父代种群,随后利用遗传操作GeneticOperation(·)对父代种群进行交叉与变异操作,通过更新操作UpdatePopulation(·)更新种群,得到更好的染色体种群;最后输出计算的结果。算法1的框架如下。

2.输入初始邻接矩阵;

3.输入初始节点属性;

4.P←InitialPopulation (Spop);

5.fori=1;i

6.Pparent←Selection(P,Spool,Stour);

7.Pchild←GeneticOperation(Pparent,Pc,Pm);

8.P←UpdatePopulation(P,Pnewchild);

9.end for

10.输出最优种群。

3 实验结果与讨论

为了进一步评估本文所提模块度的适用性以及算法的有效性,本文将在计算机生成网络上进行实验,所有实验在2.40 GHz CPU,4.00 GB内存以及Windows 7系统运行,编程语言为MATLAB。本文的计算机生成网络是对Newman所提出的模拟网络进行改进后的网络[3],原模拟网络结构由128个节点与4个社群构成,节点的平均度值为16,并通过外部社群间的连接概率μ来分配社群外部与社群内部边的连接。由于实验对象为带有节点属性与边属性的全符号网络,因此本文在原模拟网络基础上将每个节点属性按1～4随机赋值,同时引入参数β来表示社群内部连接负边的概率以及社群之间连接正边的概率。

为衡量本文算法所探测到的社群结构与实际社群结构的差异,本文采用标准化互信息(Normalized Mutual Information,NMI)指数INM来作为评价指标[26],INM越大表明二者差异越小,该指数可以有效分析社群结构的探测效果[25,27],其公式如下

(8)

式中:Ca、Cb表示a、b两种探测结果的社群数量;Cij是探测结果a的社群i与探测结果b的社群j的共同节点数量;Ci、Cj是Cij在社群i、j的节点总数;N是节点数量。如果INM(a,b)=1,则说明社群结构的探测结果与实际社群结构相同,如果INM(a,b)=0,则说明社群结构的探测结果与实际社群结构完全不同。

本文分别基于3种模块度指标Qf、Qs与QN对社群进行控测,将μ与β的取值范围设为0～0.5,由9×6组实验数据构成。为减少随机性误差,每个μ与β值对应的网络结构分别依据不同指标进行5次独立实验,其标准化互信息指数INM的平均值如图3所示。

(a)基于全符号网络模块度所得结果

(b)基于经典符号网络模块度所得结果

(c)基于Newman的模块度所得结果图3 不同μ与β值所对应的社群探测结果

从图3可以看出:基于3类指标的探测方法所获得的INM指数均会随μ值的增加而减小,即随着社群外部连接概率的增加,原有网络社群结构开始模糊,3类方法所探测的结果都更接近真实的网络社群结构;对于β值的变化,基于全符号网络与经典符号网络模块度所获得的INM指数会随β值的增加而降低,但基于Newman模块度所获得的INM指数不受β值的影响。β值的增加表示网络社群结构的关系属性特征降低,由于Newman的模块度并不能反映出网络的关系属性,因而其结果不会受β值影响。由此看出,基于全符号网络与经典符号网络模块度的社群探测算法能够同时反映出社群结构的结构属性特征与关系属性特征的变化。

在进一步实验中,为检验节点属性对于社群探测结果的影响,本文引入新的参数γ来表示社群内部节点属性的异众比率。本次实验将μ与β的取值固定,将γ范围设为0～0.5,并分别依据不同指标进行5次独立实验。取μ=0.25、β=0.2时,每个γ对应的INM指数的平均值如图4所示。

图4 不同γ值所对应的社群探测结果

从图4可以看出:基于Newman的模块度与经典符号网络模块度所探测的结果并不受节点属性的影响;基于全符号网络模块度所计算的INM指数随γ的增加而降低,即随着社群内部节点属性调整,社群结构的节点属性特征有所变化;基于全符号网络模块性的探测算法可以有效反映出节点属性对于社群结构探测的影响。

4 结论与展望

本文同时从节点属性层面、关系层面与结构层面探索了全符号网络下的社群结构。以Newman所提出的模块度指标作为基础,将结构平衡理论与同质性准则共同纳入指标体系的构建中,得到全符号网络下的社群结构指标,为社群结构分析提供了全新的视角。为了计算新型的社群结构指标,并探测出网络的社群结构,本文提出了基于遗传算法的数学模型。实验结果表明,本文所提出的算法可以有效地探测出网络的社群结构,同时全符号网络的模块度指标可以同时反映出网络的结构、关系、节点属性特征的变化。然而,本文所提出的社群探测算法为复杂度较低、过程较为简易的遗传算法,有易于陷入局部最优的缺陷,进一步提出更有效的算法,并与相关算法进行比较是本文的后续研究。同时,本团队将进一步利用多目标优化的求解方法,对结构、关系、节点3个层次属性进行优化。此外,由于本文所提出的算法模型只是静态的求解方法,有关动态的网络结构优化还需要进一步探讨。

[1] WATTS D J, STROGATZ S H. Collective dynamics of ‘small-world’ networks [J]. Nature, 1998, 393(6684): 440-442.

[3] GIRVAN M, NEWMAN M E J. Community structure in social and biological networks [J]. Proceedings of the National Academy of Sciences of the United States of America, 2002, 99(12): 7821-7826.

[4] DOREIAN P, MRVAR A. Partitioning signed social networks [J]. Social Networks, 2009, 31(1): 1-11.

[5] HEIDER F. Social perception and phenomenal causality [J]. Psychological Review, 1944, 51(6): 358-374.

[6] HEIDER F. Attitudes and cognitive organization [J]. Journal of Psychology, 1946, 21(1): 107-112.

[7] CARTWRIGHT D, HARARY F. Structural balance: a generalization of Heider’s theory [J]. Psychological Review, 1956, 63(5): 277-292.

[8] 李振鹏, 唐锡晋. 社会影响、观点动向和结构平衡: 基于Hopfield网络模型仿真研究 [J]. 系统工程理论与实践, 2013, 33(2): 420-429. LI Zhenpeng, TANG Xijin. Social influence, opinion dynamics and structure balance: a simulation study based on Hopfield network model [J]. Systems Engineering: Theory and Practice, 2013, 33(2): 420-429.

[10]ROGERS E M, BHOWMIK D K. Homophily-heterophily: relational concepts for communication research [J]. Public Opinion Quarterly, 1970, 34: 523-538.

[11]KANDEL D B. Homophily, selection, and socialization in adolescent friendships [J]. American Journal of Sociology, 1978, 84: 427-436.

[12]KOSSINETS G, WATTS D J. Origins of homophily in an evolving social network [J]. American Journal of Sociology, 2009, 115: 405-450.

[13]MCPHERSON M, SMITH-LOVIN L, COOK J M. Birds of a feather Homophily in social networks [J]. Annual Review of Sociology, 2001, 27(1): 415-444.

[14]张锴琦, 杜海峰, 蔡萌, 等. 基于节点属性的社群结构探测算法改进 [J]. 系统工程理论与实践, 2013, 33(11): 2879-2886. ZHANG Kaiqi, DU Haifeng, CAI Meng, et al. Improved community structure detection algorithm based on the node’s property [J]. Systems Engineering: Theory and Practice, 2013, 33(11): 2879-2886.

[15]DU H, HE X, FELDMAN M W. Structural balance in fully signed networks [J]. Complexity, 2016, 21(S1): 497-511.

[16]李树茁, 任义科, 费尔德曼, 等. 中国农民工的整体社会网络特征分析 [J]. 中国人口科学, 2006(3): 19-29. LI Shuzhuo, REN Yike, FELDMAN M W, et al. Analysis of whole social network properties of rural-urban migrants in China [J]. Chinese Journal of Population Science, 2006(3): 19-29.

[17]任义科, 杜海峰, 李树茁. 农民工社会网络的核心边缘结构分析 [J]. 人口与发展, 2010, 16(6): 2-16. REN Yike, DU Haifeng, LI Shuzhuo. Analysis of core-periphery structure of Chinese rural-urban migrants’ social network [J]. Population and Development, 2010, 16(6): 2-16.

[18]WHITE S, SMYTH P. A spectral clustering approach to finding communities in graph [C]∥SIAM International Conference on Data Mining. Philadelphia, PA, USA: SIAM, 2005: 274-285.

[19]NEWMAN M E J. Fast algorithm for detecting community structure in networks [J]. Physical Review: E Statistical Nonlinear & Soft Matter Physics, 2004, 69(6): 066133.

[20]CLAUSET A, NEWMAN M E, MOORE C. Finding community structure in very large networks [J]. Physical Review: E, 2005, 70(6): 264-277.

[21]WANG X, CHEN G, LU H. A very fast algorithm for detecting community structures in complex networks [J]. Physica: A Statistical Mechanics & Its Applications, 2007, 384(2): 667-674.

[22]BLONDEL V D, GUILLAUME J L, LAMBIOTTE R, et al. Fast unfolding of communities in large networks [J]. Journal of Statistical Mechanics Theory & Experiment, 2008, 2008(10): 155-168.

[24]LI S, CHEN Y, DU H, et al. A genetic algorithm with local search strategy for improved detection of community structure [J]. Complexity, 2010, 15(4): 53-60.

[25]GONG M, FU B, JIAO L, et al. Memetic algorithm for community detection in networks [J]. Physical Review: E, 2011, 84(5): 056101.

[26]DANON L, DIAZ-GUILERA A, DUCH J, et al. Comparing community structure identification [J]. Journal of Statistical Mechanics: Theory and Experiment, 2005(9): P09008.

[27]GONG M, CAI Q, CHEN X, et al. Complex network clustering by multiobjective discrete particle swarm optimization based on decomposition [J]. IEEE Transactions on Evolutionary Computation, 2014, 18(1): 82-97.

[本刊相关文献链接]

周亚东,刘丽丽,张贝贝,等.在线社会网络中多话题竞态传播分析与建模.2017,51(2):1-5.[doi:10.7652/xjtuxb2017 02001]

杨沫,由磊,李冰,等.采用传递概率与社会网络分析的延迟容忍网络路由.2016,50(12):136-141.[doi:10.7652/xjtuxb 201612021]

李刘强,桂小林,安健,等.采用模糊层次聚类的社会网络重叠社区检测算法.2015,49(2):6-13.[doi:10.7652/xjtuxb 201502002]

杜巍,蔡萌,杜海峰.网络结构鲁棒性指标及应用研究.2010,44(4):93-97.[doi:10.7652/xjtuxb201004020]

李小虎,杜海峰,张进华,等.多层前向小世界神经网络的逼近与容错性能.2010,44(7):59-63.[doi:10.7652/xjtuxb 201007014]