基于ABAQUS的凿岩机钻头破岩数值模拟分析

张 强, 索江伟, 王海舰, 孙国庆, 孙赫威

(1.辽宁工程技术大学 机械工程学院，辽宁 阜新 123000； 2.大连理工大学 工业装备结构分析国家重点实验室，辽宁 大连 116023； 3.四川理工学院 材料腐蚀与防护四川省重点实验室，四川 自贡 643000)

在对隧道开挖和岩体巷道掘进的工程项目中，岩层钻孔作业的需求量很大，而钻孔速度以及钻孔效率高低，对整个工程影响非常大。液压凿岩机作为钻孔破岩的主要工作设备，因其能量利用率高，破岩速度快等优点，在钻孔作业中的应用越来越广泛[1]。伴随着钻孔破岩工程量需求的不断加大，对于钻机在更大钻孔深度、更高岩体硬度和深埋岩层的破岩要求也越来越高。近年来，针对钻孔破岩研究，李俊伟等[2]研究了液压凿岩机钻头与岩体的单次旋转冲击破岩有限元仿真模拟，分析了不同初始冲击能和不同回转速度下钻进深度和凿岩反力的影响。李玮等[3]基于振动学理论，在考虑岩石重力的情况下，建立钻头冲击载荷下岩石振动响应的数学模型，分析各参数对钻头高频冲击下岩石振动的影响,并进行了室内实验对理论分析结果进行了验证。董学成等[4]对震荡冲击器作用下井底破岩的数值模拟，分析了不同工作频率、不同循环动载和不同岩体类型下的破岩机理。何霞等[5]建立空气锤钻头与岩石的破岩仿真模型，对钻头破岩过程进行了仿真分析，得到了空气锤钻头的破岩机理。卜长根等[6]对潜孔锤瞬态冲击凿岩过程进行数值模拟，研究了球齿钻头在凿入不同空隙率岩石中的冲击力特性。黄志强等[7]建立钻头与岩石的仿真模型，将钻头定义为线弹性模型，岩石定义为塑性应变失效模型，对钻头在单次冲击下的岩石破碎机理进行了动力学仿真研究。祝效华等[8]以Drucker-Prager准则作为岩石的本构关系，建立了PDC切削齿动态破岩的三维仿真模型，分析了后倾角侧倾角切削深度围压等因素对破岩能效的影响。祝效华等[9]利用LS-DYNA建立空气冲旋钻井活塞-钻头-岩石相互作用系统模型，研究PGP-X井钻井参量及空气锤结构参量与冲击功及破岩比功的关系，对冲击末速度、钻压、冲击频率、转速、井深等破岩能效的影响进行了分析。舒敏飞等[10]提出了基于液压油液受压缩建立液压凿岩机工作压力的理论，建立Amesim仿真平台进行了仿真和分析，验证了理论的合理性，并揭示了冲击性能、工作压力与输入流量、活塞质量、活塞油压作用面积、蓄能器充气压力之间的关系。Bu等[11]则是通过ANSYS 软件里的LS-DYNA模块对潜孔锤、钻头、岩石这几者之间相互作用的瞬态冲击动力学有关问题进行了研究。

目前针对液压凿岩机破岩方面的研究还存在需要完善之处：首先，对液压凿岩机钻头在回转-冲击载荷下的岩体连续破碎过程的数值模拟分析还有待进一步研究；其次，没有考虑不同初始地应力情况下对液压凿岩机破岩的影响。为进一步改善液压凿岩机破岩效果和工作性能，笔者利用大型有限元分析软件ABAQUS对液压凿岩机钻头的连续破岩过程进行了数值模拟，研究不同工况对破岩效果的影响。

1 建立数值模型

1.1 模型假设

液压凿岩机主要是依靠冲击活塞撞击钎尾，将冲击能以应力波的形式通过钎杆传递给钎头，由钎头冲击凿岩，活塞回程时带动钎子回转一定角度，如此反复的冲击回转作用将岩体破碎，破碎的岩粉由排粉机构不断从孔底排出孔外。为了更好的分析钻头破岩过程，在不影响岩体受力情况下对模型作如下假设：

① 将钎头、连接套和钎杆当作是一个整体的刚体来看待，只考虑钻头冲击凿岩过程中钻进系统在沿着轴向方向上的整体受力状况[12]，在整个破岩过程中不考虑其变形和磨损；② 将冲击活塞撞击钎尾的冲击能简化为一个等效冲击力直接作用于模型末端；③ 对岩体视为连续的、均匀的、各向同性的介质]，不考虑岩体中的原生裂纹及岩体内部孔隙压力影响；④ 假设破碎后的岩屑能够迅速离开钻孔，即破碎失效的岩体单元即刻被删除。

1.2 网格划分

通过Pro/Engineer建立钻头直径为89 mm的简化后钎头、连接套和钎杆整体物理模型，再导入有限元分析软件中；在ABAQUS中直接建立尺寸为350 mm×350 mm×200 mm的岩体模型。对钻头整体部分采用10节点四面体单元(C3D10M)自由网格划分，网格节点总数为9 290；岩体部分采用8节点缩减积分单元(C3D8R)扫掠网格划分技术，中轴算法，将岩体划分成中心密集周围疏松的网格单元，这样既节省计算时间又保证计算精度，节点总数为377 076。网格划分情况,如图1所示。

图1 钻头和岩体的网格划分模型

1.3 材料参数设置

岩体本构模型采用Drucker-Prager模型，即线弹性模型和扩展Drucker-Prager破坏准则联合使用的一种理想弹塑性模型，这种模型被广泛应用于岩土力学数值计算分析中[13-14]。在这里认为冲击部分的质量惯量全部集中于简化后的钻头模型上，所以钻头模型密度在这里采用等效密度。材料基本参数设置,如表1所示[15]。

表1 模型所用材料基本参数

1.4 边界条件、载荷、接触及分析步设置

岩体的边界条件，将初始地应力设置为：垂直应力设为10 MPa，地应力侧压系数设为1，除与钻头接触的岩石边界外，其余五个边界面定义为无限无反射边界条件以模拟无限区域的情况[16]。笔者以COP1838ME/HE型号掘进凿岩台车用液压凿岩机性能参数为主要依据来设定对冲击钻头的载荷和边界条件。固定钻头在X，Y方向的位移和转动约束，保证钻头在钻进过程中只进行沿Z轴移动及绕Z轴转动；通常轴推力大小为15～20 kN，在这里选取20 kN，回转速度设为300 r/min，冲击频率设为60 Hz。

通常情况下，液压凿岩机冲击机构的活塞冲击停顿时间为：0.5～0.6 ms[17]，在这里认为活塞撞击钎尾后速度变为零，根据动能定理和动量定理可得等效冲击力。

(1)

式中:E为冲击能，J；m为活塞重量，kg，这里取10 kg，v为活塞冲击末速度，m/s；t为活塞冲击钎尾停顿时间，ms，在这里取0.5 ms；F为等效冲击力，kN。

设置冲击能为300 J，将冲击能等效成一个瞬时冲击力载荷施加于钻头上，由式(1)计算可得冲击力大小为155 kN。边界情况和载荷模型,如图2所示。

模型中，钻头与岩体间接触采用ABAQUS explicit中面-面接触类型，钻头表面为主面，岩体表面为从面，采用有限滑动公式，法向属性选用硬接触。定义两个分析步，第一个分析步对钻头施加200 N的轴向推力，使钻头与岩体表面平稳接触，第二个分析步施加上所有载荷，分析时间控制为0.5 s。

2 数值仿真结果分析

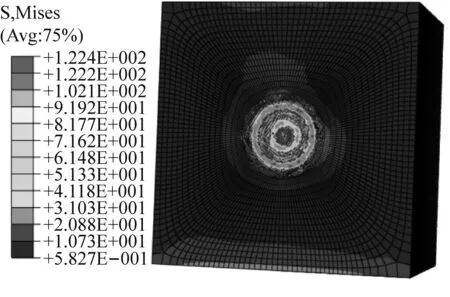
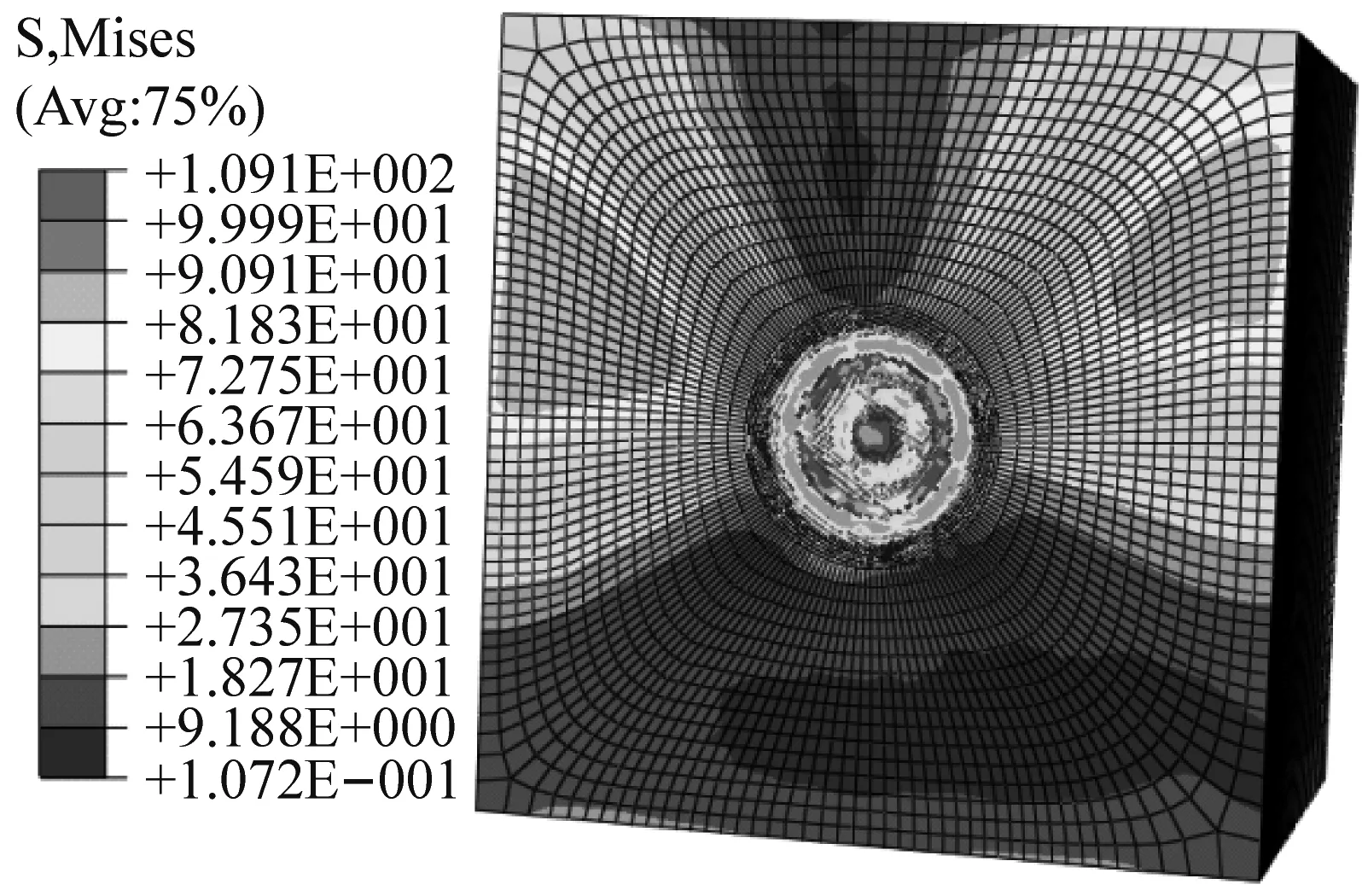
图3为分析破岩仿真结果的应力云图，由图3可知，钻头在回转-冲击载荷作用下确实对岩体造成了破碎，且形成了比较规则的破碎孔。

钻头破岩过程速度和深度变化曲线如图4所示。由图4可知，在开始破碎阶段，钻头的第一排齿最先跟岩体接触，且在外载荷作用下逐渐侵入岩体内部，在作用到0.15 s左右时，整个钻头部分与岩体发生撞击，钻头速度急剧下降，但在轴推力作用下，钻头与岩体接触部分基本没有发生分离，之后钻头速度逐渐增大继续破岩。

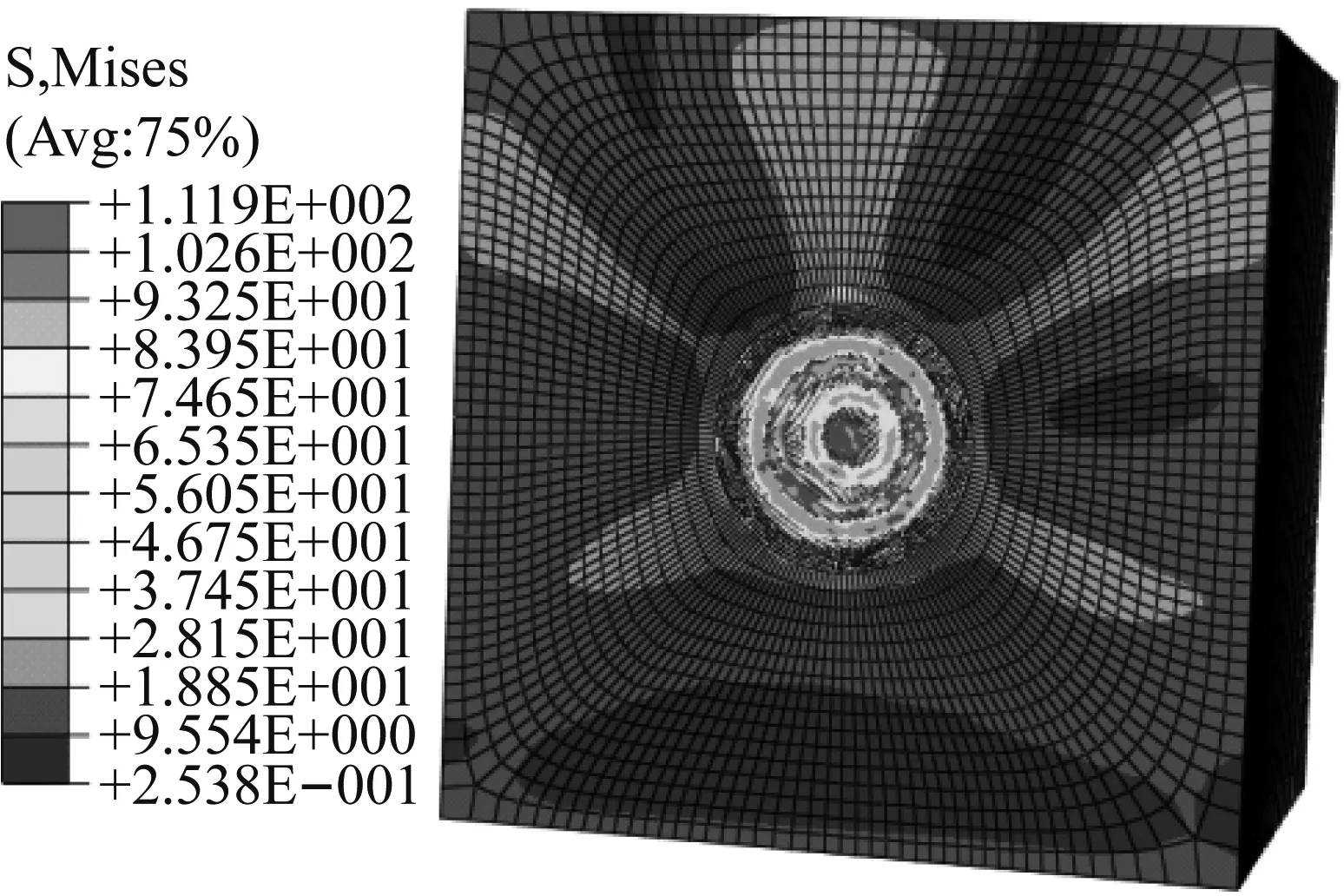
图3 破岩仿真结果应力云图

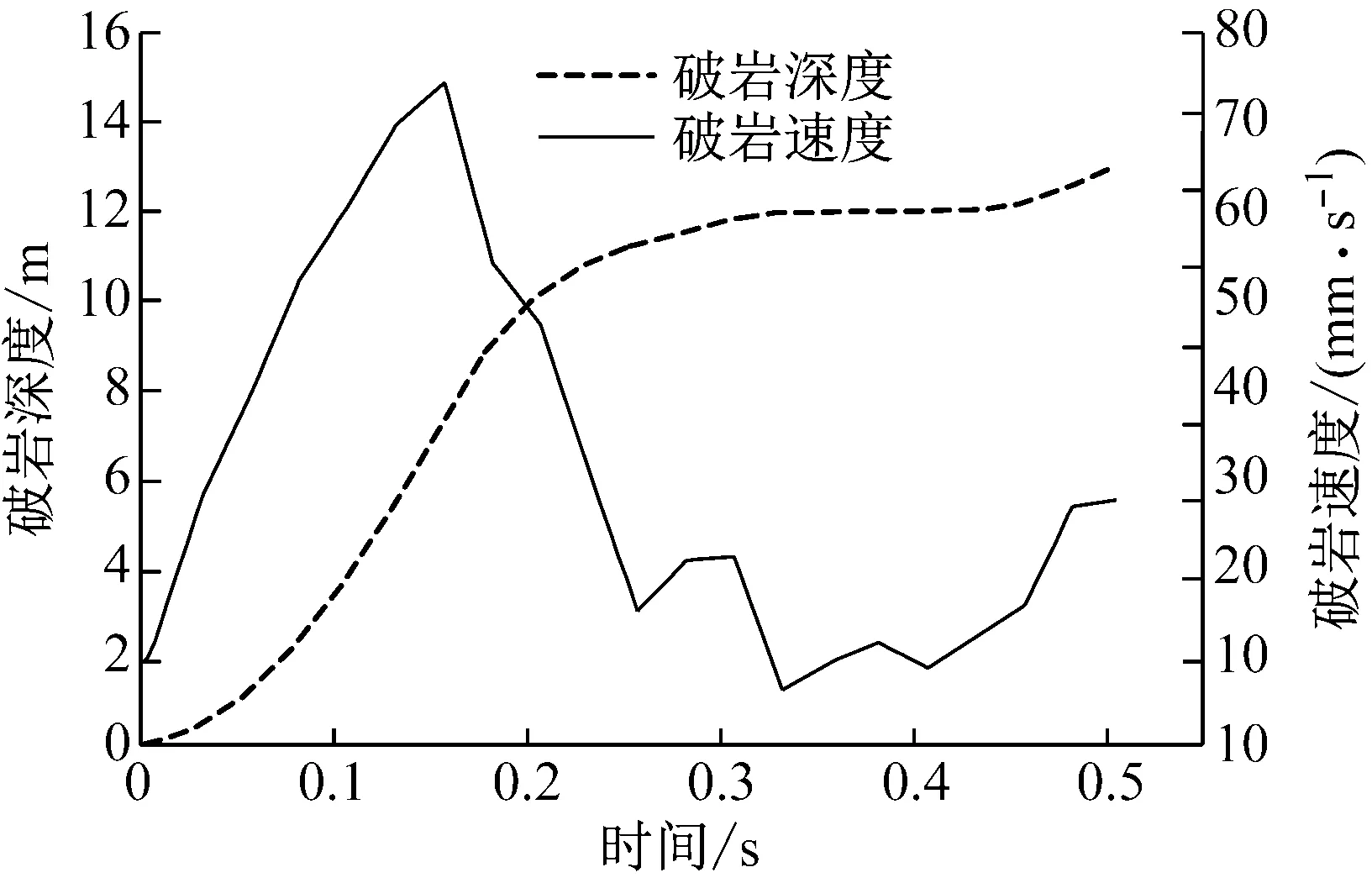
图4 破岩过程速度和深度变化曲线

图5为破岩过程能量消耗变化曲线。根据图5可知，随着破碎时间的积累，能量消耗也在不断升高。整个破岩过程基本吻合实际中液压凿岩机钻孔过程，且数值模拟的钻进速度也符合实际钻进速度范围，所以笔者认为运用ABAQUS软件对凿岩机钻头破岩过程的数值模拟结果可以为实际工程中提供必要的理论参考。

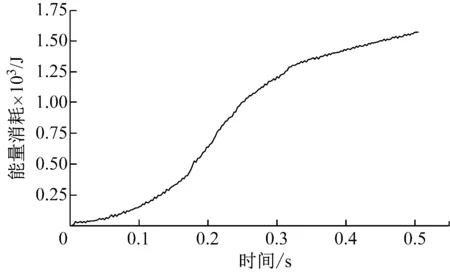
图5 破岩过程能量消耗变化曲线

3 不同工况下破岩过程的影响分析

在液压凿岩机实际作业中，冲击频率和回转速度是影响破岩效果的重要性能参数，选取合适的性能参数对整个破岩过程至关重要。破岩速度是表示破岩快慢的物理量；破岩比能是指破碎单位体积岩石所消耗的能量，是破碎效率高低的重要标志。在ABAQUS explicit分析模块中可以直接提取整个分析过程中外载荷做功的能量变化曲线，而破碎体积即模拟过程中失效的单元部分。

对不同工况下，模拟结果进行比较：取冲击频率为60 Hz，回转速度为200 r/min、250 r/min和300 r/min三组破碎坑应力云图，在破碎坑边界的上、下、左、右四个方向分别选取1 784、2 269、876、3 000四个网格节点，通过节点在破碎坑边界分布情况，如图6所示，可知每组破碎坑的横截面积几乎保持不变，所以在此认为，模拟破碎过程中，钻头侵入相同深度岩体时对岩体的破碎体积基本一致，又因为岩体的破碎体积不便于计算，在这里以破碎单位深度所消耗的能量代替破岩比能，用单位深度消耗能量和破岩速度综合分析对破岩效果的影响。

(a) 200 r/min

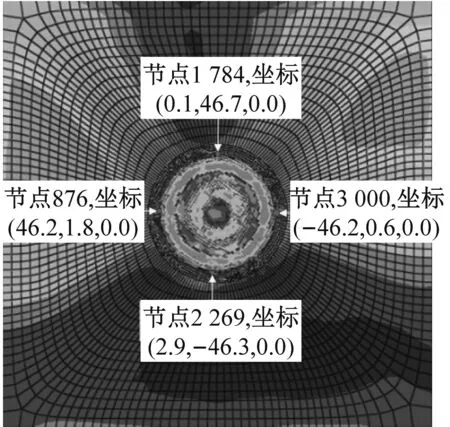
(b) 250 r/min

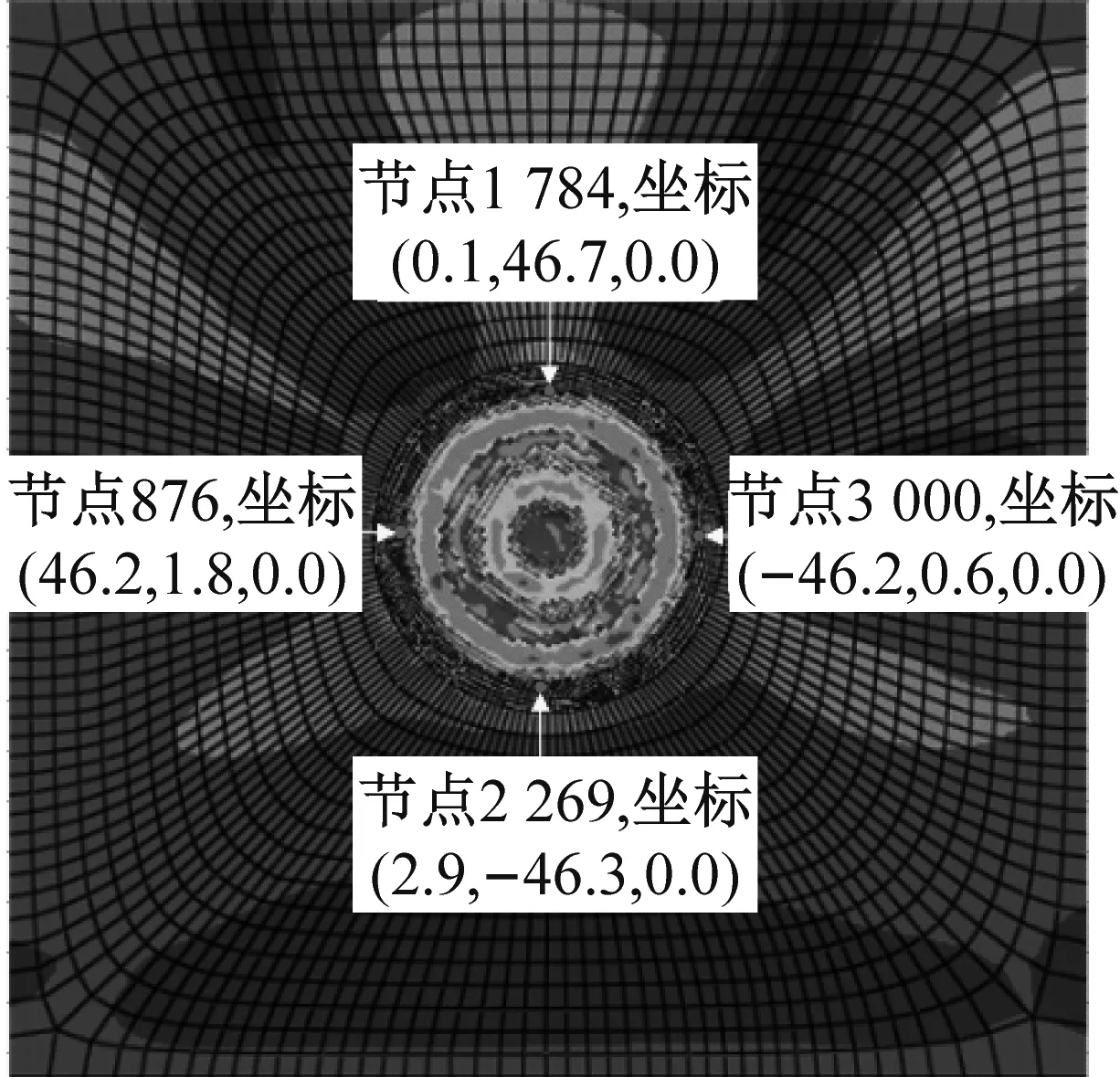
(c) 300 r/min

3.1 回转速度对破岩的影响

在工程实际中，液压凿岩机回转速度大小基本上在200～400 r/min的范围内变化。所以，为分析回转速度对破岩过程的影响，在保证其它参数不变条件下，分别又对200 r/min、250 r/min、350 r/min、400 r/min四种回转速度工况进行模拟分析，将结果数据经过MATLAB拟合后，得到单位深度消耗能量-回转速度-破岩速度关系曲线和不同回转速度下破岩模拟结果的应力云图，分别如图7和图8所示。

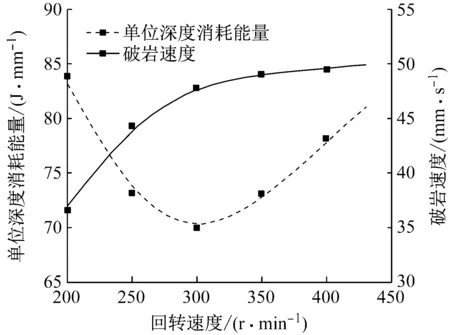
图7 单位深度消耗能量-回转速度-破岩速度关系曲线

Fig.7 The energy consumption of per unit depth-rotary speed-rock breaking speed curve

通过分析不同回转速度情况下对破岩速度的影响，可以得到，随着回转速度增大破岩速度也随之增大，但变化幅度逐渐减小，当速度达到300 r/min以后，破岩速度几乎不再改变；所以，笔者认为在液压凿岩机破岩过程中，在一定范围内回转速度的改变对破岩速度有明显影响，但当回转速度达到某一值之后，再增加回转速度对破岩速度的影响可以忽略。从能耗的角度分析，可知速度在 200～250 r/min阶段，随回转速度增大能耗快速降低；250～300 r/min阶段能耗缓慢降低，当速度超过300 r/min时，能耗开始升高；所以，可以知道破岩效率随着回转速度的增加表现为先升高后降低的变化趋势。综合考虑破岩速度和破岩效率对破岩效果的影响，笔者认为在针对本文所设定岩石参数的情况下，回转速度在300 r/min左右时，具有高破岩速度和低能耗的特点，此时破岩效果最好。

3.2 冲击频率对破岩的影响

在实际作业中，液压凿岩机工作的冲击频率基本上在30～100 Hz的范围内设定。为了分析冲击频率对破岩过程的影响，在保证其它参数不变的条件下，对40 Hz、50 Hz、70 Hz、80 Hz四种冲击频率情况进行模拟分析，将结果数据经过MATLAB拟合后，得到单位深度消耗能量-冲击频率-破岩速度关系曲线，如图9所示。

通过分析关系曲线，可知随着冲击频率增加破岩速度明显增大；在40～60 Hz的范围内，随着冲击频率的增加，单位深度消耗能量快速降低，60～70 Hz阶段能耗缓慢降低，70～80 Hz阶段能耗开始升高；所以，笔者认为冲击频率为70 Hz左右时，破岩效果最好。

(a) 200 r/min

(b) 250 r/min

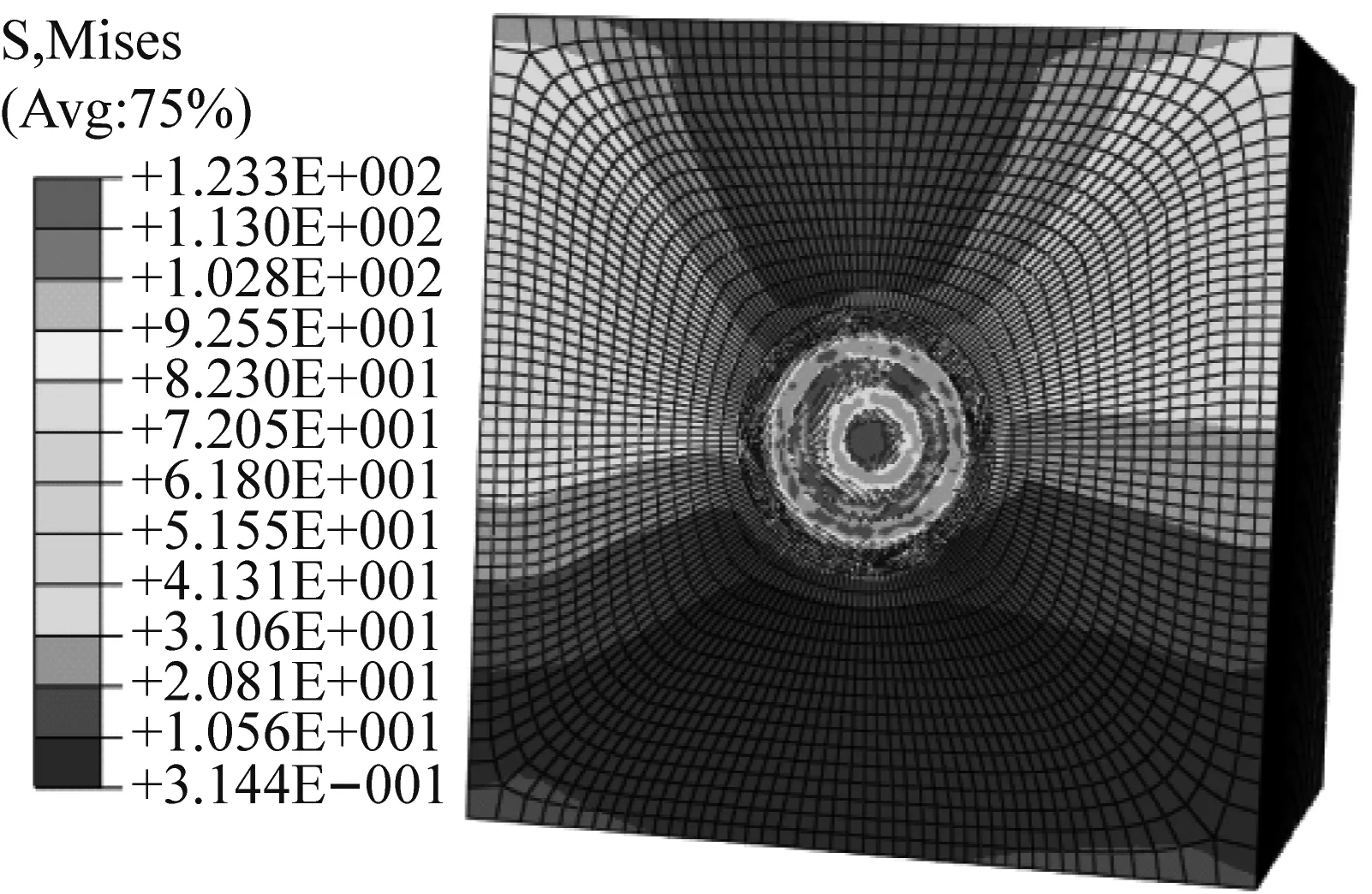
(c) 350 r/min

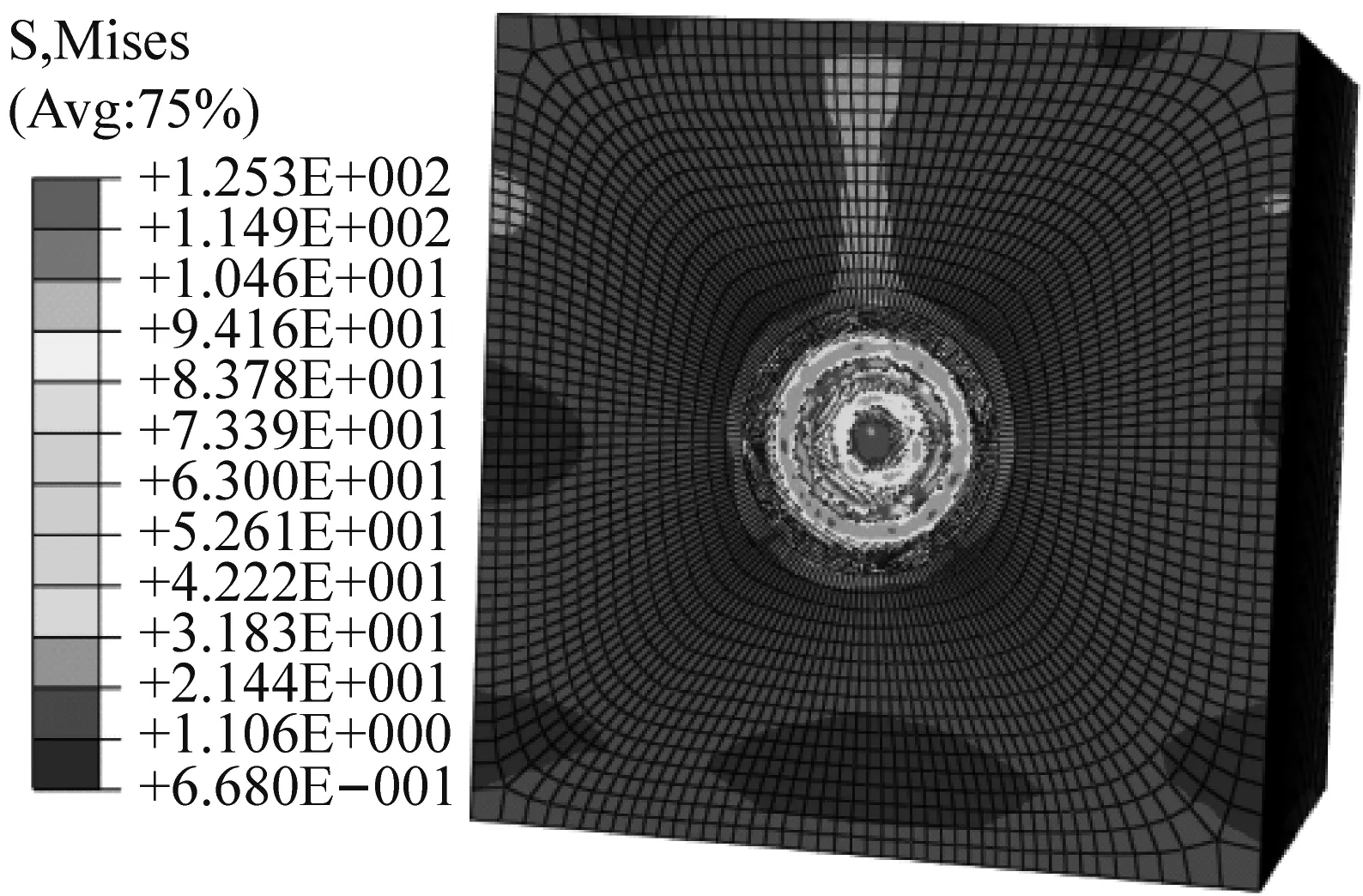
(d) 400 r/min

图9 单位深度消耗能量-冲击频率-破岩速度关系曲线

Fig.9 The energy consumption of per unit depth-impact frequency-rock breaking speed curve

3.3 初始地应力对破岩的影响

为了分析岩石在不同初始地应力[18]情况下对破岩的影响，在不改变其他参数条件下，对无初始地应力和垂直应力分别为22 MPa、34 MPa、46 MPa四种工况下破岩情况进行数值模拟，将结果数据经过MATLAB拟合后，得到单位深度消耗能量-初始地应力-破岩速度关系曲线，如图10所示。

分析不同的初始地应力下对破岩的影响，可知初始地应力较小时破岩速度变化很小，随着地应力的增大，破岩速度缓慢降低。从能耗角度分析可知，初始地应力在0～10 MPa的范围内时，破岩能耗几乎不变，而当初始地应力增大到10 MPa后破岩能耗迅速增加。

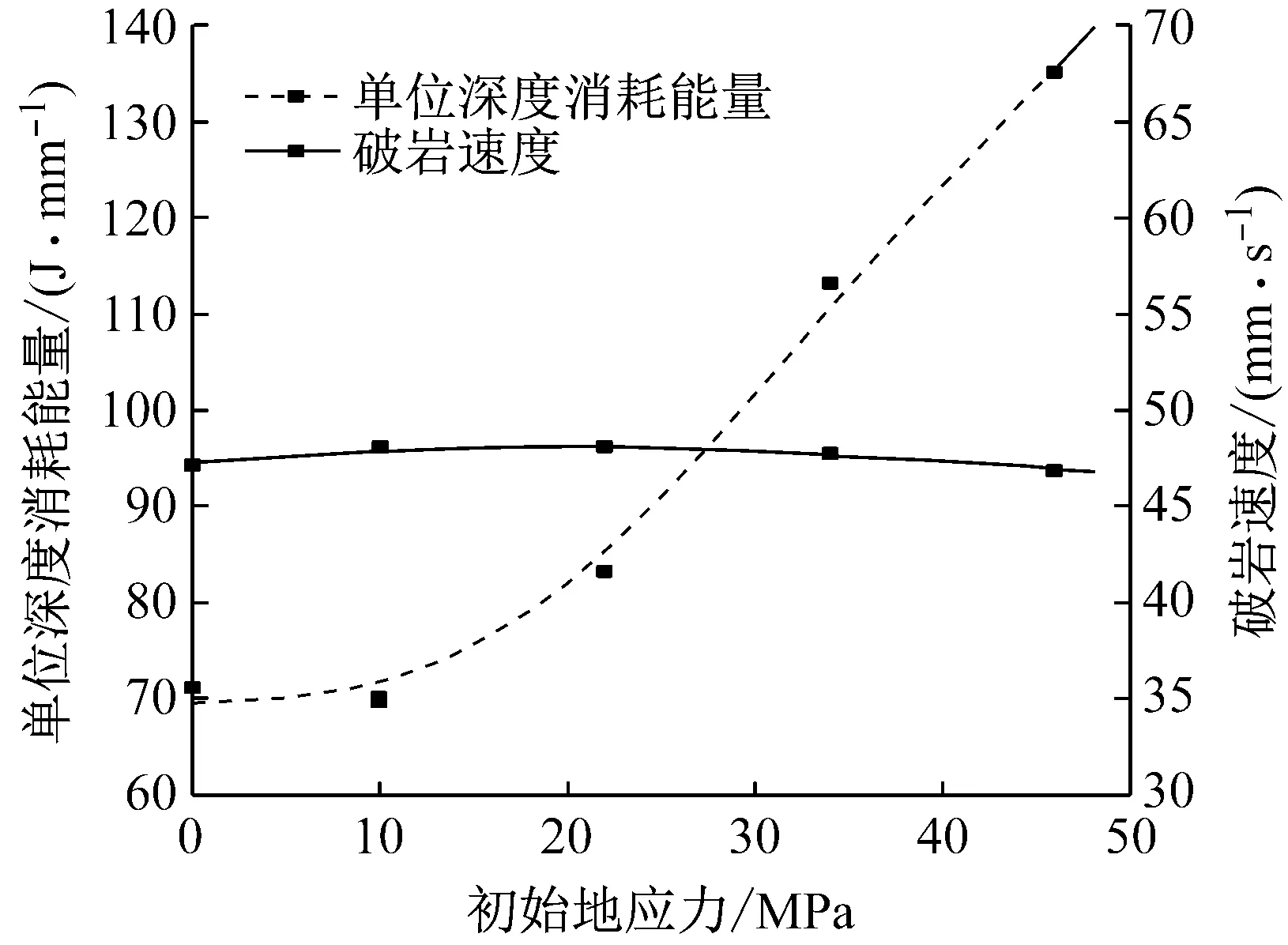
图10 单位深度消耗能量-初始地应力-破岩速度关系曲线

Fig.10 The energy consumption of per unit depth-initial crustal stress-rock breaking speed curve

分析原因可知，因为岩石在高地应力情况下发生一定应变强化特性，对岩石破碎带来更大的难度。

所以，这就要求在实际破岩过程中，当初始地应力较小时，可以保持液压凿岩机最优的工作参数不变，但当破碎深埋岩层地应力较大时，应该相应的改变工作参数，以便具有最好的破岩效果。

4 结 论

本文以花岗岩为研究对象，属于硬质岩石，岩石硬度系数：f=11～15(普氏硬度系数)，对不同回转速度和冲击频率的研究是以岩石受10 MPa围压条件下进行的，根据本文所研究的岩石工况条件可得到以下结论：

(1) 液压凿岩机的回转速度在250～300 r/min范围内变化时对破岩速度具有明显影响，但当达到300 r/min后，回转速度对破岩速度的影响基本可以忽略，且针对花岗岩的破岩过程，回转速度在300 r/min左右时，同时具有破岩速度快和破岩能耗低的特点，破岩效果最好。

(2) 破岩速度随着冲击频率的增加而不断增加，综合考虑对破岩能耗的影响，当冲击频率为70 Hz时，破岩效果最好。

(3) 初始地应力在0～10 MPa的范围内时，对破岩过程影响很小，在大于10 MPa后，随着初始地应力的改变，对破岩速度影响很小，但对破岩效率有很大影响。

[1] 孙延宗,孙继业.岩巷工程施工掘进工程[M].北京：冶金工业出版社,2011.

[2] 李俊伟,康敬东,李金鹏.凿岩台车钻头破岩有限元仿真分析[J].产品·技术,2015(11):75-77.

LI Junwei,KANG Jingdong,LI Jinpeng.Finite element simulation analysis for the drill bit of the jumbo to break the rock[J]. Technology & Management,2015(11):75-77.

[3] 李玮，纪照生，董智煜，等.基于重整化方法的冲击载荷下岩石振动分析[J].振动与冲击,2016,35 (16):49-54.

LI Wei,JI Zhaosheng,DONG Zhiyu,et al.Vibration analysis of rock under impact loads based on the renormalization method[J].Journal of Vibration and Shock,2016,35(16):49-54.

[4] 董学成, 熊继有，王国华，等.震荡冲击器破岩机理数值模拟分析[J].西南石油大学学报(自然科学版),2014，36(6):160-166.

DONG Xuecheng,XIONG Jiyou, WANG Guohua,et al.Numerical simulation analysis of rock breaking mechanism for oscillation impacter[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2014,36(6):160-166.

[5] 何霞，王德贵，刘清友，等.空气锤钻头破岩机理仿真分析[J].石油机械，2001(7):15-19.

HE Xia,WANG Degui,LIU Qingyou,et al.Air hammer bit breaking rock mechanism simulation analysis[J]. China Petroleum Machinery, 2001(7):15-19.

[6] 卜长根，龚汉松，夏柏如. 空隙率对潜孔锤凿岩瞬态冲击过程的影响[J]. 探矿工程(岩土钻掘工程)，2011，38(4):6-9.

BU Changgen,GONG Hansong,XIA Boru.Simulation study of rock voids rate affecting on impact force of DTH hamme[J]. Exploration Engineering(Rock & Soil Drilling and Tunneling),2011,38(4):6-9.

[7] 黄志强，范永涛，魏振强，等.冲旋钻头破岩机理仿真研究[J].西南石油大学学报(自然科学版),2010,32(1):148-150.

HUANG Zhiqiang,FAN Yongtao，WEI Zhenqiang,et al.Simulation study on rock breaking mechanism of the percussion rotary drill[J].Journal of Southwest Petroleum University(Science & Technology Edition), 2011, 32(1): 148-150.

[8] 祝效华，李海.PDC切削齿破岩效率数值模拟研究[J]. 应用基础与工程科学学报,2015,23(1):182-191.

ZHU Xiaohua,LI Hai.Numerical simulation on mechanical special energy of PDC cutter rock-cutting[J]. Journal of Basic Science and Engineering, 2015,23(1):182-191.

[9] 祝效华，罗衡，贾彦杰.考虑岩体疲劳损伤的空气冲旋钻井破岩数值模拟研究[J].岩石力学与工程学报, 2012,31(4):754-761.

ZHU Xiaohua,LUO Heng,JIA Yanjie.Numerical analysis of air hammer bit drilling based on rock fatigue model[J]. Chinese Journal of Rock Mechanics and Engineering, 2012,31(4): 754-761.

[10] 舒敏飞，何清华，赵宏强，等. 液压凿岩机冲击压力及冲击性能仿真研究[J].武汉理工大学学报，2011,33(8):133-137.

SHU Minfei,HE Qinghua,ZHAO Hongqiang, et al.Study on simulation of impact performance and working pressure of hydraulic drifter [J]. Journal of Wuhan University of Technology, 2011, 33(8):133-137.

[11] BU C G, QU Y G, CHENG Z Q, et al. Numerical simulation of impact on pneumatic DTH hammer percussivedrilling[J]. Journal of Earth Science, 2009,20(5):868-878.

[12] 李侯清. 重型液压凿岩机冲击机构及其液压驱动系统研究[D]. 长沙:中南大学, 2010.

[13] 肖诗云，林皋，王哲.Drucker-Prager材料一致率型本构模型[J].工程力学，2003,20(4):147-151.

XIAO Shiyun,LIN Gao,WANG Zhe. A Drucker-Prager consistent rate-dependent model[J]. Engineering Mechanics,2003,20(4): 147-151.

[14] 刘金龙，栾茂田，许成顺，等.Drucker-Prager准则参数特性分析[J].岩石力学与工程学报，2006,25(增刊2):4010-4015.

LIU Jinlong,LUAN Maotian,XU Chengshun, et al.Study on parametric characters of Drucker-Prager[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(Sup2):4010-4015.

[15] 刘泉声，胡云华，刘滨.基于试验的花岗岩渐进破坏本构模型研究[J].岩土力学，2009,30(2):289-296.

LIU Quansheng,HU Yunhua,LIU Bin.Progressive damage constitutive models of granite based on experimental results [J]. Rock and Soil Mechanics,2009,30(2):289-296.

[16] HARTWAN H L.The simulation of percussion dilling in The laboratory by indexed-blow studies[C].SPE500-PA, 1963.

[17] 田文元.轻型独立回转液压凿压机的研究[D]. 沈阳:东北大学，2005.

[18] 罗超文，李海波，刘亚群.深埋巷道地应力测量及围岩应力分布特征研究[J].岩石力学与工程学报，2010,29(7): 1418-1423.

LUO Chaowen,LI Haibo,LIU Yaqun.Study of distributing characteristics of stress in surrounding rock masses and in-situstress measurement for deeply buried tunnels[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(7): 1418-1423.