理想格上基于身份的代理签名

欧海文 范 祯 蔡斌思 杨明曌

1(北京电子科技学院 北京 100071) 2(西安电子科技大学 陕西 西安 710071)

0 引 言

随着网络的快速发展，为了提高认证的性能，数字签名应运而生。自1976年，Diffie等[1]第一次提出数字签名的概念,到1978年，Rivest等[2]提出基于大整数分解的RSA签名,随后数字签名进入快速发展的阶段，各种基于大整数因子分解和离散对数的数字签名方案被提出。1984年 Shamir[4]提出基于身份的签名IBS(Identity-Based Signature)后，相继出现了很多使用双线性对基于身份的数字签名方案 ，该类签名方案可以将用户的身份等信息作为公钥，对签名的信息进行验证。1996年，Mambo等[3]提出代理签名，该类签名方案中，原始签名者A在不将其私钥给他人的情况下，将其数字签名权利委托给代理签名者B，则B可以代替A进行签名，这样的方案应该满足不可伪造性、可验证性、可区别性等。

但是随着量子计算机和量子算法的出现，人们发现大整数分解和离散对数问题可以在多项式时间内被量子计算机[5]解决，与数论困难问题不同的是格困难问题被认为是可以抵抗量子攻击，而且是后量子密码中最具有潜力的一类，所以构造基于格困难问题的代理签名方案是必不可少的。2012年Micciancio等[6]提出了新的格陷门生成算法，而且将其运用在签名方案中。2014年，Ducas等[7]在文献[6]的前提下，在标准模型下利用理想格提出了一个短的格签名；同年，李明祥等[12]构造了格上基于身份的签名方案。2015年,San等[14]提出可基于理想格的群签名方案, 同年，杨丹婷等[13]提出了理想格上基于身份的签名方案。2016年，孙意如等[15]提出理想格上基于身份的环签名方案。本文利用文献[7]中的理想格特殊的代数结构上的陷门技术，构造了一个基于身份的代理签名方案，使得密钥相对较小，提升了运算效率。

1 预备知识

在本节中，我们给出一些相关的定义和定理。

1.1 格和环

定义1设b1,b2,…,bm是Rn上m个线性无关的向量，则b1,b2,…,bm的所有整系数的线性组合构成的集合称为格，记作：

Λ=L(b1,b2,…,bm)={Σxibi|xi∈Z}

式中：b1,b2,…,bm称作一组格基，m称为格的秩，n称为格的维数。如果定义一个n×m的矩阵Bn×m=(b1,b2,…,bm)，也可以定义该格为Λ=L(B)={Bx|x∈Zm}。如果n=m，称该格为满秩格，一般格和满秩格的性质是一样的。

定义2两种特殊的模q整数格：

Λq(A)={x∈Zm|x=AΤemodq，e∈Zn}

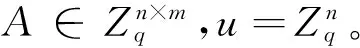
1.2 SIS问题

格上的困难问题有很多种，但这里主要介绍以下困难问题。

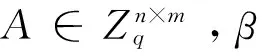
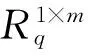
1.3 格上的高斯分布

定义5以c为中心，方差参数是s的n维高斯函数为

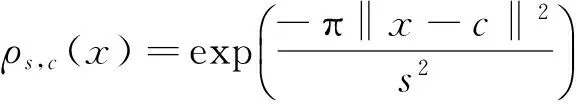
式中：∀x∈n，s∈。

定义6以向量c>0为中心，实参数为s>0可以定义n维格Λ的离散高斯分布为:

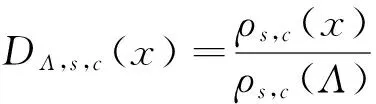
式中，∀x∈Λ。

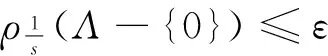
定理1[6]对于任意格Λ(假设是n维格)上的光滑参数都有:

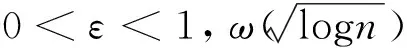
1.4 主要定理和算法

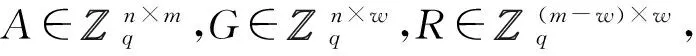
算法1[6]TrapGen(A′,H,s)(陷门生成算法)

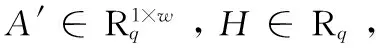
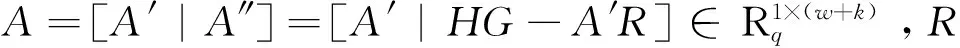
当w≥2logq+2时，A′极大的概率是从均匀分布中选取的，而且A″在统计上也是接近均匀分布。当A′可以随机选取时，算法可以简写为TrapGen(w,H,s)，该算法是随机生成的。

算法2[7]SampleD(A,u,R,s)(原像取样算法)

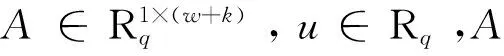
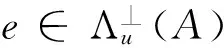
算法3[6]DelTrap(A′=[A|A1],H′,s′) (陷门委托算法)

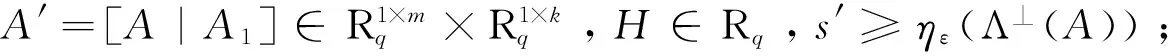
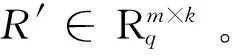
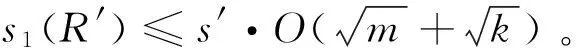
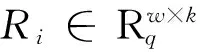
定理3[7]环R上任意一个元素r，都有s1(r)≤‖r‖1=∑|ri|。

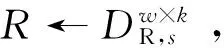
2 签名方案

(1) 主密钥生成

① 运行算法TrapGen(w,I,σ) ，得到随机矩阵A∈R1×m和R∈Rw×k，使得R是A的G-陷门。

② 随机选取矩阵:

A0,A1,…,Al,B0,B1,…,Bd∈R1×k，v∈Rq。

③ 主私钥是R，公布主公钥是:

pk={A,A0,A1,…,Al,B0,B1,…,Bd,v}。

(2) 用户私钥提取

① 利用主公钥和身份信息IDA,IDB，计算

式中：IDA=(a1,a2,…,al),IDB=(b1,b2,…,bl)∈{0,1}l。

(3) 代理授权

① 原始签名者A根据自己的需求生成授权证书W，其中可以包含原始签名人身份信息、代理者的身份信息、代理授权期限、代理授权范围等内容，根据自身需求添加。

② 计算c=H2(IDA,IDB,W)，y=H1(W)。

④ 计算S=xc。

⑤ 将(W,S)公开发布。

(4) 授权验证和代理签名密钥的生成

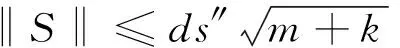
② 如果授权成功，代理者B计算

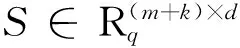
③ 利用代理者B的私钥RB通过添加零行可得到矩阵B′的陷门R′。那么代理签名的密钥为(B′,R′)。

(5) 代理签名

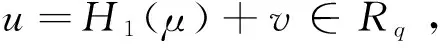
③ 输出(s′,e)即为代理签名。

(6) 验证

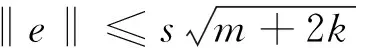
3 方案的分析

3.1 正确性分析

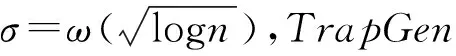
3.2 方案效率分析

本文方案与一般格上代理签名方案的代理授权方式不同，需要用到两个的Hash函数的和一次SampleD算法。代理密钥的生成过程只需要简单的矩阵间的线性运算，不用耗费太多时间。签名阶段进行了一次SampleD算法，计算一次Hash函数，减小了运算复杂度。而且利用了理想格的特殊结构，与同类的其他方案相对比，公私钥的长度相对变短，且签名仅是m+2k维的单个向量，从而提升了运算效率。

3.3 方案安全分析

命题1原始签名者A对代理者B的授权认证不能被伪造。

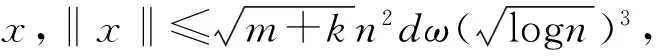
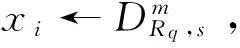
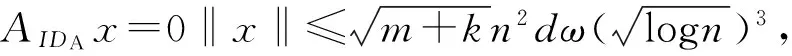
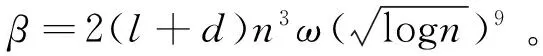
证明假设授权合法的情况下，敌手C可以利用算法D在选择身份和固定选择消息攻击下以不可忽略的概率伪造代理签名，其优势至少是δ。即算法模拟者可以利用C的伪造解决RingSIS问题。

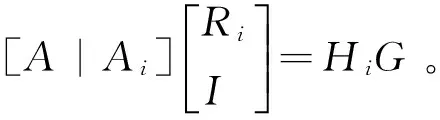
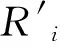
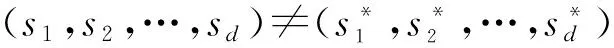
是可逆的。

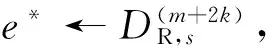
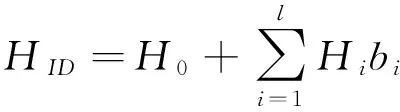
其他代理签名询问：首先进行代理密钥提取询问，将RB*通过添加零行得到B′的陷门R′，再利用其对消息进行签名。

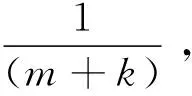
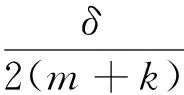
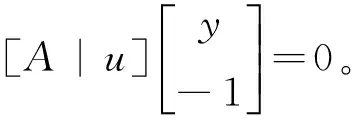
B′*e*=B′*e′=u

A[Im|-RB*|-R′](e′-e*)=0

4 结 语

本文提出了一个基于身份的代理签名方案，与以往的该类签名方案相比，使得授权方式更简单。而且利用了理想格的特点，明显减小了密钥大小，代理签名相对较短，降低了计算复杂度，提升了运算效率。任何人都可以对该代理授权行为进行认证。代理签名的密钥生成既要利用原始签名者A的私钥，还要利用代理者的私钥才能生成，所以防止了原始者伪造和代理签名者的伪造，而且证明了其在选择消息攻击下的强不可伪造性。

[1] Diffie W, Hellman M E. New directions in cryptography[J].IEEE Transactions on Information Theory, 1976,22(6):644-654.

[2] Rivest B R L, Shamir A, Adleman L. A method for obtaining digital signatures and public-key cryptosystems[C]//Communications of the ACM,1978.

[3] Mambo M, Usuda K, Okamoto E. Proxy Signatures: Delegation of the Power to Sign Messages (Special Section on Information Theory and Its Applications)[J].Ieice Transactions on Fundamentals of Electronics Communications & Computer Sciences, 1996, E79-A(9):1338-1354.

[4] Shamir A. Identity-Based Cryptosystems and Signature Schemes[M]//Advances in Cryptology. Springer Berlin Heidelberg, 1984:47-53.

[5] Shor P W. Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer[J]. Siam Journal on Computing, 1996, 41(2):303-332.

[6] Micciancio D, Peikert C. Trapdoors for Lattices: Simpler, Tighter, Faster, Smaller[M]//Advances in Cryptology-EUROCRYPT 2012. Springer Berlin Heidelberg, 2012:700-718.

[7] Ducas L, Micciancio D. Improved Short Lattice Signatures in the Standard Model[M]//Advances in Cryptology-CRYPTO 2014. Springer Berlin Heidelberg, 2014:335-352.

[8] Lyubashevsky V. Lattice signatures without trapdoors[C]//Proceedings of the 31st Annual international conference on Theory and Applications of Cryptographic Techniques. Springer-Verlag, 2012:738-755.

[9] Micciancio D, Regev O. Worst-Case to Average-Case Reductions Based on Gaussian Measures[C]//IEEE Symposium on Foundations of Computer Science. IEEE Computer Society, 2004:372-381.

[10] Lyubashevsky V, Peikert C, Regev O. On Ideal Lattices and Learning with Errors over Rings[J].Journal of the Acm, 2013,60(6):43.

[11] 江明明, 胡予濮, 王保仓,等. 格上的高效代理签名[J]. 北京邮电大学学报, 2014, 37(3):89-92.

[12] 李明祥, 刘阳, 赵秀明. 高效的格上基于身份的签名方案[J]. 计算机应用研究, 2014, 31(3):825-828.

[13] 杨丹婷, 许春根, 徐磊,等. 理想格上基于身份的签名方案[J]. 密码学报, 2015, 2(4):306-316.

[14] Ling S, Nguyen K, Wang H. Group Signatures from Lattices: Simpler, Tighter, Shorter, Ring-Based[C]//Public-Key Cryptography,2015:427-449.

[15] 孙意如, 梁向前, 商玉芳. 理想格上基于身份的环签名方案[J]. 计算机应用, 2016,36(7):1861-1865.