基于出租车轨迹数据的城市热点出行区域挖掘
郑林江 赵 欣 蒋朝辉 邓建国 夏 冬 刘卫宁
1(重庆大学计算机学院 重庆 400030) 2(信息物理社会可信服务计算教育部重点实验室(重庆大学) 重庆 400030) 3(重庆城市综合交通枢纽开发投资有限公司 重庆 401121)
0 引 言
出租车是城市居民日常出行中重要的交通工具之一。区别于公交车和轨道等其他交通出行方式,出租车没有固定的线路和站点,提供了便捷和定制化的个人出行服务。因此,出租车行驶过程中的轨迹信息能够很好地反映城市居民出行特点以及城市交通运行状况,是城市交通分析重要的数据来源[1]。近年来,出租车轨迹数据研究引起了广泛关注,这也促使了诸如路径规划[3-4],基于位置的社交网络[5],智能交通系统[6],以及城市计算[7-9]的快速发展。
根据韦氏词典中的定义,热点区域是指一个比其他区域具有更多的兴趣点、人类活动的地理区域。在现代城市中,城市中的热点区域往往代表着人们出入次数较多、交通流量较大,出行需求较高的区域,是人们频繁、密集出行的直接体现。因此,城市中的热点区域对于城市管理而言具有非常重要的价值。从移动数据中发现城市居民出行热点区域更是成为了一个新的研究关注点。在现有的研究工作中,热点区域发现主要有三种方法,即:传统的问卷调查的方法[10],空间聚类的方法[11-14],以及空间统计分析的方法[15-16]。其中,传统的问卷调查的方法是指通过制作问卷和调查访问的方式收集数据,通过汇总分析,发现人们频繁活动的区域范围。但是,这种方法相对滞后,存在时效性差,准确度低等问题,获得的结果往往参考意义不大。空间聚类的方法隶属于数据挖掘研究领域,该方法通过测算空间数据对象之间的距离从而对输入数据进行分类,探索对象的空间聚集模式。该方法主要是利用数据挖掘中的聚类算法如K-MEANS算法、K-MEDOIDS算法、BIRCH算法、DBSCAN算法等对空间数据进行聚类分析,从而得到空间聚集的点集合,形成密集区域。然而,聚类算法大多采用了数据驱动的计算方法,在处理大规模空间数据时,往往需要更大的计算内存,耗费更长的计算时间,存在着对输入敏感、伸缩性差等缺点。空间统计分析方法是应用统计学方法分析空间单元,通过计算空间单元之间的关联度以及相似性进而发掘热点区域。例如局部空间自相关统计量方法[15]通过测算相邻空间单元之间的相关系数,从而分析它们之间的相关性和相似性,识别不同空间位置的上可能存在的空间聚集模式;空间扫描统计法[16]主要借鉴滑动窗口的思想,通过建立可变大小的滑动窗口对研究区域范围内的数据进行扫描统计,测算区域内所有位置在不同大小的窗口下的最大对数似然比值,进而探测最有可能存在聚集性的区域。空间统计分析方法存在复杂度高、实现难度大和可行性较低等问题,实际情况中并没有得到广泛的应用。
综上所述,为了更好地挖掘城市中的热点区域,提升方法的可伸缩性以及计算效率,受基于密度的聚类算法以及文献[17-20]中区域网格化方法的启发,本文提出了一种基于网格密度的热点区域探测方法:GScan算法。该方法通过划分网格单元将大量空间GPS数据离散化,再利用密度阈值筛选热点网格单元,并对临近可达的热点网格进行合并,从而挖掘出城市中的热点区域。
1 相关定义
首先对相关概念进行定义。
定义1研究区域(Area):给定一个空间数据集合Sd={p1,p2,…,pn},其中,pi(1≤i≤n)代表一个空间数据采样点,那么包含该空间数据集合的区域范围可用式(1)定义如下:
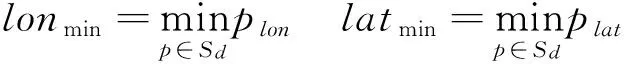
(1)
式中:lonmin、lonmax、latmin、latmax分别代表数据集合中的经纬度的最小值与最大值;相应地,我们定义覆盖全部经纬度位置数据的区域D为:
D=[lonmin,lonmax]×[latmin,latmax]
(2)
定义2网格单元:对于区域D,假设其经度的取值范围为[lonmin,lonmax],纬度的取值范围为[latmin,latmax],对区域D分别从经度以及纬度两个维度对进行划分,把每个属性维的取值范围等分为长度为k的小区间,经过这样的划分,区域D被划分成了若干个k×k大小的正方形单元,由小区间组成的正方形单元被定义为网格单元。图1是我们对重庆市南岸区部分地区以不同的分辨率网格化的结果。
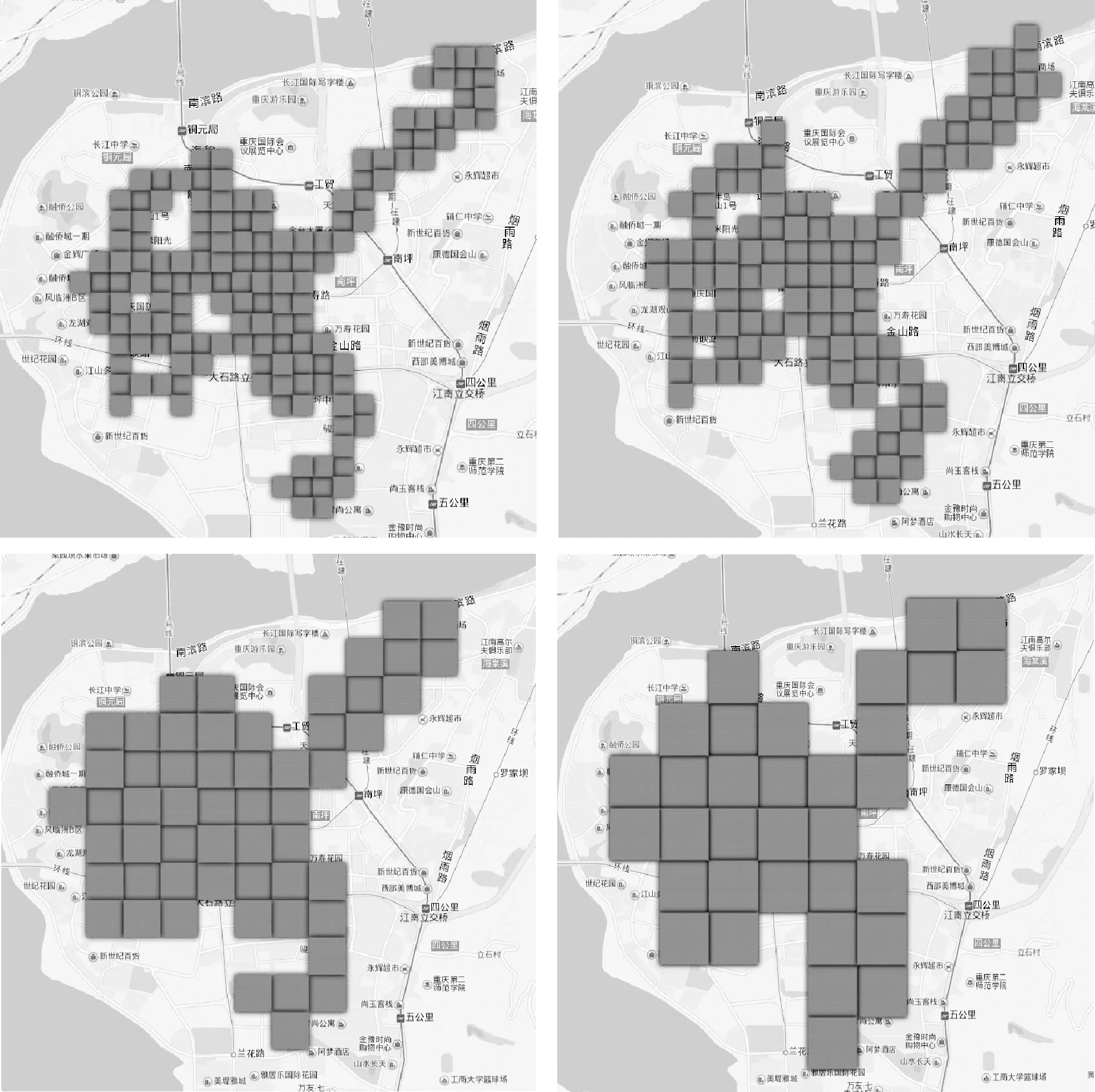
图1 网格化示例
定义3网格单元的数量:对于区域D,由于我们将其划分成了k×k大小的网格单元,所以纬度区间被划分成了m1个小区间,其中m1的计算可用式(3)表示;相应地,经度区间被划分成了m2个小区间,其中m2的计算可用式(4)表示,所以区域网格化后,被划分成的网格单元总个数为两者的乘积,即m=m1×m2。
(3)
(4)
式中:lonmin、lonmax、latmin、latmax分别代表数据集合中的经纬度的最小值与最大值,k为网格单元的大小。
定义4映射关系:对于从属于区域D范围内的空间数据集合Sd,令集合Sd中的一个空间数据点p的经纬度坐标为[lat,lon],则空间数据点p与对应网格单元的所属关系可用公式表示:
(5)
根据数据点与网格单元的所属关系,空间数据点p和网格的映射函数被定义为:
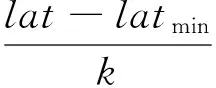
(6)
式中:indlat是网格单元的纬度索引,indlon是网格单元的经度索引,lat和lon分别代表GPS点p的精度和纬度。因此,我们可以用“indlat-indlon”唯一确定一个网格单元。
定义5网格密度:对于网格单元Ui,计算属于该划分网格单元的空间数据点,其空间数据点的总数就叫做网格单元Ui的网格密度,记作den(Ui)。当den(Ui)=0时,称其为空网格单元;当den(Ui)>0时,称其为非空网格单元。
定义6热点网格单元:对于网格单元Ui,如果其网格密度满足:
den(Ui)≥λ
(7)
式中:λ是网格密度阈值,则称网格单元Ui为热点网格单元,否则,称其为普通网格单元。
定义7网格的位置:对于一个网格单元Ui,它的空间位置受其所属空间数据点分布的影响,因此它的位置不能简单的定义为网格单元的中心,为了反映网格中数据点的分布情况,我们定义网格单元的空间位置为经纬度坐标的平均值:
(8)
式中:n是网格单元中空间数据点的数量,lat(pi)和lon(pi)分别代表空间数据点pi的纬度和经度,lat(Ui)和lon(Ui)代表网格单元的位置。
定义8空间距离:在计算空间数据之间的距离时,由于空间数据受高维空间的稀疏性影响,用欧几里德距离计算得到的结果并不能真实反映空间数据之间的距离,为了提高计算准确性,我们定义两个空间数据点之间的距离计算如公式所示:
dis(pA,pB)=Δη×R
(9)
(10)
式中:dis(pA,pB)代表空间数据点pA和pB之间的距离,R代表地球的半径,Δη代表两点与地球中心连线的夹角,ψ和γ分别代表纬度和经度,Δψ和Δγ分别代表两空间数据点纬度和经度之间的差值。
定义9网格直接可达:对于网格集合G,若存在网格单元Ui∈G,网格单元Uj∈G,且满足:
dis(Ui,Uj)≤∂·k
(11)
则我们称网格单元Ui和Uj直接密度可达。其中k为网格单元的大小,∂为距离系数,显然,∂不能太大,以我们的经验,通常取∂∈[1,2],在我们的实验中取∂=1.3。
定义10网格可达:对于网格单元Ui和Uj,如果存在网格序列U1,U2,…,Un-1,Un,使得U1=Ui,Un=Uj,且对1≤r 定义11热点区域:对于网格单元集合G中的一个非空子集H,如果满足: (1) 稠密性:对于∀Ui∈H,其中Ui是一个热点网格单元。 (2) 连通性:对于∀Ui∈H,∀Uj∈H,Ui是从Uj网格密度可达的。 (3) 极大性:对于∀Uj∈H,只要Ui是从Uj网格密度可达的,则存在Ui∈H。 综上所述,若存在满足上述三个条件的网格集合H,则称由网格集合H构成的区域为热点区域。 将研究区域或者数据范围网格化,并用划分生成的网格代替原有的数据集合是一种有效地规约大规模数据的方法。因此,基于网格密度的GScan聚类算法的思想是:首先,对空间数据对象所占的区域进行网格划分,将研究区域范围划分成互不重叠的若干个大小为k×k的正方形网格单元;其次,遍历原有数据集,将原始空间数据通过映射函数映射到所属的网格单元;接着,通过计算所属网格单元中的数据密度,识别网格集合中的热点网格单元,剔除其中的普通网格单元;最后,根据热点网格单元中的数据点的分布计算热点网格单元的位置,并通过计算网格单元间的距离来合并热点网格单元从而得到热点区域。由于原始的空间数据被网格单元所替代,大大规约了所需处理的数据的规模。因此,本文提出的GScan算法具有较好的伸缩性,能够克服基于密度的方法在处理大规模空间数据时存在的不足。 通过第1节的定义可以得知,区别于基于密度的方法,GScan算法处理的最小单位是网格单元,由于网格单元有效地规约了空间数据,减少了数据的规模,所以能够提高计算的速度。接下来,我们将进一步介绍基于网格密度的GScan算法的具体流程。在GScan算法中,需要设定两个参数:k和λ,其中k是网格的大小,而λ是网格密度阈值,对于给定的输入空间数据集合Sd,我们的方法将最终生成热点区域的集合,热点区域集合代表了空间数据的聚集模式。实现GScan轨迹聚类算法主要包括3个阶段: 1) 遍历空间数据集合,确定研究区域范围,并将原始空间数据映射到相应的k×k大小的网格单元。 2) 根据参数λ,筛选出网格单元集合中密度值大于λ的热点网格,并将得到的热点网格集合进行排序。 3) 遍历热点网格集合,对热点网格集合中网格可达的网格单元进行合并,形成热点区域集合。 GScan算法伪代码如下所示: 输入: 空间数据集合Sd={p1,p2,…,pn},网格单元的大小k,网格单元的密度阈值λ 输出: 热点区域的集合O={HA1,HA2,…,HAm} 算法步骤: 1:初始化哈希表HT为空; 2:for each pi∈Sddo 3: 计算得到集合中的最小、最大经纬度值,确定区域范围D; 4:end for 5:for each pi∈Sddo 6: 根据定义4中的映射函数计算其所属网格索引index; 7: if index∈HT then 8: 将pi插入键值index对应的列表; 9: else 10: 以网格索引index为键,将包含数据点pi的列表插入哈希表HT; 11: end if 12:end for 13:初始化热点网格集合G为空; 14:for each k∈HT do 15: if |HT(k)| <λthen 16: continue; 17: else 18: 将其写入集合G; 19: end if 20:end for 21:G <-根据网格密度对集合G进行逆序排序; 22:初始化i等于0,集合O为空; 23:while G≠∅ do 24: 初始化集合HAi; 25: 将集合G中第一个元素等于G1插入HAi,并将其从G中删除; 26: if G≠∅ then 27: for each g∈G do 28: for each h∈HAido 29: if Dis(g,h)<∂.k then 30: 将网格g插入集合HAi; 31: 将网格g从集合G中删除; 32: end if 33: end for 34: end for 35: end if 36: 将HAi插入集合O; 37: i自增1; 38:end while End 在第1阶段(第1行~第12行),首先,算法遍历原始空间数据集合,找到集合中的最大、最小经纬度的值,从而确定区域,接着根据定义4的映射函数,将原始空间数据转化为网格单元。第2阶段(第13行~第21行),遍历网格单元集合,根据参数λ获取集合中的热点网格单元集合,并对热点网格单元进行排序,之所以进行排序,是因为密度大的网格单元之间往往通过密度可达可以生成较大的热点区域,将密度大的网格集中排列有利于减少对集合遍历的次数。第3阶段(第22行~第38行),遍历热点网格集合,并对网格之间网格可达的网格进行合并,形成热点区域集合,算法结束。 GScan算法的总体流程如图2所示。 图2 GScan聚类算法流程图 通过分析GScan算法的执行步骤,我们可以很容易地得出GScan算法的时间复杂度为O(n+m2)。其中,n代表数据集中GPS数据对象的数目,m表示通过划分区域得到的网格单元的个数。GScan算法的时间复杂度是关于数据点数n的线性函数,与m成正比,然而,通常情况下,由于数据点n较大,并且网格单元有效地规约了数据点的数目,总是会有m小于或者远小于n。因此在最差情况下,GScan算法的时间复杂度为O(n+m2),低于DBSCAN算法的时间复杂度O(n2)。 实验中使用的数据集来源于重庆市10 000辆出租车GPS轨迹数据,数据的起始采集时间在2014年8月4日,终止时间在2014年8月17日,为期2周,共14天。其中,车载GPS设备数据采集的时间间隔范围大约为15~20 s,每天每辆车的数据采集的时间涵盖全天24小时,产生的数据量大约在3~5 GB大小(dmp数据格式)。每个数据记录主要包括11个属性,例如车辆的所处的经度、纬度,数据采集时间和车辆载客状态、车牌号、海拔高度、行驶的瞬时速度等信息。 首先,根据出租车载客状态的变化,我们提取了数据中的上车点和下车点数据。具体方法是:将车辆原始轨迹数据按照车辆ID和时间排序,如果数据记录的状态由“空载”状态变成“载客”状态,那么这个轨迹点为上车点。反之,如果数据记录的状态由“载客”状态变成“空载”状态,那么这个轨迹点为下车点。除去噪声数据等无效数据,我们一共从原始数据中提取了上下车数据,图3是我们提取的上下车点数据通过百度地图进行可视化展示的结果。 图3 载客/卸客点数据展示 为了说明GScan算法的有效性,本节特将GScan算法与DBSCAN算法进行了性能对比分析。图4展示了DBSCAN算法和GScan算法在不同规模数据量下运行时间的对比,实验中我们对两种算法设置了相同的参数。从图中可以明显的看到,当数据量大约小于42 000时,DBSCAN算法的运行时间略低于GScan算法,这是因为GScan算法需将原始空间数据集合映射为网格单元,当数据量较小时,数据的分布往往较为稀疏,将数据点转化为网格并没有很好地规约原始数据,相对于DBSCAN算法而言,网格映射便成了额外的步骤消耗了一定的时间。然而,当数据量大于42 000时,随着数据量的增加,GScan算法的运行时间呈现缓慢增长,逐渐体现出可伸缩性,这是因为大量的空间数据被网格单元所替换,替换产生的网格数量远远小于原始数据的数量,有效地减少了原始数据的规模,提高了计算的效率。同时,我们在实验中发现GScan算法的时间消耗主要产生于网格映射阶段,而网格映射阶段可以通过数据划分进而对其进行并行化处理。因此,对于不同规模的数据,我们将原始数据划分为三份对网格映射操作进行并行化,如图4所示,相比为未并行化的GScan算法,并行化后的GScan算法计算速度平均提升了42.48%。 图4 算法性能对比 利用基于网格密度的GScan算法,本节我们对重庆市的时空热点区域进行分析与挖掘。如图5所示,图中展现的是2014年8月4日到2014年8月17日重庆市出租车载客点与卸客点数据随时间的分布情况。通过观察并结合领域知识,我们可以将载客点与卸客点数据按照时间划分为三个部分进行分析:第一个部分是早上7点到早上11点,这个时段通常是人们出门上班的高峰期,乘车需求较大,在交通领域称之为早间出行时段;第二部分是中午12点到下午16点,此时段出行需求分布相对比较均匀,一般称之为午间出行时段;最后一部分是下午17点到晚上23点,此时段与早间出行时段相对应,称之为晚间出行时段,是人们下班回家、参与夜间活动的密集时段。 图5 数据随时间的分布 在对不同时段的热点区域进行分析和挖掘时,我们还需要对GScan算法中的参数进行合理的设置,正如前文理论部分介绍的那样,在GScan算法中主要有网格大小k以及网格密度阈值λ两个参数,以早间出行时段的数据为例,图6展示了设置不同的参数值对计算结果的影响。从图6(a)和(c)中可以看出,对于给定的密度阈值λ,热点区域的数量首先随着网格大小k的增加而增加,当热点区域的数量达到某一最大值之后,随着网格大小k的增加,热点区域的数量逐渐减少。这一现象不难理解,因为当k的值较小时,网格的密度往往难以满足网格密度阈值的约束,因此产生了较少的热点区域;而k值过大时,一些热点区域被合并为更大的热点区域,从而导致了热点区域数量的减少。接着,我们再来看看网格密度阈值λ对结果的影响。从图6(a)和(c)中可以明显的看到,对于给定的网格大小k,较小的λ值产生了较多的热点区域。结合图6(b)和(d)热点区域中数据的累积百分比分布进行进一步分析,我们发现:当λ较小时,GScan算法得到大多是包含较少数据点的热点区域,这些范围较小的热点区域占到了结果总数的85%以上,对于整个城市范围来说,包含数十个点的热点区域显然是不合理的;而当λ增大时,区域内点的数量也逐渐增多,这说明较大的热点区域被生成,并且随着λ的增大热点区域的数量逐渐减少,热点区域的数量的变化的趋势也趋于平稳。例如在图6(a)中,λ=135和λ=150有着相似的走势,我们认为此时计算得到的结果比较稳定,具有较高的参考价值,因此在设置参数时中,我们可以取k=140,λ=135或λ=150。同理,对于卸客点数据而言,可以设置参数k=120,λ=150或λ=160。 图6 参数分析 通过上述参数设置的方法,我们利用GScan算法对早间出行时段、午间出行时段,以及晚间出行时段的出行热点区域进行了挖掘,结果如图7所示。从图中我们明显地可以看到,早间和午间的出行热点区域相对比较集中,数量较少;而晚间的热点区域相对比较分散,数量较多。这点与我们所掌握的常识是吻合的,因为白天人们往往处于工作状态,出行的地点往往集中于城市的大型商圈和住宅区周围,而晚间人们的活动较为丰富,活动的地点选择也较多,所以热点区域的分布也就相对分散。 图7 热点区域 为了进一步分析热点区域的时空分布特点,我们根据重庆市的功能区域特征将热点区域划分为商务区、住宅区、休闲娱乐场所、餐饮购物场所、医疗机构、旅游景点、教育机构、交通枢纽等8个类别。通过结合城市POI数据,我们发现:在早上,出行热点区域主要集中在解放碑-江北嘴-弹子石等中央商务区,观音桥商圈、红旗河沟、两路口等交通枢纽周围,这些区域包含大量的商务区写字楼、居民住宅区以及重要的交通设施,是人们早上出门上班的密集区域。除此之外,我们还注意到在这个时段诸如西南医院等大型医疗机构也是人流量较高的区域。在午间时段,由于时值暑假期间,除了一些中央商务区形成的热点区域之外,南山植物园、三峡博物馆、磁器口古镇、洪崖洞等文化风景区成了出行的热点。同时,相比早间出行时段,杨家坪购物中心、南坪万达广场等一些娱乐购物场所附近的人流量也有了大幅度的增加。而在晚间时段,大型商务区和住宅区再次成为了乘车的热点区域,然而,有所不同的是,龙湖时代天街、北城天街、三峡广场、解放碑步行街等休闲娱乐、餐饮购物集中的场所成为了人们夜间活动的主要区域。 纵观整天热点区域的分布,重庆市的热点区域主要集中在江北国际机场、重庆北火车站、观音桥商圈、南坪商圈、沙坪坝商圈、杨家坪商圈、石桥铺商圈以及两路口交通枢纽等地,这些热点区域在一天中具有较大的人流量,以及较高出行需求,是人们密集出行的直接体现。另一方面,这些热点的分布也从一定程度上反映了重庆市“山城”的地理环境以及以商圈为核心的城市发展策略。 本文基于网格密度的思想提出了一种城市中热点区域的探测方法。该方法通过划分城市网格单元将大量空间数据离散化,相比已有方法,该方法能够有效提升计算的效率和伸缩性。在此基础之上,本文采用真实的出租车轨迹数据进行了实验分析,对方法中的参数设置做了讨论,进一步结合POI数据和时空因素对重庆市人们的出行行为进行了挖掘,实验结果验证了该方法的可行性。需要指出的是,受限于实验数据来源,本文实验仅使用出租车轨迹来分析城市热点区域与居民通勤的时空模式还具有一定的局限性。未来的研究可将各种导航定位终端产生的用户历史轨迹数据、个人情感数据和天气数据相融合更加详尽地分析城市中人们的频繁活动的热点区域。 [1] 齐观德,潘纲,李石坚,等.当出租车轨迹挖掘遇见智能交通[J].中国计算机学会通讯,2013,9(8):30-36. [2] Castro P S,Zhang D,Chen C,et al.From taxi GPS traces to social and community dynamics:A survey[J].ACM Computing Surveys (CSUR),2013,46(2):17. [3] Ziebart B D,Maas A L,Dey A K,et al.Navigate like a cabbie:probabilistic reasoning from observed context-aware behavior[C]//UBICOMP 2008:Ubiquitous Computing,International Conference,Seoul,Korea,September 21-24,2008,Proceedings.DBLP,2008:322-331. [4] Yuan J,Zheng Y,Xie X,et al.T-drive:Enhancing driving directions with taxi drivers’ intelligence[J].IEEE Transactions on Knowledge and Data Engineering,2013,25(1):220-232. [5] 连德富.基于位置社交网络的数据挖掘[D].中国科学技术大学,2014. [6] Yuan W,Deng P,Taleb T,et al.An unlicensed taxi identification model based on big data analysis[J].IEEE Transactions on Intelligent Transportation Systems,2016,17(6):1703-1713. [7] Zheng Y,Liu Y,Yuan J,et al.Urban computing with taxicabs[C]//Proceedings of the 13th international conference on Ubiquitous computing.ACM,2011:89-98. [8] Pan G,Qi G,Wu Z,et al.Land-use classification using taxi GPS traces[J].IEEE Transactions on Intelligent Transportation Systems,2013,14(1):113-123. [9] Zheng Y,Capra L,Wolfson O,et al.Urban Computing:Concepts,Methodologies,and Applications[J].Acm Transactions on Intelligent Systems & Technology,2014,5(3):1-55. [10] 石飞,陆建,王炜,等.居民出行调查抽样率模型[J].交通运输工程学报,2004,4(4):72-75. [11] Zhang M,Liu J,Liu Y,et al.Recommending Pick-up Points for Taxi-drivers Based on Spatio-temporal Clustering[C]//IEEE,International Conference on Cloud and Green Computing.IEEE Computer Society,2012:67-72. [12] Gui Z,Yu H.Mining traffic hot spots from massive taxi trace[J].Journal of Computational Information Systems,2014,10(7):2751-2760. [13] 王亮,胡琨元,库涛,等.随机采样移动轨迹时空热点区域发现及模式挖掘[J].吉林大学学报:工学版,2015(3):913-920. [14] Tang J,Liu F,Wang Y,et al.Uncovering urban human mobility from large scale taxi GPS data[J].Physica A Statistical Mechanics & Its Applications,2015,438:140-153. [15] 王培安,罗卫华,白永平.基于空间自相关和时空扫描统计量的聚集比较分析[J].人文地理,2012(2):119-127. [16] 李小洲,王劲峰.空间扫描统计量方法中候选聚集区域生成的快速算法[J].地球信息科学学报,2013,15(4):505-511. [17] 周勍,秦昆,陈一祥,等.基于数据场的出租车轨迹热点区域探测方法[J].地理与地理信息科学,2016,32(6):51-56. [18] Rong H,Zhou X,Yang C,et al.The Rich and the Poor:A Markov Decision Process Approach to Optimizing Taxi Driver Revenue Efficiency[C]//ACM International on Conference on Information and Knowledge Management.ACM,2016:2329-2334. [19] Chen C,Zhang D,Castro P S,et al.iBOAT:Isolation-Based Online Anomalous Trajectory Detection[J].IEEE Transactions on Intelligent Transportation Systems,2013,14(2):806-818. [20] Yang W,Wang X,Rahimi S M,et al.Recommending Profitable Taxi Travel Routes Based on Big Taxi Trajectories Data[M]//Advances in Knowledge Discovery and Data Mining.Springer International Publishing,2015:370-382.2 基于网格密度的GScan聚类算法
2.1 算法的总体描述
2.2 算法流程
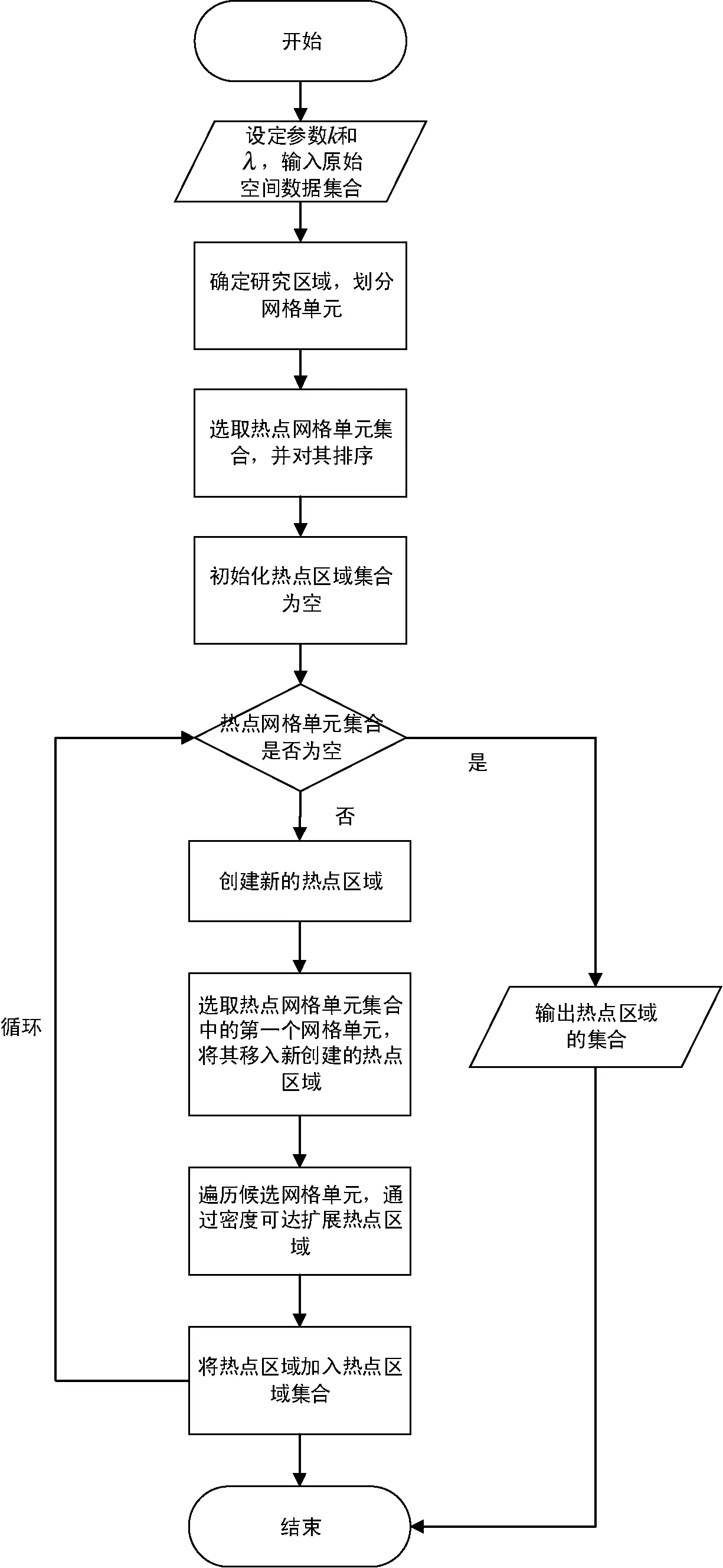
2.3 算法复杂度
3 实验分析
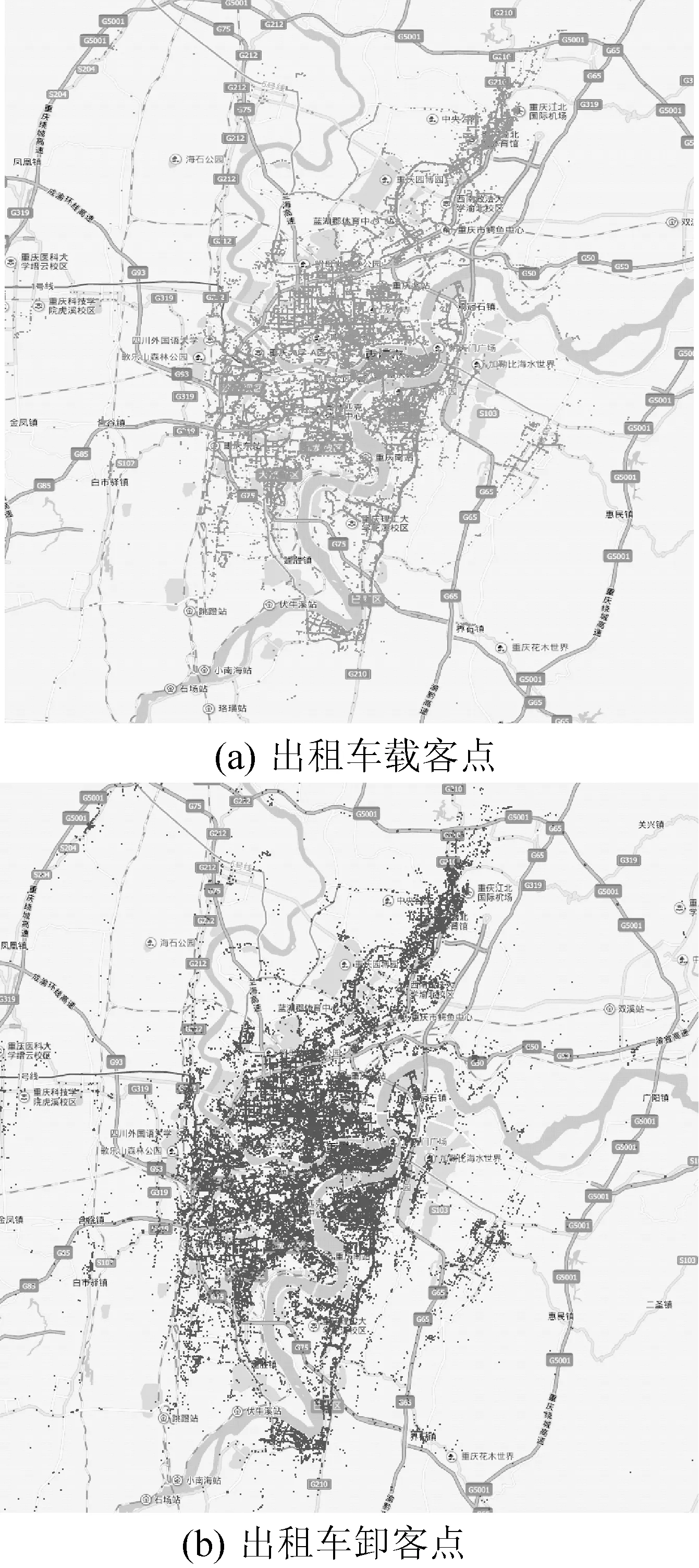
3.1 实验数据
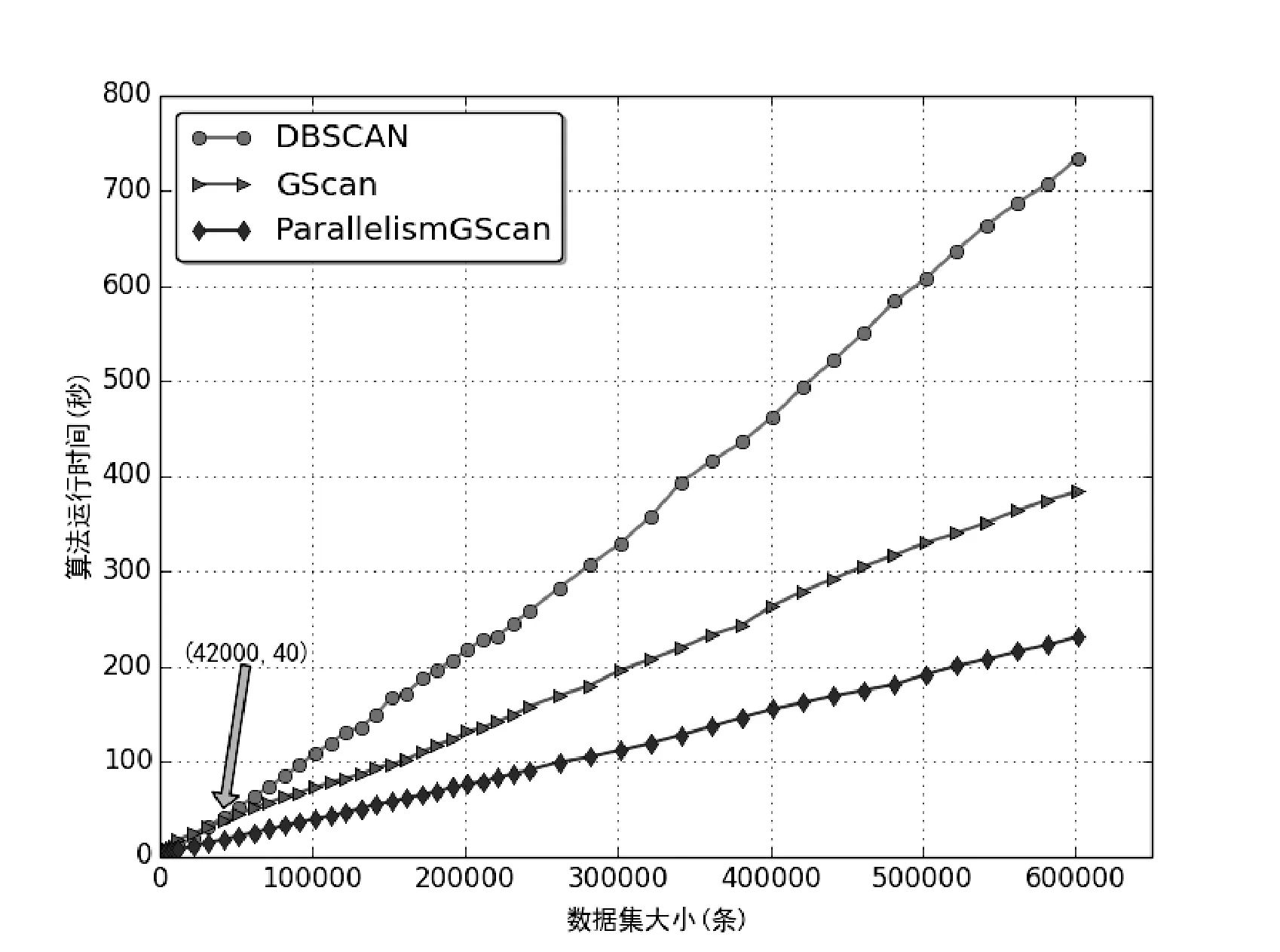
3.2 性能对比实验
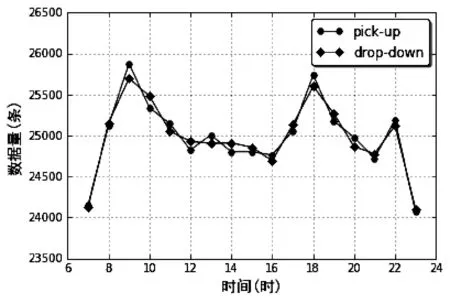
3.3 热点区域挖掘

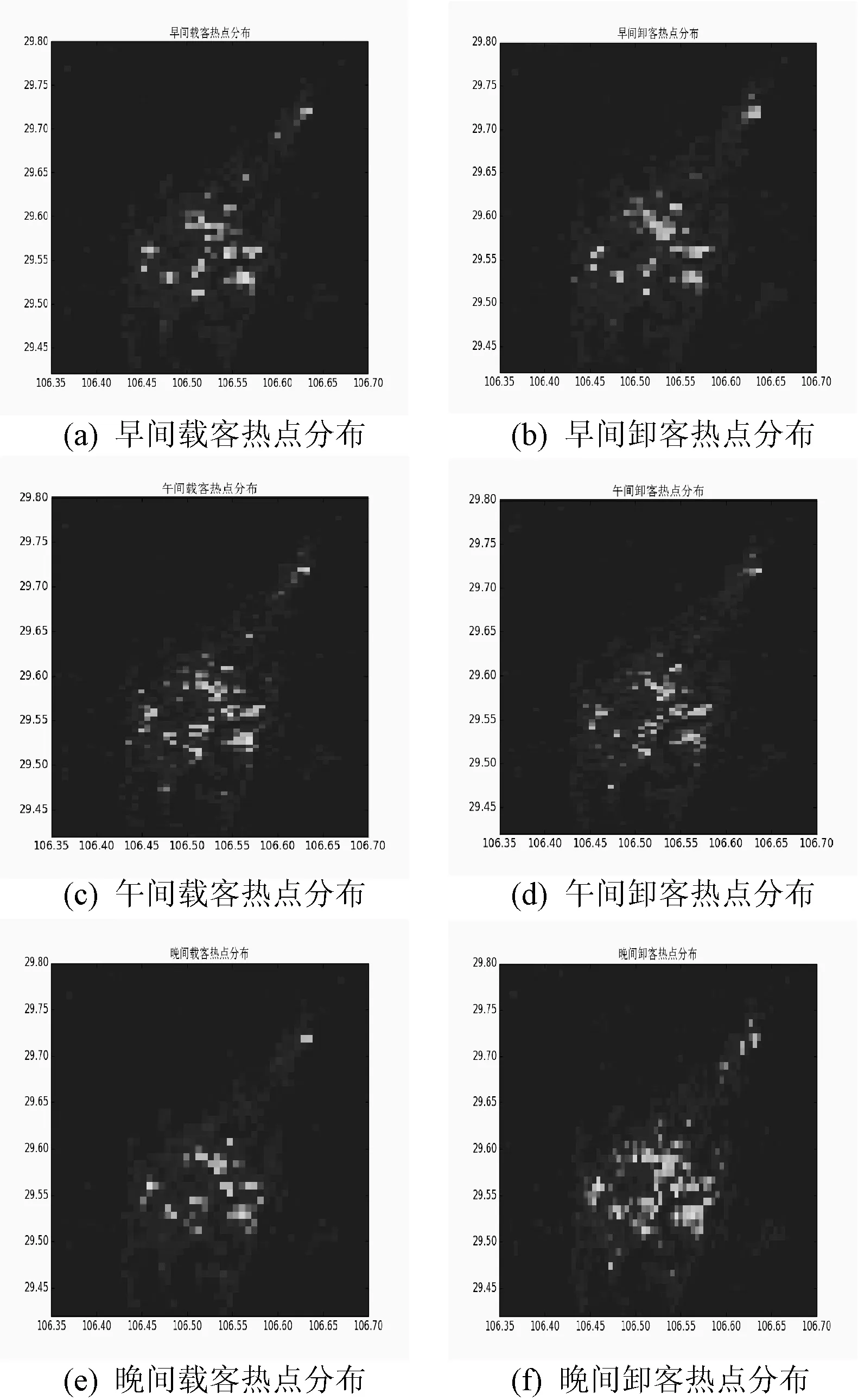
4 结 语

