快速准绝热捷径技术的概况与进展

许剑

摘要

量子計算最基本的操作就是量子态的操作，如何实现高精度、快速和对环境鲁棒性的量子态操作是目前研究的重点。量子绝热过程是一种通过操控含时哈密顿量使得量子系统沿着自身本征态演化的过程，是制备和操控量子态的常用方法。但量子绝热过程需要满足严苛的绝热条件，通常需要较长的操作时间，从而不适用于有较强退相千的环境。为了克服困难，人们提出了量子绝热捷径技术，其中一种方案称为快速准绝热过程，是把绝热条件运用到整个过程中，然后通过调节系统的频率而不是耦合强渡来实现快速的布局数相千转移。本文将概述快速准绝热过程的基本概念及实验进展。

【关键词】量子态操作 布局数相干转移 绝热捷径 快速准绝热

1 前言

近二十年来，信息科学与量子物理相结合，诞生了一门蓬勃发展的交叉学科——量子信息科学，其基础是对量子态实现高保真度的量子操控，例如量子计算中的门操作，量子模拟中的等效磁场，精密测量中对引力常数的测量等等。同时，由于系统不可避免地要和环境耦合，为了减少退相干的影响，也需要对量子态进行尽可能快的操作。

要实现高保真度的量子态操作，最常用的方法称为绝热过程，通过调节脉冲的幅度或者频率对量子态进行操控，由于演化过程仅依赖于系统的几何参数，对系统误差具有很强的鲁棒性。但由于绝热演化需要满足绝热条件，在特定能量尺度下，绝热条件要求绝热过程的操作时间很长。如果系统的退想干效应很强，那么该操作也不能实现高保真度。

因此，寻找能加速操作过程同时不降低甚至增强鲁棒性的操作就称为一个受人关注的热点。例如逆向工程算法、反非绝热场算法以及无跃迁跟随算法等等。这些方法理论上主要都是通过各种方法构造一个额外的哈密顿量来抵消原有哈密顿量中的非绝热效应，实验上主要通过更复杂或更多的参数调控来实现的。但对于一些本身就很复杂的哈密顿量，以上方法在理论和实验上的困难都不小。所以，寻找更简单的加速量子操控的方法就具有了重要的意义。

2 快速准绝热捷径技术

一般的绝热拉曼转移和快速准绝热过程，都需要调节多个系统参数，例如系统中的各个耦合光场的场强，这样多个参数的同时调节为实验带来了很大的困难。这里，我们介绍一种新的相千转移方式，其优点是只需要调节一个系统参数，这样为将来大规模的量子计算提供了一种新的思路。

首先介绍绝热条件，局域的绝热条件要求系统参数的变化率远远小于系统之间的能量差，如下式：其中n和m代表不同的能级，In（t）>和Im（t）>表示对应能级的本征态。满足绝热条件可以保证系统在特定的一个本征态中演化。

具体来说，我们从二能级哈密顿量出发：对应的两个本征态为：

其中可以看出，如果让θ从0演化到π/2，系统保持在|1>态的话，系统将实现从态（0，1）^T到（1，0）^T的转移。

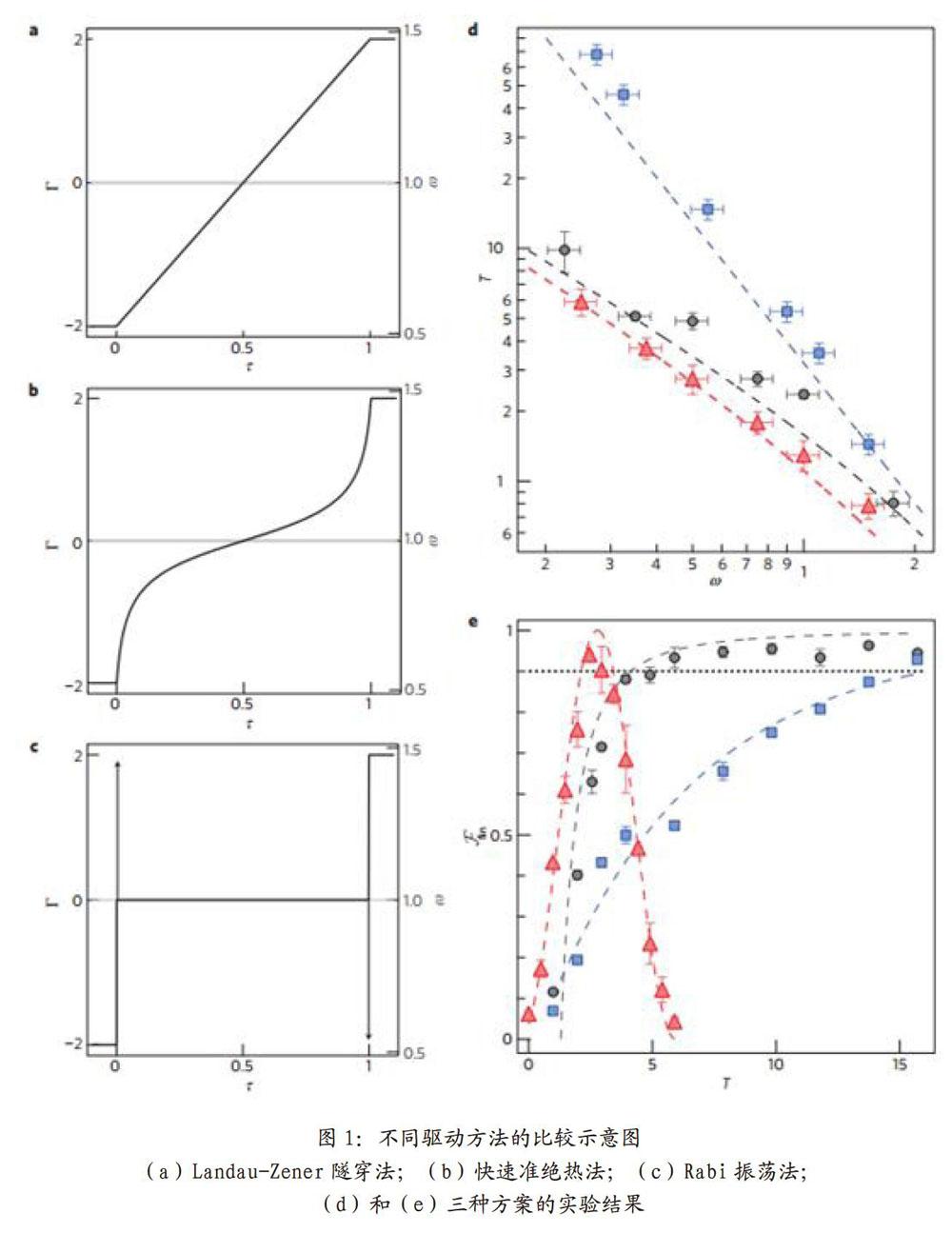
具体让θ演化的方式有很多这里分别介绍如下第一种就是所谓的Landau-Zener隧穿法，让Γ（t）线性地从-Γ变化到Γ，如图1（a）所示，但由于这种方法需要令系统在Γ（t）=0处满足绝热条件，所以整体的演化速率很小;一个改进的方法是把绝热条件运用到演化的整个过程，这就是所谓的快速准绝热过程，换言之能级差大的地方演化速度大，能级小的地方演化速度小，但最小也会满足Γ（t）=0时的情况。具体的理论如下，我们设绝热条件：

然后考虑到公式（2），并运用求导的链式法则，可得：

只要我们求解出公式（5），我们就可以得到在演化每个时刻都满足绝热条件的方案。一种近似求解的方法如图1（b）所示;作为对比，更简单的方法就是让Γ（t）在整个过程中都等于0，这样就是传统的Rabi振荡，这样速度虽然快，但其对参数的变化非常敏感，不利于实现鲁棒性的量子态操作，如图1（c）所示。具体的实验结果如图1（d）（e）所示，可以发现传统的Rabi振荡在鲁棒性上时最差的，快速准绝热过程的鲁棒性最好。

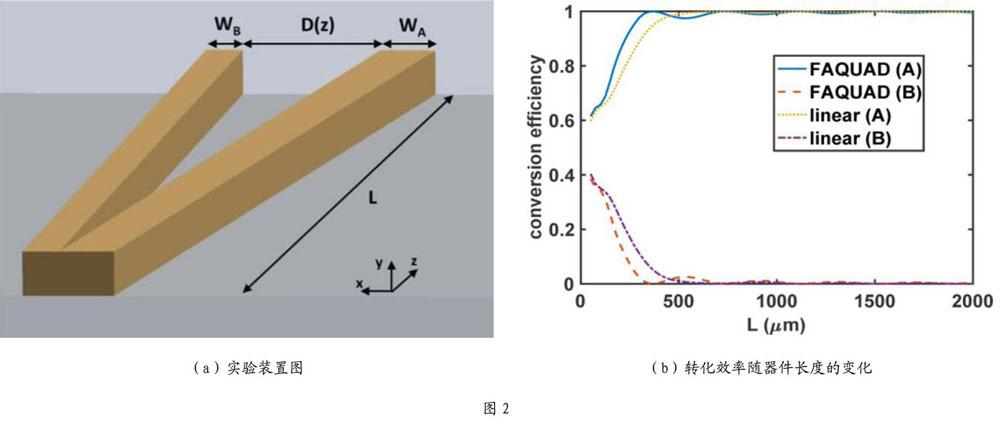
另一种快速准绝热方法是由Martnez-Garaot S.等人提出的对（5）式的严格解，并把这个理论运用到三能级的情况。由于这个方案具有更快的操控速度更好的鲁棒性，所以很快就有实验验证了该方案。具体的实验结果如图2所示。可以看出，运用了快速准绝热技术，可以大大提高系统的性能。

3 总结

当我们能够实现保真度高，速度快和对环境具有鲁棒性的量子态操作，这将为实现量子计算提供最基本和最重要的保证。快速准绝热技术是一种新型的调控量子态的技术。它具有参控的参数少，速度快和鲁棒性强等优点。所以近年来无论在理论上还是在实验上都有很大的发展。展望未来，该方案还存在一些缺点。例如理论上的计算很复杂，这限制了该理论在复杂系统或者多能级系统的应用。这是未来理论上需要进一步研究的地方。

参考文献

[1]杜炎雄，杨金波，吕庆先，颜辉.量子绝热捷径在受激拉曼绝热转移中的应用[J].激光与光电子学进展，2017，54（12）：17-27.

[2]Buluta I，Ashhab S，Nori F.Naturaland artificial atoms for quantumcomputation.Reports on Progress inPhysics，7400），104401（2011）.

[3]Zhu S L，Fu H，Wu C 7，Mang S C，et al..Spin Hall effects for cold atoms ina light-induced gauge potential.Physical Review Letters，97 40401（2006）.

[4]Hu Z K，Sun B L，Duan X C，et al..Demonstration of an ultrahigh-sensitivity atom-interferometryabsolute gravimeter.Physical ReviewA，88（4）：043610（2013）.

[5]Vitanov N.V.，Rangelov A.A.，ShoreB.W.，and Bergmann K.，StimulatedRaman adiabatic passage in physics，chemistry，and beyond，Rev.Mod.Phys.89，015006（2017）.

[6]Torrontegui E，Chen X，Modugno M，Schmidt S，et al..Fast transportof Bose-Einstein condensates.NewJournal of Physics，14 013031（2012）.

[7]Demirplak M，Rice S A.Assistedadiabatic passage revisited.Journalof Physical Chemistry A，109（14）6838（2005）.

[8]Berry M W.Transitionless quantumdriving[J].Journal of Physics A：Mathematical and Theoretical，42（36）365303（2009）.

[9]Landau，L.On the theory of transferof energy at collisions II.Phys.Z.Sow.2 46（1932）.

[10]Zener，C.Non-adiabatic crossing ofenergy levels.Proc.R.Soc.A 137，696（1932）.

[11]Roland，J.&Cerf，N.J.Quantum searchby local adiabatic evolution.Phys.Rev.A 65，042308（2002）.

[12]Mart f nez-Garaot S，Ruschhaupt A，Gillet J，Busch Th，and Muga J.G.，Fast quasiadiabatic dynamics，Phys.Rev.A 92，043406（2015）.

[13]Martnez-Garaot S.，Muga J.G.，and Tseng S-Y.，Short-cuts toadiabaticity in optical waveguidesusing fastquasiadiabatic dynamics，Opt.Express 25，159（2017）.

[14]Chung H.-C.，Lee K.-S.，and TsengS.-Y.，Short and broadband siliconasymmetric Y-junction two-mode（de）multiplexer using fast quasiadiabaticdynamics，Opt.Express 25，13626（2017）.